Effect of Gravitational Field and Temperature Dependent Properties on Two-Temperature Thermoelastic Medium with Voids under G-N Theory

Mohamed I.A.Othman,Magda E.M.Zidan and Mohamed I.M.Hilal

1 Introduction

The generalized thermoelasticity theories have been developed with the aim of removing the paradox of infinite speed of heat propagation inherent in the classical coupled dynamical thermoelasticity theory investigated by Biot(1956).In the generalized theories,the governing equations involve thermal relaxation times and they are of hyperbolic type.The extended thermoelasticity theory by Lord and Shulman(1967)which introduces one relaxation time in the thermoelastic process and the temperature-rate-dependent theory of thermoelasticity by Green and Lindsay(1972)which takes into account two relaxation times are two well established generalized theories of thermoelasticity.Recently,Green and Naghdi(1991,1992 and 1993)developed a generalized theory of thermoelasticity which involves thermal displacement gradient as one of the constitutive variables in contrast to the classical coupled thermoelasticity which includes temperature gradient as one of the constitutive variables.An important feature of this theory is that it does not accommodate dissipation of thermal energy.On this theory the characterization of the material response for a thermal phenomenon is based on three types of the constitutive response functions.The nature of those three types of constitutive response functions is such that when the respective theories are linearized,type I is the same as the classical heat conduction equation(based on Fourier’s law),whereas type II,the internal rate of production of entropy is taken to be identically zero,implying no dissipation of thermal energy.This model is known as the theory of thermoelasticity without energy dissipation.Type III involves the previous two models as special cases,and admits dissipation of energy in general,in this model,introducing the temperature gradient and thermal displacement gradient as the constitutive variables.Chandrasekharaiah(1996a,1996b)solved some problems in thermoelasticity without energy dissipation.Sharma and Chauhan(1999)investigated a problem concerning thermoelastic interactions without energy dissipation due to body forces and heat sources.Othman and Song(2007)have investigated a reflection phenomenon of the plane waves from an elastic solid half-space under hydrostatic initial stress without energy dissipation.Othman et al.(2013a)studied the temperature dependence and the rotation on generalized thermoelasticity with voids under(G-N)theory.

Theory of elastic materials with voids is one of the most important generalizations of the classical theory of elasticity.This theory is concerned with elastic materials consisting of a distribution of small porous(voids)in which the void volume is included among the kinematic variables.Practically,this theory is useful for investigating various types of the geological and the biological materials for which elastic theory is inadequate.A nonlinear theory of elastic material with voids was developed by Nunziato and Cowin(1979).Cowin and Nunziato(1983)developed a theory of linear elastic materials with voids.Puri and Cowin(1985)studied the behavior of the plane waves in a linear elastic material with voids.The domain of influence theorem in the linear theory of elastic materials with voids was discussed by Dhaliwal and Wang(1994).Dhaliwal and Wang(1995)developed a heat flux dependent theory of thermoelasticity with voids.Ciarletta and Scarpetta(1995)discussed some results on thermoelasticity for dielectric materials with voids.Marin in(1997a,1997b)studied uniqueness and domain of influence results in thermoelastic bodies with voids.

The effect of gravity on the wave propagation in an elastic solid medium was first considered by Bromwich in(1898),treating the force of gravity as a type of body force.Sezawa in(1927)studied the dispersion of elastic waves propagated on curved surfaces.In(1965)Love extended the work of Bromwich which investigated the influence of gravity on superficial waves and showed that the Rayleigh wave velocity is affected by the gravity field.Recently Othman et al.(2013b,2013c and 2014)and Othman and Lotfy(2013)have studied many problems using the effect of the gravitational field on thermoelasticity.

Material properties,such as the modulus of elasticity and the thermal conductivity,may be affected by temperature dependent.The temperature dependence of the material properties is neglected when the temperature variation from the initial temperature is low,while the temperature dependence of the material properties is considered when the temperature changes very high.The reactor vessels,turbine engines,space vehicles and refractory industries are affected by high temperature changes.If the temperature dependence of material properties is neglected,this is due to significant errors as discussed by Noda in(1986).Othman and Song in(2008)studied the reflection of the magneto-thermoelastic waves with two relaxation times under the effect of temperature dependent elastic moduli.In(2011)Othman discussed the state-space approach to the generalized thermoelastic problem with the temperature dependent properties and internal heat sources.

The two temperature theory of thermoelasticity proposes that the heat conduction in deformable media depends upon two distinct temperatures,the conducting temperatureθand the thermodynamic temperatureTaccording to Chen and Gurtin in(1968)also Chen and Gurtin(1969)and.While under certain conditions,these two temperatures can be equal,in time independent problems,however,in particular those involving wave propagationθandTare generally distinct according to Warren and Chen in(1973).Youssef in(2006)studied the theory of the two-temperature generalized thermoelasticity.The propagation of harmonic plane waves in the media described by the two-temperature theory of thermoelasticity is investigated by Puri and Jordan in(2006).

The present article is proposed to determine the components of displacement,the stresses,the temperature distribution and the volume fraction field in a homogenous,linear,isotropic,thermoelastic solid with voids in the case of absence and presence of the gravity,the temperature dependent and the two temperature effects.The model was illustrated in the context of(G-N)theory of types II and III.The normalmode analysis isused to obtain the exactexpressions forphysicalquantities.The distributions of considered variables are represented graphically.

2 Formulation of the problem and basic equations

Consider a linear homogeneous isotropic thermoelastic medium with voids and a half-space(y≥0)the rectangular Cartesian coordinate system(x,y,z)having originated on the surfacez=0.For two dimensional problem we assume the dynamic displacement vector as u=(u,v,0).All quantities considered will be a function of the time variablet,and of the coordinatesxandy,the governing equations in the displacement and thermal fields in the absence of body forces and heat sources under the two-temperature generalized thermoelasticity theory as Youssef in(2006).Following Green and Naghdi in(1993),Cowin and Nunziato(1983)the field equations and constitutive relations for a rotating linear homogenous,isotropic generalized thermoelastic solid with voids without body forces,heat sources and extrinsic equilibrated body force under the two-temperature generalized thermoelasticity theory in the context of(G-N)theory of type III,then the basic governing equations of a linear thermoelastic medium with voids under influence of gravitational field and two-temperature will be

The strain-displacement relations

The thermodynamic temperature,Tis related to the conductive temperature,θas

Whereλ,µare the lame’s constants,α,b,ξ1,ω0,m,ψare the material constants due to presence of voids,β=(3λ+2µ)αtsuch thatαtis the coefficient of thermal expansion,ρis the density,Ceis the specific heat,Kis the thermal conductivity,acceleration due to the gravity,dis the two temperature parameter,WhenK∗→0 then(4)reduces to the heat conduction equation in(G-N)theory(of type II).

To investigate the effect of the temperature dependent properties on thermoelastic medium with voids,therefore we assume that

Whereλ0,µ0,β0,α0,ω10,ξ10,ψ0,m0,k0,b0are constants,f(T)is a given nondimensional function of temperature.In the case of a temperature independent modulusofelasticity,f(T)=1,such thatf(T)=(1−α∗T0),whereα∗iscalled the empirical material constant,in the case of the reference temperature independent of modulus of elasticity and thermal conductivityα∗=0.The governing equation can be put into a more convenient form by using the following non-dimensional variables

In terms of non-dimensional quantities defined in equation(9)the governing equations(1)-(4)reduce to(dropping the prime for convenience)

Whereε1,ε2,andε3are the coupling constants.Assuming the scalar potential functionψ1(x,y,t)and the vector potential functionψ2(x,y,t)in dimensionless form

Using equation(15)in equations(10)-(13)to obtain

The components of stress tensor are

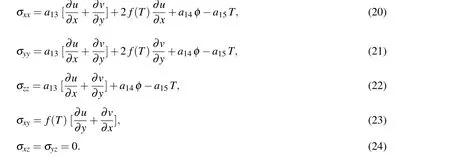
3 Normal mode analysis

The solution of the considered physical quantities can be decomposed in terms of the normal mode as the following form

Using(25)then(16)-(19)take the form

Eliminatingψ∗2,φ∗andT∗between(26)-(29),we obtain the differential equation

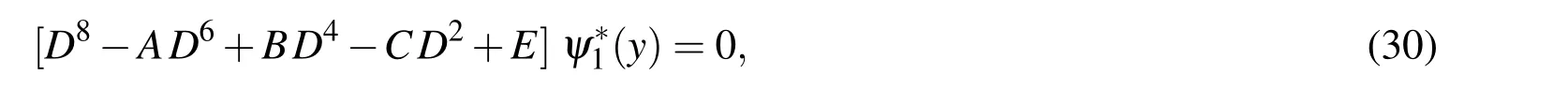
In a similar manner we arrive at

Equation(31)can be factored as

Wherek2n(n=1,2,3,4)are the roots of the characteristic equation of the equation(31).

The general solution of the equation(32),which are bound aty→∞,is given by

SinceRn(n=1,2,3,4)are some coefficients.

To obtain the components of the displacement vector,from(33)and(34)in(14)

From(38),(39),(35)and(37)into(20)-(23)to obtain the components of the stresses

4 Boundary conditions

Consider the boundary conditions to determine the coefficientsRn(n=1,2,3,4),and suppress the positive exponentials to avoid the unbounded solutions at infinity.The coefficientsR1,R2,R3,R4can be defined from the boundary conditions on the surface aty=0.

(1)The mechanical boundary conditions

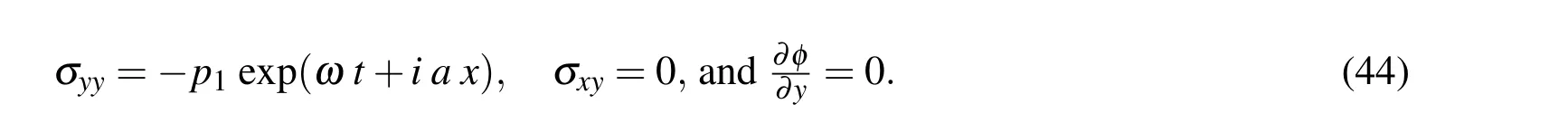
(2)The thermal boundary condition:

The half-space subjected to thermal shock

Wherep1is the magnitude of the applied force in the half-space andp2is the applied constant temperature to the boundary.

Substituting the expressions of the considered variables in the above boundary conditions,to obtain the following equations satisfied by the parameters.

Invoking boundary conditions(44)and(45)at the surfacey=0 of the plate,then obtain a system of four equations,(46)-(49).After applying the inverse of matrix method,one can get the values of the four constantsRn(n=1,2,3,4).

Hence obtain the expressions for the displacement components and the other physical quantities of the plate surface.

5 Numerical results and discussion

In orderto illustrate the obtained theoreticalresultsin the preceding section,following Dhaliwal and Singh in(1980)the magnesium material was chosen for purposes of numerical evaluations.The constants of the problem were taken as

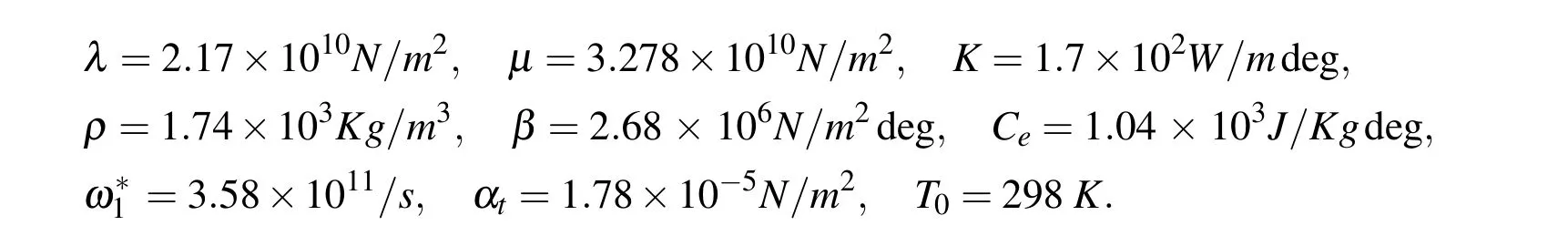
The voids parameters are

The comparisons were carried out for

The above numerical values was used for the distribution of the real parts for the displacement componentsuandv,the temperature distributionθ,the stress componentsσxx,σxyand the change in the volume fraction fieldφwith the distanceyfor(G-N)theory of types II and III,for these cases

(i)In the presence and the absence of the gravity effect in Figs.1-6.

[g=0,9.8with α∗=0.00051and d=0.00015],

(ii)With and without the temperature dependent properties in Figs.7-12.

[α∗=0,0.00051,g=9.8with and d=0.00015],

(iii)With and without the two temperature effect in Figs.13-18.

[d=0.00015,0g=9.8with and α∗=0.00051].

In the graph the solid and dashed lines represent the solutions in the context of the(G-N)theory of type II and the lines with dot represent the derived solutions using(G-N)theory of type III.

Figure 1:The displacement component u distribution against y with and without gravity.

Figure 2:The displacement component v distribution against y with and without gravity.

Figure 3:The distribution of the conductive temperature θ against y with and without gravity.

Figure 4:The distribution of the stress tensor component σxx against y with and without gravity.

Figure 5:The distribution of the stress tensor component σxy against y with and without gravity.

Figure 6:The distribution of the volume fraction field φ against y with and without gravity.

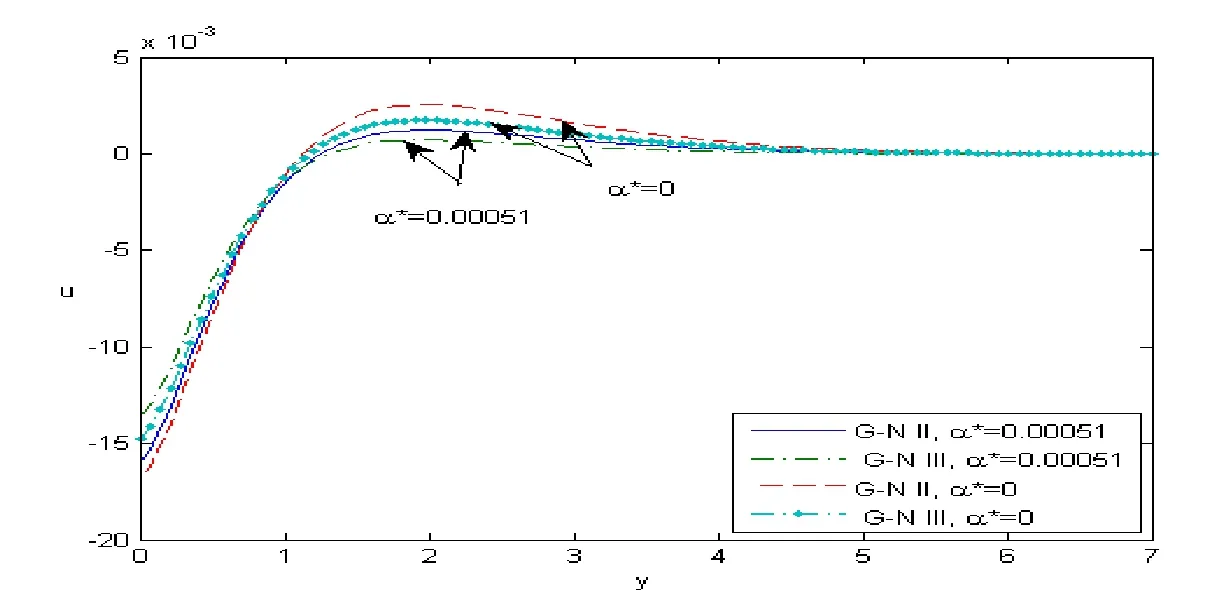
Figure 7:The displacement component u distribution against y with and without temperature dependent.

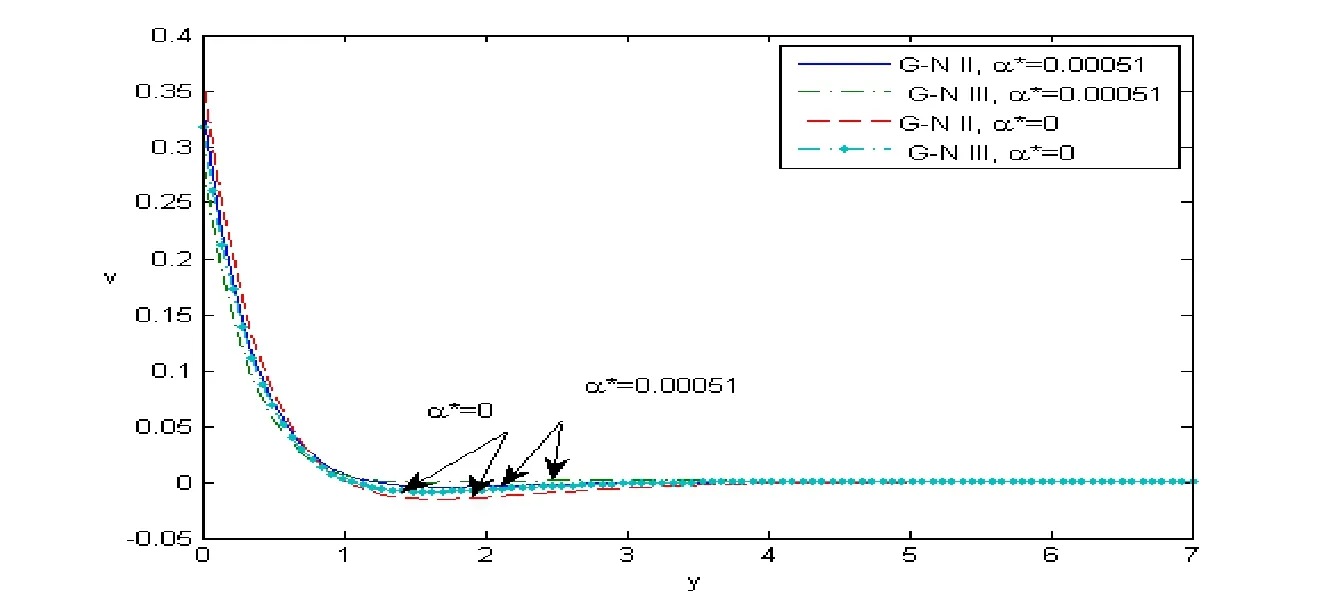
Figure 8:The displacement component v distribution against y with and without temperature dependent.

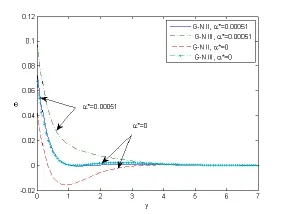
Figure 9:The distribution of the conductive temperature θ against y with and without temperature dependent.

Figure 10:The distribution of the stress tensor σxx against y with and without temperature dependent.

Figure 11:The distribution of the stress tensor σxy against y with and without temperature dependent.

Figure 12:The distribution ofthe volume fraction fieldφ against y with and without temperature dependent.

Fig.1 shows the distribution of the displacementcomponentuin the case ofg=9.8 and g=0,in the context of both types II and III of(G-N)theory;it noticed that the distribution ofuincreased with the increase of the gravity fory＞0,the distribution ofuis directly proportional to the gravity.Fig.2 depicts the distribution of the displacement componentvin the case of g=9.8 and g=0,in the context of both types II and III of(G-N)theory;it noticed that the distribution ofvincreased in 0≤y≤1.3,then decreased in 1.3≤y≤7 with the increase of the gravity value for both types II and III of(G-N)theory.Fig.3 clarifies the distribution of the temperatureθin the case of g=0.9,0 in the context of both types II and III of(G-N)theory;it noticed the distribution ofθdecreased with the increase of the value of the gravity in 0≤y≤7 for both types II and III of(G-N)theory.

Fig.4 depicts the distribution of the stress componentsσxxin the case of g=9.8,0 in the context of both types II and III of(G-N)theory;it noticed the distribution ofσxxdecreased in 0≤y≤0.2 then increased in 0.2≤y≤7 with the increase of the value of the gravity for both types II and III of(G-N)theory.Fig.5 shows the distribution of the stress componentsσxyin the case of g=9.8,0 in the context of both types II and III of(G-N)theory;it noticed the distribution ofσxyincreased in 0≤y≤7 with the increase of the value of the gravity for both types II and III of(G-N)theory.

Fig.6 expresses the distribution of change in the volume fraction fieldφin the context of both types II and III of(G-N)theory in the case of g=9.8,0,it noticed the distribution ofφincreased in 0≤y≤7 for type III of(G-N)theory,while for type II of(G-N)theory the distribution ofφdecreased in 0≤y≤0.05 then increased in 0.05≤y≤7.It explained that all the curves converges to zero,and the gravity has an effective role in the distribution of all physical quantities in this physical problem for both types II and III of(G-N)theory.

Fig.7 depicts the distribution of the displacement componentuin the case ofα∗=0.00051 andα∗=0 in the context of both types II and III of(G-N)theory;it noticed that the distribution ofuincreased in 0≤y≤1 then decreased in 1≤y≤7 with the increase ofα∗for both types II and III of(G-N)theory.Fig.8 shows the distribution of the displacement componentvin the case ofα∗=0.00051 andα∗=0 in the context of both types II and III of(G-N)theory;it noticed that the distribution ofvdecreased in 0≤y≤0.9 then increased in 0.9≤y≤7 with the increase ofα∗for both types II and III of(G-N)theory.

Fig.9 clarifies the distribution of the temperatureθin the case ofα∗=0.00051,0 in the context of both types II and III of(G-N)theory;it noticed the distribution ofθincreased with the increase of the value ofα∗in 0≤y≤7 for both types II and III of(G-N)theory.

Fig.10 depicts the distribution of the stress componentsσxxin the case ofα∗=0.00051,0 in the context of both types II and III of(G-N)theory;it noticed the distribution ofσxxdecreased in 0≤y≤7 with the increase of the value ofα∗for both types II and III of(G-N)theory.Fig.11 shows the distribution of the stress componentsσxyin the case ofα∗=0.00051,0 in the context of both types II and III of(G-N)theory;it noticed the distribution ofσxydecreased in 0≤y≤2.3 then increased in 2.3≤y≤7 with the increase of the value ofα∗for both types II and III of(G-N)theory.

Fig.12 expresses the distribution of change in the volume fraction fieldφin the context of both types II and III of(G-N)theory in the case ofα∗=0.00051,0,it noticed the distribution ofφdecreased in 0≤y≤7 with the increase of the value ofα∗for both types II and III of(G-N)theory.It explained that all the curves converges to zero,and the temperature dependent properties have an effective role in the distribution of all physical quantities in this problem for both types II and III of(G-N)theory.

Fig.13 depicts the distribution of the displacement componentuin the case of d=0.00015 and d=0 in the context of both types II and III of(G-N)theory;it noticed that the distribution ofuincreased in 0≤y≤7 for(G-N)theory of both types II and III with the increase of the two-temperature parameter d.

Fig.14 shows the distribution of the displacement componentvin the case of d=0.00015 and d=0 in the context of both types II and III of(G-N)theory;it noticed that the distribution ofvincreased in 0≤y≤7 for(G-N)theory of both types II and III with the increase of the two-temperature parameter d.

Fig.15 clarifies the distribution of the temperatureθin the case of d=0.00015,0 in the context of both types II and III of(G-N)theory;it noticed the distribution ofθdecreased with the increase of the value of d in 0≤y≤7 for type II of(G-N)theory,while the distribution ofθincreased with the increase of the value of d in 0≤y≤7 for(G-N)theory of type III.

Fig. 16 depicts the distribution of the stress componentsσxxin the case of d=0.00015,0 in the context of both types II and III of(G-N)theory;it noticed the distribution ofσxxdecreased in 0≤y≤7 with the increase of the value of d for type III of(G-N)theory,but the distribution ofσxxincreased in 0≤y≤7 with the increase of the value of d for(G-N)theory of type II.

Fig. 17 shows the distribution of the stress componentsσxyin the case of d=0.00015,0 in the context of both types II and III of(G-N)theory;it noticed the distribution ofσxyfor(G-N)theory of both types II and III decreased in 0≤y≤7 with the increase of the value of d.

Fig.18 expresses the distribution of change in the volume fraction fieldφin the context of both types II and III of(G-N)theory in the case of d=0.00015,0 it noticed the distribution ofφincreased in 0≤y≤7 with the increase of the value of d for type II of(G-N)theory,while the distribution ofφfor type III of(G-N)theory increased in 0≤y≤0.05 then decreased in 0.05≤y≤7 with the increase of the value of d.It explained that all the curves converges to zero,and the twotemperature effect has an effective role in the distribution of all physical quantities in this problem for both types II and III of(G-N)theory.

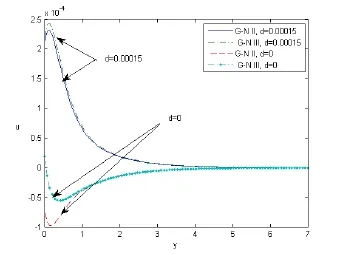
Figure 13:The displacement component u distribution against y with and without two temperature.

Figure 14:The displacement component v distribution against y with and without two temperature.

Figure 15:The distribution of the conductive temperature θ against y with and without two temperature.

Figure 16:The distribution of the stress tensor component σxx against y with and without two temperature.

Figure 17:The distribution of the stress tensor component σxy against y with and without two temperature.

Figure 18:The distribution ofthe volume fraction fieldφ against y with and without two temperature.

6 Conclusion

In this article,we have studied the effect of the gravitational field and temperature dependent properties due to two-temperature for thermoelastic medium with voids.The analysis of the components of displacement,the stresses,the temperature distributions and the change in the volume fraction field due to the gravity,the temperature dependent properties,and the two-temperature effect for thermoelastic medium with voids is an interesting problem of thermo-mechanical.The gravitational influence,the temperature dependent properties and the two-temperature effect are significant in the current model since the amplitudes of these quantities are varying(increasing or decreasing)under the effect of the used fields.The nor-mal mode analysis technique has been used which is applicable to a wide range of problems in thermoelasticity.The value of all physical quantities converges to zero with an increase in the distanceyand all functions are continuous.Finally it deduced that the deformation of a body depends on the nature of the applied forces and thermal effects as well as the type of boundary conditions.

Biot,M.A.(1956):Thermoelasticity and irreversible thermodynamics.Journal of Applied Physics,vol.7,pp.240-253.

Bromwich,T.J.(1898):On the influence of gravity on elastic waves and in particular on the vibrations of an elastic globe.The Proceedings of the London Mathematical Society,vol.30,pp.98-120.

Chandrasekharaiah,D.S.(1996a):Thermoelastic plane waves without energy dissipation.Mechanics Research Communications,vol.23,pp.549-555.

Chandrasekharaiah,D.S.(1996b):One-dimensionalwave propagation in the linear theory of thermoelasticity with energy dissipation.Journal of Thermal Stresses,vol.19,pp.695-710.

Chen,P.J.;Gurtin,M.E.(1968):On a theory of heat conduction involving twotemperatures.Journal of Applied Mathematics and Physics,vol.19,pp.614-627.

Chen,P.J.;Gurtin,M.E.;Williams,W.O.(1969):On the thermodynamics of non simple elastic materials with two-temperatures.Journal of Applied Mathematics and Physics,vol.20,pp.107-112.

Ciarletta,M.;Scarpetta,E.(1995):Some results on thermoelasticity for dielectric materials with voids.Journal of Applied Mathematics and Mechanics,vol.75,pp.707-714.

Cowin,S.C.;Nunziato,J.W.(1983):Linear theory of elastic materials with voids.Journal of Elasticity,vol.13,pp.125-147.

Dhaliwal,R.S.;Singh,A.(1980):Dynamic coupled thermoelasticity.Hindustan Publishing Corporation,New Delhi.

Dhaliwal,R.S.;Wang,J.(1994):Domain of influence theorem in the theory of elastic materials with voids.International Journal of Engineering Science,vol.32,pp.1823-1828.

Dhaliwal,R.S.;Wang,J.(1995):A heat-flux dependent theory of thermoelasticity with voids.Acta Mechanica,vol.110,pp.33-39.

Green,A.E.;Lindsay,K.A.(1972):Thermoelasticity.Journal of Elasticity,vol.2,pp.1-7.

Green,A.E.;Naghdi,P.M.(1991):A re-examination of the basic postulates of thermo-mechanics.Proc Royal Society London Avol.432,pp.171-194.

Green,A.E.;Naghdi,P.M.(1992):On undamped heat wave in elastic solids.Journal of Thermal Stresses,vol.15,pp.253-264.

Green,A.E.;Naghdi,P.M.(1993):Thermoelasticity without energy dissipation.Journal of Elasticity,vol.31,pp.189-209.

Lord,H.W.;Shulman,Y.A.(1967):Generalized dynamical theory of thermoelasticity.Journal of the Mechanics and Physics of Solids,vol.15,pp.299-309.

Love,A.E.H.(1965):Some problems of geodynamics.Cambridge University Press,London.

Marin,M.(1997a):A uniqueness result for body with voids in linear thermoelasticity.Rendiconti di Matematica,vol.17,pp.103-113.

Marin,M.(1997b):On the domain of influence in thermoelasticity of bodies with voids.Archiv der Mathematik,vol.33,pp.301-308.

Noda,N.(1986):Thermal stresses in materials with temperature-dependent properties.in Hetnarski R.B.(Ed.).Thermal stresses I,North-Holland,Amsterdam.

Nunziato,J.W.;Cowin,S.C.(1979):A non-linear theory of elastic materials with voids.Archive for Rational Mechanics and Analysis,vol.72,pp.175-201.

Othman,M.I.A.;Song,Y.(2007):Reflection of plane waves from an elastic solid half-space under hydrostatic initial stress without energy dissipation.International Journal of Solids and Structures,vol.44,pp.5651-5664.

Othman,M.I.A.;Song,Y.(2008):Reflection of magneto-thermoelastic waves with two relaxation timesand temperature dependentelastic moduli.AppliedMathematical Modelling,vol.32,pp.83-500.

Othman,M.I.A.(2011):State-space approach to the generalized thermoelastic problem with temperature-dependent elastic moduli and internal heat sources.Journal of Applied Mechanics and Technical Physics,vol.52,pp.644-656.

Othman,M.I.A.;Zidan,M.E.M.;Hilal,M.I.M.(2013a):Effect of rotation on thermoelastic material with voids and temperature dependent properties of type III.Journal of Thermoelasticity,vol.1,pp.111.

Othman,M.I.A.;Atwa,S.Y.;Jahangir,A.;Khan,A.(2013b):Generalized magneto-thermo-microstretch elastic solid under gravitational effect with energy dissipation.Multidiscipline Modeling in Materials and Structures,vol.9,pp.145-176.

Othman,M.I.A.;Lotfy,Kh.(2013):The effect of magnetic field and rotation on 2-D problem of a fiber-reinforced thermoelastic using three models with influence of gravity.Mechanics of Materials,vol.60,pp.120-143.

Othman,M.I.A.;Zidan,M.E.M.;Hilal,M.I.M.(2013c):The influence of gravitational field and rotation on thermoelastic solid with voids under Green-Naghdi theory.Journal of Physics,vol.2,pp.22-34.

Othman,M.I.A.;Abo-Dahab,S.M.;Lotfy,Kh.(2014):Gravitational effect and initial stress on generalized magneto-thermo-microstretch elastic solid for different theories.

Applied Mathematics and Computation,vol.230,pp.597-615.

Puri,P.;Cowin,S.C.(1985):Plane waves in linear elastic materials with voids.Journal of Elasticity,vol.15,pp.167-183.

Puri,P.;Jordan,P.M.(2006):On the propagation of harmonic plane waves under the two-temperature theory.International Journal of Engineering Science,vol.44,pp.1113-1126.

Sezawa,K.(1927):Dispersion of elastic waves propagated on the surface of stratified bodies and on curved surfaces.Bulletin of the Earthquake Research Institute University of Tokyo,vol.3,pp.1-18.

Sharma,J.N.;Chouhan,R.N.(1999):On the problems of body forces and heat sources in thermoelasticity without energy dissipation.Indian Journal of Pure and Applied Mathematics,vol.30,pp.595-610.

Warren,W.E.;Chen,P.J.(1973):Wave propagation in the two-temperature theory of thermoelasticity.Acta Mechanica,vol.16,pp.21-33.

Youssef,H.M.(2006):Theory of two-temperature generalized thermoelasticity.IMA,Journal ofApplied Mathematics,vol.71,pp.383-390.

Appendix