基于模板的电能质量信号数据压缩＊

崔 旭 尹为民 王黎明

（海军工程大学电气与信息工程学院 武汉 430033）

0 引 言

对于现代电力系统，发生故障是不可避免.为了能够采集到电力系统故障或异常发生时的电能质量扰动信号，须在较短的时间内采集到大量的数据，因而在电能质量扰动信号传输存储过程中需要一种高效的压缩方法，在压缩过程中保持扰动信号的主要特征不丢失，以便进行扰动原因分析和扰动识别等，并使压缩后的数据量尽可能少［1］.因为小波变换是空间（时间）和频率特性，采用小波变换的数据压缩技术非常适合对电能质量信号进行压缩［2－6］.Ö.N.Gerek等［7］提出了电能质量信号的二维分析与压缩的思想，在此基础上高培生等［8］利用二维小波变换与嵌入零树小波编码算法对电能质量信号取得成功，张明等［9］利用JPEG2000同样取得了比较好的压缩效果.

虽然上述二维压缩算法应用于电能质量信号压缩都取得了比较好的效果，但是其核心思想是将电能质量信号转换为二维图像并利用图像压缩系列算法进行压缩［10－12］.因为电能质量信号转化的二维图像有其不同于自然图像的自身特点，所以单纯将图像压缩算法移植到电能质量压缩领域并不能达到最好的压缩效果.为充分利用二维电能质量信号特点，文中在二维提升小波变换与SPIHT编码算法基础上提出了一种基于模板的编 码 算 法 （template－based SPIHT compression algorithm，以下简称TB－SPIHT算法），其优良的压缩性能在实验中得到了验证.

1 提升小波变换

二维离散小波变换最有效的实现方法之一是采用Mallat算法，但是此算法计算量大，复杂度高，不利于硬件实现，提升小波有效解决了这些问题.提升方法进行小波变换可以分为以下3个阶段：分解、预测和更新［13－15］.

1）分解 即由信号的奇偶性将原始信号si分解为2个较小的偶信号序列si－1和奇信号序列di－1，即si－1＝s2n，di－1＝s2n＋1（n＝1，2，3…）.

2）预测 即在原始信号相关性的基础上用si－1来预测di－1，用预测误差δ＝di－1－P（si－1）来代替di－1.其中P为预测算子.

3）更新 即通过di－1来更新si－1，亦即用ξ＝si－1＋U（di－1）来代替si－1，其中：U 为更新算子.

重构过程是分解过程的逆过程，包括反更新、反预测和合并，不再赘述.由此，可给出基于提升的正向小波变换和逆向小波变换的流程，见图1，2.

图1 提升的正向小波变换流程图

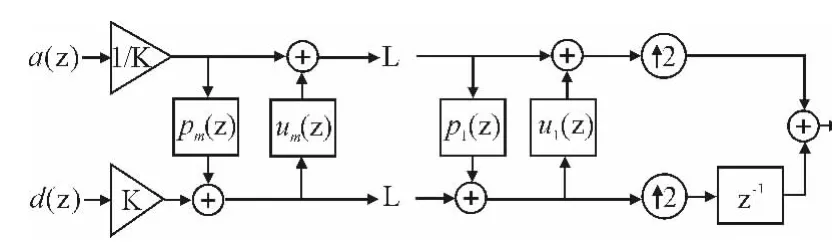
图2 提升的逆向小波变换流程图

2 电能质量数据的模板性分析

电能质量信号是一种准周期信号，其波形呈现某种相似性，因而是一种冗余度较大、而信息熵较小的信号，从理论上来讲，应该具有较大的压缩比.将一维电能质量信号按周期分段，逐列排列，这样原周期之间的相似性映射到二维图像相邻列之间的相似性，一周期内部采样点之间的变化趋势映射到二维图像一行之中.已有的电能质量二维压缩算法在信号二维化之后直接应用二维图像的相关压缩算法对其压缩，但是电能质量信号转换成的二维信号并不是传统意义上承载视觉信息的图片，其各像素点分布更有规律性，所以文中提出了一种适合电能质量二维信号的压缩算法.

因为标准的电能质量信号为频率50Hz，幅值380V的三项正弦信号.现对单独一项进行采样，设每次采样一周期共256个点，采样256周期.对于标准电能质量信号采样数据按照上述排列方式进行维度变换，当没有任何噪声及扰动的情况下，二维图像的同一行的数据应全部相同.见图3，x（p，n）为第p个周波的第n个相位点电压值.将此信号称为电能质量信号基本模板.

图3 电能质量信号模板

对于工程中的电能质量信号，当没有发生故障时，可以认为同一周期对应点采样值与标准信号基本相同，不同之处在于实际信号可能存在一定的噪声.但是如发生故障，根据前文所述的采样信号二维转换方法，故障周期对应的采样点一定会分布于二维信号的某几列，见图4.图中突出部分为加入3，5，7，9次谐波的电能质量信号.

图4 含噪声谐波的电能质量二维信号

基于提升小波理论，对图像中的一块数据进行行变换或列变换后，图像块的相对位置并不会发生改变.根据此理论，图4信号小波变换后的小波域系数大部分都与模板的小波域系数相同.图5为待压缩信号与模板小波变换后LL3，HL3，LH3，HH3部分的小波系数的差值（3层提升小波变换，小波基选用9／7小波）.

图5 信号小波系数与模板小波系数差

根据香农的信息论相关理论，可以认为图5是图4信号所携带的真正信息.因为电能质量信号的模板性，如直接应用图像压缩算法则造成了大量的编码位编码已知的模板信息.

3 TB－SPIHT算法

由上节分析可知，电能质量信号具有模板性这一特点.为解决电能质量信号中存在大量模板性的冗余信息这一问题文中提出了TB－SPIHT算法.TB－SPIHT算法的具体过程如图6所示.下面将详细介绍TB－SPIHT的算法步骤.

图6 TB－SPIHT算法流程

3.1 空间方向树

TB－SPIHT算法是在SPIHT算法（set partitioning in hierarchical trees）基础上改进而成.在对图像进行二维小波变换之后，各子带之间的数据可以看成是一个树状的结构（见图7），各子带之间的箭头表示各频带之间的父－子依赖关系，其大致反映了相同空域中同方向子带的性能.算法中通过将小波系数与给定阈值T进行比较来确定是否编码传输.

图7 小波树结构

3.2 分集排序规则

首先引入下面4个集合符号与3个有序表.

集合符号 （1）O（i.j）为节点（i.j）所有孩子的集合；（2）D（i.j）为节点（i.j）所有子孙的集合（包括孩子）；（3）L（i.j）为节点（i.j）所有非直系子孙的集合（不包括孩子），其中L（i.j）＝D（i.j）－O（i.j））；（4）H 为所有树根的坐标集.

SPIHT算法引入了3个有序表来存放重要信息 （1）LSP为重要系数表；（2）LIP为不重要系数表；（3）LIS为不重要子集表.

这3个表中，每个表项都使用坐标（i.j）来标识.在LIP和LSP中，坐标（i.j）表示单个小波系数；而 LIS中，坐标（i.j）代表2种系数集，即D（i.j）或L（i.j），分别称为 D型表项、L型表项.

SPIHT算法的分集规则如下：（1）初始坐标集为｛（i.j）｜（i.j）∈H｝，｛D（i.j）｜（i.j）∈H｝；（2）若D（i.j）关于当前阈值是重要的，则D（i.j）分裂成L（i.j）和O（i.j）；（3）若L（i.j）关于当前阈值是重要的，则L（i.j）分裂成4个集合D（lO，mO），（lO，mO）∈O（i.j）.

对于集合中的小波系数，采用式（1）进行重要性测

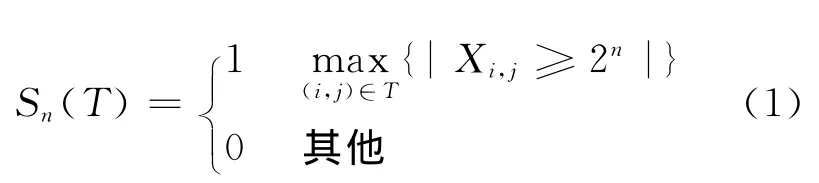
式中：阈值n为

3.3 SPIHT算法的编码过程如下

1）初始化

（1）初始化模板信息 将模板幅值、频率、相位作为头文件传输.

（2）更新压缩域X（i，j）＝X（i，j）－B（i，j）.式中：B（i，j）为模板小波变换域系数.

（3）初始化编码信息

阈值T 的指数n＝［lb（max｜X（i，j）｜）］

LSPØ

LIP＝｛（i.j）｜（i.j）∈H｝

LIS＝｛D（i.j）｜（i.j）∈H 且（i.j）具有非零子孙｝

2）排序扫描

（1）对LIP的每个记录（i.j）作

a.输出Sn（i.j）.

b.如果Sn（i.j）；＝1，将（i.j）移入LSP，并输出 Xi，j的符号位.

（2）对LIS的每个记录（i.j）作

a.如果这个记录是D（i.j）类

a）输出Sn（D（i.j））.

b）如果Sn（D（i.j））＝1则

① 对每一个（l，m）∈O（i.j）作输出Sn（l，m）；如果Sn（l，m）＝1，将（l，m）加入到LSP，并输出 Xl，m的符号位.

② 如果L（i.j）不为空集，将（i.j）加入到LIS尾部，并标明 L 类集合，转到（2.2.2），如果L（i.j）是空集合，将（i.j）从LIS移除.

b.如果记录为L（i.j）类集合，则

a）输出Sn（L（i.j））.

b）如果Sn（L（i.j））＝1则将每个（l，m）∈O（i.j）加入到LIS尾部，并标记为D型表项；从LIS中移除（i.j）项.

3）对 LSP中每一项（i.j），输出 Xi，j的第n个最高有效值.

4）n＝n－1，返回步骤3）.

解码过程为编码过程的逆向运算，对此不在赘述.

4 实验结果

为提高电网采集数据的压缩品质，文中采用输入电压范围±380V，16位采样数据，具有低采样噪声的电网数据同步采集装置，每周波256个采样点，共采集256个周波，其中第200～230个采样周期发生电能质量故障，信号变为加入3，5，7，9次谐波的故障信号.二维化后的波形（见图4），x（p，n）为第p个周波的第n个相位点电压值.将电压波形沿相位点去除均值后，见图8，可以看出数据噪声幅值在0.04V以内.

图8 去均值后噪声

对实验信号进行5层提升小波分解，小波基采用9／7小波，对小波系数分别采用SPIHT编码方式与TB－SPIHT编码方式进行编码.采用SPIHT的编码循环次数作为变量参数（进行一次分裂扫描与一次精细扫描记为一个循环）.将CR（压缩率）、bpp（编码率）、MSE，PSNR作为度量压缩性能的4个指标.压缩解压后的实验结果见表1、表2.

表1 压缩性能对比（bpp，CR）

由表1、表2可见，当增加循环次数时，最终2种算法的4种压缩量化指标都可以取得极值，并且该极值基本相同，此时小波域的所有重要系数全部被编码.但是在循环次数较低的情况下，既低比特率的情况下TP－SPIHT算法性能明显优于SPIHT算法.图9为当循环次数为11时，重构信号与原始信号的误差.

表2 压缩性能对比（MSE，PSNR）

图9 重构信号与原始信号误差

由图9中可见，对于最大值为±421.8V的电能质量含噪故障信号，压缩解压后的误差在±0.6V之内，误差精度满足要求.可见TB－SPIHT算法可以很好的完成电能质量信号的压缩任务.

5 结束语

因为电能质量信号有其自身的特点，对于绝大部分采样信号，其都会含有幅值为380V、频率为50HZ的基波信号，对于压缩解压端来说，这部分的信息可以视为已知的冗余信息，所以并不需浪费编码位.为了解决这一问题，文中提出了一种基于模板的电能质量数据压缩方案TB－SPIHT.并将其与传统二维小波压缩算法进行了实验对比，结果表明TB－SPIHT算法在压缩效果上优于SPIHT算法，特别是在压缩比方面有了近一个数量级的提高.

［1］肖湘宁，徐永海.电能质量问题剖析［J］.电网技术，2001，25（3）：66－69.

［2］张 斌，刘晓川，许之晗.基于变换的电能质量分析方法，2001，25（1）：26－29.

［3］张 昊，刘 沛.基于双正交小波的电力系统故障录波数据压缩［J］.电网技术，2002，24（11）：42－45.

［4］欧阳森，宋政湘，陈德桂，等.基于小波原理的电能质量检测数据实时压缩方法［J］.电网技术，2003，27（2）：37－40.

［5］闫常友，杨奇逊，刘万顺.基于提升格式的实时数据压缩和重构算法［J］.中国电机工程学报，2005，25（9）：6－10.

［6］刘志刚，何正友，钱清泉.基于最优预处理方法的多小波故障数据压缩方案［J］.电网技术，2005，29（11）：40－43.

［7］GEREKÖN，ECE D G.2－D analysis and compression of Power－Quality event data［J］.IEEE Transactions on Power Delivery，2004，19（2）：791－798.

［8］高培生，陈新建，吴为麟，等.二维表示的电能质量故障数据压缩［J］.浙江大学学报，2008，42（4）：686－690.

［9］张 明，李开成，胡益胜.基于JPEG2000的电能质量扰动数据压缩方法［J］.电工技术学报，2011，26（10）：47－53.

［10］张建军，姚晓波.一种改进的零树小波编码图像压缩算法［J］.武汉理工大学学报：信息与管理工程版，2006，（1）：4－6，10.

［11］鲍 文，周 瑞，刘金福.基于二维提升小波的火电厂周期性数据压缩算法［J］.中国电机工程学报，2007，27（29）：96－101.

［12］刘 毅，周雒维，冯 浩.电能质量监测网录波数据压缩方法［J］.电网技术，2010，34（4）：199－203.

［13］DAUBECHIES I.SWELDENS W.Factoring wavelet transforms into lifting steps［J］.Journal of Analysis and Application，1998，4（3），247－269.

［14］SWELDENS W.The lifting scheme：a custom design construction of biorthogonal wavelets［J］.Appl.Comut.Harmon，1996，3（2）：186－200.

［15］SAID A，PEARLMAN W A.A new，fast，and efficient image codec based on set partitioning in hierarchical trees［J］.IEEE Transactions on Circuits and Systems for Video Technology，1996，6（3）：243－250.