水泥混凝土桥梁双层桥面铺装结构力学分析＊

赵岩荆 蒋 玲

（南京交通职业技术学院 南京 211188）

0 引 言

在车辆荷载和自然环境交替作用下，水泥混凝土桥面铺装易出现推移、拥包、裂缝、坑洞、桥面渗水等早期破坏［1］.而对于桥面铺装层使用性能而言，铺装层材料的选择以及铺装层结构的设计是主要影响因素［2］.随着桥面铺装技术的发展和进步，高强度、高模量等高性能沥青混凝土材料已经被越来越普遍的应用于桥面铺装中［3］.在钢桥面铺装中，广泛应用的环氧沥青混凝土也被考虑引进水泥混凝土桥梁铺装层应用之中.然而由于环氧沥青混凝土造价昂贵，因此在研究中考虑“下层环氧沥青混凝土＋上层普通改性沥青混凝土（如SBS改性沥青混凝土）”的铺装层结构，以期在提高铺装层性能的同时，能够保持合理的经济性.

由于环氧沥青混凝土具有强度大，模量高的特点［4］，其应用于水泥混凝土桥面铺装层时所产生的力学响应与采用传统材料的铺装层必然有所差异，因此有必要进行相应的力学分析.同时，水泥混凝土桥梁铺装层的边界条件要明显强于钢桥面铺装.故已经在大跨径钢桥面铺装中得到实际工程验证的环氧沥青混凝土在水泥混凝土桥梁中发生病害的可能性更低，因此本文主要研究在下面层材料变化时，上面层即普通改性沥青混凝土铺装层的力学响应变化规律.以研究应用环氧沥青混凝土对于铺装层受力分析的影响效果.

桥梁结构形式多种多样，桥梁的跨径也不尽相同.因此，对于不同结构，不同跨径的桥梁，采用何种铺装层材料组合最为合理，对铺装层结构的优化和设计具有十分重要的意义［5－9］.同时，铺装层下面层对上面层力学响应的影响主要源自下面层材料自身的模量.故本文选取两种典型的水泥混凝土桥梁结构形式：水泥混凝土空心板桥及水泥混凝土工字梁桥，分别建立2种桥梁结构在不同跨径状态下的三维有限元模型，针对不同桥梁结构形式、不同桥梁跨径，以及不同模量的下面层，研究铺装层上面层在车辆荷载下的力学响应.最终得出环氧沥青混凝土在水泥桥梁铺装层下面层中应用的可行性和适用性.

本研究利用三维有限元建模技术，依据桥梁实际尺寸，利用ABAQUS有限元分析软件建立整桥模型，从而能够合理反映桥梁整体结构变形对铺装层力学响应的影响，能够有效提高力学分析结果的合理性与可靠性。

1 计算模型的建立

1.1 桥梁有限元模型的建立

本研究中所选用桥梁均为多跨简支梁结构，各跨几何参数及边界条件几乎完全相同，故只需选取一个跨段的铺装层作为分析对象即可.同时，为考虑相邻跨段结构的影响，亦将其纳入建模范围.最终，选择总计3个跨段为建模对象，其中中间跨段铺装层为主要研究对象.在此基础上计算其荷载作用下的应力应变响应［10］.模型效果见图1～2.

图1 工字梁桥有限元模型

图2 空心板桥有限元模型

1.2 材料及结构参数

桥梁结构及铺装层分别由钢筋水泥混凝土与改性沥青混凝土构成，本文对钢筋水泥混凝土及改性沥青混凝土的材料参数如不作特殊说明，均按表1中所列参数取值［11］.

表1 材料及结构参数

而铺装层下面层模量则作为变量，以2 000 MPa为区间，在2 000MPa～10GPa之间，取5个不同的模量，计算铺装层上面层在此条件下的力学响应.同时结合工程实践及实际铺装应用，设定桥面铺装层总厚度为6cm，其中上下面层厚度各为3cm.

1.3 荷载作用形式

本研究所采用的车辆荷载的立面、平面尺寸见图3.

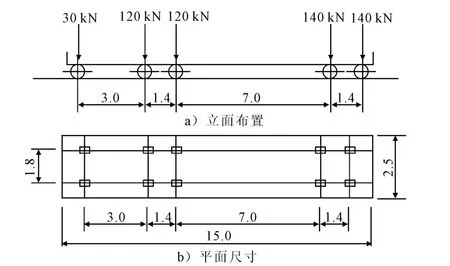
图3 车辆荷载的立面、平面尺寸（尺寸单位：m）

车辆荷载的主要技术指标见表2.

表2 车辆荷载主要技术指标

本研究中各轮胎接地压强均取为0.707 MPa［12］.而由于接地压强取值不同而导致的轴重增大，也符合中国道路普遍具有交通量大，重载车辆多的特点［13－15］，并且计算结果偏安全.

车辆在行使过程中由于车辆制动，轮胎与路面接触面上将会产生水平应力.水平荷载可由下式决定

式中：T为水平荷载；φ为滑动摩阻系数；P为车辆的垂直荷载.

本文取水平力系数分别为0.3，并在此基础上，对沥青混凝土铺装层力学响应进行分析.

车辆荷载作用分布以及最不利荷位由文献［14］所述方法确定，本文限于篇幅，省略其计算过程.

2 空心板桥计算结果

空心板桥通常跨径为10～30m.因此，本文选择10，20及30m作为3个不同的跨径.空心板桥铺装层上面层力学响应计算结果见图4.

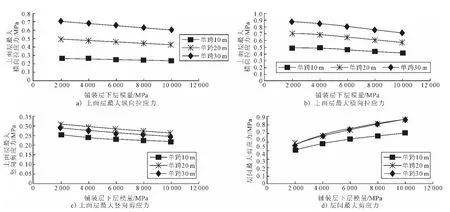
图4 空心板桥铺装层力学响应

由图4可见，铺装层上面层的最大纵向拉应力、最大横向拉应力以及最大竖向剪应力均随着下面层模量的增长而呈下降趋势，表明下面层模量的提高有利于改善上面层受力状态，对抑制上面层发生开裂破坏以及车辙病害均由一定的作用效果.而图4d）则反映了铺装层上下面层层间剪应力水平随着铺装层下面层模量的增长而提高，因此下面层模量的增长对层间粘结层抗剪性能提出了更高的要求.

通过观察图4可知，不同跨径空心板桥铺装层上面层力学响应规律虽趋向一致，但是数值水平却有所不同.上面层最大纵向及横向拉应力水平均随着桥梁跨径的增长而提高.因此，为更清晰的对比下面层模量对不同跨径桥梁铺装层力学响应所带来的影响，计算各力学指标在下面层模量由2 000 MPa上升至10 000MPa时的变化幅度.见图5.

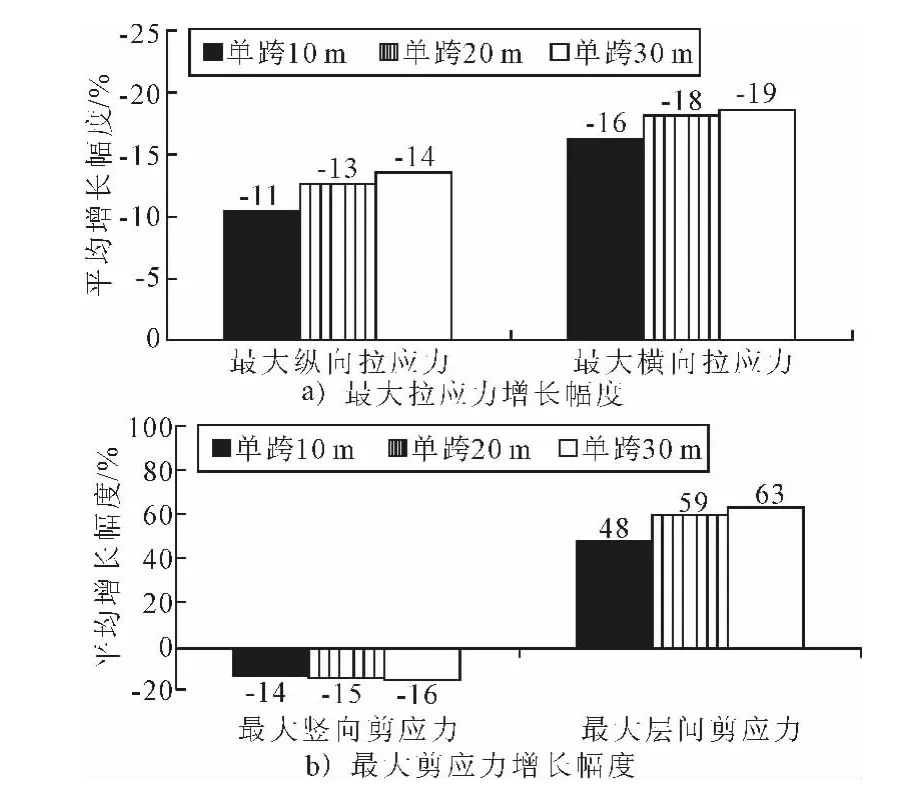
图5 铺装层力学响应变化幅度

由图5a）可知，当下面层模量变化时，上面层最大纵向拉应力及最大横向拉应力变化幅度均随着桥梁跨径的增大而增长.因此大跨径空心板桥铺装层上面层拉应力对下面层模量的变化更为敏感.换而言之，即对于同样的下面层模量增长幅度，更大跨径桥梁的上面层拉应力降低幅度更大.结合图4a）～b），桥梁跨径的增长将导致上面层拉应力的显著增长，使得上面层拉应力距离材料极限抗拉强度更为接近，产生开裂破坏的可能性越大.因此，在大跨径桥面铺装设计中，应用高性能沥青混凝土（如环氧沥青混凝土）作为下面层，对抑制上面层产生裂缝病害，效果尤为明显.

如图5b）中所示，最大竖向拉应力变化幅度受跨径影响不大，差别很小.结合图4c）可以得出，无论何种跨径桥梁，下面层模量的增大均能够抑制车辙病害的发生与扩展.最大层间剪应力的增长幅度随着桥梁跨径的增大而增长，但如同图4d）中所示规律一样，20m与30m桥梁铺装层层间剪应力十分接近，但均大于10m跨径的桥梁.因此可以得出，铺装层上下面层层间剪应力水平基本上随着桥梁跨径的增大而增长，且随着下面层模量的增长而成显著上升趋势.因此，在下面层应用如环氧沥青混凝土之类的高强度沥青时，必须对铺装层上下面层之间的粘结层抗剪性能提出更高的要求，采用诸如环氧沥青粘结层之类高性能粘结层材料，以保证在合理改善铺装层受力状态的同时，避免层间发生错动滑移等病害，保证铺装层的正常使用.

3 工字梁桥计算结果

工字梁桥跨径范围一般介于20～50m之间.由于50m跨径的工字简支梁桥应用并不十分广泛，因此本文分别选取跨径为20，30及40m的3座工字梁桥作为分析原型，对其铺装层力学响应进行分析.

计算结果见图6.

图6 工字梁桥铺装层力学响应

图6显示了各不同跨径的工字梁桥铺装层上面层力学响应指标随下面层模量变化的规律.由结果可知，工字梁桥计算结果与空心板桥计算结果基本一致，均是上面层最大纵向及横向拉应力，以及最大竖向剪应力随着下面层模量的增大而减小；而层间剪应力水平则随之提高.为衡量不同跨径对上面层力学指标变化规律的影响，计算下面层模量由2 000MPa上升至10 000MPa时上面层力学指标变化幅度，见图7.

图7 铺装层力学响应变化幅度

由图6～7可知，较大跨径的工字梁桥铺装层上面层拉应力水平受到下面层模量变化的影响更大；而上面层最大竖向剪应力及层间最大剪应力则受桥梁跨径的影响并不十分明显.但是最大竖向剪应力也同样随着下面层模量的增大而减小，而最大层间剪应力则随着下面层模量的增大而增长.因此，工字梁桥铺装层上面层力学指标随下面层模量的主要变化规律与箱梁桥基本一致.

4 结 论

1）在车辆荷载作用下，对于空心板梁桥与工字梁桥而言，无论其跨径长度如何，其铺装层上面层最大拉应力（包括纵向及横向）均随着下面层模量的增长而降低；考虑到大跨径桥面铺装层的拉应力水平更加接近于材料极限抗拉强度，以及大跨径桥面铺装层力学响应对下面层模量的变化更敏感，因此通过提高下面层模量来降低铺装层上面层发生开裂破坏的可能性及严重性，对于大跨径桥梁而言，具有更加积极的意义.

2）铺装层最大竖向剪应力水平均随着下面层模量的增长而降低，因此较大的下面层模量能够显著降低上面层发生车辙病害的可能性.同时由于下面层采用较高模量的材料（如环氧沥青混凝土），其本身的抗车辙性能便已十分优异，因此对于铺装层结构整体的抗车辙性能而言，具有很大的提升作用.

3）铺装层上下面层之间的层间剪应力随着下面层模量的增长而呈显著增大趋势.因此在铺装层下面层应用较高模量材料的情况下，必须对层间粘结层性能提出更高的要求，确保铺装层的正常使用.

［1］陈太泉.水泥混凝土桥沥青铺装层力学分析与设计［D］.武汉：武汉理工大学，2007.

［2］张领先.水泥混凝土桥桥面铺装层结构合理性研究［D］.重庆：重庆交通大学，2008.

［3］李洪涛，黄 卫.润扬大桥钢桥面铺装实桥试验研究［J］.公路交通科技，2005，22（4）：76－78.

［4］王晓，程刚，黄 卫.环氧沥青混凝土性能研究［J］.东南大学学报：自然科学版，2001，31（6）：21－24.

［5］钱振东，黄 卫，骆俊伟，等.正交异性钢桥面铺装层的力学特性分析［J］.交通运输工程学报，2002，2（3）：47－51.

［6］邓强民，倪富健，顾兴宇，等.大跨钢桥桥面铺装有限元分析合理简化模型［J］.交通运输工程学报，2008，8（2）：53－58.

［7］徐 伟，李 智，张肖宁.子模型法在大跨径斜拉桥桥面结构分析中的应用［J］.土木工程学报，2004，37（6）：30－34.

［8］CHUNG W，ELISA D S.Three dimensional finite element modeling of composite girder bridges［J］.Engineering Structures，2006，28：63－71.

［9］LESLAW K，LI Hongyi，WEKEZER J，et al.Finite element analysis of vehicle－bridge interaction［J］.Finite Elements in Analysis and Desigh，2006，42：950－959.

［10］Hibbitt，Karlsson ＆ Sorensen，Inc.ABAQUS／Standard User’s Manual；ABAQUS／CAE User’s Manual；ABAQUS Keywords Manual；ABAQUS Theory Manual［M］.USA：HKS CO.，2002.

［11］于 颖.水泥混凝土桥桥面铺装受力机理分析［D］.重庆：重庆交通大学，2008.

［12］许 涛，黄晓明，高雪池.移动荷载作用下沥青混凝土桥面铺装层动力响应分析［J］.公路交通科技，2007，24（10）：6－10.

［13］曾凡奇，黄晓明.超载对沥青路面的影响［J］.交通运输工程学报，2004，4（3）：8－10.

［14］李 昶，邓学钧.荷载对铺装层应变的影响［J］.公路交通科技，2002，19（2）：60－62.

［15］吴一鸣.大跨径钢桥桥面铺装力学深入研究［D］.南京：东南大学，2005.