一种新型滤波PID控制器设计

简晟祺，魏延辉，王 刚，王泽鹏

（哈尔滨工程大学自动化学院，黑龙江 哈尔滨150001）

0 引言

目前，许多新的控制策略被应用在机器人领域，包括：自适应控制、遗传算法、鲁棒控制和模糊控制等。自适应控制策略能够对参数不确定性进行辨识，但难以处理外部扰动等非参数不确定［1］。遗传算法具有很好的鲁棒性，但搜索和寻优过程耗时长，控制的实时性不好。而鲁棒控制需要保守的不确定上界估计，变结构控制存在“抖振”［2］。普通的模糊控制综合定量只是的能力差，控制规则和隶属函数一经确定便无法修改，不具备自学习、自适应的能力。因此，不能很好地控制不确定系统［3］。

虽然智能控制发展迅速，但由于代码复杂、实现困难等原因，在实际中应用得并不多。而PID控制是实际工程领域使用最多，应用层面也最广的控制器。PID控制具有结构简单、稳定性能好和可靠性高等优点，尤其适用于可建立精确数学模型的确定控制系统。在控制理论和技术飞速发展的今天，工业过程控制领域仍有近90%的回路在应用PID控制策略。PID控制中一个关键问题便是PID参数的整定［4］。并且很多情况下，为了参数整定的方便而舍本逐末地去掉微分环节。

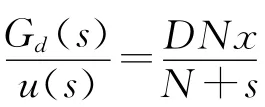
Matlab中的Simulink控制箱是常用的建立自控系统仿真环境的工具，Simulink给进行系统仿真提供了很大的方便。通过利用Matlab 2012a版本中的Simulink所介绍的PID Tuner参数，自动整定的新功能，并且将它应用在电机运动的控制中，取得较好的效果。

1 传统PID控制原理及参数的影响

PID的控制规律为：

KP为比例系数；Ti为积分时间常数；Td为微分时间常数。传统PID的框图如图1所示，写成传递函数的形式为：

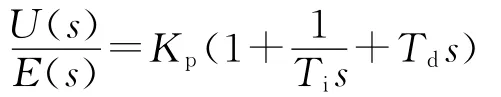
图1 传统PID

a.比例系数Kp。增大比例系数Kp，能够加快系统的响应速度，增强系统的动态性能并能见效系统的稳态误差。但如果比例系数过大，效果反而适得其反，系统的超调增大，调节时间更长，系统甚至会震荡变得不稳定。

b.积分时间常数Ti。增大积分时间常数Ti，能够减小稳态误差，增强系统的稳定性。但调节时间会变长，使系统的动态性能变差。

c.微分时间常数Td。增大微分时间常数Td，能够增大微分作用，能够减小调节时间，减小稳态误差，增加系统的控制精度，提高系统的稳定性。但微分时间常数过大或过小，系统的超调量会增加，精度减弱，产生噪声。

可以看出，这3个参数对于典型PID控制器的控制效果起到只管总要的作用。为了取得好的控制效果，工程人员需要花费大量的时间在这3个参数的调整上。总之，比例主要用于偏差的“粗调”，保证控制系统的“稳”；积分主要用于偏差的“细调”，保证控制系统的“准”；微分主要用于偏差的“细调”，保证控制系统的的“快”［7］。

2 滤波PID的原理及实现

实际工程应用中难免会引入干扰，比如在PID或PD控制器的微分过程中加入高通滤波器，组成新的PID系统框图，滤波PID框图如图2所示。

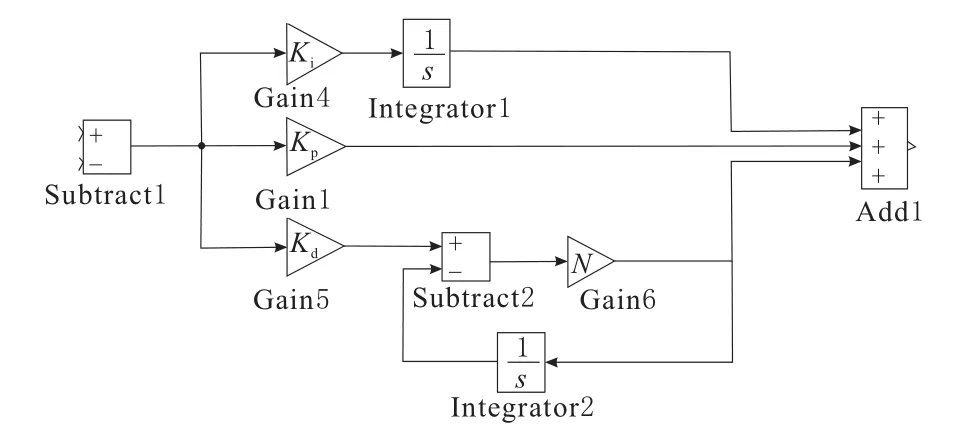
图2 滤波PID

微分环节对整个模型的动态变化很敏感，输出结果容易受到影响。因此，很多人出于参数整定麻烦和系统稳定性的考虑而选择去掉微分环节而使用PI控制器，舍本逐末地牺牲了微分环节在系统动态性能调整的作用。鉴于机器人控制中误差的引入多为摩擦或是啮合，相对于控制信号而言算是低频干扰，所以可以加入一个高通滤波器，滤除干扰来优化PID控制器的动态性能。

高通滤波器是对输入信号的频率具有选择性的一个二端口网络，它允许输入信号中高于某频率的信号通过，而衰减或抑制小于此频率的信号［8］。加入滤波器后整个微分环节的传递函数为：

而整个滤波PID控制器的传递函数为：

可以看出，通过设置参数N而改变这个滤波器的极点位置，从而改变滤波器的滤波效果，最终影响到整个微分环节的作用效果。

通过改变N的大小，就可以改变滤波器的幅频特性和相频特性，N越大便极点越靠近负半轴，对于低频信号的滤波效果就越明显。加入滤波后的PID控制器还需要用C语言实现编写，以下便是代码实现：

FilterCoefficient＝N ＊ （Kd＊u－Filter＿state）；

Filter＿State＋＝0.01＊FilterCoefficient；

Integrator＿State＋＝Ki＊u＊0.01；

Y＝（Kp＊u＋Integrator＿state）＋FilterCoefficient；

u为偏差量，FilterCoefficient为滤波系数。等式中的0.01为采样时间，单位为s，根据系统的实际情况作调整。

3 电机控制的建模仿真和验证

3.1 电机模型及系统的建立

以电机的电枢电压为输入，以电机的角位移为输出，则直流电机的模型如图3所示。

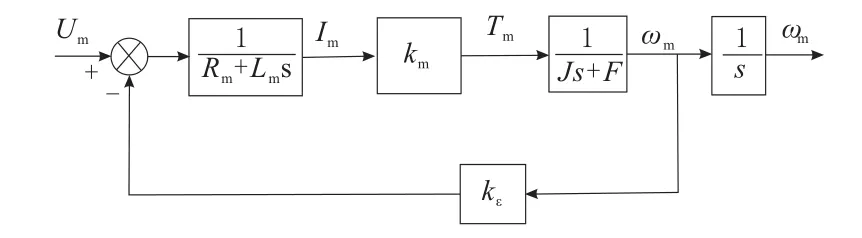
图3 直流电机模型

Rm为电枢电阻；Lm为电枢电感；km为电流－力矩系数；J为总转动惯量；F为总粘滞摩擦系数；ke为反电动势系数；Um为电枢电压；Im为电枢电流；Tm为电机力矩；ωm为电机角速度；θm为电机角位移［9］。所以可得到直流电机的系统框图如图4所示。

于是可以得到电直流电机的传递函数为：

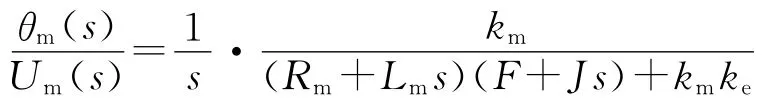
使用Faulhaber公司的2342直流电机，查阅相关技术手册可以得到每个参数的大小。因为粘滞摩擦系数很小可以忽略不计，所以将参数带入等式，可以得到电机的传递函数为：

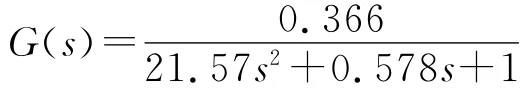
这样便可以建立具有速度控制环和角度控制环双闭环控制的PID控制系统。

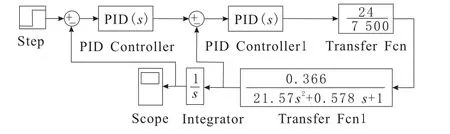
图4 系统框图

在Matlab 2012a中加入的PID Tuner，大大方便了对PID参数的整定，PID Tuner提供了快速求解PID参数的解决方案。PID Tuner会先为实际模型计算一个线性模型，即使系统中存在非线性系统也会自动并估计出一个线性模型。然后再将整个系统接在这个线性模型的输入和输出上并自动计算一组初始PID参数，这组参数是综合计算了系统的鲁棒性和快速性得到的。它还会对比当前设置的PID参数与系统计算的PID参数的控制效果，它们都是闭环系统的阶跃相应，所以对控制系统设计有一定的参考价值。

可以通过设置想要的系统响应时间，来进行PID参数的整定。在这个系统机器人控制系统中有速度环和角度环2个PID控制器，这2个闭环存在耦合会相互影响，如果采用试凑的方法想得到鲁棒性很好的两组参数很困难。而通过PID Tuner可以很快确定一组参数。

3.2 仿真及验证

以使用Faulhaber公司的2642WO24R直流无刷电机作为例子。通过查找该型号电机的技术手册，可以得到它的几个建模关键参数。

可以得到传递函数：

将这组参数输入传统PID控制器，得到仿真结果如图5所示。不难看出系统发散 ，由于没有高通滤波器，微分环节使系统超调过大，调节时间过长，系统最后呈不稳定状态。

将同样的数据输入滤波PID控制器，得到仿真结果如图6所示。系统的超调还是稳态误差都控制的很好，系统的响应速度也很快。

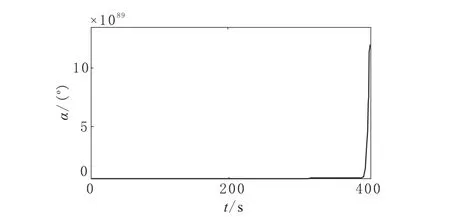
图5 传统PID仿真结果

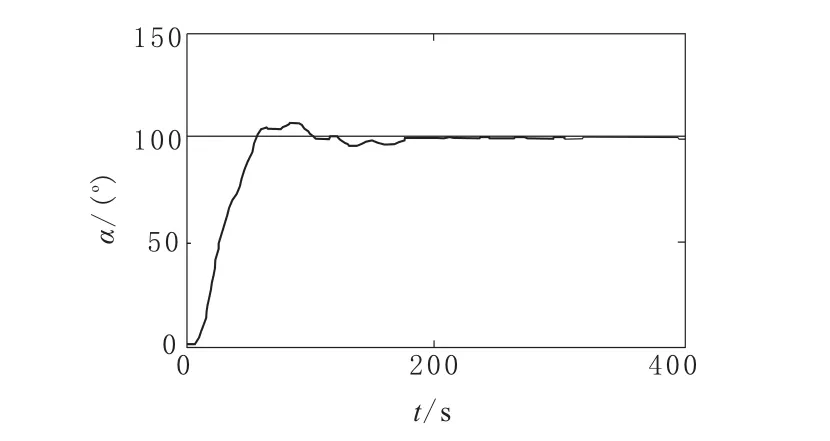
图6 滤波PID仿真结果

为了验证仿真结果，用C＃编写了上微机监控软件，能够实时反馈电机角度的变化。由于CAN总线的数据传输速度远大于上位机软件的刷新频率，所以实时角度曲线会有锯齿，但这并不影响用户观察电机实时角度的变化趋势。实验验证结果如图7所示。

图7 电机的实时角度

4 结束语

设计的高通滤波器在微分环节的抗干扰性能上作用明显，增强的系统的稳定性。在控制系统中引入滤波PID并配合PID Tuner，能提高工程人员在设计控制系统时的工作效率，让PID的参数整定过程更科学、更智能和更高效，从而缩短控制系统的研发周期。鉴于PID控制的广泛性，这种方法具有很高的应用价值。

［1］ 张文辉，胡小平，朱银发.自由漂浮空间机械臂基于神经网络的 H∞鲁棒控制［J］.应用科技，2012，（6）：5－8.

［2］ Machado J A T.Variable structure control of manipulators with compliant joints［A］.IEEE International conference industrial.Electron［C］.London，UK，1993.554－559.

［3］ 洪昭斌，陈 力.基于神经网络的漂浮基空间机械臂的自学习模糊控制［J］.机械科学与技术.2009，28（7）：976－980.

［4］ 沈永福，吴少军，邓方林.智能PID控制综述［J］.工业仪表与自动化装置.2002，（6）：11－13.

［5］ 王素青，姜维福.基于 Matlab／Simulink的PID参数整定［J］.工业控制与应用.2009，28（03）：24－28.

［6］ 何 颖，鹿 蕾，赵争鸣.PID参数自整定方法概述［J］.仪器与仪表.2004，（24）：20－23.

［7］ 白 金，韩俊伟.基于 Matlab／Simulink环境下的PID参数整定［J］.哈尔滨商业大学学报（自然科学版），2007，23（6）：673－676.

［8］ 郗艳华，张玉叶.高通滤波器分析及其仿真［J］.信息技术.2011，（8）：29－31.

［9］ 谭为民，徐 德，侯增广，等.先进机器人控制［M］.北京：高等教育出版社，2007.