基于槽式太阳能聚光器结构的流固耦合分析

2014-04-10朱天宇

机械与电子 2014年5期

林红，肖洪，朱天宇，王磊

（1.河海大学机电工程学院，江苏常州213022；2.南通河海大学海洋与近海工程研究院，江苏南通226019）

0 引言

槽式太阳能聚光器通过对太阳光的聚焦，加热集热器内的工质，为电站的蒸汽产生系统提供高温热源或直接将高温蒸汽提供给汽轮机［1］。因此，聚光器是太阳能热发电系统的核心部件，它的性能的好坏会显著影响太阳能热发电系统的总体性能［2］。

槽式太阳能聚光器始终工作在露天的环境中，不可避免地会受到环境的影响，尤其是风载荷。重庆大学机械传动国家重点实验室的胡摇等人，采用计算流体力学（CFD）理论建立了计算模型，分析了槽式太阳能聚光器在不同角度、不同风速、不同反光镜间缝隙下对风载荷的影响［3］。重庆大学机械传动国家重点实验室的孔祥兵等人，利用流体仿真软件FLUENT来模拟风场，然后将得到的最大面载荷施加在镜面上，应用ABAQUS软件对槽式太阳能聚光器的结构进行有限元分析［4］。河海大学的刘英玉等人通过风速与风压的换算关系，将换算的风压施加到镜面上，采用ANSYS软件对槽式太阳能聚光器结构进行分析［5］。这些方法没有将流场和结构的计算结合起来进行分析。随着计算机技术的发展以及现代分析方法的不断改进，流固耦合分析方法成功的将流场和结构的计算结合起来，使得槽式太阳能聚光器的流固耦合技术得以实现［6］。因此，有必要对槽式太阳能聚光器进行流固耦合分析。

1 流固耦合理论

1.1 流体控制方程

流体流动必须遵循基本的物理守恒定律，其中包括质量守恒定律、动量守恒定律和能量守恒定律。不考虑流体、固体间的能量传递，对能量守恒不进行描述［7］。

质量守恒方程为：

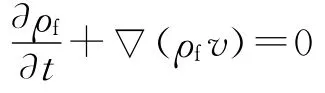
动量守恒方程为：

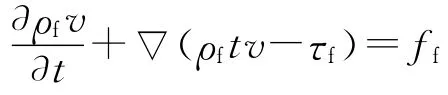
ρf为流体密度；t为时间；v为流体速度矢量；τf为剪切力张量；ff为体积力矢量。

1.2 固体控制方程

固体部分的守恒方程由牛顿第二定律导出：

ρs为固体密度；ds为固体域当地加速度矢量；σs为柯西应力张量；fs为体积力矢量。

1.3 流固耦合方程

同样，流固耦合也遵循一些最基本的守恒原则。因此，在流固耦合交界面处，应满足流体与固体应力τ、位移d、热流量q和温度T等的相等或守恒，即满足以下4个方程：

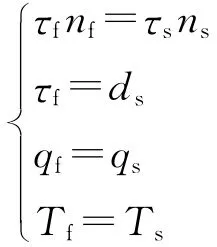
下标f，s分别为流体、固体。

采用ANSYS Workbench软件对槽式太阳能聚光器在不同风速、不同工作角度下进行单向流固耦合分析。聚光器流固耦合分析流程如图1所示。

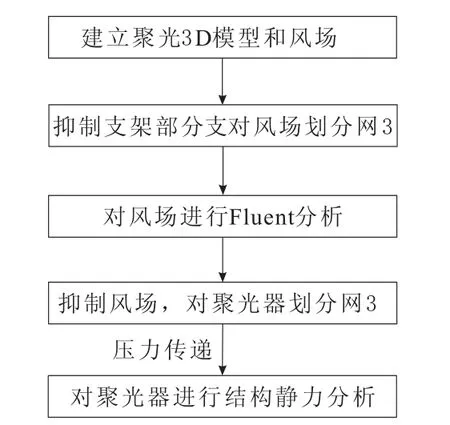
图1 流固耦合分析流程

2 流场分析

2.1 建立有限元模型

利用Workbench对槽式太阳能聚光器进行有限元建模，取水平横向为X轴，竖直方向为Y轴，水平轴向为Z轴。根据抛物线聚光原理，槽式太阳能聚光器工作时的位置是随太阳方位角的变化而发生变化，这里选取0°、30°、60°、90°、120°、150°和180°进行分析计算。其中0°与90°的有限元模型如图2所示。

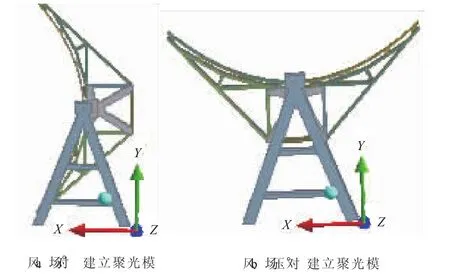
图2 聚光器的有限元模型

2.2 流场的建立与设置

流场数值分析时将支架部分抑制的原因是：支架部分为金属框架，对流场进行有限元网格划分时，会产生大量的网格单元，增加计算量；流体模型变得复杂，网格划分质量降低，影响分析结果的精度；支架部分受到风载荷的影响与反光镜部分的影响相比非常小，可以忽略不计。

将流体模型导入ANSYS Workbench下的Fluent中进行数值模拟，进行湍流方程设置，选择Viscou－Stannard中的标准k－epslion模型；流动介质为空气，假设空气为不可压缩流体；入口采用速度边界条件，风的方向与X轴平行，设置额定速度为六、七、八级风的最大风速［8］；出口使用压力边界条件，压力设为0；利用Simple算法及定常稳态求解器进行求解。

3 聚光器的结构分析

3.1 结构分析前处理

槽式太阳能聚光器支撑结构的材料为Q235A钢，选择ANSYS Workbench中的Structural Steel即可。同时添加反光镜的材料浮法白玻，命名为glass。浮法白玻为脆性材料，它的常见破坏形式为断裂失效。最大拉应力理论（第一强度理论）是解释脆性材料断裂失效的原因，该理论认为最大拉应力是引起断裂的主要因素。即认为无论是什么应力状态，只要最大拉应力达到某一极限值，材料就发生断裂［9］。由于失效的原因与应力状态无关，也就是最大拉应力的极限值与应力状态无关。因此，要设置浮法白玻的拉应力极限值（tensile yield strength）。

聚光器所受约束为4个支撑脚施加固定约束，限制聚光器X，Y，Z方向的移动和绕X，Y，Z的转动。尽管聚光器跟随太阳转动，但它的转动是间歇性的、缓慢的，分析时将整个聚光器结构视为刚连接。

聚光器所受载荷为惯性载荷和压力载荷。惯性载荷是重力，方向为Y轴负向，将其施加到整个聚光器上。压力载荷为来自流体分析的压力数据并作用在反光镜的表面。图3所示为导入的反光镜压力图（工作角度为60°）。

图3 反光镜压力（60°）

3.2 计算结果及分析

以八级风作用、工作角度为60°的结果为例进行结果分析。聚光器结构的变形、应力、最大拉伸应力安全系数结果如图4～6所示。

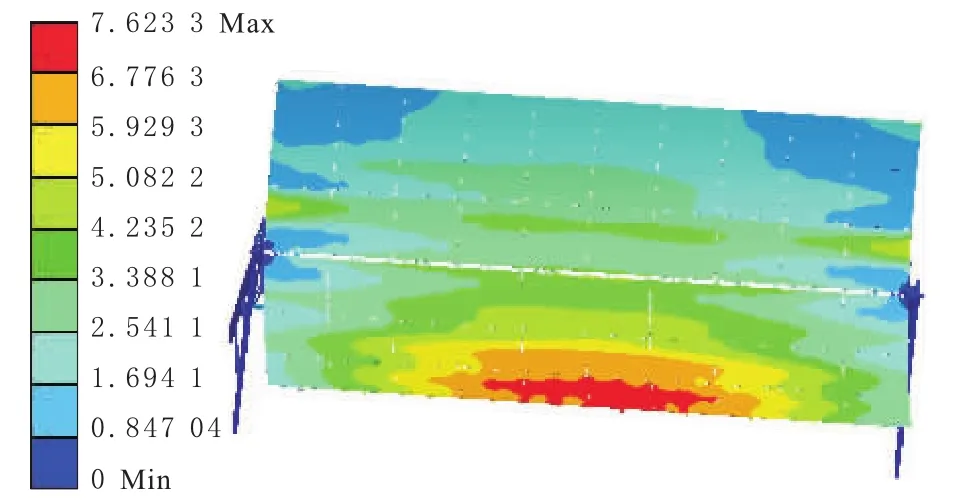
图4 聚光器整体变形

图5 聚光器的应力分布

图6 聚光器的拉应力安全系数

由图4可见，聚光器中间部分变形比较明显，特别是靠近反光镜的边缘部分，最大值为7.623 3 mm，这是聚光器沿Z轴方向较长的原因。由图5可知，应力较大的部分出现在矩形框架的两端，最大值为86.18MPa这是因为这两端承受的力矩比较大。由图6可以得到，反光镜在支撑端附近的最大拉应力安全系数较小，最小值为2.469。通过以上结果分析，聚光器结构设计在刚度和强度上均满足要求。

聚光器在不同工作角度受六、七、八级风作用下的最大变形、最大应力、最小安全系数如图7所示。