考虑碳交易的供应链环境下产品定价与产量决策研究
2014-04-10马秋卓宋海清陈功玉
马秋卓,宋海清,陈功玉
(中山大学岭南学院,广东 广州 510275)
1 引言
温室气体的大量排放被认为是导致全球变温的直接原因之一[1]。由于《京都议定书》中所规定的六种温室气体中含碳含量占一半以上,所以温室气体的排放一般也被称为“碳排放”。随着社会对此问题的日益重视,越来越多的国家正着手制定低碳、环保的相关法律法规,并建立碳交易体系。中国已经做出了至2020年的减排承诺[2],并逐步建立类似于欧盟EU ETS体系的碳交易市场[3]。本文基于欧盟的ETS及中国各试点地区的碳交易模式[4],考虑了一个由多供应商、多制造商、多产品市场和一个碳交易中心组成的供应链系统。其中,实体流网络由供应商、制造商及市场三方构成;碳金融网络由供应商、制造商及碳交易中心构成。基于这一特定问题,我们利用变分不等式建立了一个超网络模型,研究了供应链各方处于均衡状态时最优的产品定价及产量决策。基于比较成熟的修正型投影算法,我们通过数值例子求解了上述模型并对比分析了有、无碳交易两种情况下的企业决策及供应链整体绩效,为企业决策及政府政策的制定提供了建议。
相关的文献主要包括,Du等[6]描述了一个以碳排放为主的制造企业及掌握碳配额的非盈利性供应商组成的供应链。在报摊模型的背景下,作者分析了各决策者之间关于产品定价与产量的博弈,得出了唯一的纳什均衡。Diabat与Simchi-Levi[7]考虑了环境及供应链绩效等目标,利用混合整数规划(MIP)寻找政府低碳政策下企业最优的应对策略。Chaabane等人[8],利用混合整数线性规划(MILP)探讨了温室气体交易背景下,包括多期环境与经济目标在内的供应链设置问题。类似的,Hugo与Pistikopoulos[9]将LCA(Life Cycle Assessment)作为测量环境绩效的一项指标,利用MIP基于供应链网络考虑了环境与经济的多目标优化问题。Abdallah[10]利用MIP构建了一个低碳敏感型供应链。发现该供应链上的核心企业在对供应商提出低碳环保要求的同时也承担着发展低碳供应链所带来的较高的成本。Giarola[11]利用MIP讨论了面对不确定性市场的多期多级乙醇供应链设计问题,发现企业加入碳交易体系将获得成本效率的提升。Bojarski[12]探讨了环境、经济多目标优化下的供应链设计问题。
本文与Du等[6]的研究不同之处在于,我们基于一个网链式的供应链结构,同时考虑了多个博弈参与人及相互之间的均衡决策。对于Diabat与Simchi-Levi[7]的研究,虽然在作者所描述的问题之中存在多个决策者,但所考虑的网络结构为单层结构且未涉及博弈等问题。较Diabat与Simchi-Levi[7]的研究,Chaabane等[8]以及Hugo与Pistikopoulos[9]的研究成果中,网络结构更为复杂,涉及更多的参与人与更多的供应链级别,但本质上仍为单层结构。我们的研究不仅考虑了企业与企业,企业与市场之间的商品流、资金流,还在第二层网络之中引入碳交易中心,探讨了它与碳交易机制下各企业之间的交易活动。另外,我们考虑企业、碳交易中心之间完全以市场为向导的碳额度交易过程,而并未涉及外生的强制性碳排放量约束。而在Chaabane等[8]的研究之中,生产经营过程中所产生以及每期企业可以购买或出售的排放量均受限于某个已知的额度。与Abdallah[10]及Giarola[11]的研究相比,本文不仅对碳交易机制下整个供应链的绩效水平感兴趣,还有意于探讨供应商与制造商等参与人之间因生产及碳交易活动所带动的利润分配情况。从方法上来看,上述研究主要以MIP为主。然而,有学者认为MIP模型对非线性、多目标决策等问题表现欠佳。Wang Zhiping等[13]认为利用超网络理论结合变分不等式模型可以较好地克服这一缺点。根据王志平,王众托[14]对文献[15]与[16]所做的回顾,最早使用超网络一词的是Sheffi[15]。之后,Nagurney[16]对超网络系统无论在理论或是应用上的推广都做出了很大的贡献。不过据我们所知,以往的研究中将变分不等式应用于低碳供应链问题的文献并不多见。虽然Wu Kai等[17]借交通流平衡超网络模型,分析了电力供应链上不同电厂的选择组合及碳税对企业决策的影响,还有Nagurney等[18]分析了电力供应链上政府的最优碳税决策,但与这些研究不同的是,我们将模型构建在一个更一般的供应链网络之上,具有更好的普适性。而当我们加入碳交易中心作为一个新的决策制定者时,因为能够更好地模型现实情况,模型在低碳供应链问题上又具有更强的针对性。与这种框架类似的有Nagurney等[19-20]将金融产品的交易量作为中间商的决策变量。
综上所述,本文的研究特色在于,在选题方面我们立足于低碳生产与低碳生活的国际总趋势,结合了国内碳交易环境,考虑了供应链上的低碳生产与碳交易过程;在建模方面,为更贴近实际,我们考虑了一个两层次的超网络供应链结构,同时创新地将碳交易中心引入到模型之中作为一个决策主体。所得结论不仅对供应链上的企业,还对碳交易中间机构的决策制定具有一定的参考价值;方法上我们所采用的变分不等式不仅在分析非线性问题中具有一定优势,且能描述出多个不同决策主体的博弈过程,并在一定条件下得到均衡解;另外,对于解的唯一性、存在性及最优解充要条件都给出了详细的证明。
2 供应链碳交易超网络模型
本文考虑一个由I个高排放供应商、J个低排放制造商、K个终端市场以及一个服务于I与J之间的碳交易中心组成的超网络模型,如图1所示。

图1 供应链碳交易超网络模型
图中实线为实体物流,虚线为信息流或资金流。有I+J+K∈V,V代表该区域内所有供应商、制造商及市场所组成的集合。生产交易过程中,供应商将产品供给制造商时将按某类既定的方式计量其产生的碳排放量。同时,制造商将其生产的产品销售给市场时也将产生一定的碳排放量。拥有碳排放量的两类企业可以到碳交易中心进行碳交易。我们假定碳交易中心会保证碳交易流平衡并控制碳交易产品的交易量。在进行生产之前,政府会对每一个参加交易的企业分配碳排放限额,当企业生产周期过后的碳排放量超过该配额时需要从碳市场上购买差额,相反则可出售差值。为简化分析,我们假设供应商碳排放量总是不低于政府分配限额,而制造商总的碳排放量不高于排放限额。高排放企业有如火力发电厂、铝厂等;低碳企业包括太阳能发电、风能发电业、部分服务行业等[21-22]。变分不等式应用于图1所示的超网络模型中描述的是参与人同时博弈的过程,即:供、需双方在做自己决策时还应考虑到竞争对手及上下游企业的决策[16]。在本文所述问题中,因同时考虑了企业与碳交易中心的决策过程,故企业在做决策时还应将碳交易中心的绩效纳入考虑范围[23]。
2.1 符号说明

2.2 供应商的优化条件
考虑竞争环境,供应商生产成本不仅与自己的产量相关,同时还与同级供应商的产量相关。生产成本函数为fi(Qi),其中Qi为IJ维向量。第i个供应商与第j个制造商的交易成本为cij(Qij),并假设生产成本与交易成本函数均为qij的连续可微凸函数;通过供给可获得收入ρijqij,产生碳排放量αijqij。已知供应商i需要向外部购买碳排放额tj,为此供应商将支付ρcti的代价。同时设碳市场上交易风险为ri=ri(ti)。因为本文仅考虑单个碳交易市场,在此省略下标为1的参数与变量。综上得供应商的利润最大化目标函数:
(1)
因为交易费用函数、风险函数等都是关于能源交易量的凸函数。(1)式关于q*ij的解也是下列变分不等式的解为:
(2)
其中ρ*ij为供应商与制造商达成的均衡价格,λij为保证(1)中第一个约束的拉格郎日系数。
2.3 制造商优化条件

制造商的交易风险为ri=ri(ti)。风险函数是关于制造商产量qjk的凸函数,且单调连续并可微。综上可得制造商总目标函数为:
(3)
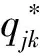
(4)
其中,ζ2j都是J维的拉格郎日系数向量。
2.4 市场行为

(5)

(6)
均衡状态下的变分不等式为:
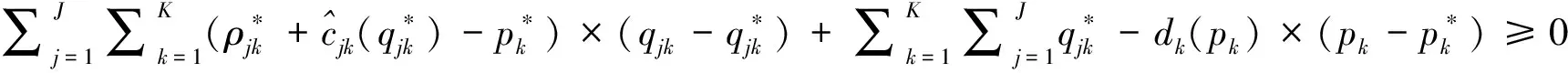
s.t.qjk≥0,pk≥0
(7)
2.5 碳交易中心最优化条件
交易中心里,碳排放供应源自制造商,需求汇往供应商。交易中心按固定比例对每笔交易收取交易费。已知供应商的碳排放需求量及制造商供给量分别为:
可知交易中心碳交易收益为:
(8)
对于一个金融产品的中介机构来说,交易过程中同样存在风险。设从制造商处流入的碳产品所造成的交易风险为:
(9)
交易中心将碳排放量出售给供应商时的风险为:
(10)

(11)

s.t.qij≥0,qjk≥0
(12)
λc为(11)式第一个约束相关的拉格郎日乘子。
2.6 供应链优化条件

s.t.K≡{(Q1,Q2,ρ1,ρ2,ρ3)|qij≥0,qjk≥0,ρij≥0,ρjk≥0,pk≥0,∀i,j,k}
(13)
其中,Q1为I×J维列向量,Q2为J×K维列向量;ρ1,ρ2,ρ3分别为向量及市场需求价格。
上述加总后的变分不等式均衡关系充要性的证明可参考Nagurney的研究。这里我们将式(2)、式(4)、(7)、(12)及式(13)解存在性的理论证明列于附录A。
(13)式可以简写成经典的变分不等式的标准形式:
[F(x*)T,x-x*]∀x∈K
(14)
其中X≡(Q1,Q2,ρ1,ρ2,ρ3),F(x*)示目标中出现的各个函数,(·,·)表示Eulidean空间上的内积。
2.7 解的存在条件
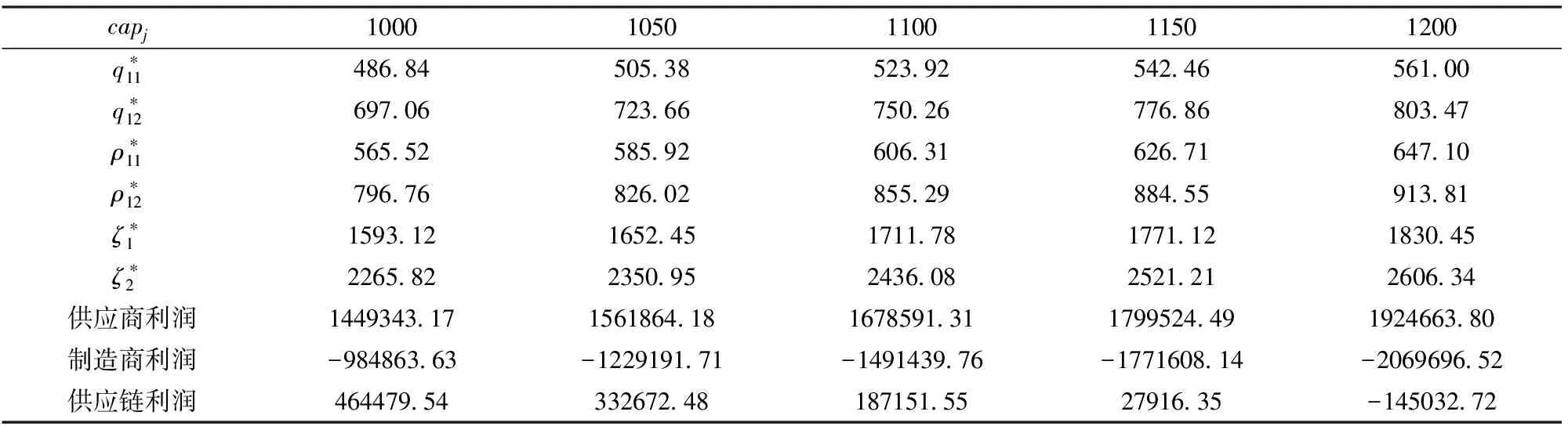
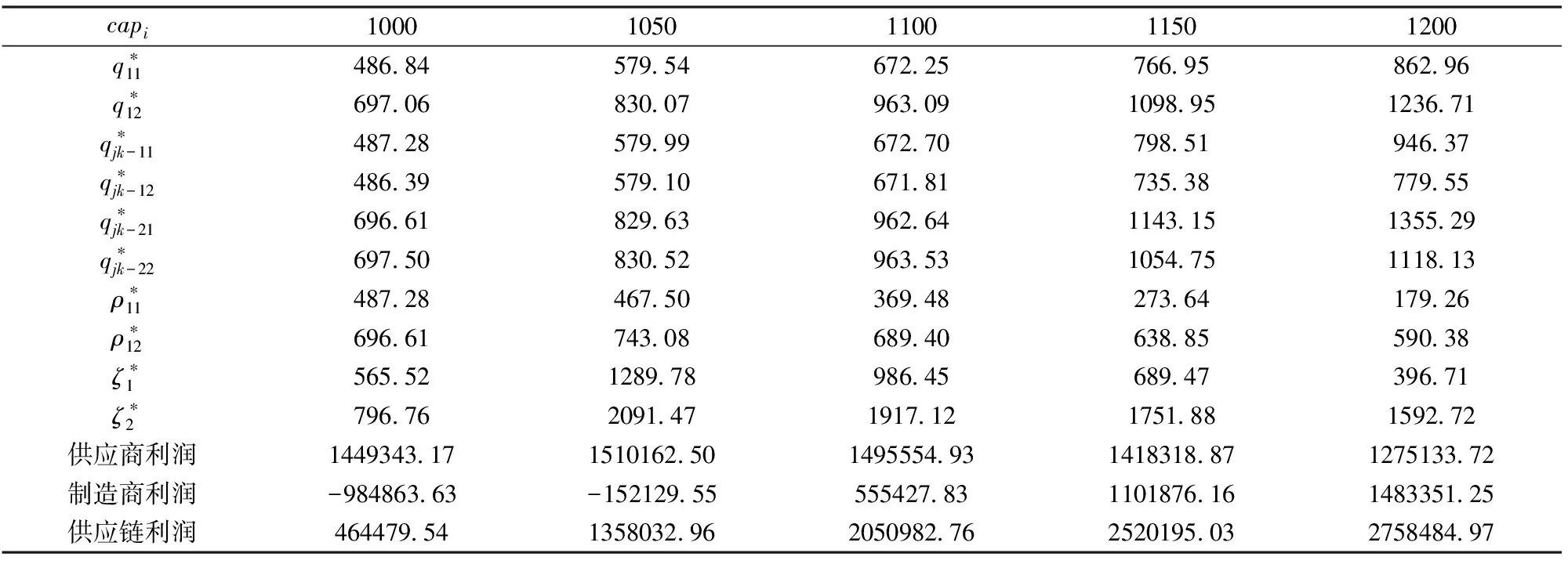
若变分不等式(13)的可行集是紧致有界的凸集,则可利用不动点定理等证明解的存在性。有界性自然源于本文的实际问题。不过即便无界,也可添加下列以z为半径的闭球Bz,并查看解是否存在于子集Kz=K∩Bz之中。如果解存在于Kz=K∩Bz之中,当且仅当|xz| 有界集中解的存在性证明见附录A,上述充要条件的证明可参考Stampacchia[26]定理1.4。其它关于解空间的凸性及解的有界性可参考Kinderlehrer与Stampacchia及Nagurney与Ke Ke[20]的研究。值得一提的是,在Stampacchia的研究中,关于无界集也可利用半径为R的球与凸集K相交取有界交集;另结合变分不等式的形式可知,若存在正常数M,N与R>0使得下式成立: 取Q1i,i={1,2,…,I}使得qij≥N,∀i,j (a) 取Q2i,i={1,2,…,I}使得∀ρ3,qjk≥N,∀j,k (b) 且有dk(pk)≤N, ∀ρ3与ρ3≥R,∀k (c) 可知原变分不等式(12)至少具有一个解,证明过程类似Nagurney与Zhao Lan[27]的定理3与命题1。 (d) (15) (16) 上述变分不等式问题解的严格单调性、唯一性及Lipschitz连续性见附录A,同时可参考文献[20]。 本文借用改进型投影算法验证模型的有效性。程序伪代码描述包含大量公式,因篇幅关系在此省略。具体内容,包括早期的投影算法可参考Bakusinskji与Polyak[28],Korpelevich[29]和Wang等[30]的研究。 这里我们构建一个由两个供应商,两个制造商,两个市场及一个碳交易中心组成的超网络模型,随后通过C++编程,基于所用算法进行了算例分析。网络结构见图2。 图2 碳交易超网络模型数据实例 由于条件限制,我们未能获得企业的真实数据,模型的具体形式根据实际问题并参考Nagurney的进行设定。 程序在159次迭代后结果收敛到一个点,通过该点可以得出最优的解向量信息。结果如表1所示。 结果显示,市场需求价格高出市场出清价格表明消费者在购买此类低碳产品时可以得到较多的消费者剩余。从利润来看,制造商表现欠佳,但较高的供应商利润使供应链整体利润保持在可接受的水平。这一点与结论1不谋而合。 现分析各变量及各方利润对碳配额的变化情况。固定其它参数不变改变制造商分配额,得表2。 表1 最优解及供应链各方决策 表2 对制造商碳排放配额敏感性分析 表3 对供应商碳排放配额敏感性分析 从上表2看出,当政府分配给制造商的碳排放额度上升时,供应链上各级企业将提升订货量且提升速度均匀,同时供应商的定价也随着市场出清价格的上升而上涨;制造商所获配额越高,其与供应商之间的利润差值越大,当配额放松到1200时,供应链整体利润不容乐观。可见,若政府过于放松对高排放企业的管制,将加剧供应链上各级企业间利润分配的两级化且对供应链整体利润产生负面影响。 保持其它参数不变,改变对供应商的碳分配额,得表3。 表3显示,当供应商所得配额上升时,将显著提升产量,降低产品价格。利润方面,不仅供应商与制造商利润分配差异不大,且供应链整体利润呈上升趋势。我们发现,此时供应商到制造商的订货量与制造商到市场的出货量都将提升。虽然价格下降了,但下降边际要小于产量的提升。同时,从公式(1)及假设易知,供应商配额的提升有助于降低其碳交易费用。这一现象说明,政府放松对高能耗供应企业碳排放量的管制不仅促进了消费,提升了供应链上的物流量,还有助于改善供应链整体的盈利情况。可见,面对高能耗型的供应商,政府需要在环境与利润之间做出权衡。 构建企业不参加碳交易体系时的变分不等式模型同样可参考(1)-(7)及(13)式的形式。沿用表2的数据,结果见表4。 与表1对比发现企业在未参加碳交易时各项数值均偏低;参加碳交易时供应商会将成本转嫁于制造商身上,结果使得供应商利润远大于制造商利润;双方不参加碳交易体系时制造商所获利润更大,但此时供应链总利润较大,且在不考虑碳交易时双方的订货量明显缩小。 本文利用变分不等式构建了一个由供应链子网及碳交易子网组成的超网络模型。探讨了供应商与制造商分别作为碳买家与卖家时的产品产量及定价决策。通过对多方博弈均衡的分析发现,最优供应价格随供应商的边际交易费用、边际碳交易量及碳交易边际风险的增加而递增。数值分析的结果表明碳交易环境下制造商的利润水平较差,但较高的供应商利润能维持供应链的整体水平。在给定相关企业最优决策的同时我们还找出了供应链成员之间利润分配情况与碳配额之间的关系。敏感性分析的结果表明,当政府放松对制造商排放的约束时,供应链上各级企业将提升订货量,同时供应商的定价也随着市场出清价格上升而上涨。但政府的这一举措可能导致供需双方利润的两极分化,同时对供应链整体利润产生消极影响。为此,政府可以针对高排放企业加紧排放管制;同时放松对低排放企业的要求。对比分析表明,供需双方企业在未参加碳交易时,给定其它条件不变,制造商订货量比参加碳交易时要小但所获利润较大,且供应链总体利润水平较高。 表4 最优解及供应链各方利润 附录 A 解的存在性、唯一性及充要条件 原问题(主要包括式(2)、(4)、(7)、(12)与(13))等价于下列表述: 存在性 充要条件 单调性 对于函数单调性,可令x1,x2∈K⊂Rn。根据凸性假设有f(x1)≥f(x2)+[f(x2),x1-x2]及f(x2)≥f(x1)+[f(x1),x2-x1]。两式相加可得[(F(x1)-F(x2))T,x1-x2]。显然,取严格不等号时函数严格单调。证毕。 对于解的唯一性,可假定x1≠x2为原方程两个解,代入上述两个方程得出与严格单调性相矛盾的结论,进而得证。 (感谢审稿人对该部分的要求,使本文更完整。证明过程有参考文献[26]与[28]。) 参考文献: [1] IPCC.Climate change 2007: Synthesis report[R], 2007. [2] Wang Jianzhou, Dong Yao, Wu Jie, et al.Coal production forecast and low carbon policies in China[J].Energy Policy, 2011, 39(10): 5970-5979. [3] Men Ming, Zhang Qiuli, Zhu Songge.Analysis and implications of China’s carbon trading[C].Proceedings of the IEEE International Conference on Automation and Logistics, Beijing: April 1-4, 2011. [4] Zhang Yuejun, Wei Yiming.An overview of current research on EU ETS: Evidence from its operating mechanism and economic effect[J].Applied Energy 2010, 87(6):1804-1814. [5] 中山大学法学院课题组.论中国碳交易市场的构建[J].江苏大学学报(社会科学版),2012, (1):70-76. [6] Du S, Ma F, Fu Z, et al.Game-theoretic analysis for an emission-dependent supply chain in a ′cap-and-trade′ system[J].Annals of Operations Research, 2011, doi: 10.1007/s10479-011-0964-6. [7] Diabat A, Simchi-Levi D.A carbon-capped supply chain network problem[C].Proceeding of Industrial Engineering and Engineering Management, Hong Kong, December 8-11,2009. [8] Chaabane A, Ramudhin A, Paquet M.Design of sustainable supply chains under the emission trading scheme[J].International Journal of Production Economics, 2012, 135(1):37-49. [9] Hugo A, Pistikopoulos E N.Environmentally conscious long-range planning and design of supply chain networks[J].Journal of Cleaner Production, 2005, 13(15):1471-1491. [10] Abdallah T, Farhat A, Diabat A, et al.Green supply chains with carbon trading and environmental sourcing: Formulation and life cycle assessment[J].Applied Mathematical Modelling, 2012,36(9):4271-4285. [11] Giarola S, Shah N, Bezzo F.A comprehensive approach to the design of ethanol supply chains including carbon trading effects[J].Bioresource Technology, 2012, (107):175-185. [12] Bojarski A D, Laínez J M, Espuna A, et al.Incorporating environmental impacts and regulations in a holistic supply chains modeling: An LCA approach[J].Computers and Chemical Engineering, 2009, 33(10): 1747-1759. [13] Wang Zhiping, Zhang Fumei, Wang Zhongtuo.Research on return supply chain supernetwork model based on variational inequalities[C].Proceedings of the IEEE International Conference on Automation and Logistics, Jinan, August 18 - 21, 2007. [14] 王志平,王众托.超网络理论及其应用[M].北京:科学出版社,2008. [15] Sheffi Y.Urban transportation networks: Equilibrium analysis with mathematical programming methods[M].NJ: Printice-Hall, 1985. [16] Nagurney A, Dong J.Supernetworks: Decision-making for the information age[M].Cheltenham: Edward Elgar Publishing, 2002. [17] Wu Kai, Nagurney A, Liu Zugang , et al.Modeling generator power plant portfolios and pollution taxes in electric power supply chain networks: A transportation network equilibrium transformation[J].Transportation Research Part D,2006, 11(3): 171-190. [18] Nagurney A, Liu Zugang, Woolley T.Optimal endogenous carbon taxes for electric power supply chains with power plants[J].Mathematical and Computer Modelling, 2006, 44(9): 899-916. [19] Nagurney A, Cruz J.International financial networks with intermediation: Modeling, analysis, and computations[J].Computational Management Science 2003, (1): 31-58. [20] Nagurney A, Ke K.Financial networks with intermediation: Risk management with variable weights[J].European Journal of Operational Research,2006, 172(1): 40-63. [21] 朱庆华,窦一杰.基于政府补贴分析的绿色供应链管理博弈模型[J].管理科学学报,2011, (6):86-95. [22] 杨家威.低碳经济中政府补贴的博弈分析[J].商业研究,2010, (8): 109-112. [23] Nagurney A, Dong J, Zhang Ding.A supply chain network equilibrium model[J].Transportation Research Part E, 2002, (38): 281-303. [24] 娄伟,李萌.低碳经济规划:理论·方法·模型[M].北京:社会科学文献出版社,2011. [25] Koopmans T C.Optimum utilization of the transportation systems[J].Econometrica,1949,(17):136-146. [26] Kinderlehrer D, Stampacchia G.An introduction to variational inequalities and their applications[M].New York: Academic Press, 1980. [27] Nagurney A, Zhao Lan.Networks and variational inequalities in the formulation and computation of market disequilibria: The case of direct demand functions[J].Transportation Science, 1993,27(1): 4-15. [28] Bakusinskji A B, Polyak B T.On the solution of variational inequalities[J].Soviet Mathematics Doklady, 1974 (15): 1705-1710. [29] Korpelevich G M.The extragradient method for finding saddle points and other problems[J].Matekon 1976, (13): 35-49. [30] Wang Y J, Xiu N H, Zhang J Z.Modified extragradient method for variational inequalities and verification of solution existence[J].Journal Of Optimization Theory And Applications, 2003, 119(1): 167-183. [31] Nagurney A, Dong J, Hughes M.Formulation and computation of general financial equilibrium[J].Optimization, 1992, 26(3-4): 339-354. [32] Nagurney A, Toyasakin F.Reverse supply chain management and electronic waste recycling: A multitiered network equilibrium framework for E-cycling[J].Transportation Research Part E, 2005, 41(1): 1-28.

2.8 企业最优定价

3 数值例子
3.1 超网络模型算例

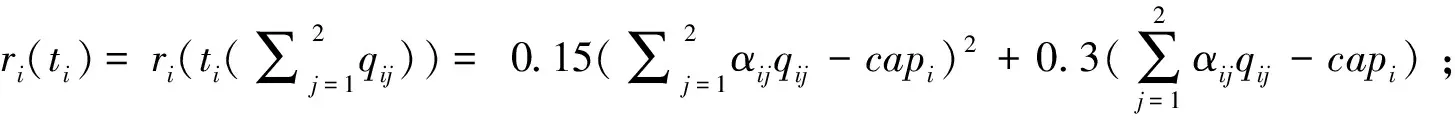
3.2 算例结果
3.3 敏感性分析

3.4 对比分析
4 结语