投资偏好与“特质波动率之谜”——以中国股票市场A股为研究对象

刘维奇，邢红卫，张信东,

(1.山西大学管理与决策研究所，山西 太原 030006；2.山西大学经济与管理学院，山西 太原 030006)

1 引言

自1990年11月26日上海证券交易所成立以来，我国股票市场发展已历经二十余年。然而，我国股票市场近年来频繁的暴涨暴跌现象，以及明显高于全球其它股市的换手率和市盈率，都说明我国投资者的投机心理依然很强。传统金融学理论假设投资者都是理性和风险厌恶的，对资产没有选择性的偏好，然而大量研究表明并非如此。投资偏好是投资者由于环境、学识、财力、投资时机等因素的不同，导致投资风险的承受能力不同，从而对资产产生不同的喜好程度，并据此进行资产优先排序及数量组合，比如本土情结[1]、小盘股效应[2]、归属感投资[3]、社会责任性投资偏好[4-5]、彩票性投资偏好[6-7]等。

与价格走势平平的股票相比，投资者也更喜欢选择价格变化幅度较大的股票，即过去某段时期内股票价格由较低的水平迅速上涨到较高的水平，或者由较高的水平骤然下降到较低的水平。股票价格在短期内由低到高变化会给投资者乐观的心理暗示，股票在未来会涨到更高的价格，投资此类股票会获得较高的超额回报。而股票价格在短期内由高到低变化也会给投资者某种心理暗示，可能“触底反弹”的抄底机会来临了，投资此类股票也会获得较高的超额回报。因此，投资者在进行投资决策时，更加愿意选择过去价格变化幅度较大的股票，或者说价格极差较大的股票，以实现低价买进，高价卖出的交易策略，得到额外的报酬。

股票价格在过去某段时期内变化幅度较大，表明其偏离真实价值的程度较大。究其原因，是由于过去某段时期内这类股票的流动性较差，价格反映股票信息的能力不足，而价格的大幅变化也使这类股票具有较高的特质波动率(idiosyncratic volatility，IV)。由无套利定价原理，投资者对这类股票的大量投资和频繁交易会降低其未来收益，这就可能使特质波动率与预期收益之间产生负向关系，即产生了股票市场的“特质波动率之谜(idiosyncratic volatility puzzle)”，这正是本文所要探讨的主题。

股票市场中是否存在“特质波动率之谜”？存在“特质波动率之谜”的原因是什么？这是资本资产定价领域中亟待解决的问题。资本资产定价模型(capital asset pricing model，CAPM)建立在理性投资者和无摩擦市场的假设之下，认为只有系统性风险决定股票的预期收益，公司层面的特质风险可以通过分散化投资被消除，并且建立了预期收益与市场风险之间的线性模型，即证券市场线(SML)。Levy[8]表明如果投资者持有的组合不包含足够多的股票，特质波动率将影响股票的均衡价格。Merton[9]提出在信息不完全的资本市场均衡模型下，具有高特质波动率的股票未来应该有高的平均收益，以此来补偿投资者未持有足够分散化组合所带来的风险。研究证据也表明，实际中绝大多数个人投资者都不能持有足够分散化的投资组合[10-11]。Ang等[12]以Fama-French三因子模型[13]回归残差序列的标准差度量特质波动率，不仅发现特质波动率与股票预期收益之间有显著关系，而且是负向关系，“高特质波动率组合未来有低收益，低特质波动率组合未来有高收益”，并且市场波动风险、流动性、动量、偏度和杠杆等因素都不能解释这一现象。传统的金融风险收益理念认为高风险伴有高收益的风险补偿，因此如果特质风险无法通过分散投资被完全规避，即其假定前提无法实现会产生风险溢价时，其与股票收益之间的关系也应当是正向关系。特质风险与收益之间的负向关系有悖于“高风险有高收益”的金融风险定价逻辑，因此产生了特质波动率异象，也被称为“特质波动率之谜”。

关于“特质波动率之谜”的检验与分析，目前已是实证资本资产定价领域的热点问题之一。Bali和Cakici[14]从度量特质波动率的方法、数据频率、形成组合的分组方式、组合收益的加权方式、样本区间和数据库等技术角度检验“特质波动率之谜”存在的稳定性。Jiang等[15]研究了特质波动率、公司未来的利润冲击、股票预期收益三者之间的关系，发现特质波动率与公司未来的利润冲击及股票预期收益均为负向关系，并且特质波动率对收益的预测能力由其包含的与未来利润相关的信息决定，“特质波动率之谜”由公司选择性地披露经营信息引起，同时在噪声交易者关注的股票中更为明显。Han和Kumar[16]的研究也表明，“特质波动率之谜”主要集中于个人投资者选择的股票。杨华蔚和韩立岩[17]、左浩苗等[18]以反映投资者异质信念的换手率来分析“特质波动率之谜”。Huang Wei等[19]以收益的短期反转现象来分析“特质波动率之谜”，认为月收益的一阶负自相关可能导致了特质波动率与预期收益之间的负向关系。Bali等[7]以投资者喜欢像彩票类股票的实际为依据，发现过去一个月的最大日收益率(MAX)和股票预期收益有显著负向关系，若以最大日收益率作为控制变量，将反转Ang等[8]的研究结论，即特质波动率与预期收益之间的负向关系变为正。Chabi-Yo[20]以随机贴现因子解释特质波动率溢价的来源，在控制了非系统协偏度因子后，特质波动率和预期收益之间不再存在显著关系。

基于以上文献，本文首先研究特质波动率与股票预期收益的关系，检验中国股票市场是否存在“特质波动率之谜”。尽管当前已有针对这一工作的研究成果，如黄波等[21]，杨华蔚和韩立岩[17]，徐小君[22]，左浩苗等[18]，邓雪春和郑振龙[23]等，然而由于估计特质波动率的方法和研究样本区间不同，我们有必要对中国股票市场“特质波动率之谜”的存在性进行再次论证。其次，在中国股票市场存在“特质波动率之谜”的基础上，进行稳健性检验，考察动量、规模、流动性、换手率，短期反转、最大日收益率等指标对“特质波动率之谜”的影响。再次，从投资偏好出发，分析投资者选择过去某段时期内价格变化幅度较大的股票这一偏好是否是造成“特质波动率之谜”的原因，即分析价格极差对“特质波动率之谜”的解释能力。我们的研究不仅是对现有文献的补充，而且结合股票市场投资者投机心理较强，喜欢价格变化幅度较大的股票的事实，进一步提高对“特质波动率之谜”成因的理解。

2 理论模型与方法

2.1 度量特质波动率

首先，我们度量公司特质风险的代理指标——特质波动率。按照Malkiel和Xu Yexiao[24]的方法，回归估计CAPM模型：

Ri,t-rt=αi+βi(Rm,t-rt)+εi,t

(1)

(2)

2.2 形成组合的加权方式

对于形成组合的加权方式，当前主要以市值加权(value-weighted，VW)、等权(equal-weighted，EW)和毛收益加权(gross return-weighed，RW)为主。如果股票市场存在规模效应，小规模股票会较大规模股票有更高的收益率，等权计算组合收益会放大小规模个股的收益率在组合中的比重，对检验组合收益率与特质波动率的关系造成一定程度的偏差。而以毛收益加权被证明能有效消除组合收益率中微观结构带来的偏差[25]。因此在本文的组合分析中，我们以市值加权(VW)、等权(EW)和毛收益加权(RW)三种方式计算组合收益率，进行比对分析。

2.3 变量说明

为了检验中国股票市场“特质波动率之谜”存在与否的稳定性，我们引入以下控制变量。

(1)规模(SIZE)：以公司总市值的自然对数作为规模的测量指标。

(2)交易量(VOL)：以交易金额的自然对数作为交易量的测量指标。

(3)流动性指标(liquidity, LIQ)：梁丽珍和孔东民[26]研究表明Pastor和Stambaugh[27]的流动性测度比较适合于大规模公司，在中国股票市场Amihud[28]的测度优于其它测度。因此本文选择Amihud[28]测度作为衡量流动性的指标。Amihud[28]测度实际衡量的是股票的非流动性，具体来说，股票i在第t日的非流动性为：

其中，Ri,t和Vi,t分别是股票i在第t日的收益率和交易金额，Daysi,t是股票i从当月第一个有效交易日到第t日的有效交易天数。Amihud流动性测度越大，表明股票的流动性越差，流动性风险越大，则股票要求的流动性风险溢价就越高。

(4)动量(momentum, MOM)：动量最初由Jegadeesh和Titman[29]提出，表示历史累积收益对当前收益的影响。Jegadeesh和Titman[29]的研究表明，历史低收益股票在未来继续有低收益，而低收益股票一般有较高的波动性。在本文的研究中，按照Jegadeesh和Titman[29]的定义，以股票t-3月和t-2月的累积收益作为个股第t月动量的测量指标。

(5)短期反转(short-term reversal, REV)：依据Jegadeesh[30]所表明的，股票在当月的收益翻转由上个月的月收益代替。如果个股月收益率序列具有一阶负自相关系数，则意味着收益存在短期反转。若同时在个股月收益与当月特质波动率之间存在正向关系，则收益短期反转就能够解释特质波动率与预期收益之间的负向关系，即“特质波动率之谜”。

(6)换手率(turnover, TUR)：杨华蔚和韩立岩[17]、左浩苗等[18]的研究表明，投资者异质信念可能是造成“特质波动率之谜”的原因。按照Boehme等[31]的建议，本文选择股票的换手率作为异质信念的代理变量，并且以个股成交金额与流通市值的比值作为换手率的测量指标。

(7)最大日收益率(maximum of returns, MAX)：Bali等[7]以个股月内最大日收益作为控制变量，检验了美国股票市场“特质波动率之谜”的稳定性。为此，本文也检验个股月内最大日收益率对特质波动率与股票收益之间关系的影响。

(8)价格极差(range of prices，RP)：在套利机会的驱使下，投资者都渴望在股票价格较低的时候买进，在股票价格较高的时候卖出，因此更倾向于投资过去价格变化幅度较大的股票。个股月内的价格极差反映了月内股票价格的最大变化幅度，而价格的大幅变化也表明了股票所蕴含的风险。在本文，我们以个股每日收盘价作为其每日的价格，以月内最大日收盘价与最小日收盘价之差作为当月的价格极差，并分析其对“特质波动率之谜”的解释能力。

3 实证结果

3.1 样本选取

本文选择中国沪深两市A股所有股票作为研究对象。由于沪深两市自1996年12月16日开始实行涨停盘制度，这种交易制度的施行会对股票收益的变化产生较大影响，因此本文的样本期选择从1997年1月2日至2011年12月31日，股票数据来自国泰安CSMAR金融数据库，剔除其中的创业板和上市时间过短的股票数据，计算Fama-French三因子模型所需的公司账面价值信息和日无风险收益率来自锐思金融研究数据库。此外，由于中国股票市场在1999年2月份的交易日只有7天，为了确保每个月有足够多的日度数据进行CAPM模型和Fama-French三因子模型拟合，以及个股特质波动率的连续时间序列特征，我们剔除月内交易天数小于7的当月股票数据。

3.2 “特质波动率之谜”存在性检验

我们先以投资组合分析方法检验中国股票市场“特质波动率之谜”的存在性。投资组合分析法是根据某一指标构建不同的投资组合，检验不同组合在持有期的收益率是否存在显著差异。

在表1的Panel A，以股票的月内日数据估计CAPM模型，得到个股每个月的特质波动率，在每个月以特质波动率从低到高对股票进行排序，按分位点将所有股票分成5个组合，以流通市值加权计算组合当月的特质波动率。按照1/0/1交易策略持有组合一个月，分别计算以流通市值加权、平均加权和毛收益加权的组合收益率。Panel A的第二列展示了流通市值加权组合特质波动率的时间序列平均值。流通市值加权组合特质波动率的最低值是1.1182%，最高值是3.1916%。第三到第五列分别展示了以流通市值加权、平均加权和毛收益加权的组合预期收益率的时间序列平均值，以特质波动率从低到高形成组合的预期收益率基本都显示了从高到低的趋势，收益率最高的是特质波动率第二低的组合。高低特质波动率组合的收益率之间存在显著差异，以FF-3因子模型调整系统性风险后的截距项差值为负，且Newey-West[32]统计检验(括号内)显著不为零。以流通市值加权计算的组合收益率为例，低特质波动率组合的预期收益率为1.1335%，高特质波动率组合的预期收益率为0.5172%，高低特质波动率组合的预期收益率之差为-0.6163%，对应的显著性检验Newey-West-t值为-5.2104，以FF-3因子模型调整系统性风险后的截距项差值为-0.5054%，对应的显著性检验Newey-West-t值为-5.0311。与流通市值加权相比，以毛收益加权进一步增大了高低特质波动率组合预期收益率之间的差值(由-0.6163%变为为-1.3645%)和FF-3因子模型回归的截距项差值(由-0.5054%变为为-1.2430%)。不同的加权方式都表明，组合的特质波动率与预期收益率之间存在显著负向关系。

在表1的Panel B，采用Fama-French三因子模型估计股票的特质波动率，在每个月以个股特质波动率从低到高排序形成组合，以同样的1/0/1交易策略持有组合一个月，计算组合特质波动率和预期收益率的时间序列平均值。第二列流通市值加权组合低特质波动率的值是0.9590%，高特质波动率的值是2.8717%，都低于CAPM模型估计的结果，这也与模型本身的设定相一致。第三到第五列以三种方式加权得到的组合预期收益率基本都显示了从高到低的趋势，高低特质波动率组合的预期收益率存在显著差异，以FF-3因子模型调整后的截距项差值为负，且显著不为零。以流通市值加权计算的组合收益率为例，低特质波动率组合的预期收益率为1.2065%，高特质波动率组合的预期收益率为0.4711%，高低特质波动率组合的预期收益率之差为-0.7354%，对应的显著性检验Newey-West-t值为-5.9830，以FF-3因子模型调整系统性风险后的截距项差值为-0.6360%，对应的Newey-West-t值为-5.7420。以毛收益加权计算组合的预期收益率，更为明显地增大了高低特质波动率组合预期收益率之间的差值(由-0.7354%变为-1.4772%)和FF-3因子模型回归的截距项差值(由-0.6360%变为-1.3517%)。不同的加权方式都表明，组合的特质波动率与预期收益率之间存在显著负向关系，即存在“特质波动率之谜”。

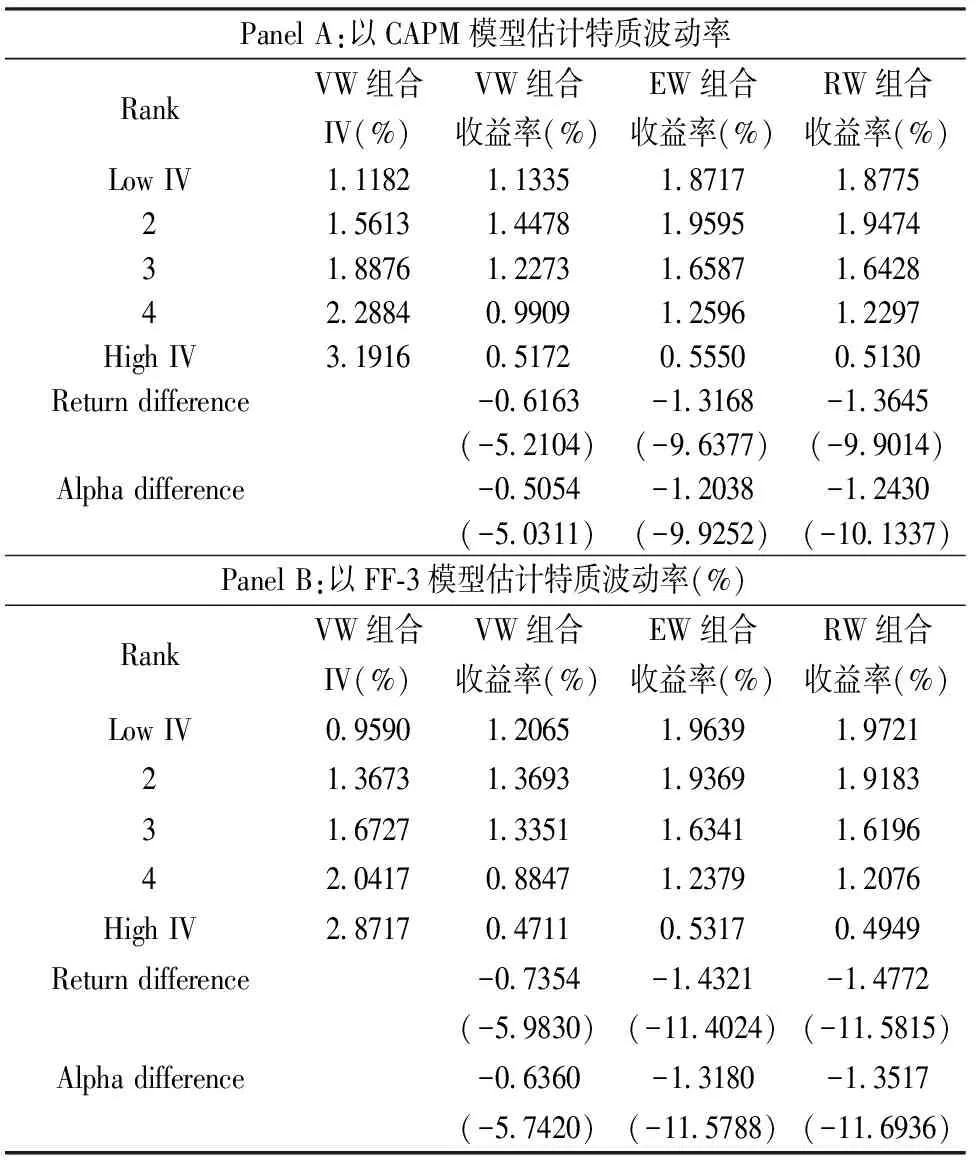
表1 组合特质波动率及其收益率

由表1，低特质波动率组合与高特质波率组合相比，每年至少有6%的超额收益率。

3.3 稳健性检验

我们用二维投资组合分析方法检验“特质波动率之谜”的稳定性，即先以控制变量对股票进行分组，在每一个组合内再以特质波动率对股票进行分组，构建二维的投资组合，控制其它因素的影响后，检验不同特质波动率组合在持有期的收益率是否存在显著差异，具体结果见表2。

首先，为了检验股票规模对“特质波动率之谜”的影响，在每个月先以规模从低到高排序，将所有股票按五分位点分成5个组合。在每个组合内再以Fama-French三因子模型计算的特质波动率从低到高排序，按五分位数将股票进行分组，形成5×5个收益组合，持有组合一个月并计算其收益率。在5个规模分位组上对其收益率进行算术平均，这样不论规模较大的股票还是规模较小的股票，都被平均分配到按特质波动率排序形成的组合里，即规模效应对高低特质波动率组合之间收益差异的影响被消除。Panel A的第二列展示了控制规模因素的影响后，从低到高特质波动率组合流通市值加权收益率在样本期内的时间序列平均值，显示了从高到低的趋势。低特质波动率组合的收益率是1.9732%，高特质波动率组合的收益率是0.5226%，高低特质波动率组合的收益率差值是-1.4506%，对应的显著性检验Newey-West-t值为-11.6344。通过Fama-French三因子模型调整系统性风险后的截距项的差值是-1.2983%，对应的显著性检验Newey-West-t值为-11.7854。Panel B和Panel C的第二列分别展示了控制规模因素影响后，平均加权组合收益率的时间序列平均值和毛收益加权组合收益率的时间序列平均值。两种加权方式的低特质波动率组合的收益率分别是2.0936%和2.0933%，高特质波动率组合的收益率分别是0.5264%和0.4939%，高低特质波动率组合的预期收益率的差值分别是-1.5672%和-1.5994%，对应的显著性Newey-West-t值分别为-11.9144和-11.9496。通过Fama-French三因子模型调整系统性风险的截距项的差值分别是-1.4246%和-1.4507%，对应的显著性检验Newey-West-t值分别为-11.6459和-11.2801。控制规模因素对组合收益率的影响后，特质波动率与预期收益之间依然存在稳定的负向关系。

收益的中期动量对“特质波动率之谜”是否有影响？依据Jegadeesh和Titman[25]计算3个月动量指标对数据的要求，先剔除连续交易时间少于3个月的股票。与检验规模因素对“特质波动率之谜”的方法一样，在每个月先以3个月动量指标从低到高排序，将所有股票按五分位点分成5个组合，在每个组合内再以Fama-French三因子模型计算的特质波动率从低到高排序，按五分位数将股票进行分组，形成5×5个收益组合，持有组合一个月并计算收益率。在5个动量分位组上对其收益率进行算术平均，控制动量因素的影响后构建特质波动率从低到高的5个组合。Panel A、Panel B和Panel C的第三列分别展示了控制中期动量影响后，流通市值加权组合收益率的时间序列平均值、平均加权组合收益率的时间序列平均值和毛收益加权组合收益率的时间序列平均值。低特质波动率组合未来有高收益，三种加权方式的结果分别为1.4621%，2.0776%，2.0840%，高特质波动率组合未来有低收益，三种加权方式的结果分别为0.4388%，0.5166%，0.4842%，高低特质波动率组合的预期收益率之间存在显著差异，三种加权方式的组合预期收益率的差值分别是-1.0233%，-1.5610%，-1.5998%，且Newey-West-t统计检验显著。经Fama-French三因子模型调整系统性风险后，高低特质波动率组合未来依然存在显著的风险溢价差异，回归三种加权方式组合收益率的截距项差值分别是-0.9343%，-1.4517%，-1.4795%，Newey-West-t统计检验显著。

Huang Wei等[19]以美国股票市场作为研究对象，认为月收益的短期反转对“特质波动率之谜”具有一定的解释能力，那么在中国股票市场是否如此呢？在每个月先以上个月月收益从低到高将股票分成5个组合，在每个组合内再以Fama-French三因子模型计算的特质波动率从低到高将股票进行分组，形成5×5个收益组合，持有组合一个月并计算收益率。在上个月月收益的分位组上对其收益率进行算术平均，控制收益短期反转的影响后构建特质波动率从低到高5个组合。Panel A、Panel B和Panel C的第四列分别展示了控制短期反转影响后，流通市值加权组合收益率的时间序列平均值、平均加权组合收益率的时间序列平均值和毛收益加权组合收益率的时间序列平均值。低特质波动率组合未来有高收益，高特质波动率组合未来有低收益，高低特质波动率组合的预期收益率之间存在显著差异，经Fama-French三因子模型调整系统性风险后，高低特质波动率组合未来依然存在显著的风险溢价差异。

Spiegel和Wang Xiaotong[33]的研究表明，特质波动率较流动性指标对股票收益有更强的影响力，能够涵盖流动性对股票收益的解释能力，并且特质波动率与Amihud[28]的流动性指标负相关，那么在中国股票市场流动性是否依然无法解释“特质波动率之谜”呢？为此，先以Amihud[28]的流动性指标构建组合，在组合内再以Fama-French三因子模型计算的特质波动率构建组合，形成5×5二维投资组合。Panel A、Panel B和Panel C的第五列分别展示了控制流动性影响后，流通市值加权组合收益率的时间序列平均值、平均加权组合收益率的时间序列平均值和毛收益加权组合收益率的时间序列平均值。低特质波动率组合未来有高收益，高特质波动率组合未来有低收益，高低特质波动率组合的预期收益率之间存在显著差异，经Fama-French三因子模型调整系统性风险后，高低特质波动率组合未来依然存在显著的风险溢价差异，控制流动性对组合收益的影响后依然存在“特质波动率之谜”。

鉴于与杨华蔚和韩立岩[17]、左浩苗等[18]研究所用的样本期不同，我们也检验了换手率对“特质波动率之谜”的影响。在Panel A、Panel B和Panel C的第六列构建5×5二维投资组合，发现控制换手率对组合收益的影响后，高低特质波动率组合预期收益率的差值较表1中Panel B的结果有一定程度降低，流通市值加权、平均加权和毛收益加权的结果分别为-0.4673%，-0.7495%，-0.7876%，然而Newey-West-t统计检验显著。经Fama-French三因子模型调整系统性风险后，截距项的差值也有所降低，三种加权方式的结果分别为-0.3740%，-0.6364%，-0.6651%，且Newey-West-t统计检验显著。由此可见，反映投资者异质信念的换手率对“特质波动率之谜”具有一定程度的解释能力，然而特质波动率与预期收益之间的负向关系依然显著，这与杨华蔚和韩立岩[17]、左浩苗等[18]的研究结论相一致。

Bali等[7]以美国股票市场作为研究对象，发现月内最大日收益率是特质波动率的替代指标，将月内最大日收益率作为控制变量后，特质波动率与预期收益之间的负向关系被反转为正。在Panel A、Panel B和Panel C的第七列，我们以月内最大日收益率作为控制变量构建5×5二维投资组合。控制最大日收益率后，与表1中Panel B的结果相比，高低特质波动率组合预期收益率的差值也有一定程度降低，流通市值加权、平均加权和毛收益加权的结果分别为-0.6611%，-1.0280%，-1.0537%，Newey-West-t统计检验都显著。经Fama-French三因子模型调整系统性风险后，截距项的差值也有所降低，三种加权方式的结果分别为-0.6134%，-0.9662%，-0.9905%，且Newey-West-t统计检验显著。由高低特质波动率组合收益率差及Fama-French三因子模型截距项差，最大日收益率也可以在一定程度上解释但不能完全解释“特质波动率之谜”，这不同于Bali等[7]以美国股票市场作为研究对象得到的结论。

由表2的结果，与控制规模、动量、收益短期反转、非流动性等指标后相比，分别控制换手率和月内最大日收益率后，高低特质波动率组合的收益率差幅度都有明显降低，表明换手率和月内最大日收益率都对“特质波动率之谜”有一定程度的解释能力，然而并不能完全解释特质波动率与预期收益之间的负向关系，“特质波动率之谜”依然统计显著。

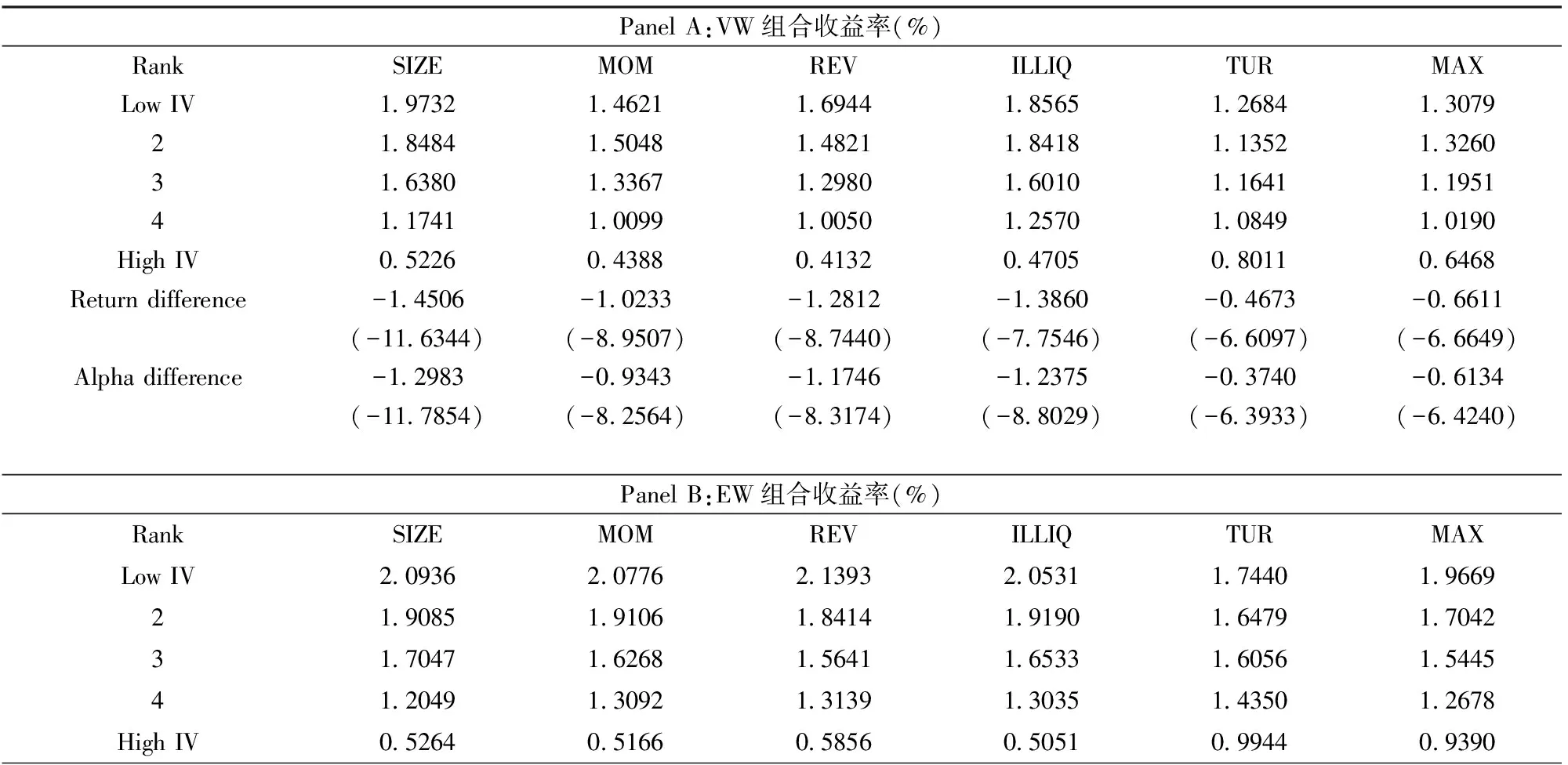
表2 控制其它变量后组合收益率

续表2

3.4 价格极差对“特质波动率之谜”的解释

与选择价格曲线平平的股票相比，投资者更愿意选择过去价格变化幅度较大，即价格极差较大的股票，以实现低价买进，高价卖出的交易策略，获得超额收益。在某段时期内价格变化幅度较大的股票特质波动率也较大，投资者对这类股票的大量投资将会使其未来收益偏低，产生了有悖于金融风险定价逻辑的“特质波动率之谜”——高(低)特质波动率股票有低(高)预期收益。那么，是否由于投资者的这种投资偏好导致了“特质波动率之谜”呢？我们以月内日收盘价极差作为控制变量，构建二维投资组合，分析月内日收盘价极差对“特质波动率之谜”的解释能力。

在表3，先以月内日收盘价极差从低到高排序，将所有股票按五分位点分成5个组合。在每个组合内再以Fama-French三因子模型计算的特质波动率从低到高排序，按五分位数将股票进行分组，构建5×5个收益组合，持有组合一个月并计算其收益率，并计算组合收益率在样本期内的时间序列平均值。在收益率极差分位组上对其收益率进行算术平均，控制收益率极差的影响后构建特质波动率从低到高的5个组合。表3的第二列以流通市值加权计算组合收益率，高低特质波动率组合收益率的差值依然显著为负，且为-0.4640%，Newey-West-t检验值(括号内)为-6.0788，与表1中Panel B第三列高低特质波动率组合收益率的差值相比，明显有所降低。以Fama-French三因子模型调整组合的系统性风险，截距项的差值是-0.4482%，Newey-West-t检验值为-10.9511。分别以平均加权和毛收益加权计算组合收益率，高低特质波动率组合收益率的差值及经Fama-French三因子模型调整后截距项的差值都较表1中Panel B的结果有所降低。

由表3，以月内日收盘价极差作为控制变量，特质波动率与股票预期收益之间的负向关系依然显著，然而高低特质波动率组合的溢价差异有不同程度降低，这意味着价格极差对特质波动率与股票预期收益之间的负向关系有一定的解释能力，投资者偏好投资价格极差较大的股票可能是产生“特质波动率之谜”的部分原因。

表3 控制价格极差后组合收益率

3.5 横截面回归分析

在进行横截面回归分析之前，为了认识横截面上特质波动率与其它控制变量之间的相关性，先进行横截面相关性分析。在每个月计算以Fama-French三因子模型得到的股票特质波动率序列与其它控制变量序列之间的相关系数，再计算其在时间序列上的平均值，结果见表4。特质波动率(IV)与价格极差(RP)、最大日收益率(MAX)、换手率(TUR)之间都有较高的横截面相关系数，分别为0.4317，0.6979和0.5451。价格极差(RP)与交易量(VOL)和换手率(TUR)之间的横截面相关系数分别为0.2131和0.3576，表明价格极差较高的股票交易量和换手率也较高，而个股的交易量和换手率基本上可以反映投资者对其的偏好程度，由此说明投资者对价格极差较高的股票有一定程度的投资偏好，验证了我们的理论假设。

以Fama-MacBeth[34]回归方法，进一步检验特质波动率和预期收益在横截面上的关系。横截面回归分析与投资组合分析的不同之处在于，横截面回归分析需要给出预期收益与特质波动率及其它控制变量之间的函数关系式，当然，投资组合分析也难以反映各变量在横截面上的信息，也无法同时控制多个变量对收益的影响。为了同时检验其它多个控制变量对特质波动率与预期收益之间关系的影响，我们在横截面上以特质波动率(IV)、价格极差(RP)、最大日收益率(MAX)、规模(SIZE)、交易量(VOL)、动量(MOM)、收益反转(REV)、流动性(ILLIQ)和换手率(TUR)作为自变量，对下个月月收益进行回归，并分析回归系数在时间序列上的显著性(1%水平下)。为了减小不同指标量纲对回归结果的影响，回归前对每个横截面上所有指标数据进行标准化处理。具体来说，在每个月，以各变量标准化后的月度数据进行以下线性回归分析，

Ri,t+1=λ0,t+λ1,tIVi,t+λ2,tRPi,t+λ3,tMAXi,t+λ4,tSIZEi,t+λ5,tVOLi,t+λ6,tMOMi,t+λ7,tREVi,t+λ8,tILLIQi,t+λ9,tTURi,t+εi,t+1

(3)

计算所有月回归系数的平均值及其Newey-West-t值。表5列出了从1997年1月至2011年12月回归系数的均值，括号内为相应的Newey-West-t检验值。

在单个自变量回归模型中，特质波动率回归系数的平均值为-0.0529，Newey-West-t检验值为-7.3455。由于横截面回归意味着对每一个回归样本都赋予了相等权重，因此表明以平均加权计算组合收益，特质波动率与预期收益之间存在显著的负向关系，进一步验证了“特质波动率之谜”的存在性。以价格极差作为自变量对下个月收益进行回归，回归系数在时间序列上的平均值分别为-0.0230，Newey-West-t检验值分别为-3.4586，说明价格极差与预期收益之间也存在显著的负向关系。由于最大日收益率与特质波动率之间、换手率与特质波动率之间也存在较强的相关性，因此再分别以最大日收益和换手率作为单变量对下月收益进行回归，回归系数也显著为负。

在多个自变量回归模型中，若以特质波动率和价格极差同时作为自变量，回归系数的时间序列平均值分别为-0.0527和-0.0044，相应的Newey-West-t检验值为-4.4171和-1.3589，虽然特质波动率的系数依然显著为负，然而其Newey-West-t检验值明显较单变量时有所降低。若以最大日收益或换手率作为特质波动率之外的第二个自变量进行回归，特质波动率的系数依然显著为负，其Newey-West-t检验值也明显较单变量时有所降低。由此，虽然在统计学和金融学上，价格极差、最大日收益率、换手率都与特质波动率之间有较强的相关性，然而都只可以在一定程度上解释“特质波动率之谜”，但不能完全解释“特质波动率之谜”。鉴于此，我们将价格极差、最大日收益率、换手率和特质波动率同时作为自变量对下月收益进行回归，特质波动率系数的Newey-West-t检验值为-1.7074，表明特质波动率与预期收益之间不存在显著关系。如果继续加入其它控制变量，以特质波动率、价格极差、最大日收益率、规模、交易量、动量、收益反转、流动性和换手率同时作为自变量对下月收益回归，特质波动率的系数又显著为负。由此，价格极差、最大日收益率和换手率的共同作用可能是造成“特质波动率之谜”的主要原因。

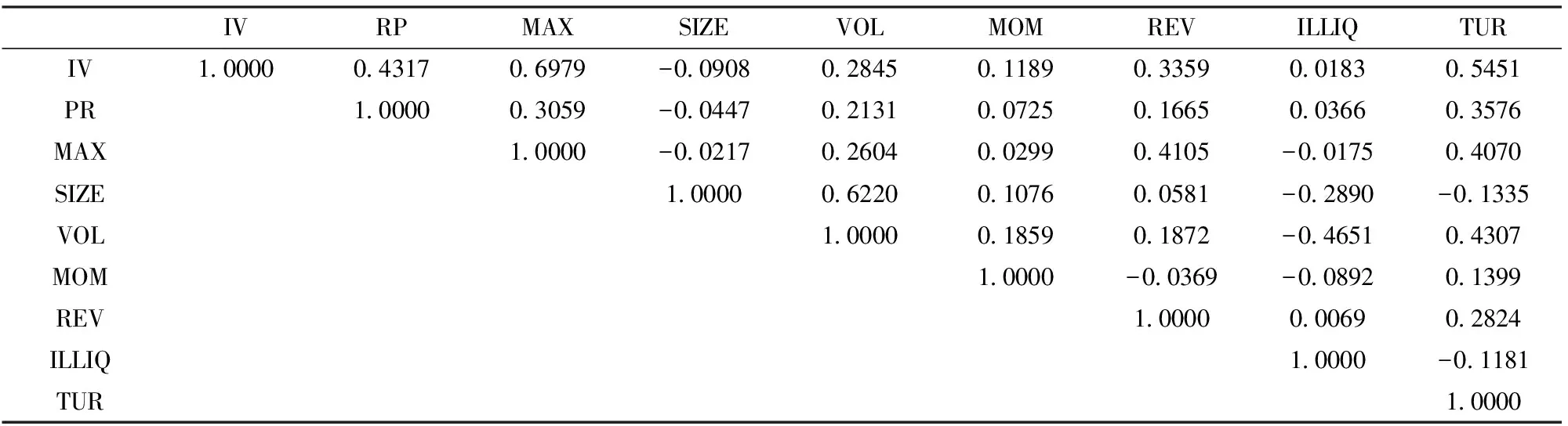
表4 横截面回归自变量相关系数的时间序列平均值

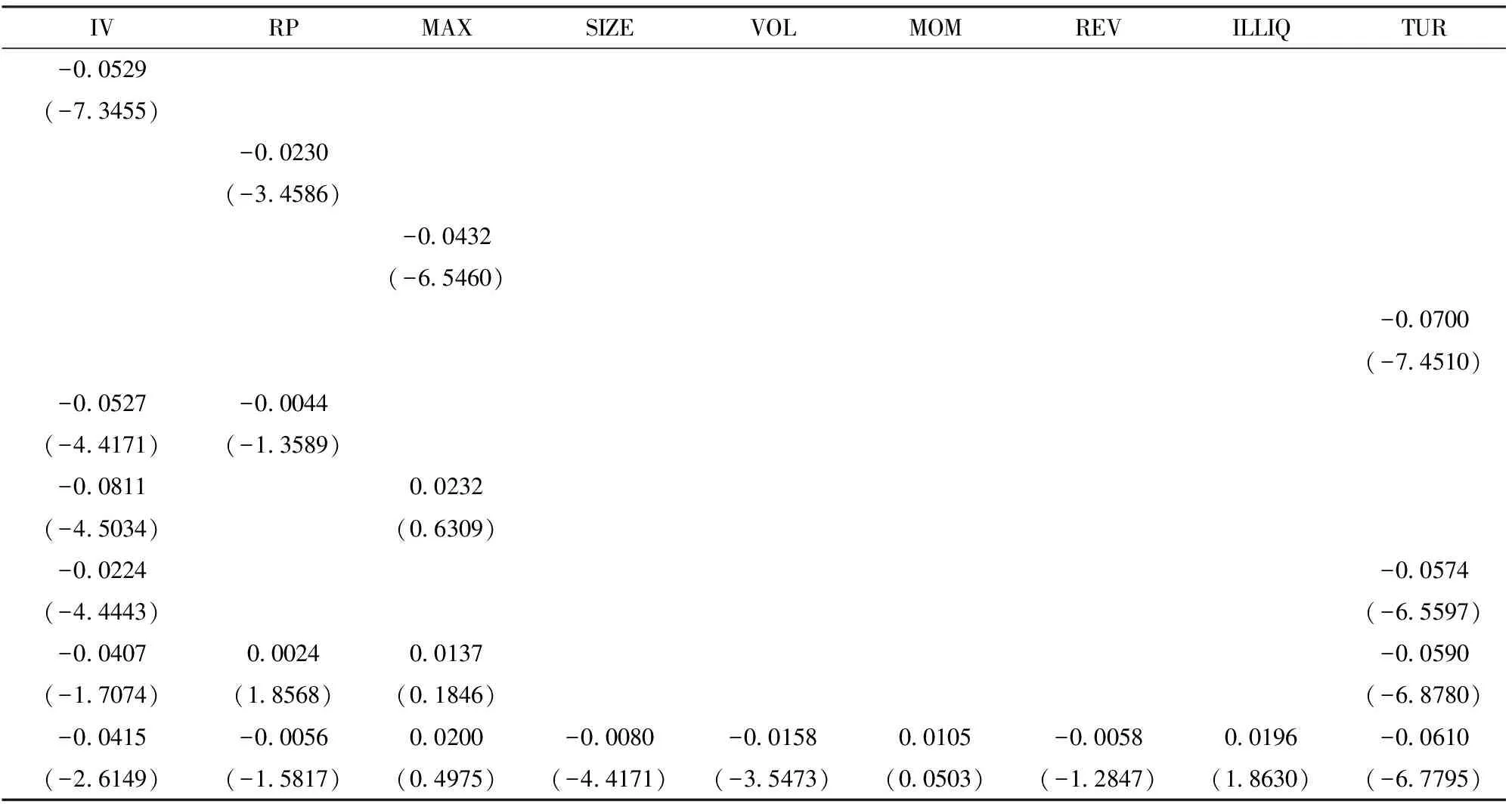
表5 横截面回归的结果

4 结语

特质波动率与股票预期收益之间的负向关系有悖于“高风险有高回报”的金融风险定价逻辑，对经典资本资产定价理论和市场有效性理论提出了极大挑战。“特质波动率之谜”产生的原因何在？个人投资者投机心理较强，喜欢过去价格变化幅度较大的股票，试图在股票低价时买进，高价时卖出，在价格上涨时买进，在价格暴涨时卖出，这种投资偏好现象令我们产生了浓厚的兴趣。与整个股票市场相比，价格变化幅度较大的股票，特质波动率往往也较大，投资者对这类股票的大量投资和频繁交易将会使其未来收益偏低。

我们以中国股票市场A股为研究对象，首先验证了中国股票市场确实存在“特质波动率之谜”，并且引入规模、动量、交易量、流动性、换手率、短期反转、最大日收益率等控制变量后，“特质波动率之谜”依然稳健存在。投资组合分析表明，以价格极差作为刻画股票价格变化幅度的度量指标，发现价格极差与换手率和最大日收益率相类似，可以在一定程度上解释但不能完全解释“特质波动率之谜”。投资者偏好价格变化幅度较大的股票可能是产生“特质波动率之谜”的部分原因。Fama-MacBeth横截面回归分析表明，以价格极差、最大日收益率、换手率同时作为控制变量，特质波动率与股票预期收益之间的负向关系不再显著。因此，结合现有文献的研究结果，投资者在投机心理的推动下，对历史价格变化幅度较大股票的偏好，喜欢像彩票类股票的博彩心理，以及反映投资者的异质信念共同构成了产生“特质波动率之谜”的主要原因。

解释“特质波动率之谜”不仅支持了“高风险有高收益”的资本资产定价逻辑，也为基于不完全信息的资本市场均衡模型提供了证据。同时，规范和完善上市公司信息披露制度，加强信息披露质量，提高信息披露速度，增强投资者的风险防范意识，减少短线投机行为，也是消除“特质波动率之谜”的一个可行方向。

参考文献：

[1] French K, Poterba J.Investor diversification and international equity markets[J].American Economic Review, 1991, 81(2): 222-226.

[2] Daniel K, Titman S.Evidence on the characteristics of cross sectional variation in stock returns[J].Journal of Finance, 1997, 55: 1-33.

[3] Cohen L.Loyalty-based portfolio choice[J].Review of Financial Studies, 2009, 22(3): 1213-1245.

[4] Hong H, Kacperczyk M.The price of sin: The effects of social norms on markets[J].Journal of Financial Economics, 2009, 93(1): 15-36.

[5] Hong H, Kostovetsky L.Red and blue investing: Values and finance[J].Journal of Financial Economics, 2012, 103: 1-19.

[6] Kumar A.Who gambles in the stock market?[J].Journal of Finance,2009, 64(4): 1889-1933.

[7] Bali T G, Cakici N, Whitelaw R F.Maxing out: Stocks as lotteries and the cross-section of expected returns[J].Journal of Financial Economics, 2011, 99: 427-446.

[8] Levy H.Equilibrium in animperfect market: A constraint on the number of securities in the portfolio[J].American Economic Review, 1978, 68: 643-658.

[9] Merton R.A simple model of capital market equilibrium with incomplete information[J].Journal of Finance, 1987, 42(3): 483-510.

[10] Campbell J, Lettau M, Malkiel B, et al.Have individual stocks become more volatile? An empirical exploration of idiosyncratic risk[J].Journal of Finance, 2001, 56(1): 1-43.

[11] Goetzmann W, Kumar A.Why do individual investors hold under-diversified portfolios?[R].Yale University working paper, 2004.

[12] Ang A, Hodrick R J, Xing Yuhuang, et al.The cross-section of volatility and expected returns[J].Journal of Finance, 2006, 61(1): 259-299.

[13] Fama E F, French K R.Common risk factors in the returns on stocks and bonds[J].Journal of Financial Economics, 1993, 33: 3-56.

[14] Bali T G, Cakici N.Idiosyncratic volatility and the cross section of expected returns[J].Journal of Financial and Quantitatie Analysis, 2008, 43(1): 29-58.

[15] Jiang G J, Xu D, Yao Tong.The information content of idiosyncratic volatility[J].Journal of Financial and Quantitatie Analysis, 2009, 44(1): 1-28.

[16] Han B, Kumar A.Retail clienteles and the idiosyncratic volatility puzzle[R].University of Texas at Austin working paper, 2008.

[17] 杨华蔚, 韩立岩.中国股票市场特质波动率与横截面收益研究[J].北京航空航天大学学报(社会科学版), 2009, 22(1): 6-10.

[18] 左浩苗, 郑鸣, 张翼.股票特质波动率与横截面收益: 对中国股市“特质波动率之谜”的解释[J].世界经济, 2011, 5: 117-135.

[19] Huang Wei, Liu Qianqiu, Rhee S G, et al.Return reversals, idiosyncratic risk, and expected returns[J].Review of Financial Studies, 2010, 23(1): 147-168.

[20] Chabi-Yo F.Explaining the idiosyncratic volatility puzzle using stochastic discount factors[J].Journal of Banking and Finance, 2011, 35(8): 1971-1983.

[21] 黄波, 李湛, 顾孟迪.基于风险偏好资产定价模型的公司特质风险研究[J].管理世界, 2006, 11: 119-127.

[22] 徐小君.公司特质风险与股票收益——中国股市投机行为研究[J].经济管理, 2010, 32(12): 127-136.

[23] 邓雪春, 郑振龙.中国股市存在特质波动率之谜吗?[J].商业经济与管理, 2011, 1: 60-67.

[24] Malkiel B G, Xu Yexiao.Idiosyncratic risk and security returns[R].Working paper University of Texas at Dallas, 2002.

[25] Asparouhova E N, Bessembinder H, Kalcheva I.Liquidity biases in asset pricing tests[J].Journal of Financial Economics, 2010, 96(2): 215-237.

[26] 梁丽珍, 孔东民.中国股市的流动性指标定价研究[J].管理科学, 2008, 21(3): 85-93.

[27] Pastor L, Stambaugh R F.Liquidity risk and expected stock returns[J].Journal of Political Economy, 2003, 111(3): 642-685.

[28] Amihud Y.Illiquidity and stock returns: Cross-section and time-series effects[J].Journal of Financial Markets, 2002, 5(1): 31-56.

[29] Jegadeesh N, Titman S.Returns to buying winners and selling losers: implications for stock market efficiency[J].Journal of Finance, 1993, 48(1): 65-91.

[30] Jegadeesh N.Evidence of predictable behavior of security returns[J].Journal of Finance, 1990, 45(3): 881-898.

[31] Boehme R D, Danielsen B R, Sorescu S M.Short-sale costs, differences of opinion and overvaluation[J].Journal of Financial and Quantitative Analysis, 2006, 41(2): 455- 487.

[32] Newey W K, West K D.A simple, positive semi-definite, heteroskedasticity and autocorrelation consistent covariance matrix[J].Econometrica, 1987, 55: 703-708.

[33] Spiegel M, Wang Xiaotong.Cross-sectional variation in stock returns: Liquidity and idiosyncratic risk[R].Yale University working paper, 2006.

[34] Fama E F, Macbeth J D.Risk, return, and equilibrium: Empirical tests[J].Journal of Political Economy, 1973, 81(3): 607-636.