综合面试中的均衡分组方法

陈 媛，樊治平，谢美萍

(1.上海财经大学信息管理与工程学院，上海 200433；2.东北大学工商管理学院，沈阳 辽宁 110819)

1 引言

综合面试是面试官通过面对面的交谈与观察的方式对面试者的素质进行主观评价，并结合其笔试成绩(客观评价)来综合判定面试者是否具备必备的素质[1]。近年来，综合面试被广泛应用在企事业单位招聘、公务员考录、领导者公开选拔、大学(研究生)入学考试等各种类型的招录过程中。由于综合面试结果直接关系到面试者的发展机遇和利益，公平、公正和客观被公认为是对综合面试的根本要求[2]。由于多数情况下面试者数量较多，为保证面试高效进行，招录单位的管理人员通常将面试者分为多个面试小组同时开展面试工作。一直以来，综合面试的分组由管理人员主观决策、手工操作，不仅具有一定的随意性，还影响了公平、公正和客观目标的达成以及面试效率的提高。因此，需要制定一项可行的策略来协调综合面试中的分组决策。

近年来，有关综合面试的研究一直是学界的关注重点，主要的研究主题包括面试效度[1]、面试制度与程序[3]、面试方法[4-6]以及面试成绩评价[7-8]等，这些研究成果从不同角度丰富了学界对综合面试的认识，对推动综合面试制度的完善起到了重要作用，但综合面试中的分组问题尚未引起足够重视，较少见到相关研究成果。需要指出的是，在许多领域内都存在分组问题，比较典型的有应急救援人员分组问题[9]、作业小组分组问题[10]、项目分组问题[11-12]、专家分组问题[13-14]、学生分组问题[15-17]、竞赛队伍分组问题[18]及数据分组问题[19]等。上述研究成果中，关于分组问题的分组思路及分组方法等均有明显不同，例如，樊治平等[9]依据救援人员的表现对救援人员分组，使分组后完成救援任务的效果最好，并提出了基于优化模型的分组方法；Chen Yuan等[13]从差异化的视角，采用了非线性优化模型对评审专家分组，使分组后各专家的背景尽量不同；朱帮助等[19]利用数据挖掘的方法，对电子商务交易数据进行分组处理，预测电子商务中的客户流失。可见，在当前分组问题研究方面存在的客观事实是分组问题背景的差异决定了很难有统一的分组思路和方法。

可以认为，综合面试分组的结果为面试官构造了一种决策的情境，为面试者创造了一个竞争的环境。为减小面试官主观判断过程中的情境依赖和参照效应[20-21]的影响，构建公平的竞争环境，本文提出均衡分组的思想：综合考虑面试者的特征信息，在分组时尽量使特征信息在各组之间均衡分布，使各小组具有相似(相同)的结构。均衡分组体现了这样的管理思路：通过控制面试者特征信息在各组中的分布，实现各小组在面试者组成结构方面相同或相似，使面试官的决策情境与面试者的受试环境与不分组情形尽可能一致。与现有的分组方式相比，均衡分组不仅会提高分组效率，而且避免了分组差异引起的面试结果偏差，对综合面试分组问题是一个很好的解决思路。

有鉴于此，本文采用均衡分组思想来解决综合面试的分组问题，并提出综合面试中的均衡分组方法，该方法首先建立了一个双目标优化模型，并设计了求解模型的遗传算法。

2 问题的提出

在综合面试中，面试官对面试者的主观判断具有情境依赖[20-21]。决定面试官判断的不仅是面试者的表现，还有许多情境因素。在不同情境下，同一位面试官对同一面试者的判断可能会完全不同，举例说明如下。假设有6位面试者，采用自然数编号，根据他们笔试成绩的排序为1>2>3>4>5>6，对同一位面试官，考虑两种情境，如图1所示。

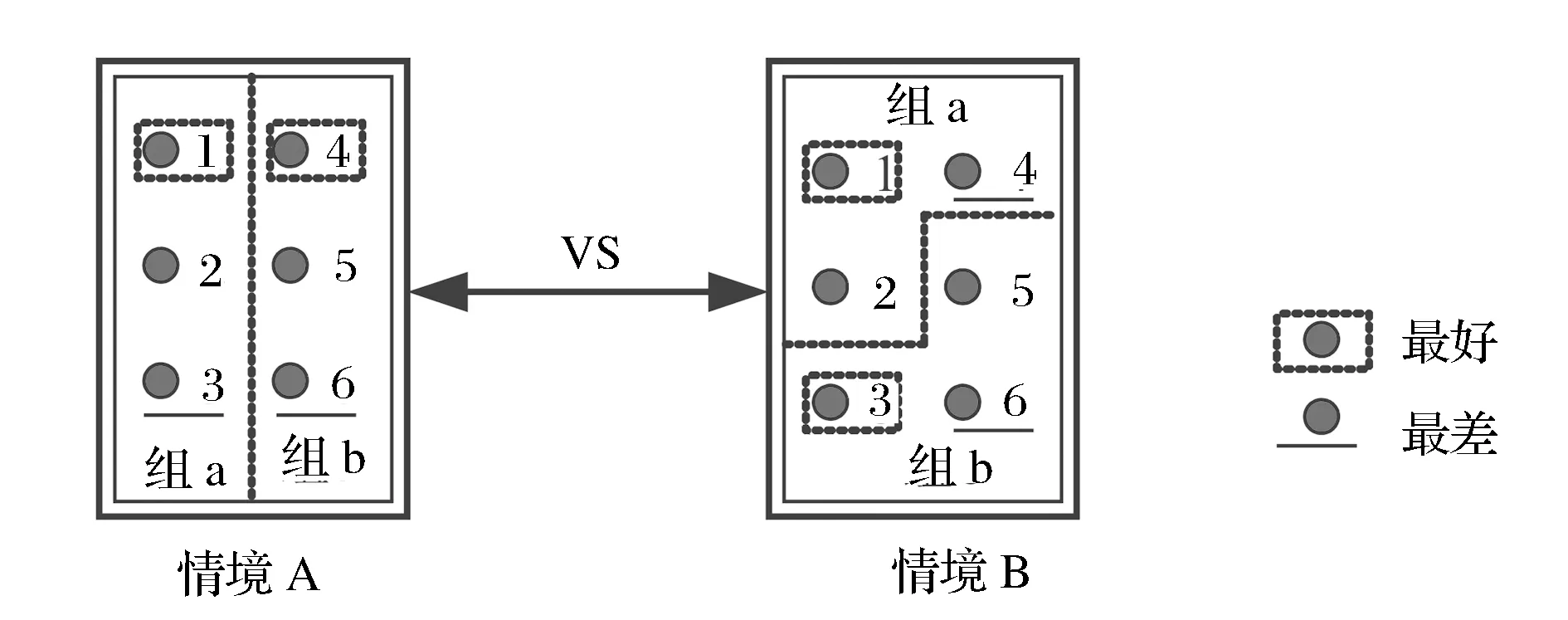
图1 两种判断情境比较

根据图1，在情境A中，面试官会认为：组a中1成绩最好，3成绩最差，组b中4成绩最好，6成绩最差；在情境B中，面试官会认为：组a中1成绩最好，4成绩最差，组b中3成绩最好，6成绩最差。比较两种情境，可以看出，3和4由于所在小组不同使面试官对其成绩的理解差异很大。通常情况下，不仅是面试者的笔试成绩，面试者的性别、年龄、职业等多种特征信息的综合形成了对面试官的刺激，使其面试时的主观判断具有明显的参照效应，影响其判断的准确性[20-21]。

另一方面，分组过程本质上是创造一个面试者水平对比的环境，对面试者来说，参照效应具体体现为：分到实力水平对比不同的小组，其通过(或被淘汰)的可能性的差异。这种情况常见于体育比赛的分组赛中，参赛者(队)期望分到实力较弱的小组，这样出线机率更大。在上例中，显然，3希望处于情境A中，4则希望处于情境B中。综合性面试分组中，有时为管理方便，每个面试小组要满足一定的淘汰率，这种管理手段更增大了分组的偶然性对面试结果的影响。

根据均衡分组的思想，在上例中，令组a由1、3、5构成；组b由2、4、6构成，各组内面试者笔试成绩的排序分别为：组a：1>3>5；组b：2>4>6。在这种情境下，面试官会认为：组a中1成绩最好，5成绩最差；组b中2成绩最好，6成绩最差。可见，无论面试官评审哪个小组，他对成绩的理解与六位面试者笔试成绩排序是一致的。对于任何一位面试者来说，他在组a或组b组中所处的竞争地位也与笔试成绩排序相符。因此，既然分组是客观事实，由于均衡分组后每个小组面试者笔试成绩排序的特征没有违背分组前的特征，这种分组结果对于面试官和面试者来说都较合理。需要指出的是，上例中仅涉及笔试成绩一项特征信息，在实际问题中常需要考虑多种特征信息，许多特征信息还需要进行相应的转换，因此，合理的分类与度量特征信息十分重要，此外，还要根据实际问题的要求设定特征信息的权重。

综上，采用均衡分组的思想，使各面试小组在面试者特征信息方面具有相同或相似的结构，不仅可以使面试官处于相似的情境以减小参照效应的影响，还可以为面试者创造相似的竞争环境。

3 模型的构建

记S={s1,s2…,sm}表示面试者的集合，共有m位面试者，G={G1,G2…,Gn}表示面试小组的集合，共有n个面试小组；记q表示每组中的面试者数量，通常有q=m/n。通过上述分析，构建综合面试中的均衡分组模型，具体过程如下：

定义1[22]：对于集合∀Ii⊆I，集合族π={Ii|Ii⊆I}为集合I的一个划分当且仅当Ii同时满足以下三个条件：

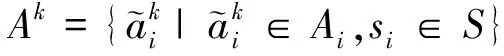
(2) 构建目标函数。设模型的决策变量为xij，且有

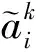
图2 均衡分组示意图

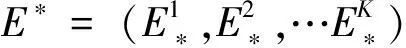
(1)

(2)

minZ2=minmax{dj}

(3)

(3)建立数学模型。综上，综合面试中均衡分组模型为

(2a)

minZ2=minmax{dj} (j=1,2,…,n)

(3a)

(4)

(5)

xij取0或者1

(6)

4 算法

这是一个双目标优化问题，常用多目标的处理方法是加权和方法[23]。记w1，w2分别为两个目标的权重系数，取两个目标的加权和为新的目标函数，即：

(7)

用式(7)代替式(2a)和(3a)，将原问题转化为单目标的0-1规划模型。

此外，考虑到(3a)是广义目标函数，用传统软件包难以求解，而且面试者数量较多时，问题的规模较大，因此本文采用遗传算法求解。在经典遗传算法中，染色体编码常采用顺序编码，这种编码方式对于分组问题来说，存在大量编码冗余。考虑到综合面试均衡分组问题中既有面试者又有面试小组，在文献[24]和[25]的基础上，本文设计了染色体的两段式编码，用个体段和组段分别表示相应的个体信息和组信息，具体如下：

r1,r2,…rm|U1,U2…,Un

(8)

式(8)中，ri∈{1,2,…,n} 表示si被分到了小组ri中(i∈{1,2,…,m}),Uj∈{1,2,…,n}为第j个小组的自然数编号。在此基础上，给出了求解模型的遗传算法，算法步骤如下：

步骤1：产生初始种群。采用两段式编码，构造可行分组的染色体，即依次将si指派到组Gj中，形成集合S的划分，在此基础上形成初始种群。

步骤2：选择交叉操作的染色体。将(7)作为适值函数，采用轮盘赌策略，确定进行步骤3的父代染色体。

步骤3：进行交叉操作。对步骤2中选择的父代染色体进行交叉操作，修复不合法的子代染色体，具体分为：

步骤3.1: 将父代染色体之间的组段信息进行注入(Inject)，产生子代染色体的组段信息;

步骤3.2: 根据子代染色体的组段信息确定个体段信息;

步骤3.3: 对不合法的子代染色体进行修复，修复过程如下：

R1:IFri对应的si重复出现，

THEN删除多余的si，使其只出现一次；

R2:IFUj对应的Gj出现多次或组数大于n，

THEN合并多余的小组，使组数恰好等于n；

R3:IF|Gj|≠q,

THEN协调组间内的个体，使每组个体数恰等于q。

现举例说明交叉操作过程。假设需要将9位面试者分为3组，每组3人，经过步骤2选择的父代染色体分别为父代1和父代2，他们进行的交叉操作过程如图3所示。首先将父代2的部分组段信息注入父代1的组段信息，得到子代染色体的组段信息，根据(8)的编码方式，确定子代染色体的个体段信息，可以观察到，所产生的子代染色体中某些个体在多个组中重复出现，而且小组数量也不满足要求，显然，该子代染色体是不合法的，需要对其修复。在修复时首先删除出现多次的个体(图中用斜线标示),进一步，合并多余小组使小组数量恰等于3。注意到合并后G2和G3内的面试者数量不符合要求，因此将s7从G3中调整到G2。最后，得到合法的子代染色体。

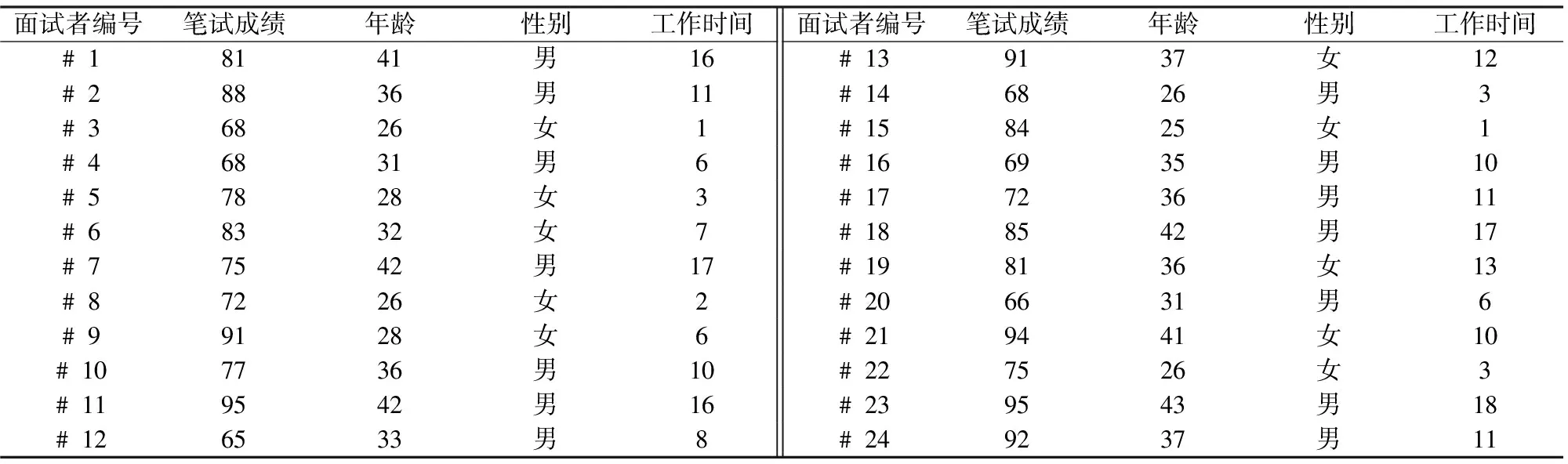
步骤4：进行免疫操作。随机选择两个染色体，产生随机数ε(ε

步骤5：重复上述步骤，直到指定最大代数，停止运算。

以上遗传算法用JAVA编程，通过大量随机数据实验计算，取得了很好的效果。特别地，该算法可以用于解决满足约束(4)和(5)的一类分组问题。

5 算例

某高校商学院MBA招生考试中，根据笔试成绩确定24名考生参加面试。为了使面试高效进行，管理人员拟将面试考生分为4个小组同时展开面试。结合MBA招生的要求，在分组时需要综合考虑考生的笔试成绩、年龄、性别和工龄等特征信息，考生的基础信息如表1所示，现需确定该校商学院MBA面试的均衡分组方案。

表1 MBA面试者的基础数据

表2 MBA面试者的特征信息值向量

最后，构建分组模型并求解，得到该校商学院MBA面试分组方案如表3所示，这里，令w1=w2=1，λk=1，k=1,2,3,4。

表3 分组结果

根据表3的分组结果，分别考察每种特征信息在各组中的分布情况，如图(4)-(7)所示。

图4 笔试成绩

图5 年龄

图6 工龄

图7 性别

从图(4)-(7)中可以看出，在考察的特征信息中，对于笔试成绩、年龄以及工龄三个特征信息，每个小组均含有各段的面试者至少一位、至多两位；对于性别，每个小组至少包含一种性别三位、至多四位。根据上述数据，进一步比较均衡分组情形与不分组情形下特征信息在不同分段内面试者数量比，如表4所示。

表4 均衡分组与不分组的比较

根据表4，均衡分组后特征信息在各组内分布均衡，四个小组的结构相似，并且与不分组情形大致相当，即面试官和面试者所处的小组环境与不分组情形基本一致。需要指出的是，算例中各特征信息的权重系数λk是相同的，由于特征信息之间有时会相互冲突，因此，应根据综合面试实践的需求，通过调整λk来确定分组所需考虑特征信息的优先级。

6 结语

综合面试中的分组是实践中提高工作效率的一种管理手段，缺乏科学合理依据的分组不仅会影响到面试官的判断，还关系到面试者能否具有公平的受试环境。本文提出了一种使分组决策更加科学、合理的分组方法。这种方法采用均衡分组的思想，构建了分组的双目标优化模型，并结合模型的特点，提出了遗传算法。通过均衡分组，各面试小组的结构相似并尽可能符合不分组情形，减少了由于分组可能产生负面效应，不仅能够降低综合面试中管理者的手工操作负担，提高工作效率，更有助于综合面试的公平、公正、客观目标的达成。

参考文献：

[1] 洪自强, 严进.结构化面试构思效度现场研究[J].南开管理评论, 2003, 6(4):21-24,68.

[2] Arvey R, Campion J.The employment interviewer: A summary and review of recent research[J].Personnel Psychology, 1982, 35(2): 281-322.

[3] 孙嫦婵, 江莹.试论研究生复试中的程序公正[J].扬州大学学报(高教研究版),2005,9(2): 60-63.

[4] 江莹.评价中心对研究生复试的启迪[J].河北大学学报(哲学社会科学版), 2005, 30(2): 65-68.

[5] 刘节, 萧鸣政.企业面试中存在的常见问题及对策浅析[J].人才资源开发, 2006,(12):25-27.

[6] 萧鸣政.人才测评与选拔[M].上海：复旦大学出版社, 2005.

[7] 白榕.AHP法在研究生复试质量保障体系中的应用[J].重庆交通学院学报, 2005,24(4): 157-159.

[8] Hua Zhongsheng, Jiang Wenqi, Liang Liang.Adjusting inconsistency through learning in group decision-making, and its application to China's MBA recruiting interview[J].Socio-Economic Planning Sciences, 2007,41(3): 195-207.

[9] 樊治平,刘洋，袁媛，等.突发事件应急救援人员的分组方法研究[J].运筹与管理, 2012, 21(2): 1-7.

[10] 樊治平，徐宝福，刘洋，等.一种面向细胞生产的作业小组组建方法[J].工业工程与管理, 2010, 15(3): 41-44.

[11] CookW D, Golany B, Kress M, et al.Optimal allocation of proposals to reviewers to facilitate effective ranking[J].Management Science, 2005, 51(4): 655-661.

[12] Hochbaum D S, Levin A.Methodologies and algorithms for group-ranking decision [J].Management Science, 2006, 52(9): 1394-1408.

[13] Chen Yuan, Fan Zhiping,Ma Jian, et al.A hybrid genetic algorithm for reviewer group construction problem[J].Expert Systems with Applications, 2011, 38(3): 2401-2411.

[14] 汪定伟, 刘铸.社会考试评卷人分组的多目标优化模型[J].控制与决策, 2004, 19(9): 1026-1029.

[15] Mingers J, O’brien F A.Creating students groups wth similar characteristics: A heuristic approach[J].Omega, 1995, 23(3): 313-321.

[16] Weitz R R, Jelassi M T.Assigning students to groups: A multi-criteria decision support system approach[J].Decision Sciences, 1992, 23: 746-757.

[17] Saber H M, Ghosh J B.Assigning students to academic majors[J].Omega, 2001, 29(6): 513-523.

[18] 程嘉炎.球类运动竞赛法[M].北京: 人民体育出版社, 2003.

[19] 朱帮助,张秋菊，邹冥飞，等.基于OSA算法和GMDH网络集成的电子商务客户流失预测[J].中国管理科学, 2011, 19(5): 64-70.

[20] Kahneman D, Slovic P, Tversky A.Judgment under uncertainty: Heuristics and biases[M].Cambridge:Cambridge University Press, 1982.

[21] Plous S.The Psychology of Judgment and Decision Making[M].New York:McGraw-Hill, 1993.

[22] 谢美萍.离散数学[M].北京：清华大学出版社, 2008.

[23] Steuer R E.Multiplecriteria optimization: theory, computation, and application[M].NewYork: Wiley, 1986.

[24] Falkenauer E.Genetic algorithms for grouping problems[M].Wiley: New York, 1998.

[25] Fan Zhiping, Chen Yuan,Ma Jian,et al.A hybrid genetic algorithm for maximally diverse grouping problem[J].Journal of Operational Research Society, 2011, 62(1): 92-99.