不同面积Kapton材料的放电特性实验研究
2014-04-09刘海波李得天杨生胜汤道坦王婷婷
刘海波,李得天,杨生胜,汤道坦,柳 青,王婷婷
(兰州空间技术物理研究所 真空低温技术与物理重点实验室,甘肃 兰州 730000)
0 引言
暴露在空间等离子环境中的航天器表面材料在入射的电子、离子、表面光电发射、背散射电子及漏电流作用下积累电荷,可使材料充至数十千伏的电位[1]。当充电电位达到放电阈值时,就会产生放电现象。放电诱发的对“地”瞬态脉冲会干扰航天器上电子仪器的正常工作,严重时使航天器发生故障,无法完成在轨运行任务。
在空间等离子环境下,不同面积航天器表面绝缘材料的充电电位、电荷贮存量和能量差异较大,可能引起其放电电流峰值、放电电荷损失量和放电能量损失有所不同。通过对不同面积的Kapton材料进行放电实验,探索其放电特性规律,可以根据这些放电特性规律制定材料的应用方案、设计滤波器、选择元器件和优化电路等方式减小其放电对航天器正常工作的影响。
加拿大的Balmain、Kremer等和路易斯研究中心的Paul等分别对小于100 cm2和232~5 085 cm2的航天器表面绝缘材料进行了放电实验研究,其得出的研究结果存在较大差异。研究表明材料面积小于100 cm2时,放电电流峰值同面积呈线性关系;而当材料面积在232~5 085 cm2时,放电电流峰值同材料面积的关系为Im-s0.4[2-5]。针对Kapton材料开展了地面模拟放电实验研究,文章得出各放电特性和放电波形同材料面积的关系,并综合本次实验数据和国外研究结果,提出能够适应以上差异的结论。
1 实验装置及方法
针对航天器表面常用的Kapton温控材料,分别制作了20 mm×20 mm、40 mm×40 mm、50 mm×50 mm、60 mm×60 mm、80 mm×80 mm、100 mm×100 mm、140 mm×40 mm、150 mm×150 mm的正方形铝板,在铝板上用导电银胶黏贴125μm厚的Kapton材料作为实验样品。样品实物图如图1所示。

图1 样品实物图
实验中将真空系统抽至6×10-4Pa的真空度来模拟空间真空环境。使用德国STAIB电子枪模拟空间电子辐照环境。由于地球同步轨道航天器进入地磁亚暴引起的增强等离子区域时容易发生充放电现象,这里根据地磁亚暴期间的环境参数,选用能量为25 keV,束流密度为2.5 nA/cm2的电子对样品进行辐照。实验中采用取样电阻的方式来测量放电波形,测量电路如图2所示。
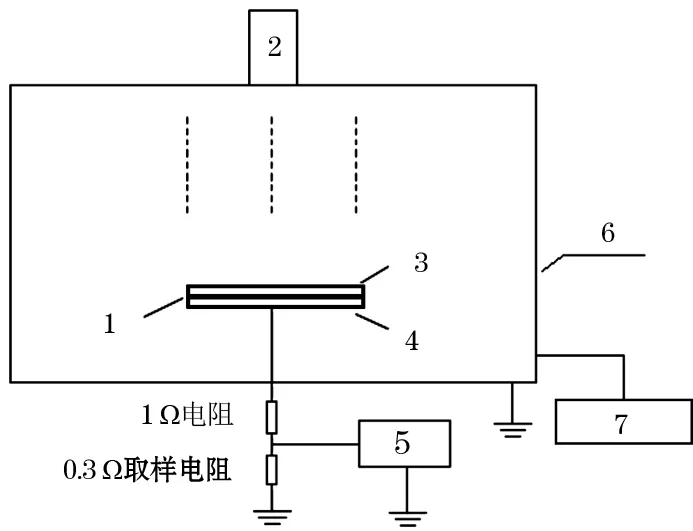
图2 地面模拟放电实验系统示意图1.导电银胶;2.电子枪;3.kapton材料;4.铝板;5.示波器;6.真空室;7.抽真空系统
通过前期摸底实验发现,采用在放电回路中串联1 Ω和0.3 Ω的电阻,将0.3 Ω电阻作为取样电阻来测量放电脉冲波形的方式能够很好的测量放电信号。
根据以上设计的样品和测量方法,构建如图2所示的实验系统。由于电子束对同轴电缆的绝缘外表皮充电可能引起放电干扰,影响对样品放电波形的测量。因此对同轴电缆进行了外层屏蔽,即给同轴电缆外部包覆了一层0.3 mm的铜箔,并对其进行接地处理,避免在铜箔上产生悬浮电位。
2 实验结果及分析
2.1 放电脉冲波形分析
由实验中的波形数据得出20 mm×20 mm、40 mm×40 mm、50 mm×50 mm、60 mm×60 mm的正方形Kapton样品的典型放电波形如图3所示。

图3 不同面积Kapton材料典型放电波形
由实验中的波形数据得出80 mm×80 mm、100 mm×100 mm、140 mm×140 mm 、150 mm×150 mm正方形Kapton样品有如图4(a)、(b)、(c)所示的三种典型放电波形。

图4 不同面积Kapton材料典型放电波形
将图3波形和图4(a)、(b)、(c)波形对比,可知小面积Kapton材料的放电脉冲更窄,且有一个明显的负向峰值。由图4(b)看出大面积材料放电诱发的瞬态脉冲波形会出现两个波峰,而且由更多的实验数据对比发现,材料的面积越大,会呈现出更明显的双峰波形,在150 mm×150 mm的Kapton样品中甚至出现三个波峰的波形。结果表明面积大的材料,初次放电只能将材料表面部分区域的电荷泄放出去,初次放电后造成的局部电荷损失在放电点附近产生了超过放电阈值的电势差,从而诱发了第二次放电,两次放电的波形叠加在一起就形成了图4(b)所示的双峰波形。面积越大的材料,上述效应就更明显,所以更容易出现双峰,甚至三个波峰的波形。由图4(c)可看出,在波形到达波峰后开始缓慢下降,这可能是由于在金属板和地之间加了电阻,在放电结束后电阻引起的阻尼振荡的结果。而且图4(c)所示的放电波形的放出电荷量和能量都很大,由图4(c)中的细线所示数值计算得出其放出电荷量为233.3μm,如果该波形出现在在轨运行的航天器中,则可能引起严重的电子线路故障。
2.2 放电特性与Kapton材料面积关系分析
实验中得出的放电电流峰值、放电持续时间、放电电荷损失量、放电频率同材料面积关系的数据如表1所列。
通过对表1所列实验数据总结,得出放电电流峰值、放电持续时间、放电电荷损失量、放电频率f和材料面积关系曲线分别如图5、6、7、8所示。

表1 125厚Kapton材料地面模拟放电实验数据

图5 Kapton材料面积同放电电流峰值的关系曲线

图6 Kapton材料面积同放电持续时间的关系曲线

图7 Kapton材料面积同放电电荷损失量的关系曲线

图8 Kapton材料面积同放电频率的关系曲线
由图5可知,随着Kapton材料的面积增大,其放电电流峰值也随之升高。而且其斜率随着面积的增大而降低。图5中的曲线为拟合曲线,拟合关系如下面式(1)所示。
(1)
式中:Im为放电脉冲电流峰值,A;S为Kapton材料面积,cm2。
在Balmain的研究中,虽然根据实验数据得出聚酯薄膜材料的面积同放电电流峰值之间的线性拟合关系,但是从文章中的数据曲线可知,其小面积材料放电电流峰值数据点和材料面积明显不呈线性关系,而是如图5所示曲线相似的非线性关系[4]。而且在Kapton材料的研究中,小面积Kapton材料的面积同电流峰值关系数据点的离散状况比较严重[3]。可见对于小面积的航天器表面绝缘材料,其放电电流峰值同材料面积并不呈线性关系,图5所示的曲线能够真实的反映小面积材料的面积同放电电流峰值的关系。
结合Paul R. Aron和John V. Scaskus对大于232 cm2的Teflon材料的研究,电流峰值同材料面积呈Im~s0.4关系[5],关系曲线随着面积的增大斜率应不断的减小,而从式(1)可看出,曲线斜率也随着材料面积的增大而减小。综合以上考虑,式(1)中提出的关系能够实际的反映材料放电电流峰值同材料面积的关系。Paul R.Aron和John V.Scaskus之所以提出大多数放电电流峰值和面积几乎没有关系[5],是由于大面积材料对应的曲线斜率很小,在实验误差作用下,观察不到相应的面积同放电电流峰值的比例关系。
由图6(a)、(b)可知,随着材料面积增大,对应的放电持续时间越长。根据加拿大在提出的放电传播理论[3],这可能是由于面积大的材料,放电时可形成的放电隧道更长,在放电传播速度一定的情况下,材料内部的电荷需要经过更长路径的电荷迁移才能到达放电点,所以放电持续时间也更长。由于大面积材料的放电诱发的瞬态脉冲波形中,存在如图4(c)所示的持续时间长的波形,在这里将小面积材料和大面积材料放电时间随材料面积的变化曲线分别进行处理。由图6(a)所示拟合曲线得出4 cm2、16 cm2、25 cm2、36 cm2Kapton材料同放电持续时间的关系式如下面式(2)所示。
Tm=198.684+2.411S
(2)
由图所示拟合曲线得出64 cm2、196 cm2、225 cm2Kapton材料同放电持续时间的关系式如下面式(3)所示。
Tm=1034.133+21.818×S
(3)
式(2)、(3)中,Tm为放电持续时间,ns;S为材料面积,cm2。

Qm=2.172+0.241S
(4)
由图7(b)所示拟合曲线得出64 cm2、100 cm2、196 cm2、225 cm2Kapton材料放电电荷损失量和材料面积的关系式如式(5)所示。
Qm=11.643+0.976S
(5)
式(4)、(5)中,Qm为放电电荷损失量,μC;S为材料面积,cm2。
Keith G. Balmain等得出的材料面积同放电电荷损失量的曲线斜率为1,从所做曲线的数据点可知,在曲线的小面积部分的数据偏差比较大[3],其曲线只能反映大面积Kapton材料放电电荷损失量同面积的关系。由(5)式可知大面积材料放电电荷损失量同材料面积的关系曲线的斜率为0.976,同Keith G. Balmain等的研究中得出的斜率基本一致。
由于表面材料的放电频率对航天器正常工作产生很大的影响,这里也对Kapton材料的放电频率同材料面积的关系进行研究。由实验数据得出材料面积同放电频率的关系曲线如图8所示。由图8可知,随着Kapton材料面积增大,放电频率也相应的升高,材料面积和放电频率之间呈线性关系。关于这方面的解释,面积越大的材料,能够满足放电条件的内部奇异点更多,造成其更容易发生放电。由图8所示拟合曲线得出放电频率同材料面积的关系如式(6)所示。
f=0.984+0.019S
(6)
式中:f为放电频率,次/h;S为Kapton材料面积,cm2。
对图5、6、7、8所示的曲线进行总结,得出随着材料面积增大,放电电流峰值、放电持续时间、放电时材料表面电荷损失量和放电频率都相应升高。基于航天器带电防护方面的考虑,在航天器上应用时应当尽量选取小面积的Kapton材料。
3 结论
通过对不同面积的航天器表面常用Kapton材料进行地面模拟放电实验,得出不同面积材料的放电脉冲波形规律和各放电特性同材料面积的关系,为材料在航天器表面上的应用、航天器表面带电防护和放电危害评估提供数据支持。在放电波形方面,通过对实验数据总结,得出低于36 cm2的Kapton材料,其放电脉冲波形的脉宽较窄,且出现明显的负向峰值,而当材料面积大于64 cm2时,出现双峰波形放出电荷量和能量都比较大的波形。在放电特性同材料面积的关系方面,实验数据表明随着材料面积的增加,其放电电流峰值、放电持续时间、放电电荷损失量和放电频率都相应增加。并根据实验数据画出各放电特性同材料面积的关系曲线,拟合出与其对应的关系式。在放电电流峰值和材料面积关系的研究中,针对国外在大面积材料(232~5085 cm2)和小面积材料(<100 cm2)研究中的矛盾,文章提出了一个解决方案,即Kapton材料的放电电流峰值和面积之间并不呈线性关系,而是随着材料面积增加,曲线斜率逐渐减小。在材料放电持续时间和电荷损失量同Kapton材料面积关系的研究中,得出和国外研究一致的线性关系,但是大面积材料和小面积材料呈现的线性关系有所不同。
参考文献:
[1]陈益峰,杨生胜,秦晓刚, 等.介质材料带电对二次电子发射影响的研究[J].真空与低温,2010,16(3):167-170.
[2]Balmain K G, Kremer P C, Cuchanski M. Charged-area effects on spacecraft dielectric arc discharges[J]. Reference, 1978, 3: 302-308.
[3]Balmain KG, Dubois GR. Surface Discharges on Teflon, Mylar and Kapton[J]. IEEE Transactions on Nuclear Science, 1979,26(6):5146-5151.
[4]BalmainKG.Scaling Law and Edge Effects for Polymer Surface Discharges[C]//Spacecraft Charging Technology, 1978:646-656.
[5]Paul R. Aron and John V. Staskus. Area Scaling Investigations of Charging Phenomena[C]//Spacecraft Charging Technology, 1978:485-506.
