铰接车铰接点位置分析与计算

贾小平， 樊石光， 于魁龙， 李 炯

(装甲兵工程学院机械工程系，北京 100072)

铰接式全地形车具有通过能力强、越障高、跨壕宽、爬坡度大、载重大等优点，还可以实现俯仰、扭转、横摆等单节车无法完成的动作[1]，断开后还能满足空运、空投的需求。图1铰接车通过使前后车体相对偏转一定的角度实现转向[2]，其动力传动路线如图2所示，主要通过液压泵和独立的4个马达将动力传递到前、后、左、右4个摆臂壳内[3]，再通过链传动将动力传递到8个驱动轮上。

图1 铰接车整车结构

图2 铰接车动力传动简图

1 转向阻力矩理论分析

对铰接车进行原地转向运动学及动力学分析，建立如图3所示坐标系[4]。

图3 铰接车原地转向力学模型

1.1 车轮转动阻力矩

当铰接车转向角变化时，轮胎产生以铅垂线为轴线的转动，且该轴线通过轮胎与地面接触面的形心。轮胎与地面接触面可视为a×b的矩形面积，当轮胎回转中心与该矩形面积的形心重合时，其转动阻力矩为

(1)

式中：G为轮胎负荷；μ为摩擦因数；a、b分别为接触面矩形面积的长、短边。当轮胎与地面接触面为椭圆形时，可将该椭圆转化为与其面积相等的等效矩形计算：

式中：x、y分别为椭圆接触面的长、短轴。由于本文低压胎与地面接触面是椭圆形，故其转向阻力矩[5]为

(2)

令整车8轮与地面的转向阻力矩分别为MA、MB、MC、MD、ME、MF、MG、MH，则前、后车体绕各自中心点转动的阻力矩分别为

(3)

(4)

式中：G1、G2分别为前、后半车载荷。

1.2 两侧车轮滚动方向不同产生的滚动阻力矩

铰接车原地转向时，内侧前、后车轮相互靠近，外侧前、后车轮相互远离，由此形成的前、后车架对应车轮的滚动阻力矩分别为

(5)

(6)

式中：f为滚动阻力系数；B为左、右侧车轮轮距。

算法综合比较了NLMS和FDNLMS算法的性能,比较指标包括处理时间以及自适应滤波器失调系数和回声返回损耗增益值:

1.3 静态转向阻力矩

静态转向阻力矩按虚位移原理计算，即

(7)

式中：Fi(i=1,2,…,n)为主动力;对应的ri(i=1,2,…,n)为第i个主动力所对应的虚位移[6]。

根据铰接车静态原地转向力学模型(图3)，令

k=L1/(L1+L2)=L1/L，

式中：L1、L2分别为铰接点距前、后半车中心点的距离；L=L1+L2。

当前后车体转动夹角为γ时，后半车与图3中虚线夹角为

β=arcsin(ksinγ)，

(8)

前半车与虚线夹角为

α=γ-arcsin(ksinγ)，

(9)

对式(8)、(9)进行变分，得到

(10)

(11)

则后半车中点P的虚位移为

(12)

将主动力和对应的虚位移代入式(7)，得到

解得静态原地转向阻力矩为

其中,F=φG1，φ=0.7，转向阻力矩计算参数和计算结果分别如表1、2所示。

表1 转向阻力矩计算参数

表2 转向阻力矩计算结果

2 铰接车虚拟样机建模

铰接车由前车体、后车体及铰接机构连接而成，整车通过铰接机构两侧对称布置的转向油缸实现折腰转向。整车实车重3.6 t，车长4 500 mm，车宽1 800 mm，轮胎外径为800 mm，摆臂臂长800 mm。转向阻力矩的大小与轮距、转向桥的桥荷、转向桥到铰接点的距离有关，调整任一个因素，都会影响转向阻力矩。假设：1)转向阻力矩与转向角速度无关；2)转向阻力矩在转向过程中为恒量。本文主要通过改变铰接点的位置来分析转向阻力矩的变化。

基于RecurDyn/Tire工具包，建立轮式铰接车仿真模型及整车原地转向路面，如图4所示。对机构中组成元件施加约束，通过Joint来建立约束副，以此来限制不同实体间的相对运动，使系统中各部件组成一个有机整体。对机构进行运动学/动力学分析，设置仿真时间t=3.4 s，步长step=800，对前后车体铰接点圆柱铰约束副施加0.5π的转速驱动[7]。对模型进行Dynamic/Kinematic分析并进行plot后处理，去除运行初始阶段的非稳态点，将运动稳定后的曲线数据点导出并保存。

图4 铰接车动力学仿真模型

3 仿真与结果分析

整车铰接点位置选取[8]如图5所示，l1=1 300 mm，l2=1 400 mm，在该坐标系中，分别选取铰接点坐标为s(1 350,0)、s1(1 950,0)、s2(2 700,0)，进行转向阻力矩仿真分析，得到不同铰接点位置下转向阻力矩曲线如图6所示。可以看出：在s和s1处，转向阻力矩曲线较为平稳；在s2铰接点(即后车体中心点处),测得的转向阻力矩数据波动性较大。为便于比较，将s2铰接点处的转向阻力矩曲线进行线性拟合处理。

图5 铰接点位置选取示意图

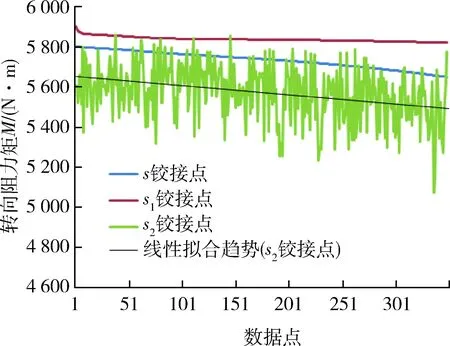
图6 不同铰接点位置下转向阻力矩曲线对比

对s铰接点处的转向阻力矩理论值和仿真值进行比较，结果如表3所示。

表3 s铰接点处转向阻力矩仿真值与理论值

由表3可知：在s铰接点处，静态转向阻力矩仿真值与理论值误差小于2.5%，在允许范围内。因此，仿真所得转向阻力矩可以作为铰接点位置优化选取的依据。

对s、s1、s2铰接点处的转向阻力矩仿真数据求取均值，结果如表4所示。

表4 原地转向阻力矩仿真值

结合图6可知：在铰接点坐标从s变化到s2的过程中，转向阻力矩出现先变大后变小的趋势，并且在s2铰接点处达到最小值。因此，将铰接点位置由s处更改到s2处,即从前、后车体中间前移到前车体几何中心上，如图7所示。

图7 铰接点改变前后铰接车模型对比

加宽轴距l2，令l2=1 550 mm，以s2作为研究点，则其坐标变为(2 850,0)，与s2(2 700,0)时进行对比，得到仿真转向阻力矩曲线如图8所示，仿真数据取均值，结果如表5所示。

表5 轴距改变前后s2铰接点处转向阻力矩仿真值

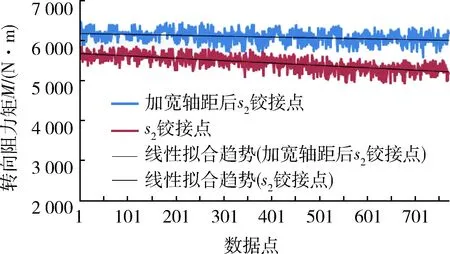
图8 轴距改变前后s2铰接点处转向阻力矩曲线对比

由表5可知：在铰接点s2处，当轴距l2加宽后，对应的转向阻力矩增大。

4 结论

以原地转向阻力矩最小为衡量目标，通过计算和动力学仿真，分析和选取铰接点的位置，为整车设计提供依据：在保证F、G和B、C轮转向过程中不发生干涉的情况下，轴距l2应尽可能缩短；将铰接点置于s2点，可使转向阻力矩最小。但铰接点位置的选取还受直驶稳定性、越障稳定性、整车布局、设计用途等因素的影响，文中并未考虑；这些因素之间可能存在矛盾，如铰接点在s2点时，铰接车直驶稳定性变差，易出现横摆现象。因此，下一步，还需对这些影响因素进行深入研究。

参考文献：

[1] Oida A．Turning Behavior of Articulated-frame-steering Tractors:Part 2.Motion of Tractors with Drawbar Pull[J]．Journal of Terramechanics，1987，24(1)：57-73．

[2] 王慧，侯友山，金纯．铰接车辆转向阻力矩的分析[J]．矿山机械，2010，38(1)：38-41．

[3] 闫清东，张连第，赵毓芹，等．坦克构造与设计[M]．北京：北京理工大学出版社，2007：211-232．

[4] 郭凌汾，黄海东，秦四成，等．铰接式车辆静态转向阻力矩分析[J]．农业机械学报，1995，26(1)：23-27．

[5] 汪建春．铰接式车辆原地转向阻力矩计算及力学模型计算[J]．矿山机械，2008，36(21)：53-58．

[6] 汪明德，赵毓芹，祝嘉光．坦克行驶原理[M].北京：国防工业出版社，1983：128-142．

[7] 焦晓娟，张湝渭，彭斌彬．RecurDyn 多体系统优化仿真技术[M]．北京：清华大学出版社，2010：325-362．

[8] 南基信，秦四成，阚君武，等．三桥铰接车辆动态转向阻力矩的分析和计算[J]．吉林工业大学学报，1996，26(1)：16-23．