广义并接图的无符号拉普拉斯谱半径
2014-04-08吴雅容
吴雅容
(上海海事大学 文理学院, 上海 201306)
1 相关定义与引理
1.1 定义
设图为G= (V,E),其中:V=V(G) = {v1,v2,…,vn} 为顶点集, |V| =n为图G的阶数;E=E(G) = {e1,e2,…,em}为边集, |E| =m为图G的边数. 若边e= (u,v) =uv的两个端点分别为顶点u和v, 则称顶点u与v相邻接, 记为u~v; 否则称它们不相邻, 记为uv. 若边e= (u,v)∈E, 则称顶点u或v与边e关联. 与顶点v关联的边的个数称为顶点v的度(或顶点v的次), 记作deg(v)=dv. 图G中最大、最小的顶点的度分别记为 △(G) 和δ(G). 用NG(v) 表示顶点v在图G中所有相邻的顶点所组成的集合. 若图G只有一个分支, 则称图G是连通的.
图G的邻接矩阵记为A(G) = (aij)n×n, 是一个n阶的(0,1)方阵, 其定义为
称矩阵Q(G) =D(G) +A(G) 为图G的无符号拉普拉斯矩阵. 这里,D(G)=diag (d1,d2,…,dn) 是以图G的相应顶点的度为元素的对角矩阵. 称det (qI-Q(G)) 为图G的无符号拉普拉斯特征多项式. 显然,Q(G)是一个实非负对称矩阵, 其n个特征值从大到小记为q1(G)≥q2(G)≥…≥qn(G)≥0, 其中:最大特征值q1(G) 称为图G的无符号拉普拉斯谱半径, 简记为q(G). 非负实矩阵Q(G)的对应于最大特征值q(G) 的一个单位特征向量X称为图G的无符号拉普拉斯主特征向量. 有
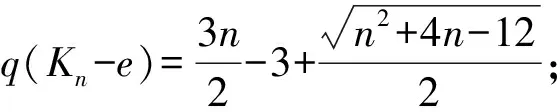
假设图G1和G2均为简单连通图. 如果图G1中的每个顶点都与G2中一样多的顶点相邻, 并且图G2中的每个顶点也都与G1中一样多的顶点相邻, 那么称图G1广义并接图G2, 或者图G2广义并接图G1. 由此得到的广义并接图记为G=G1▽G2. 特别地, 当图G1中的每个顶点都与G2中的s个顶点相邻, 而图G2中的每个顶点都与G1中的t个顶点相邻时, 把G1▽G2记为G=G1▽G2(s,t).
文中所有的符号和术语都是标准的, 可以参考文献[8].
1.2 引理
引理1假设A是一个不可约的非负矩阵,ρ(A) 是A的最大特征值. 如果A的行和分别为s1,s2,…,sn, 则
当且仅当s1=s2=… =sn,等式成立.[9]
2 主要结果
定理1假设图G是一个n阶的简单连通图, 那么2δ≤q(G) ≤ 2△, 当且仅当G是一个正则图时,等式成立.
证明:根据Q(G) 的定义, 显然矩阵中第i行的行和si等于顶点vi的度di的两倍. 根据引理1, 则有 2δ≤q(G) ≤ 2△. 证毕.
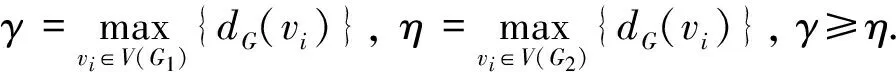
q(G)≤
(1)
当且仅当G1和G2均为正则图时,等式成立.
证明:当γ=η时, 根据引理1, 显然有不等式(1)成立, 并且当且仅当图G为正则图时,等式成立. 因此, 图G1和G2均为正则图.
当γ≠η时, 不妨假设γ>η. 将图G=G1▽G2(s,t) 的无符号拉普拉斯矩阵Q(G) 写为分块形式
其中:n=n1+n2,Q11是与G1的顶点相对应的n1×n1矩阵,Q22是与G2的顶点相对应的n2×n2矩阵. 设x是一个大于1 的实数, 令矩阵
其中:In1是一个n1×n1单位矩阵,In2是一个n2×n2单位矩阵. 记U-1Q(G)U=B, 即
显然, 矩阵Q(G)与B是相似矩阵, 它们的特征多项式的特征值均相同. 因而,q(G)=λ1(Q(G)) =λ1(B). 考虑矩阵B的n个行和r1,r2, …,rn, 可以得到:
当 1 ≤l≤n1时,

(2)
当n1+1≤k≤n时,

(3)
显然,
令
解此等式可以得到
因为γ≠η, 容易验证此时得到的x>1.故
q(G)≤
为使定理中的式(1)等号成立, 显然证明过程中所有的不等式等号均要成立. 特别地,由式(2)和(3)可知: 当1≤l≤n1时, 有dl=γ; 当n1+1≤k≤n时, 有dk=η. 因此,G1和G2都是正则图. 反之, 当G1和G2都是正则图时, 等式也成立. 证毕.
设G= (V1,V2;E) 是一个二部图, 如果对任意的u∈V1,v∈V2都有uv∈E, 则称G为完全二部图. 若|V1| =s, |V2| =t, 则记完全二部图为Ks,t. 用W1,n-1表示一个孤立点与圈Cn-1中的每个顶点相邻得到的轮图.
推论1q(Ks,t) ≤s+t.
证明:对完全二部图Ks,t, 在定理2中取值γ=s,η=t即可得. 证毕.

证明:对W1,n-1, 此时有s=1,t=n-1 并且γ= 3,η=n-1.代入定理2 即可得. 证毕.
参考文献:
[3]ZHOU B X. On the signless Laplacian spectral radius of graphs with cut vertices[J]. Linear Algebra Appl, 2010, 433(5): 928-933.
[4]LI R, SHI J S. The minimum signless Laplacian spectral radius of graphs with given independence number[J]. Linear Algebra Appl, 2010, 433(8): 1614-1622.
[5]LIU H, LU M, TIAN F. On the Laplacian spectral radius of a graph[J]. Linear Algebra Appl, 2004, 376(1): 135-141.
[6]OLIVEIRA C S, de LIMA L S, de ABREU N M M,etal. Bounds on the index of the signless Laplacian of a graph[J]. Discrete Appl Math, 2010, 158(4): 355-360.
[7]YE M L, FAN Y Z, WANG H F. Maximizing signless Laplacian or adjacent spectral radius of graphs subject to fixed connectivity[J]. Linear Algebra Appl, 2010, 433(6): 1180-1186.
[8]BONDY J A, MURTY U S R. Graph theory with applications[M]. London: The Macmillan Press LTD, 1976: 32-51.
[9]MINC H. Nonnegative matrices[M]. New York: John Wiley & Sons Inc, 1988: 132-159.
