基于响应曲面法的高速铣削Ti6Al4V表面粗糙度的预测模型与优化*
2014-04-06武文革刘丽娟
武文革 刘丽娟 范 鹏 李 波
(中北大学机械工程与自动化学院,山西 太原 030051)
本文借助Box -Behnken Design 响应曲面法,通过对难加工材料钛合金Ti6Al4V 的高速铣削试验,考察切削参数对表面粗糙度的影响规律,建立了表面粗糙度与切削用量的预测模型,并对该模型进行方差分析和适合性检验,然后利用响应曲面法建立了表面粗糙度的响应曲面及等高线图,提出了优化切削参数的方法。
1 实验方案与设计
1.1 BBD 响应曲面法
目前,对表面粗糙度的预测和优化,主要有正交试验法、响应曲面法等。常用的响应曲面法有Box-Behnken Design(BBD)响应曲面法和Central Composite Design(CCD)响应曲面法两种。Box-Behnken Design响应曲面法是可以评价指标和因素间的非线性关系的一种试验设计方法,在同等因素和水平条件下,试验次数略多于正交试验法,但与正交试验法相比,有其独特的优势。通过响应曲面法,可以通过连续性分析创建一个工艺参数与目标变量之间的响应面方程,其结果的连续性能够建立更准确的分析模型。
1.2 试验回归模型
设定切削速度Vc为x1,轴向切削深度ap为x2,径向切削深度ae为x3,每齿进给量fz为x4,同时确定加工参数的变化范围:Vc为70~110 m/min,ap为1.0~1.6 mm,ae为2.0~3.0 mm,fz为0.11~0.17 mm/齿。用z1、z0和z-1分别表示各加工参数变量的1 水平、0 水平和-1 水平,对上述4 个变量进行编码
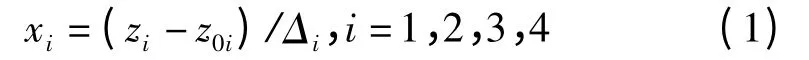
式中:xi为变量编码;zi为加工参数变量;z0i为加工参数变量的0 水平;Δi为区间变化范围,可由Δi=(z1i-z0i)/r 计算。加工参数的水平编码如表1 所示。
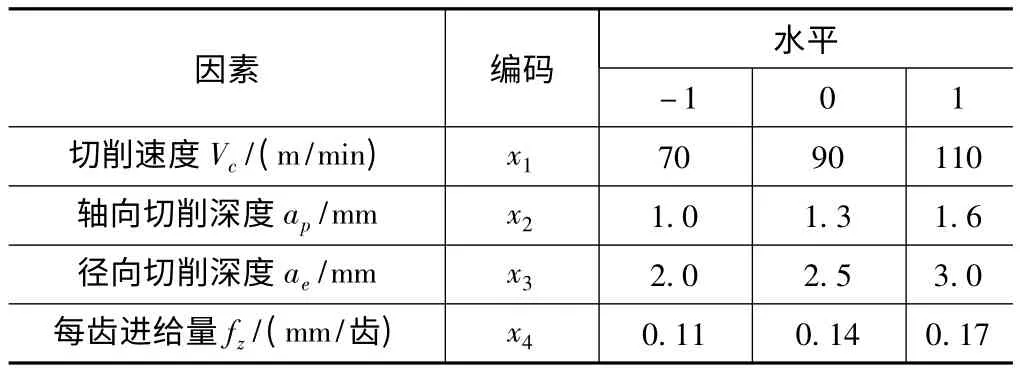
表1 切削因素水平编码表
铣削四要素都会对工件已加工表面粗糙度的大小产生影响。为了准确地了解各加工参数对表面粗糙度的影响规律,通常采用二次数学回归的方法建立表面粗糙度与加工参数之间的关系

式中:y 为表面粗糙度估计值;β0为系数的估计值;βi为线性系数;βii为二次项系数;βij为交互项系数;ε 为试验误差;xi为切削参数的编码。
试验的目的就是要获得一组最优的加工参数以便得到最佳的表面质量,但是在实际生产过程中要获得一组最优的加工参数往往又比较困难。故通过响应曲面法分析回归模型中各因素对响应值的影响,最终确定合理的水平组合使响应的预测值达到最优。
1.3 试验过程
在高速铣削加工Ti6Al4V 试验中,加工系统处于稳态,属于正常加工范畴,不研究刀具材料和参数对切削力和表面粗糙度的影响。铣刀为三齿的Y330 直柄整体硬质合金立铣刀,刀具直径d=10 mm,螺旋角30°。为便于测量粗糙度,进行平面铣削加工,工件材料为Ti6Al4V(调质、硬度28~30 HRC),工件尺寸为120 mm ×70 mm ×35 mm。铣削方式为逆铣,采用乳化油冷却。表面粗糙度测量采用的JB -5C 粗糙度轮廓仪。采用HCZK1340 数控机床,主轴最高转速8 000 r/min,机床功率为10 kW,最大进给速度为10 m/min(空行程),如图1 所示。

2 试验结果及分析
通过29 次的高速铣削试验并测量每次试验的表面粗糙度,结果如表2 所示。将所得的试验数据采用Design Expert 8.05 软件进行多元回归拟合,得到表面粗糙度y 对切削速度、轴向切削深度、径向切削深度和每齿进给量的二次多项回归方程:

其中,y 为表面粗糙度的预测值,x1、x2、x3、x4分别为切削速度、轴向切削深度、径向切削深度和每齿进给量的编码值。

表2 试验结果
对得到的二次多项回归模型进行方差分析,结果如表3 所示。由表3 可知,回归模型P <0.000 1,表明响应回归模型达到了极显著水平,失拟项P=0.111 2>0.05,表明失拟不显著,模型的校正确定系数R2=0.945 0,说明该模型能解释94.50%响应值的变化,该模型拟合程度良好,能较好地反映因素和指标间的关系。模型响应值的变异系数CV 值为5.73%,较低,表明实验操作是可信的,因此用此模型可以对工件表面粗糙度进行分析和预测。此外,还可以看出各个因素对表面粗糙度影响的大小顺序为:每齿进给量(x4)>切削速度(x1)>轴向切削深度(x2)>径向切削深度(x3)。
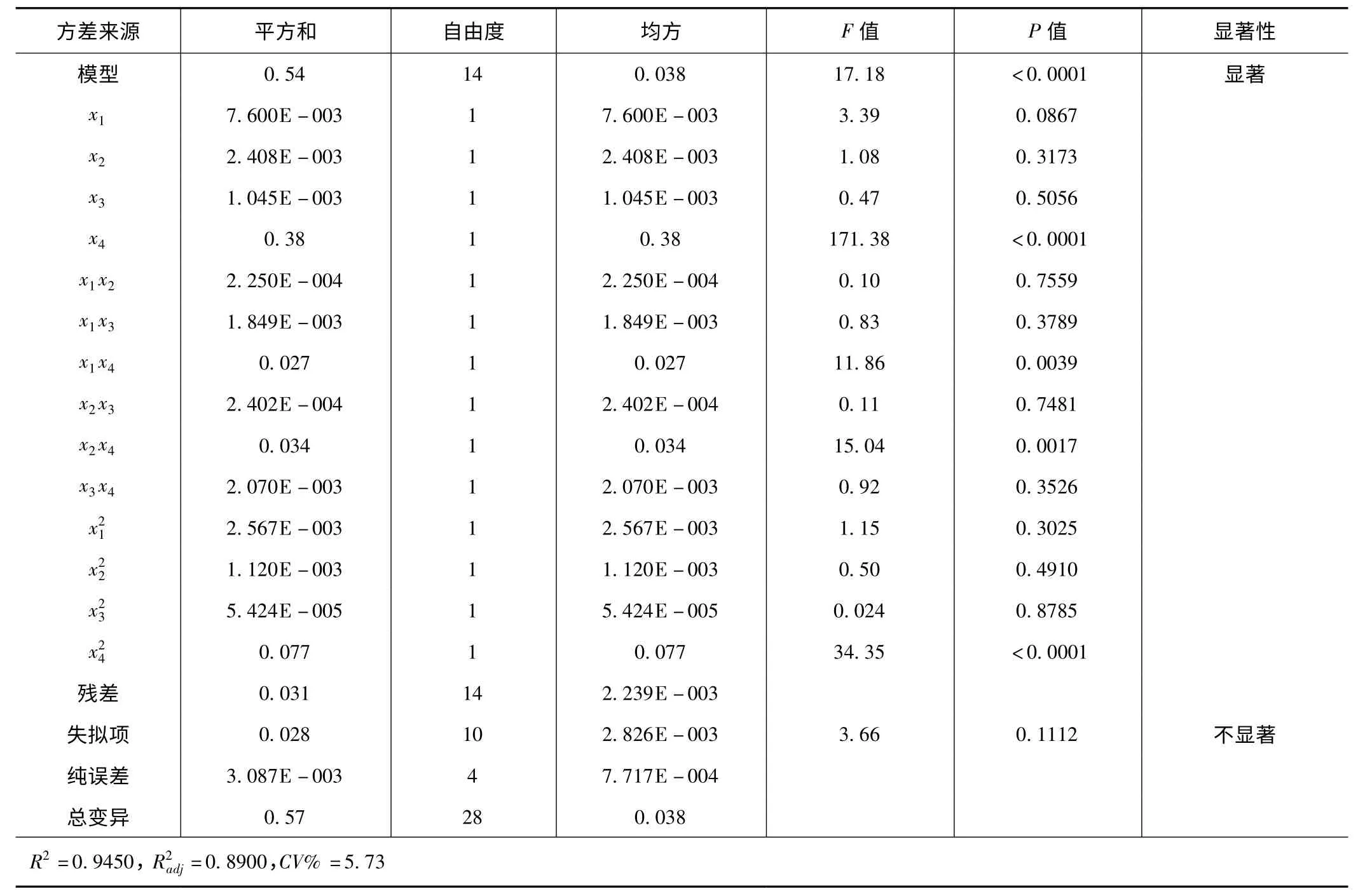
表3 回归模型的方差分析
3 响应曲面分析
对表2 试验结果的数据进行二次多元回归拟合,所得到的二次回归方程的响应面及其等高线图如图2~7 所示。根据响应曲面及其相应的等高线图可评价切削参数对表面粗糙度的两两交互作用,以及确定各因素的最佳水平范围。
图2 为径向切削深度和每齿进给量为0 水平时,切削速度和轴向切削深度的响应曲面和等高线图。如图所示响应曲面十分平整,等高线曲率半径小,表明切削速度和轴向切削深度对表面粗糙度的交互作用不明显。随着切削速度和轴向切削深度的增大,表明粗糙度Ra值增大不显著。
图3 为轴向切削深度和每齿进给量为0 水平时,切削速度和径向切削深度的响应曲面和等高线图。如图所示响应曲面缓慢上升,等高线曲率半径较大,表明切削速度和径向切削深度对表面粗糙度的交互作用较明显。随着切削速度和径向切削深度的增大,表明粗糙度值增大较显著。
图4 为径向切削深度和轴向切削深度为0 水平时,切削速度和每齿进给量的响应曲面和等高线图。如图所示响应曲面上升很明显,等高线曲率半径很大,表明切削速度和每齿进给量对表面粗糙度的交互作用很明显。随着切削速度和每齿进给量的增大,表明粗糙度值增大很显著。
图5 为切削速度和每齿进给量为0 水平时,轴向切削深度和径向切削深度的响应曲面和等高线图。如图所示响应曲面很平缓,等高线曲率半径很小,表明轴向切削深度和径向切削深度对表面粗糙度的交互作用很不明显。随着轴向切削深度和径向切削深度的增大,表明粗糙度值变化不显著。
图6 为切削速度和径向切削深度为0 水平时,轴向切削深度和每齿进给量的响应曲面和等高线图。如图所示响应曲面上升非常明显,等高线曲率半径非常大,表明轴向切削深度和每齿进给量对表面粗糙度的交互作用非常明显。随着轴向切削深度和每齿进给量的增大,表明粗糙度值显著增大。


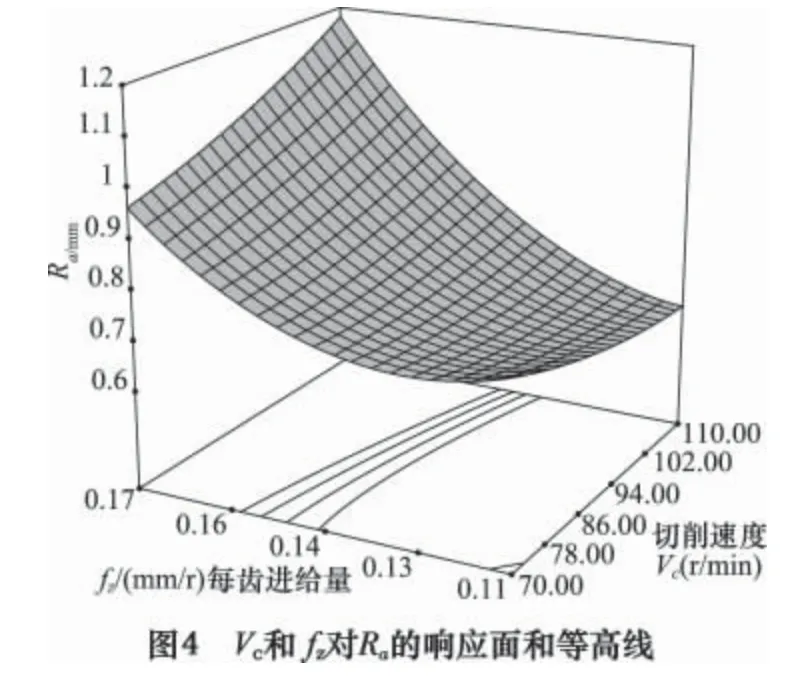
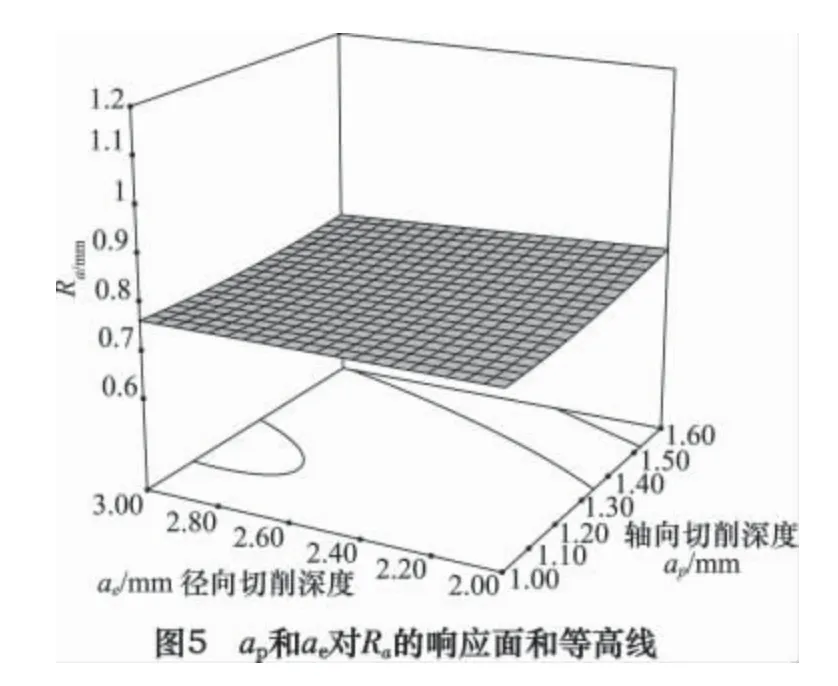
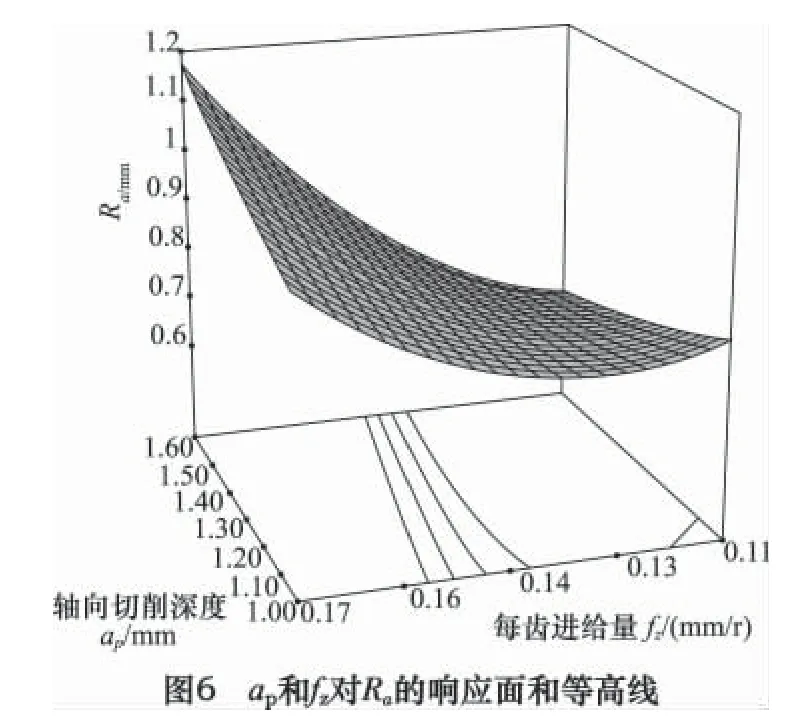

图7 为轴向切削深度和轴向切削深度为0 水平时,径向切削深度和每齿进给量的响应曲面和等高线图。如图所示响应曲面缓慢上升,等高线曲率半径较大,表明径向切削深度和每齿进给量对表面粗糙度的交互作用较明显。随着径向切削深度和每齿进给量的增大,表明粗糙度值增大较显著。
4 结语
(1)通过对表面粗糙度的建模及各因素的效应分析,表明了每齿进给量对表面粗糙度的影响最大,其次是切削速度、轴向切削深度和径向切削深度。
(2)对试验结果的数据进行二次多元回归拟合,得到二次回归方程的响应面及其等高线图。根据响应曲面及其相应的等高线图评价了切削参数对表面粗糙度的两两交互作用,可确定出各因素的最佳水平范围。
[1]Suresh P V S,Venkateswara R P,Deshmukh S G.Agenetic algorithmic approach for optimization of surface roughness prediction model[J].International Journal of Machine Tools & Manufacture,2002,42 (6):675 -680.
[2]Yusuf Sahin,Riza Motorcu A.Surface roughness model for machining mild steel[J].Materials and Design,2005,26(4):321 -326.
[3]李学崑,朱天行,李峰,等.基于响应曲面法的超硬磨粒姿态对于微切削过程影响的研究[J].金刚石与磨料磨具工程,2013,33(2):1 -13.
[4]宿程远,李伟光,王 勇,等.Box -Behnken 响应曲面优化铁炭微电解降解结晶紫[J].环境工程学报,2013,7(1):7 -13.
[5]贾旭.黄铜微铣削工艺参数对表面粗糙度影响规律及预测模型研究[D].大连:大连理工大学,2012.
