基于MIV与RBF神经网络的滚珠丝杠故障诊断*
2014-04-06温国强谭继文
温国强 文 妍 谭继文
(青岛理工大学,山东 青岛 266033)
滚珠丝杠是数控机床中最常使用的关键传动元件,具有高精度、可逆性和高效率的特点[1]。滚珠丝杠若出现故障,将会直接影响到数控机床的加工精度,造成产品质量下降甚至报废,损失严重。因此,若能在滚珠丝杠故障形成早期进行正确及时的诊断,对其生产效率与产品质量的提高大有裨益。
在传统诊断方法中,通常是对原始故障信号进行特征提取后,将所有特征值作为传统BP 神经网络或者支持向量机的输入参量进行模式识别。这种方法输入参量多、诊断过程复杂,同时,由于BP 网络容易陷入局部极小值,而且收敛速度相对较慢或无法收敛,诊断精度相对较低。本文引入平均影响值(MIV)方法对故障特征进行筛选处理,去除冗余特征,将剩余特征作为故障识别的输入参量;基于具有逼近精度高、无局部极小问题且收敛速度快等特点的径向基(RBF)神经网络建立了数控机床滚珠丝杠故障识别模型,有效提高了故障诊断精度和速度,效果良好。
1 MIV 算法
1.1 平均影响值(MIV)
平均影响值(MIV,Mean Impact Value),是一种目前被认为是在神经网络中评价变量相关性的最好指标之一[2]。该算法可用于确定输入变量对输出变量的影响大小,其符号代表相关的方向,绝对值代表影响的大小。
1.2 计算思想[3]
(1)用原始样本S 对BP 神经网络进行训练,并对训练集S 进行回归预测;
(2)在网络训练结束后,将训练样本S 中每一自变量在其原值的基础上分别加、减10%构成两个新的训练样本S1 和S2;
(3)利用构建好的BP 网络,对样本Sl 和S2 分别进行仿真,得到两个仿真结果Ml 和M2;
(4)求出Ml 和M2 的差值,即为变动该自变量后对输出产生的影响变化值(简称W);
(5)将W 按观测例数平均得出该自变量对于因变量的平均影响值MIV,同理可计算出各个自变量的MIV 值;
(6)根据MIV 绝对值的大小为各自变量排序,得到各自变量对网络输出影响相对重要性的位次表,从而判断出输入特征对于网络结果的影响程度,即实现了变量筛选。
2 RBF 神经网络
2.1 RBF 网络
RBF 神经网络是1985 年由Powell 提出的多变量差值的径向基函数(Radial Basis Function,简称RBF)方法。该网络是一种性能优良的前馈型神经网络,具有唯一的最佳逼近特性,且无局部极小问题存在[4]。其结构与多层前向网络相似,是三层的前向网络,由一个输入层、一个隐含层、一个输出层组成。
2.2 RBF 网络算法
学习算法具体步骤如下[5]:
步骤1:基于K-均值聚类方法求取基函数中心c。
(1)将网络进行初始化设置:随机选取h 个训练样本作为聚类中心ci(i=1,2,…,h)。
(2)利用最近邻规则将输入的训练样本集合进行分组:按照xp与中心ci之间的欧式距离将xp分配到输入样本的各个聚类集合vp(i=1,2,…,h)中。
(3)聚类中心作重新调整:对每个聚类集合vp中的训练样本求取平均值,构成新的聚类中心ci,如果ci没有改变,则此时的ci就是RBF 神经网络最终的基函数中心,否则返回(2),进行下一轮的中心求解。
步骤2:求解方差σi。
选取高斯函数作为该RBF 神经网络的基函数,方差σi可由下式求解:
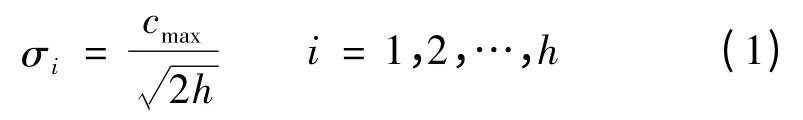
式中,cmax是所选取中心之间的最大距离。
步骤3:求取隐含层和输出层之间的权值。
运用最小二乘法可直接计算出隐含层到输出层之间神经元的连接权值,计算公式如下:
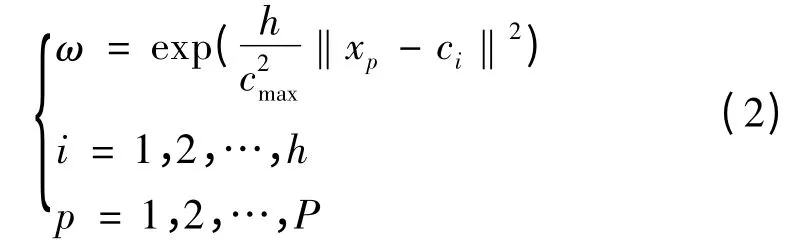
3 滚珠丝杠故障诊断实例与建模
3.1 信息采集
将加速度传感器布置于丝杠两端轴承座处,采集工作状态下的滚珠丝杠振动信号。为获取较全面的故障信息,采用3 个传感器测量X(径向)、Y(轴向)、Z(径向)3 个方向的信号,如图1 所示。

本实验用正常丝杠、滚珠磨损、滚道磨损及丝杠弯曲4 种状态试件,检测每种试件运行时20 组振动信号。取出每种状态前16 组作为训练集,剩余4 组作为测试集。
3.2 特征提取
(1)时域特征:标准差、均方根、峭度、峰值、峰度、偏斜度。
(2)频域特征:能量。依据EMD 方法适合于分析非线性、非平稳信号序列的特性[6-7]。本例借该法对采集的振动信号进行经验模态分解,并提取前8 个本征模函数(IMF)的能量值C 作为频域特征。
本实例分别提取X、Y、Z 三向振动信号的前8 个IMF 能量和6 个时域特征指标,总共42 类特征值。
3.3 特征筛选
3.3.1 BP 网络设计
由于本例中MIV 依附于BP 网络训练进行筛选,这里首先需要对BP 网络进行设计。
(1)输入层:等于特征值个数为42;
(2)输出层:利用1 个节点输出值表示4 种故障状态,期望输出结果为:
正常为“1”、滚珠磨损为“2”、滚道磨损为“3”、丝杠弯曲为“4”;
(4)学习速率
通常情况下倾向于选取较小的学习速率以保证系统的稳定性。学习速率的选取范围在0.01~0.8 之间[8]。结合本实验进行多次对比分析,选取学习速率为0.1 可达较好效果。
(5)期望误差
通常期望误差设定值越小,网络诊断精度越高,但若太小会使网络训练时间过长甚至不能收敛。经多次试验,选取期望误差为0.001 较为合适。
3.3.2 特征量筛选结果
依据MIV 算法得到各个特征的平均影响值(MIV),依次填入表格并进行位次排序,见表1。由于表格格式限制,只列出排位前14 的特征值。
参照表1,选取与结果正相关且绝对值较大的前10 个特征作为新的特征集组合,按由大到小排序分别是:C1X、C1Z、C3X、峰度Y、C5Z、C2X、C1Y、标准差X、C2Y、标准差Y。
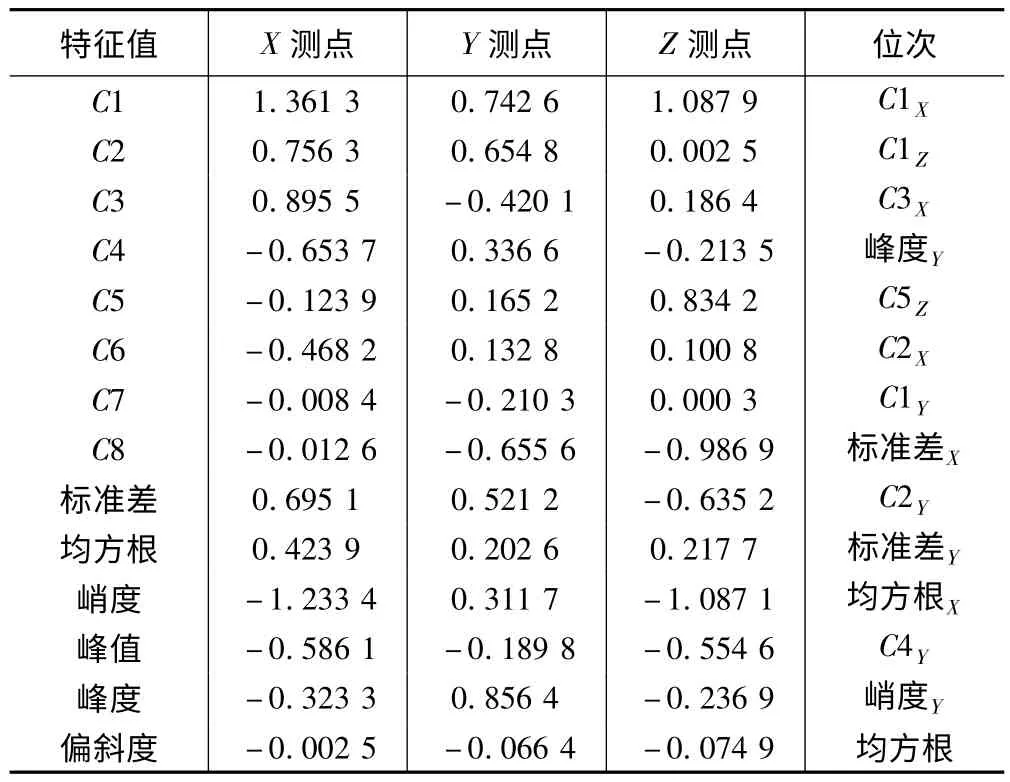
表1 平均影响值MIV
3.4 模式判别
3.4.1 建立RBF 神经网络
调用Matlab 工具箱中newrb 函数实现对RBF 网络进行的设计。newrb 函数格式如下:
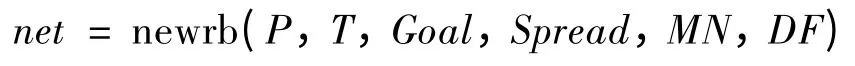
P 为输入向量:对应经MIV 筛选后的10 类特征量。T 为目标向量:输出层节点数,利用4 个节点输出值表示4 种故障状态,期望输出结果为:正常[1,0,0,0]、滚珠磨损[0,1,0,0]、滚道磨损[0,0,1,0]、丝杠弯曲[0,0,0,1]。Goal 为均方误差,本例取作0.001;Spread 为径向基函数的分布密度,默认为1。MN 为神经元的最大数目。DF 为两次显示之间所添加的神经元数目,默认为1。
3.4.2 不同诊断模式对比分析
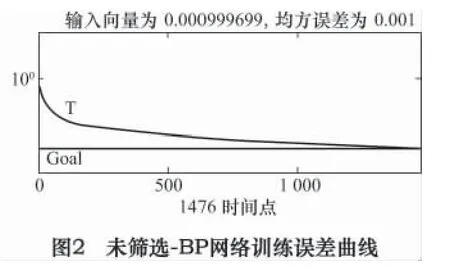
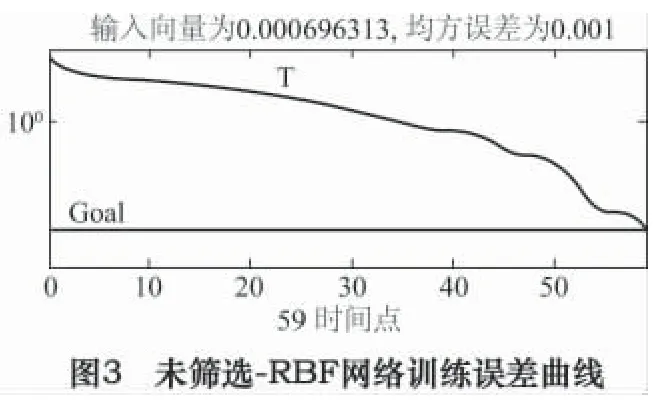
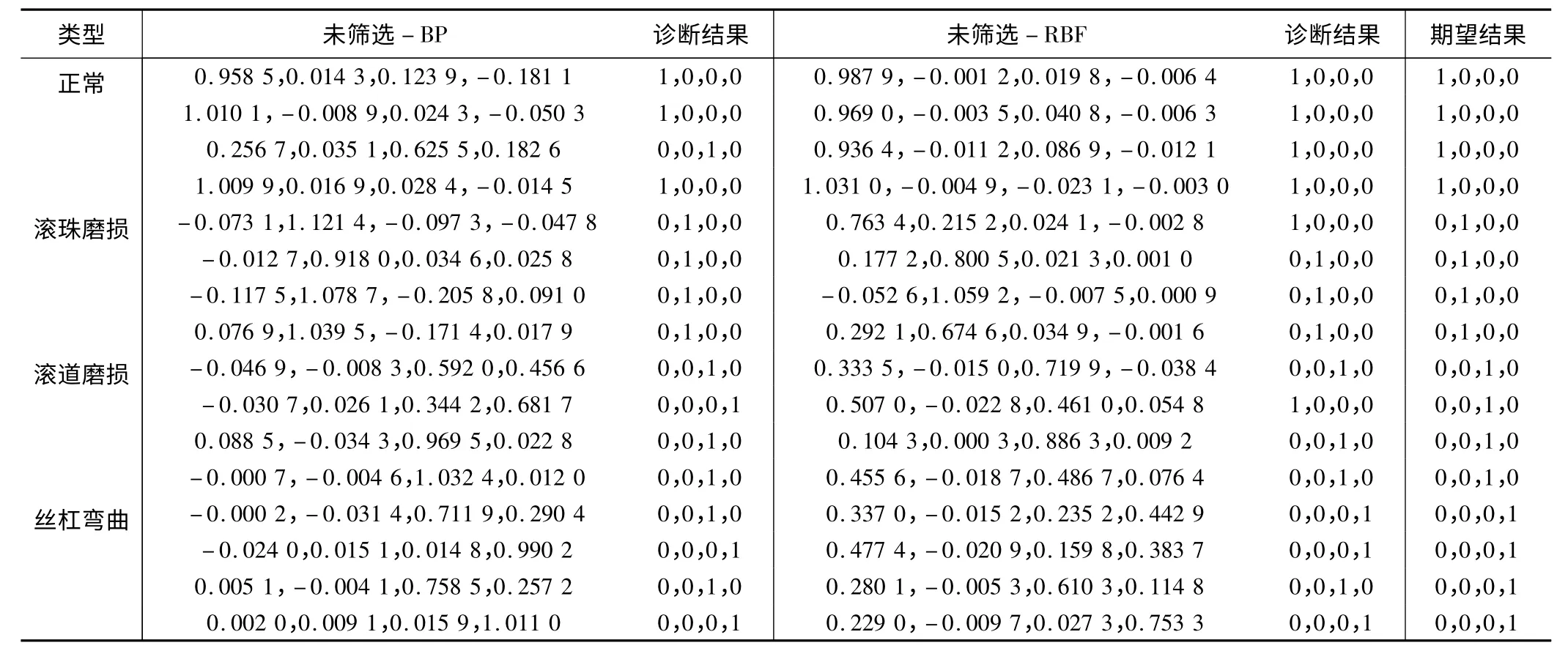
表2 未筛选-BP、未筛选-RBF 实际输出及诊断结果
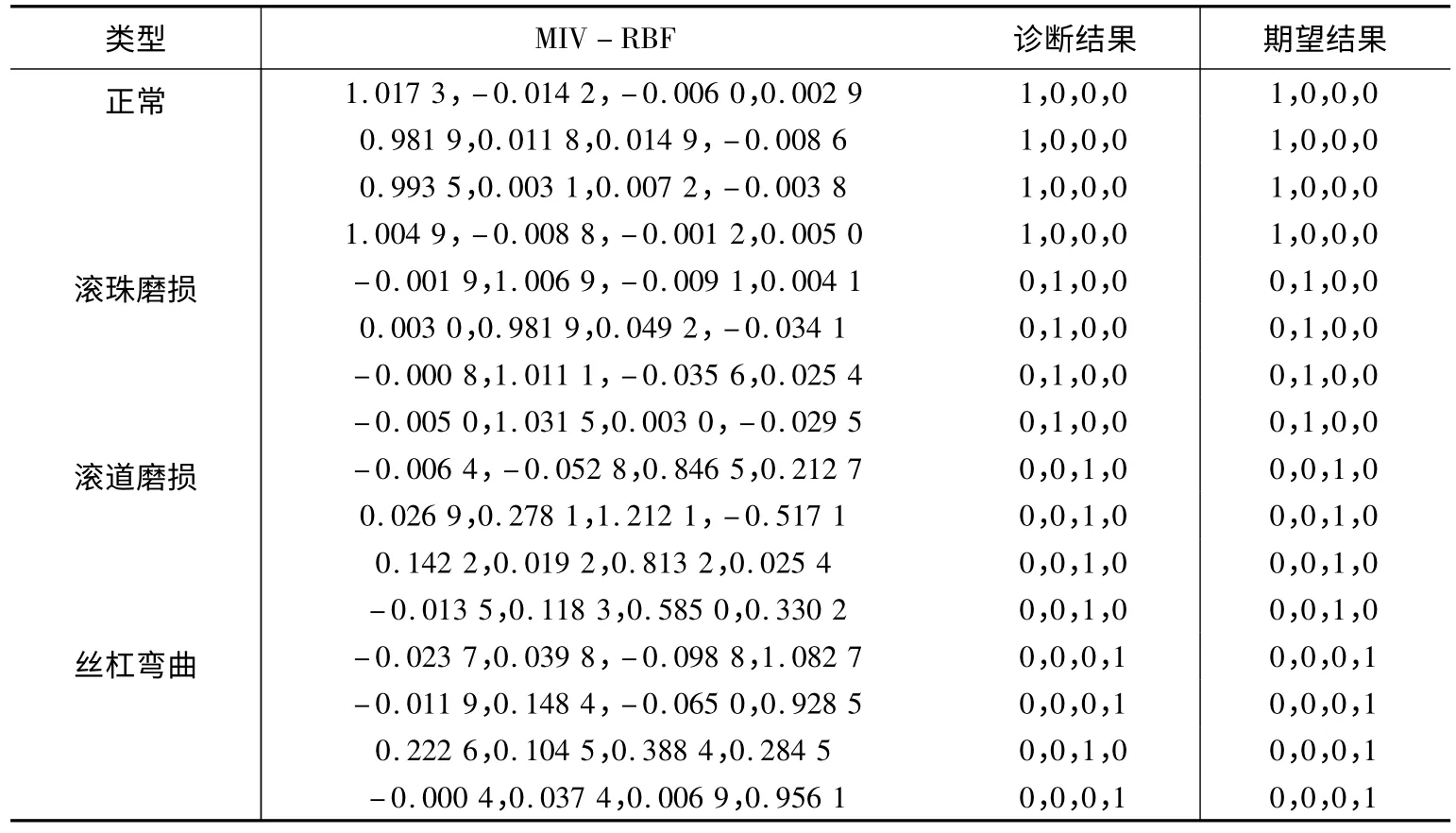
表3 MIV-RBF 实际输出及诊断结果
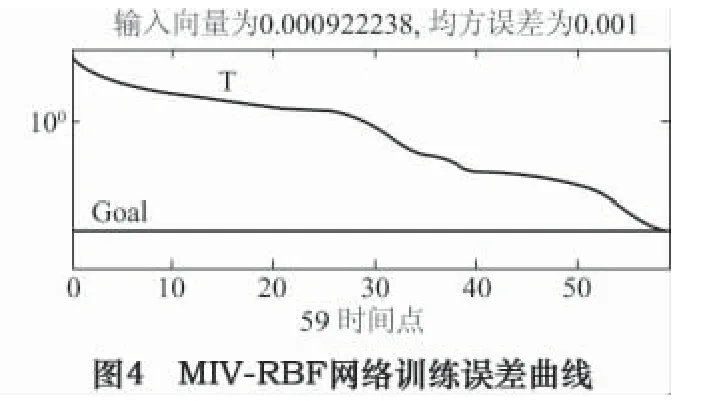
对“未筛选-BP”、“未筛选-RBF”、“MIV -RBF”三种模式训练与诊断结果进行分析,得到网络训练误差曲线如图2、图3、图4 所示;网络实际输出及诊断结果见表2、表3。
在BP 网络、RBF 网络的输入层、隐含层、输出层、期望误差一致的情况下,通过对3 种诊断模式的训练与诊断结果进行对比分析,得出结论汇总表,见表4。由表4 可得:

表4 汇总
(1)RBF 网络相对于BP 网络,能使用较少的训练步数,在较短的训练时间内达到收敛,完成训练;同时具有较高的正判率。
(2)基于MIV 筛选后的RBF 网络诊断相对于未筛选的RBF 网络,训练速度相差不大,但是正判率有明显地提高。
4 结语
为了实现对滚珠丝杠的故障诊断,本文提出了一种基于MIV 与RBF 神经网络的故障诊断方法。该方法首先通过MIV 算法对获得的特征进行筛选处理,保留对诊断结果影响较大的特征构成新的特征集合。将新的特征集作为网络输入,构建RBF 神经网络以实现诊断功能,并与传统诊断方法进行比较,验证了该方法在滚珠丝杠故障诊断中的可行性和优越性。
[1]王植,殷爱华.滚珠丝杠导程误差分析与计算机辅助诊断研究[D].南京理工大学,2004:1 -3.
[2]周莹,程卫东.基于MIV 特征筛选和BP 神经网络的滚动轴承故障诊断技术研究[D].北京:北京交通大学,2011:25 -27.
[3]王紫微,叶奇旺.基于神经网络MIV 值分析的肿瘤基因信息提取[J].数学的实践与认识,2011,41(14):47 -57.
[4]史峰,王小川,郁磊,等.MATLAB 神经网络30 个案例分析[M].北京:北京航空航天大学出版社,2010:65 -72.
[5]郭秀容,陆怀民.RBF 神经网络在电喷发动机故障诊断中的应用研究[D].哈尔滨:东北林业大学,2005:9 -12.
[6]Huang N E,Shen Z,Long S R,et al.The empirical mode decomposition and the hilbert spectrum for non -linear and non -stationary time series analysis[C].Proc.R.Soc .Lond.A,1998,454:903 -995.
[7]Shen F,Zheng M,Shi D F,et al.Using the cross -correlation technique to extract modal parameters on response-only data[J].Journal of Sound and Vibration,2003,259(5):1163 -1179.
[8]王凡重,田慕琴.基于小波神经网络和支持向量机的电机故障诊断与研究[D].太原:太原理工大学,2011:46 -47.
