区间数比较可能度在新兴产业评价中实例研究

谢丹丹，刘 珊，贺 菲

(1.江西省科技发展研究中心，江西 南昌330046;2.江西科技师范学院数学与计算机科学学院，江西 南昌330013; 3.江西财经大学信息管理学院，江西 南昌330013;)

1 区间数的定义

先给出区间的运算法则:

2 区间数比较的可能度公式

定义1［3］:当和同时为区间数或者有一个为区间数时，设=［aL，aU］，=［bL，bU］。且记la=aU－aL，lb=bU－bL，则称

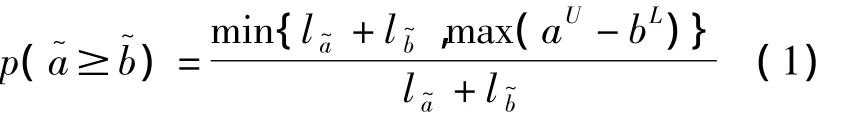
该定义作为区间数比较的可能度常用公式，形式简洁，便于对以区间数形式给出的评价项目进行比较计算，较好地解释了人们在思维中出现的模糊性、不确定性与思维的复杂性，在实际中有广泛的运用。不难看出，公式(1)，默认区间=［aL，aU］中各点的取出是均匀的［4］，但在实际的群体决策问题中，许多评价信息常常有可能出现在一定的区间范围内对同一区间内的不同点有偏好，比如更加倾向于区间中间的点(决策者比较中庸)，或者倾向于区间两头的点(决策者比较极端)，或者更一般的情况是决策者对于区间中的点的选择可以以一定的概率分布的形式表达。基于上述情况，为了充分考虑实际中区间=［aL，aU］中各点的取出不均匀的情况，将概率密度函数的概念引入区间数比较的可能度公式。

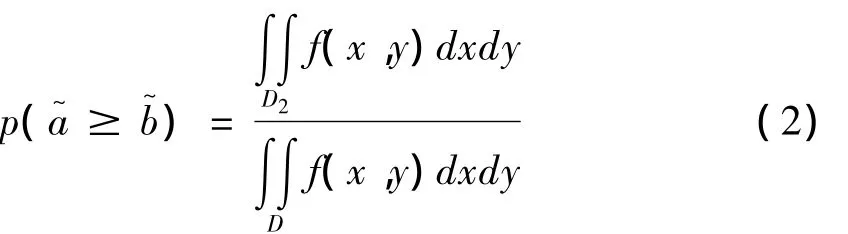
特殊地，若∀x∈［aL，aU］与∀y∈［bL，bU］相互独立，则有

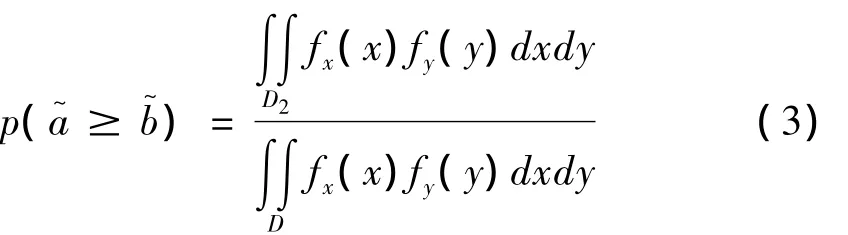
(2) 若bU≤aL，则p(≥)=1，

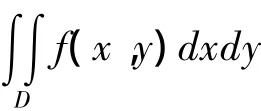
(3)若aU≥bL，则p(≥)=0，

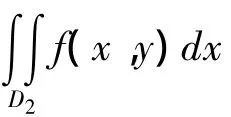
3 常见概率分布在区间数比较的可能度公式上的运用

3.1 均匀分布

∀x∈［aL，aU］，∀y∈［bL，bU］，若x，y分别服从［aL，aU］和［bL，bU］上的均匀分布，即x∈U［aL，aU］，y∈U［bL，bU］，且x与y相互独立，则

其中，

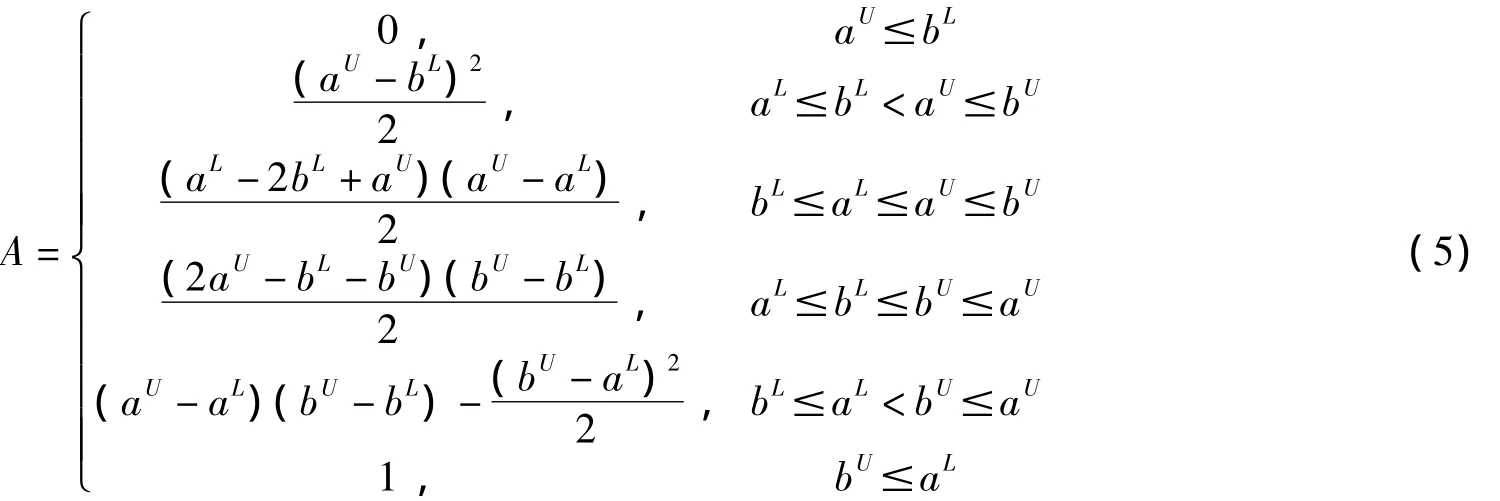
根据计算结论(4)，可以证明下列结论均成立

3.2 正态分布

∀x∈［aL，aU］，∀y∈［bL，bU］，若x，y分别服从参数为(μ1，)和(μ2，)上的正态分布，即x∈N(μ1，)，y∈N(μ2，)，则

根据经验，在实际计算过程中，该区间数可能度计算公式中的μ1，μ2可取μ1特别地若x与y相互独立，则ρ=0［5］。由于的原函数不是初等函数，故在实际计算过程中可以采用蒙特卡洛法进行计算机仿真模拟计算，通过MATLAB可以得出计算结果。

4 区间数可能度公式的实例研究

上述区间数可能度公式由于概率密度的引入，一般要求∀x∈［aL，aU］为连续型随变量，但在群体决策中，有些评价数据信息只集中在区间［aL，aU］上的某几个点上，如满意度信息，一般只集中在［十分满意满意不满意非常不满意］等几个离散点上，也可以仿照定义2，对各类情况进行定义。

考虑一个新兴产业企业科技研发(R＆D)投入评估问题。通常一些企业采用技术人员数u1、资金投入u2和专利数u3作为评估指标。

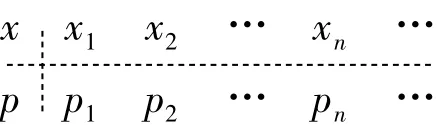
的概率分布取［aL，aU］中的x1，x2，…，xn等离散数值，∀y∈［bL，bU］，y服从概率密度函数f(x，y)，x与y相互独立，则

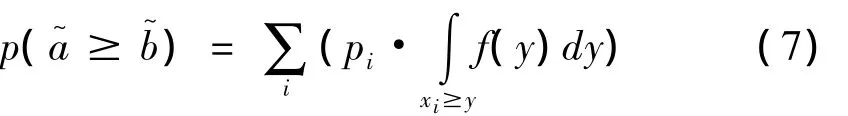
实例1:新兴企业科技研发(R＆D)投入评估中，企业甲的技术人员数ux以ux=［20 30］区间数这种不确定形式给出，且有

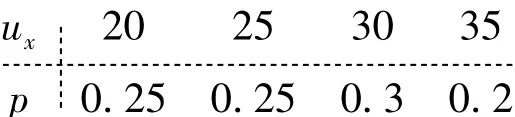
企业乙的技术人员数uy以uy=［30 50］区间数这种不确定形式给出，且有

所以ux≥0.205uy，ux≤0.795uy。

实例2:新能源企业甲的科研资金投入ux以ux=［3 9］区间数这种不确定形式给出且可能的密度函数为均匀分布，新能源企业乙的科研资金投入uy以uy=［5 8］区间数这种不确定形式给出且可能的密度函数为均匀分布，则由公式(5)得，

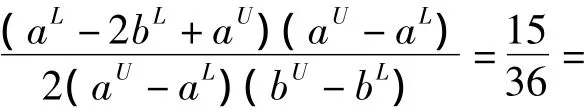
的概率分布取［bL，bU］中的y1，y2，…，yn等离散数值，如果x与y相互独立，则

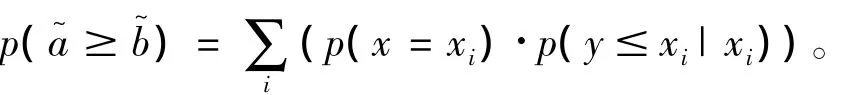
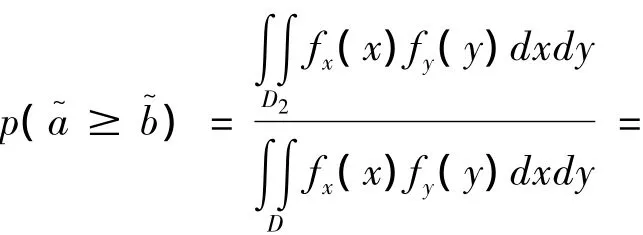
所以

［1］ 徐泽水.不确定多属性决策方法及应用［M］.北京:清华大学出版社，2004:105－110.

［2］ 同济大学数学教研室.高等数学［M］.北京:高等教育出版社，2004.

［3］ 徐泽水，达庆利.区间数排序的可能度法及其应用［J］.系统工程学报，2003，18(1):67－70.

［4］ 刘次华.概率论与数理统计［M］.武汉:华中科技大学出版社，2009:46.

［5］ 胡运权.运筹学教程［M］.北京:清华大学出版社，2007:279.

［6］ 谢乃明，刘思峰.考虑概率分布的灰数排序方法［J］.系统工程理论与实践，2009，(4):171－175.