基于邻域粗糙集的入侵检测集成算法

魏 峻

WEI Jun

陕西理工学院 数学与计算机科学学院，陕西 汉中 723000

School of Mathematics and Computer Science,Shaanxi University of Technology,Hanzhong,Shaanxi 723000,China

1 引言

入侵检测是一种重要的主动网络安全技术，可有效发现来自网络外部与内部误操作引起的攻击，它与防火墙等静态安全技术配合使用，有效提高网络的安全性。

入侵检测领域获得的数据具有自身的特点：（1）非线性特点；（2）高维数特点；（3）高噪声与高冗余特点；（4）连续型特点。以上的这些特点导致了通常的模式分类算法不能有效地应用于入侵检测领域。针对数据非线性以及复杂性的特点，使得数据往往并不服从一些已知分布，这就使得传统的分类方法并不能很好地应用于该领域，机器学习方法通过对样本的训练来掌握数据背后所掩盖的规则，因而被广泛应用于入侵检测领域。其中神经网络和支持向量机是两种常用的对非线性问题非常有效的处理方法。但是神经网络本质是一种局部搜索方法，易陷入局部极小化，收敛速度较慢及拓扑结构难确定等不足。而支持向量机是建立在统计学习理论基础上，以结构风险最小化为原则的机器学习方法，具有结构简单、全局优化、收敛速度快及泛化性能好的优点，能很好地解决非线性问题。陈光英等[1-4]采用SVM进行入侵检测，获得了较好效果，显示了SVM优于其他分类算法的性能。但是支持向量机的分类性能往往受到参数影响，不同的参数所获得的分类性能也不一样，单个分类器所获得的结果易陷入局部最优，这就使得这种单一分类器存在可靠性与稳定性差的问题，为解决这个问题，引入了集成技术[5-8]。集成技术是使用一系列分类器进行学习，并使用某种规则把各分类结果进行合成从而获得比单个分类器有更好学习效果的一种机器学习方法。采用多分类器集成，各个基分类器可能在解空间的不同局部区域进行搜索，其最终合成的搜索结果往往是共同趋于某个实际目标，既提高了算法的稳定性与可靠性，又增强了算法的泛化性能。

由于入侵检测数据具有高维性，且含有大量的噪声与冗余属性，这些属性的存在会降低检测的效果和效率，所以属性约简是提高入侵检测性能的有效途径。其中粗糙集是一种常用且有效的属性约简方法。蔡忠闽等[9-13]把粗糙集引入到入侵检测中，进一步提高检测效果。但传统粗糙集不能直接处理连续型数据，需要对连续型数据离散化，这一处理过程必然会带来信息丢失，影响检测效果。邻域粗糙集（Neighborhood Rough Set）[14-18]是对经典粗糙集理论的改进，它能够直接处理连续型数据，而不需要事先对连续数据进行离散化处理，这就避免了离散化过程带来的信息损失问题，使获得的属性子集具有更强的泛化性能。

基于以上分析，首先采用Bagging算法[19]进行训练样本扰动，然后利用具有不同半径的邻域粗糙集模型进行特征扰动实现属性约简，这样既能增大训练子集的差异性，又能获得具有较高精度的训练子集，然后在这些训练子集上训练支持向量机基分类器，最后根据各基分类器的检测精度进行加权集成。通过在KDD99数据集上进行仿真实验来验证算法的有效性和实用性。

2 邻域粗糙集模型

粗糙集[9]是一种刻画不完整性和不确定性的数学工具，能有效地分析不精确、不一致、不完整等各种不完备的信息，还可以对数据进行分析和推理，从中发现隐含的知识，揭示潜在的规律。其中，粗糙集在属性约简方面有着重要的应用。但是粗糙集理论只能针对离散数据进行处理，所以对于连续型数据首先要进行离散化，即使采用较好的离散化方法，也不能避免离散化过程所带来的信息损失。邻域粗糙集[14-18]是一种对于连续性的数据可以直接处理的方法，它不需要事先对连续型数据进行离散化处理，可直接用于知识约简等问题。因此，为保证入侵检测的准确性，本文采用邻域粗糙集方法进行属性约简。

邻域决策系统 NDT=＜S，A=G∪D，V，f＞，其中 S={s1,s2,…，sm}是样本集，称为样本空间。G={g1,g2,…，gn}是属性集，称为条件属性。D={L}是一个输出特征变量，称为决策属性，L表示所属样本的标记。Va表示属性a∈G∪D的值域，f是一个信息函数，可表示为f:S×(G∪D)→V ，其中。

如果 ∀si∈S且 B∈G，样本 si在 B中的邻域为δB(si)，则 δB(si)={sj|sj∈S，ΔB(si，sj)≤δ}，其中 δ是一个预设的阈值，ΔB(si，sj)是在B中的一个测度函数。设s1和 s2是 G={g1，g2，…，gn}中的两个样本，f(s，gi)表示样本s在第i维属性gi的值，则Minkowsky距离可定义为

给定邻域决策表 NDT，X1，X2，…，Xc是具有决策属性类别值 1到 c的样本集，则，所以 X1，X2，…，Xc是 S 的一个划分，表示由属性子集B⊂G产生的包括样本xi的邻域信息粒度，则决策属性D关于属性子集B的下近似和上近似表示为：

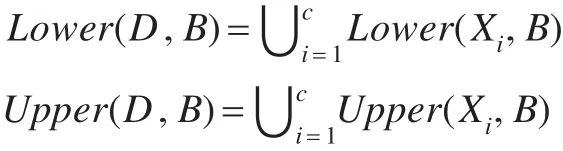
设a∈B，则属性的重要度定义为：

邻域粗糙集属性约简算法伪代码：

输入：NDT=＜S，A=G∪D，V，f＞、邻域半径 δ

输出：约简子集red

（1）∀a∈G，计算邻域相关度；

（2）令 red=∅；

（3）对每一个 ai∈G-red ，计算

（4）选择 ak，使其满足

（5）若 SIG(ak，D，red)＞0，则 red=red∪ak，且返回到（3）继续执行；否则输出约简子集red。

3 算法思想与框架

多分类器集成是提高分类性能的有效方法，为获得理想的集成效果，必须保证各基分类器间有足够的差异性，且分类器之间能形成互补，所以基分类器之间的差异性是集成的关键之一。要增强分类器之间的差异性，产生差异性较大的训练子集是一种有效的方法。Bagging[19-21]是基于有放回重采样技术的一种集成算法，从原始训练集中随机抽取若干样本组成训练子集，训练子集的规模与原始训练集相当，训练样本允许重复选取。这样原训练集中某些样本可能在新的训练子集中出现多次，而另外一些样本可能一次也不出现，由此可以产生具有较大差异性的训练子集。

利用Bagging技术产生的每个bootstrap训练子集，由于大量噪声及冗余属性，采用具有不同半径的邻域粗糙集进行属性约简，一方面可以剔除噪声和冗余属性，使获得的分类器具有较高的精度；另一方面使用不同半径的邻域粗糙集对bootstrap训练子集进行约简，相当于将训练子集映射到不同的特征空间，这样进一步加大了训练子集的差异性，从而使得最终获得的分类器具有较高的精度和较大的差异性。

基分类器合成也是影响集成性能的重要因素，投票法是目前最常用且容易理解的一种合成方法，主要有大多数投票和加权投票两种。大多数投票可视为加权投票法中所有基分类器权值均等的特殊情况。如果采用大多数投票方法，当出现两个或两个以上类标签同时得到最大投票数时，就会产生决策冲突，因此需要一些方法来作为冲突消解策略，比如基于阈值的较多数投票法。大量研究表明，大多数投票是最常用的集成策略，但并不是最好的，因为它获得的结果不可能优于任何一个基分类器。而加权投票法能够获得比大多数投票法更好的识别率。基分类器的权重分配与基分类器在训练集上的预测精度相关联的，设第i个分类器权重为bi，则有成立时，其最终决策为样本属于第k类。其中，pi为第i个分类器在训练集上的预测精度，采用文献[22]中的权重计算方法，且充分使用各分类器的先验信息，可使得集成系统的识别精度最大化。

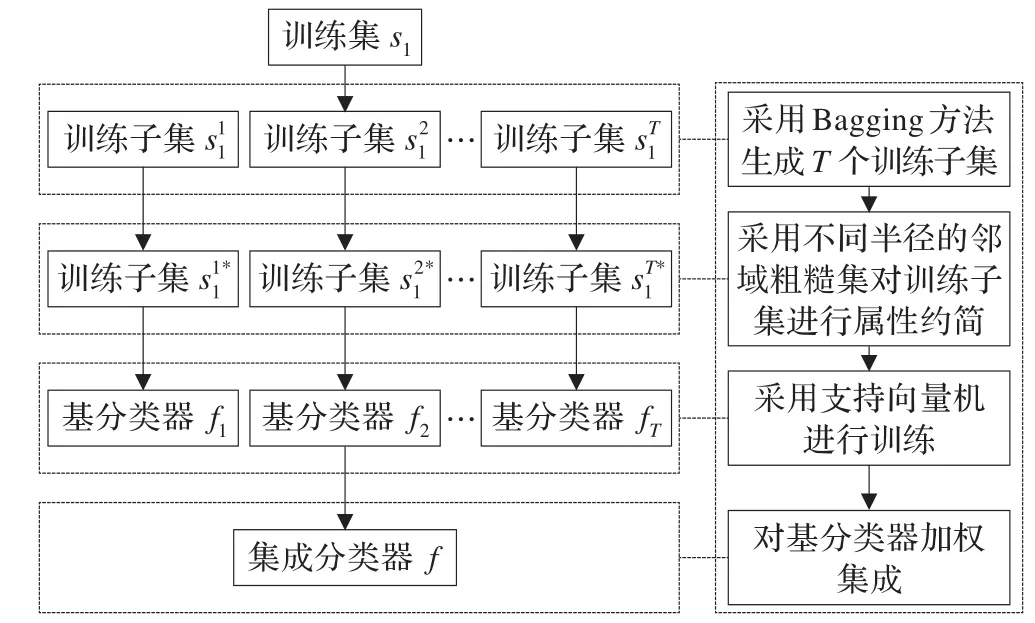
图1 算法框架图

4 算法步骤

输出：集成分类器 f。

步骤1 fori=1:T

（1）从训练集s1中进行有放回重采样生成bootstrap训练子集

end

步骤2以 fi在训练集上的精度构造权重，对生成的T个基分类器进行加权集成。

5 仿真实验

5.1 实验数据

实验采用KDD CUP 99（10%）数据集。从训练集随机抽取1000个样本（含攻击样本195个）组成训练集，如表1所示。从测试集随机抽取800个样本（含攻击100个）组成测试集。为检验本文算法对未知攻击的检测效果，加入训练集中没有的未知攻击10种，如表2所示。

表1 训练集攻击类型分布

表2 测试集攻击类型分布

5.2 算法评价标准

本文用检测率、误报率作为评价入侵检测系统性能的指标。

5.3 实验结果与分析

5.3.1 邻域粗糙集半径与入侵检测精度

首先使用邻域粗糙集对训练集s1进行属性约简，然后采用支持向量机在约简后的训练集上训练分类器，并在测试集s2上进行测试。实验重复20次，取其平均值作为实验结果。

邻域粗糙集模型是由实数空间中的每一个点形成一个δ邻域，而δ邻域则成为描述空间中任意概念的基本信息粒子。邻域的大小反映了人们对数值属性中噪声数据的容忍程度，所以邻域半径δ是影响邻域粗糙集模型性能的重要因素。不同的半径导致检测精度的差异，本文将邻域半径取在[0.01，0.5]，以0.01为步长，每取一个半径，则获得一个属性子集，共产生50个属性子集。

图2和图3分别直观地显示了入侵检测率、误警率与邻域半径之间的关系。从图2可以看出半径在[0.01，0.24]之间，其入侵检测率保持在80%左右，而当半径增加到[0.27，0.48]，检测率大幅提高，大概在91%左右，说明邻域半径对检测率的影响是比较显著的。从图3看到，半径在[0.01，0.48]之间，其误警率基本保持在2%左右，而0.48之后，误警率大幅增加。

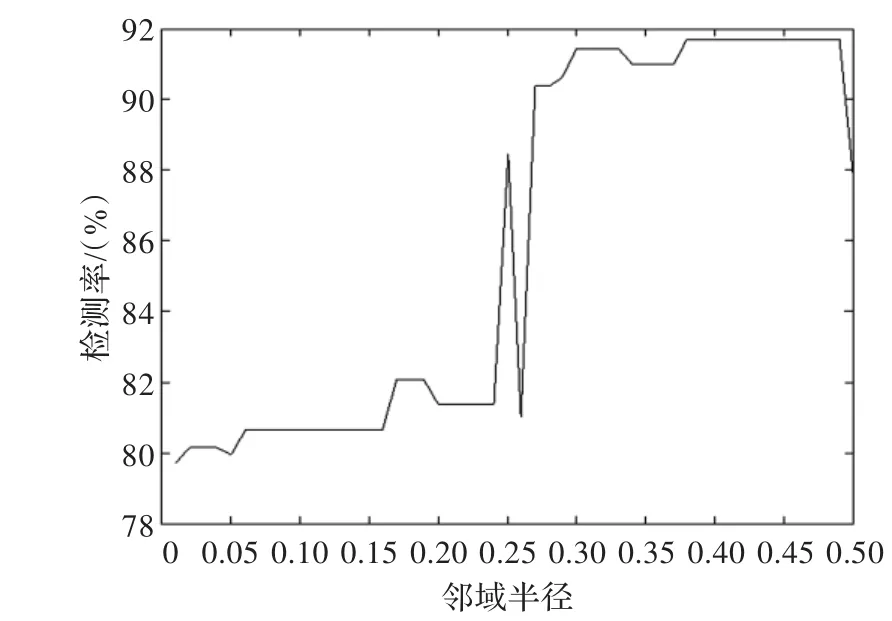
图2 邻域粗糙集半径与入侵检测率关系

图3 邻域粗糙集半径与入侵误警率关系

综上可得，当邻域半径在[0.35，0.48]之间，其检测率较高，同时误警率达到较低的状态，这说明较小的δ邻域使得粗糙集的边界区域较窄，正域较大，所以分类精度较高。当然，邻域的大小与所研究对象的内在特性有着密切关系，所以不能在任何情况下都取较小的δ。

5.3.2 算法的检测率与误警率

在训练集s1上采用本文方法进行SVM集成，并在测试集s2上验证算法的有效性和优越性。同样实验重复进行20次，取其平均值作为实验结果。

表3给出了利用本文算法所得到的入侵检测率及误警率结果。其中“平均”表示参加集成的多个基分类器检测率（或误警率）的平均结果；“最优”表示参加集成的多个基分类器中检测率最高（或误警率最小）的结果；“集成”表示利用本文算法所得到的集成结果。

从表3中可以看出，采用本文算法所得到的检测率（即“集成”）总体要比基分类器的平均检测率提高5%左右，而且集成值与基分类器的最优值相近，甚至超过最优值，说明集成算法的有效性。本文算法获得的误警率整体上降低了3%左右，而且集成值大部分都超过了基分类器的最优值，说明本文算法对于降低误警率有着显著的效果。另外，随着基分类器个数的增加，其检测率和误警率基本相似，所以可以减少基分类器的个数来进一步提高算法的时间、空间效率以及降低算法的复杂度。

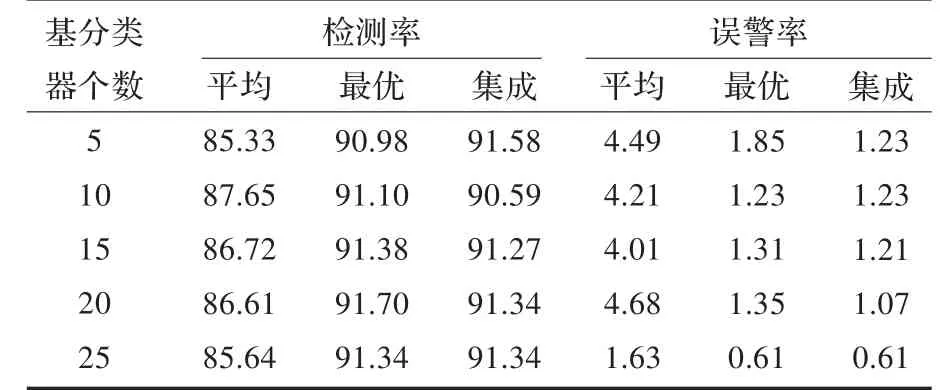
表3 本文算法的实验结果 （%）

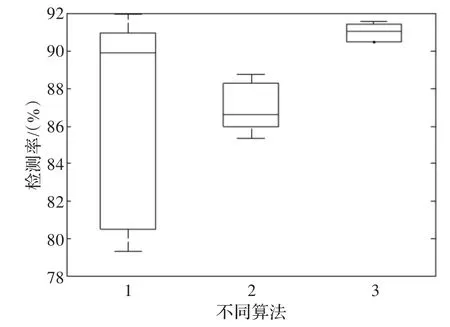
图4 不同算法检测率箱线图

图4显示了不同算法的稳定性。横坐标“1”表示各基分类器的入侵检测率，“2”表示各基分类器的入侵检测率的平均值，“3”表示各基分类器的集成检测率。

从图4看到，“3”（即“集成”）的稳定性最好，而且其检测率高于“2”（即“平均”）。说明本文算法在稳定性以及精确率两方面都超过其他算法。

表4给出算法1（SVM）、算法2（邻域粗糙集+SVM）和本文算法在已知、未知攻击上的检测率。本文算法相对于其他算法，对已知攻击数据的检测率平均提高约8%，而对于未知攻击数据的检测率平均提高约13%，说明该算法不仅对已知攻击检测有效，而且对未知攻击的检测依然有较好的效果，充分说明该算法具有较强的泛化性能。

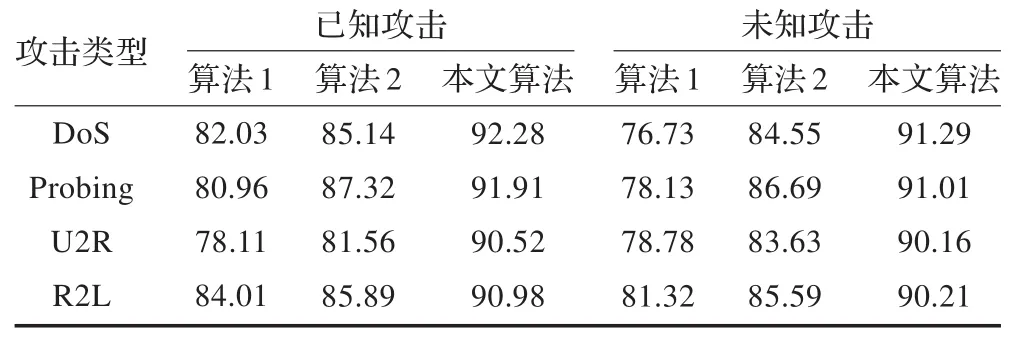
表4 不同算法对已知、未知攻击的检测率 （%）

6 结束语

入侵检测数据往往具有噪声和冗余属性，并且部分属性数据具有连续型特点，为了克服连续属性离散化过程中带来的信息损失，本文采用邻域粗糙集模型进行属性约简，并结合Bagging技术设计集成算法，在KDD99数据集上的仿真实验结果表明本文算法可以进一步提高入侵检测率，并同时降低误警率，该算法具有较强的泛化性能和鲁棒性。

[1]陈光英，张千里，李星，等.基于SVM分类机的入侵检测系统[J].通信学报，2002，23（5）：51-56.

[2]饶鲜，董春曦，杨绍全，等.基于支持向量机的入侵检测系统[J].软件学报，2003，14（4）：798-803.

[3]廖建平，余文利，方建文.改进的增量式SVM在网络入侵检测中的应用[J].计算机工程与应用，2013，49（10）：100-104.

[4]雷向宇，周萍.支持向量分类机在入侵检测中的应用研究[J].计算机工程与应用，2013，49（11）：88-91.

[5]陈涛.基于双重扰动的支持向量机集成[J].计算机应用，2011，28（1）：46-49.

[6]陈涛.基于加速遗传算法的选择性支持向量机集成[J].计算机应用研究，2011，32（2）：57-61.

[7]常甜甜，赵玲玲，刘红卫，等.多模式扰动模型动态加权SVM集成研究[J].计算机工程与应用，2011，47（6）：196-198.

[8]徐冲，王汝传，任勋益，等.基于集成学习的入侵检测方法[J].计算机科学，2010，27（7）：217-224.

[9]张义荣，鲜明，肖顺平，等.一种基于粗糙集属性约简的支持向量异常入侵检测方法[J].计算机科学，2006，33（6）：64-68.

[10]赵曦滨，井然哲，顾明，等.基于粗糙集的自适应入侵检测算法[J].清华大学学报，2008，48（7）：1158-1168.

[11]刘其琛，施荣华，王国才，等.基于粗糙集与改进LSSVM的入侵检测算法研究[J].计算机工程与应用，2012，48（8）：48-52.

[12]陈涛.基于动态粗糙集约简的选择性支持向量机集成[J].计算机仿真，2012，43（2）：328-331.

[13]Meng Z Q，Shi Z Z.A fast approach to attribute reduction in incomplete decision systems with tolerance relation based rough sets[J].Informstion Sciences，2009，17（16）：2774-2793.

[14]胡清华，于达仁，谢宗霞，等.基于邻域粒化和粗糙逼近的数值属性约简[J].软件学报，2008，15（3）：121-125.

[15]胡清华，赵辉，于达仁，等.基于邻域粗糙集的符号与数值属性快速约简算法[J].模式识别与人工智能，2008，21（6）：89-95.

[16]Hu Q H，Yu D R，Liu J F，et al.Neighborhood rough set based heterogeneous feature subset selection[J].Information Sciences，2008，178（18）：3577-3594.

[17]赵晖.融合邻域粗糙集与粒子群优化的网络入侵检测[J].计算机工程与应用，2013，44（12）：328-331.

[18]赵晖.基于邻域粗糙集与KNN的网络入侵检测[J].河南科学，2013，31（9）：1404-1408.

[19]Breiman L.Bagging Predictors[J].Machine Learning，1996，24（2）：123-140.

[20]陈涛.选择性支持向量机集成算法[J].计算机工程与设计，2011，18（5）：259-263.

[21]陈涛.一种新的支持向量机混合集成算法[J].科学技术与工程，2012，21（12）：5312-5315.

[22]Kuncheva L I.Combining pattern Classifiers：Methods and Algorithms[M].USA：John Wiley&Sons.Inc，2004：33-34.