安全高效的大矩阵行列式计算云外包协议

任晓霞，黄宏宇

REN Xiaoxia1,HUANG Hongyu2

1.重庆医科大学附属第一医院 信息中心，重庆 400000

2.重庆大学 计算机学院，重庆 400044

1.Information Center,The First Affiliated Hospital of Chongqing Medical University,Chongqing 400000,China

2.College of Computer Science,Chongqing University,Chongqing 400044,China

1 引言

云计算已经成为当前IT产业界的热门研究领域并且吸引了大量学者的目光。云计算存在的经济意义是将大量的计算资源，存储资源，软件资源链接在一起，形成规模经济效应。一些计算能力薄弱或者计算资源不足的客户端都可以将自己的计算任务发送给云服务端或计算能力相对较强的计算节点进行计算，这种计算架构比客户自己购买和维护一个运算设备更能充分利用CPU的运算空闲，提高运算设备的利用率，从而降低设备的成本[1-2]。因此，云计算被认为是IT产业未来一个重要的产业增长点。

尽管云计算看上去是充满希望的发展领域，但是它的发展依赖于许多重要工程技术问题的有效解决，安全问题便是首当其冲需要考虑的。根据云计算安全联盟和IDC（互联网数据中心）的调查，超过50%的企业认为安全和隐私问题是他们尚未使用云计算服务的主要原因。因此，密码学和安全研究团体不约而同地将研究的目光和重心转向了云安全的研究。密码学的研究由此转向了同态加密[3]，见图1。

图1 密码学新的发展

由于目前提出的同态加密方案效率比较低，距离实际的应用层面还有很长的路要走。在解决实际工程和科学计算工程中，计算安全学家提出了许多新技术来实现在计算外包中支持对密文进行可控的、有意义的以及高效操作的加密算法。例如Atallah等人在文献[4]中通过使用多种有效的技术手段来伪装掩盖原问题来实现外包数据的私密性，实现了关于安全外包许多科学计算问题的研究；但文献中方法存在两个方面的缺陷：一是协议的效率没有被仔细讨论，二是返回的计算结果没有得到正确性的验证。最近，Wang等人[5-6]提出了一个安全外包线性规划运算的协议和一个安全外包求解线性方程组的协议，这两个协议效率相当高并且能够立即在现实中部署使用，他们所提出的架构有着很强的现实指导意义；Atallah等人在文[7-8]中提出了一个安全外包序列比较的协议和一个安全代数计算协议；但是，两个协议的共同缺陷是：都需要效率不高的同态加密算法或者不经意传送协议[11]，使得协议对大规模运算问题效率很低。

大矩阵行列式计算是一个很基础的科学计算问题，在工程和科学上有着大量的应用。例如，利用矩阵行列式值和Cramer法则可以实现对线性方程组的求解。此外，行列式计算在数学物理分析[9]，拉格朗日插值分析[10]等领域有着广泛的用途。

针对此类科学计算问题，本文构建了一个关于大矩阵行列式计算外包的协议，此协议可以使得计算能力薄弱的客户端将大矩阵求行列式值的计算外包给计算能力强大的云计算端服务器，并且实现正确性、安全性以及高效性的设计目标。

2 相关模型、设计目标以及外包协议的框架描述

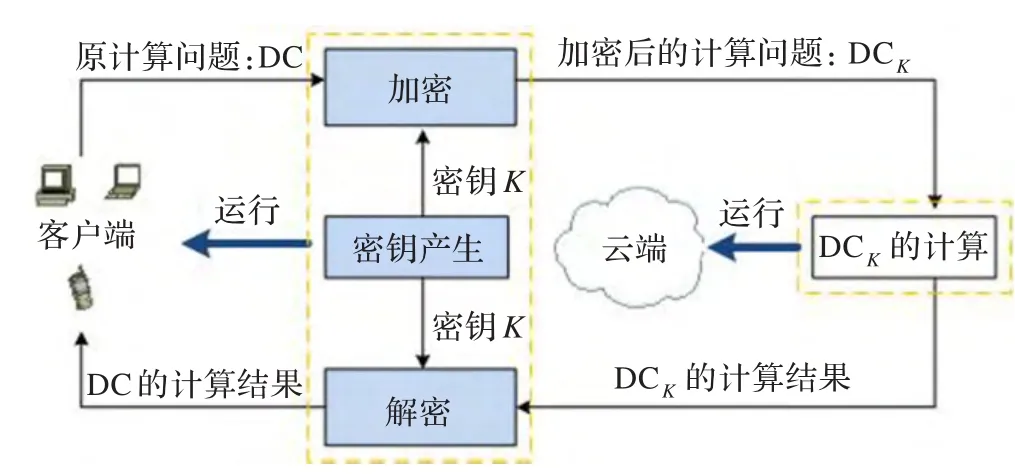
图2 安全行列式计算外包系统模型

系统模型：本文研究的整体系统模型如图2所示，其中Determinant Computation（DC）代表行列式计算。客户端在将计算外包之前，为了保护输入私密性，先利用密钥K将原始的计算问题DC，加密成一个新的计算问题DCK；随后，客户端将DCK传输给云服务端进行运算；云服务端接收到新的计算问题DCK计算出相应的运算结果；云服务端将DCK的结果传送给客户端，客户端利用密钥K解密从云服务端收到的结果，得到原始计算问题DC的结果。这样一个安全外包计算DC行列式值的流程就完成了。

威胁模型：本计算模型所面临的安全威胁主要来自于云服务端。本文假设云服务端是半诚实的（semi-honest）。完整定义如下：

定义1（半诚实模型[11]）云服务器总会忠实地执行协议，但是会记录所有信息，用以推导客户端的敏感信息。

这个安全模型考虑了如下两种安全威胁：（1）云服务器端会分析客户端发送的加密数据以及返回给客户端的运算结果来获取客户端的敏感信息；（2）云服务器端被第三方入侵而导致内部信息的泄露。针对这两种威胁，本文所设计的协议可以实现在一个半诚实的云服务器下安全运行。

设计目标：本协议需要现实如下三个目标：

（1）正确性

如果客户端和云服务端都按照协议运行，则云服务端能够返回给客户端一个正确的计算结果。

（2）输入/输出私密性

①输入私密性：云服务器不能从加密后的DCK获得原始的计算问题DC；②输出私密性：云服务器不能从DCK的计算结果中得到DC问题的运算结果。

（3）高效性

①客户端本地的总运算量要明显少于自己运行DC的运算量；②云服务端计算DCK的运算量要和计算原问题DC的运算量尽量地保持一样。

协议架构：根据本文提出的系统模型可以得出，一个安全外包DC的协议应包含四个子算法：（1）密钥产生算法KeyGen；（2）客户端 DC加密算法DCEnc；（3）云服务器端运算DCK的算法DCSolve；（4）客户端解密算法DCDec。一旦明确了协议的基本架构，下面只需要在协议构建中将各个子算法一一实现即可。

3 协议构建

置换函数在群论[12]和组合论[13]中被广泛地研究，利用柯西的两行表示法，一个置换函数可以表示成：

本文利用一个置换函数 π(i)=pi，i=1，2，…，n表示式（1）。同时，利用sign(π)来表示置换函数π的奇偶性：如果π是偶置换函数则sign(π)=-1；如果π是奇置换函数则sign(π)=1。置换函数的奇偶性的详细定义，参见文献[12]。克罗内克函数定义为：

对于一个矩阵 X∈ℝn×n，使用 X(i，j)，xi，j，或者是xij来表示矩阵X中第i行第 j列的元素，det(X)表示矩阵X的行列式值。

考虑一个非奇异的矩阵 X∈ℝn×n，客户端想要将计算det(X)外包给一个半诚实的云服务器端。协议的每个子算法依次构建如下。

（1）密钥产生算法KeyGen：输入一个安全参数λ，客户端调用算法1来生成密钥K：π，{α1，α2，…，αn}。

算法1生成密钥

输入：一个安全参数λ。

输出：密钥 K ：π，{α1，α2，…，αn}。

第一步：安全参数λ规定密钥空间Kα。客户端选择 n个随机数{α1，α2，…，αn}←Kα，这里 0∉Kα。

第二步：客户端调用算法2来产生一个1，2，…，n的随机置换函数π。

算法2生成随机函数

第一步：设置π=In，这里In表示恒等置换

第二步：fori=n:2

第三步：设置 j在1≤j≤i中的随机数

第四步：交换π[j]和π[i]

第五步：end for

（2）客户端DC的加密算法DCEnc(X，K)：输入一个原始矩阵X和密钥K，客户端调用算法3来加密原来的矩阵X得到加密后矩阵Y。

算法3 DC加密

输入：原始矩阵 X 和密钥 K:π，{α1，α2，…，αn}。

输出：Y=PX。

第二步：客户端计算Y=PX。根据定理2，客户端可以快速地利用公式（4）来计算Y（使用时间复杂度O(n2)）。

第三步：随后，加密的矩阵Y将被传送给云服务器端进行相关计算。

证明 由于 P(i，j)= αiδπ(i)，j，不难得出：矩阵 P 总可以通过基本行列式变换为一个新的矩阵P′，使得P′所有对角线元素为 {α1，α2，…，αn}，而其他位置元素全为0。交换的次数的奇偶性由置换函数π决定。由引理1可得到交换次数为偶数时有 ；交换次数为奇数时有 。综上所述容易得到，证毕。

定理2 在算法3中，P(i，j)= αiδπ(i)，j，则矩阵 Y 满足

证明 矩阵X被表示为：

因为Y=αiX(π(i)，j)，可以得到：

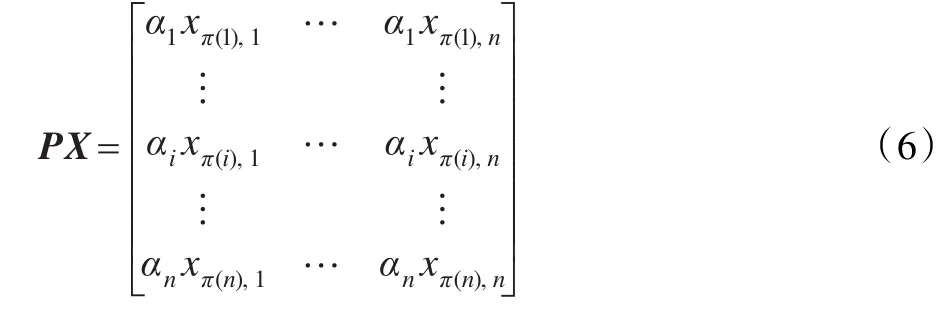
公式（6）可以进一步简写为

Y(i，j)=PX= αiX(π(i)，j)

（3）云服务器端运算DCK的算法DCSolve(Y)：输入一个加密后的矩阵Y，云服务端调用算法4得到矩阵Y的行列式值DY。

算法4DCK计算

输入：Y。

输出：DY。

第一步：从客户端接收到密钥后的矩阵Y，云服务器端调用任何存在的算法计算Y的行列式值DY，即DY=det(Y)。

第二步：云服务器返回DY给客户端。

（4）客户端解密算法DCDec(DY，K)：输入返回的运算结果DY和密钥K，客户端调用算法5便得到原始矩阵X的行列式值DX。

算法5 DC解密

输入：密钥 K:π，{α1，α2，…，αn}和 DY。

输出：DX。

第一步：根据密钥 π，{α1，α2，…，αn} ，客户端计算。

第二步：从云服务器端接收到DY。客户端计算DX=DY/DP。客户端便得到原始矩阵X的行列式值DX。

根据第一章中的系统模型要求，一个完整的协议已经构建完成，下面需要分析本协议是否可以达到正确性、输入/输出私密性和高效性的目标。

4 协议分析

4.1 正确性分析

定理3本文的协议满足正确性。

证明 在此只需要证明如果客户端和云服务器端都诚实地执行了本文的协议，则DX总是原始矩阵X的行列式值。因为Y=PX，所以det(Y)=det(P)det(X)，即DY=det(P)DX。进一步由公式（3），便得到DX=DY/DP，这就保证了在DC解密运算中DX总是原始矩阵X的行列式值。

4.2 输入/输出私密性分析

输入私密性：客户端数据在半诚实的云服务器端所面临的威胁之一是，云端试图从加密后的矩阵Y还原出原始的矩阵X。原始的矩阵通过以下2个步骤进行了加密。

步骤1原始矩阵X的每行的元素被随机的置换，即 T(i，j)=X(π(i)，j)。

步骤2被置换后的矩阵进一步通过乘一个因子来加密，即Y(i，j)=αiT(i，j)。

在步骤1中由于π是随机产生的置换函数，所以有一共n!种情况，云端即使得到了矩阵T，利用蛮力搜索法从矩阵T中得到正确的X期望时间是n!/2。当n足够大的时候此方法不可行。在步骤2中T被进一步通过乘以一个因子来加密，如果密钥空间Kα足够大，则从Y中还原出T攻击是很困难的。进一步考虑到协议中对于每一个外包的DC实例，密钥都会重新产生一次，如果云服务器端没有密钥K，从加密后的矩阵Y还原出原始的矩阵X是非常困难的。因此，输入私密性得到保证。

输出私密性：客户端数据在半诚实的云服务器端所面临的另外一个威胁是，云端试图从运算结果DY中去还原出DX。由于DX=DY/DP，由公式（3），，如果选取适当的密码空间 Kα，可以使得DP的取值范围非常大。在这种情况下，考虑每次加密DP的取值会变化，DY中去还原出DX也是困难的。因此，输出私密性得到保证。

5 效率评估

5.1 理论分析

客户端的计算量包含：密钥产生，DC的加密，DCK的解密算法三部分，分别对应于KeyGen，DCEnc和DCDec算法；而云服务器端的计算量仅由运行DCSolve产生。实验假设云服务器端采用了最为常见的矩阵LU分解法[14]来计算行列式值，则DCSolve运行的时间复杂度为O(n3)。表1总结了各个算法理论上的时间复杂度。由表1可知，客户端总的时间复杂度为O(n2)，而云服务器端为O(n3)。根据计算复杂性中的大O符号的定义[15]，可以得到当问题规模n足够大的时候，客户端的运算量会远远小于云服务器端的运算量。

表1 协议的理论开销

5.2 实验结果

理论分析已经证明，协议能够节省客户端的运算量。本节通过实验来评估协议的实际效率。实验中将客户端和云服务器端部署在同一个工作站上来测量它们的运行时间，这样客户端和云服务器端的计算量可以通过时间的比例来客观地反应（参见下一段客户端加速比的定义），如果将客户端和云服务器端部署在两个不同的服务器上，则客户端加速比将变得不稳定，取决于两个服务器的运算速度的差距。因此，实验采用一个服务器的实验模式。实验中，客户端和云服务器计算都是在同一个工作站上执行，这个工作站的配置为：英特尔（R）赛扬1.8 GHz的CPU，1 GB RAM。实验将忽略掉客户端和云服务器端的通信延迟，因为本实验中计算时间占整个运行时间的主要部分。

实验的目的是计算外包后客户端的性能增益。本协议可行的前提条件是以下公式满足：

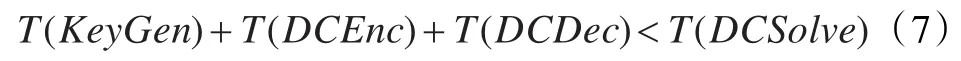
换而言之，客户端在运行密钥生成，DC加密，以及DC解密所花费的总时间要比自己去解决原始的DC计算问题本身所耗费的时间要少。根据表2中参数的定义，不等式（7）所阐述的意义，可以用toriginal/tclient来测定，即本地计算时间和外包计算时间的比值。此比值定义为客户端的加速比，这个值理论上应该为一个大于1的正数，表示本协议获得了一个很可观的性能增益。除此之外，在实验中，云端效率是需要考虑的另外一个指标，公式表示为toriginal/tcloud。此指标反映处理加密后的计算问题和处理原始问题时间的比值。理想情况下，处理DCK不能增加解决原始DC的时间，理想的云端效率值应接近1。

表2 协议实验参数

实验由Matlab实现，云服务器端使用的是Matlab所提供的函数来计算矩阵的行列式值。本质上是通过Matlab所提供的接口调用线性代数包LAPACK[16]中的函数。所有的矩阵是随机产生保证其是非奇异的。实验中使用 Kα={1，2，…，n}。实验的数据由表3所示。从中可以看出，客户端的加速比随着问题的规模单调递增。客户端在n=2500时，能够获得约10倍的客户端加速比。客户端加速比和矩阵规模n的关系如图3所示。图4表示了云端效率和矩阵规模n的关系，可以看出云端的效率始终保持在1左右。结果表明加密矩阵没有使得对应的行列式计算复杂度变得更高。这是一个非常理想的结果。

表3 DC外包的实验数据

图3 客户端加速比和矩阵维数的关系

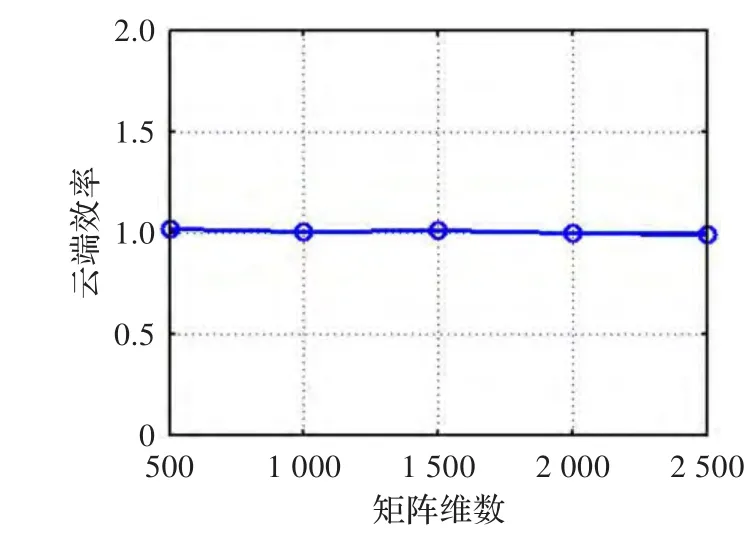
图4 云端效率和矩阵维数的关系

由实验得出：当问题规模足够大时，本文协议是非常高效的。

6 总结

本文设计了一个实现了安全性和高效性的行列式计算的云外包协议。理论和实验分析显示，此协议同时满足正确性，输入/输出私密性以及高效性。由于行列式的计算是一个在工程以及科学计算上广泛应用的基本运算，故该协议可被广泛使用；另外也可以利用此协议为基础构建设计更高层的计算外包协议，或者为其他的工程和科学计算问题设计安全的云外包协议。

[1]Wang Cong，Ren Kui，Wang Jia.Secure and practical outsourcing of linear programming in cloud computing[J].IEEE Transactions on Cloud Computing，2011，4：10-15.

[2]罗军舟，金嘉晖，宋爱波，等.云计算：体系结构与关键技术[J].通信学报，2011，32（7）：4-21.

[3]Gentry C.A fully homomorphic encryption scheme[D].Proquest，Umi Dissertation Publishing，2011.

[4]Atallah M，Pantazopoulos K，Rice J，et al.Secure outsourcing of scientif i c computations[J].Advances in Computers，2002，54：215-272.

[5]Wang C，Ren K，Wang J.Secure and practical outsourcing of linear programming in cloud computing[C]//INFOCOM，2011 Proceedings.[S.l.]：IEEE，2011，4：820-828.

[6]Wang C，Ren K，Wang J，et al.Harnessing the cloud for securely solving large-scale systems of linear equations[C]//31st International Conference on Distributed Computing Systems（ICDCS）.[S.l.]：IEEE，2011，11：549-558.

[7]Atallah M，Li J.Secure outsourcing of sequence comparsion[J].Int J Inf Secur，2005，4：227-287.

[8]Benjamin D，Atallah M J.Private and cheating-free outsourcing of algebraic computations[C]//Proc of 6th Conf on Privacy，Security，and Trust（PST），2008，12：240-245.

[9]Vein R，Dale P.Determinants and their applications in mathematical physics[M].New York：Spriger-Verlag，1999.

[10]Chui C K，Lai M J.Vandermonde determinant and lagrange interpolation in rs[J].Nonlinear and Convex Analysis，1987，107：23-35.

[11]肖倩，罗守山，陈萍，等.半诚实模型下安全多方排序问题的研究[J].电子学报，2008（4）：709-714.

[12]赫尔.群论[M].北京：科学出版社，1981.

[13]布鲁迪.组合数学[M].北京：机械工业出版社，2012.

[14]王开荣，杨大地.应用数值分析[M].北京：高等教育出版社，2010.

[15]戈德赖希.计算复杂性[M].北京：人民邮电出版社，2010.

[16]巴克.LAPACK95 users’guide[M].北京：清华大学出版社，2011.