考虑类内不平衡的谱聚类过抽样方法

骆自超，金 隼，邱雪峰

LUO Zichao,JIN Sun,QIU Xuefeng

上海交通大学 机械与动力工程学院，上海 200000

School of Mechanical Engineering,Shanghai Jiaotong University,Shanghai 200000,China

1 引言

不平衡数据集指某些类包含的样本数远大于其他类样本数的数据集。在分类算法的现实应用中，不平衡的数据结构是一个普遍存在的问题，例如识别油井泄漏[1]、进行医学诊断[2]、检测信用卡诈骗[3]等等。研究者发现不平衡数据结构会降低分类算法的性能。

不平衡分类中，样本数较少的类叫做少数类，这类样本往往是关注的重点，需要很高的识别精度。但是标准分类器是基于数据平衡分布的假设建立的，在处理不平衡数据集中，难以得到令人满意的少数类识别率。为此，不平衡数据分类问题越来越受到学界广泛关注，并且被一些学者认为是数据挖掘领域的关键挑战之一[4]。

不平衡数据集中少数类样本往往可以再划分为几个子类，因此数据的不平衡结构可再细分为类间不平衡与类内不平衡。前者指多数集与少数集之间存在的数据样本量不平衡情况，后者则是少数类样本中各子类间样本数据量的不平衡。

当前解决不平衡分类问题的方法可以分为算法层面的方法和数据层面的方法两类：前者是通过改进标准分类算法，使分类器适应不平衡数据集下的分类；后者则是通过对数据集进行处理，减少数据不平衡程度，从而使分类器能够在平衡的数据集上进行学习，提高少数类的分类正确率。

数据层面的不平衡分类处理方法又分为欠抽样和过抽样，在过抽样方法中，基于聚类的过抽样方法[5-9]是较受学者关注的一类。当前基于聚类的过抽样方法有两方面不足：首先，这类方法主要建立在k均值聚类算法的基础上，聚类效果对初始中心的选择和分类个数的选定非常敏感，并且倾向于生成大小相似的类，在实际应用中聚类不稳定、效果有待提高；其次，这类方法仅考虑类间不平衡，没有考虑普遍存在的类间不平衡的情况。

针对以上两个问题，本文提出一种基于改进的谱聚类的过抽样方法处理存在类内不平衡的数据集。该方法首先自动选择合理的聚类个数并对少数类样本进行谱聚类，再根据簇内包含的样本个数与少数类总样本数之比决定对每个簇生成的新样本数量，最后采用SMOTE方法进行新样本生成，使数据集在类间和类内均趋于平衡。

2 不平衡数据集处理方法

不平衡数据分类问题处理方法分为算法层面和数据层面两类。Maloof等指出，通过算法层面方法调整误分代价策略获得的分类面和在经过数据重抽样的数据集上进行学习获得的分类面几乎完全一致[10]。即采用这两类方法获得的结果是非常相近的，因此本文只研究数据层面的不平衡数据集处理方法。

另外，本文的研究只针对二分类问题，即一个数据集中仅含有一个多数类和一个少数类。对于多分类的情况，可以将其分解为多个二分类问题[11]，或者通过逐对耦合方法，将针对二分类的算法扩展到多分类问题[12]。

针对二分类的不平衡数据分类问题，数据层面的方法分为欠抽样和过抽样两类，前者减少多数类中包含的样本数，从而获得相对平衡的新数据集，后者则在少数类中生成新的样本点，使新数据集达到平衡。

2.1 欠抽样方法

最原始的欠抽样方法是随机欠抽样，这种方法从多数类中随机删去数据样本，从而获得平衡数据集。这类方法的主要缺陷在于可能删去数据集中的重要信息。Kubat[13]提出了单侧选择（One-Sided Selection）算法，检测并删除多数类中的冗余和噪声点，从而获得较为清晰的边界。Yen和Lee[14]提出了基于聚类的欠抽样方法，首先对所有训练样本进行聚类，再根据多数类样本数与少数类样本数之比计算每个类中应该保留的样本个数，最后随机删除每个类中的多数类样本，使得该类中样本总数满足要求。Yu等[15]提出ACOsampling，用蚁群算法寻找原始多数类集中最优的子集，从而筛选出多数类中包含最多信息的样本点。将该子集与原少数类重新组合，即获得相对平衡的新数据集。

2.2 过抽样方法

过抽样方法中，随机过抽样方法随机复制少数类样本，而不对多数类数据进行处理。该方法会导致分类器，尤其是分类树的决策域收缩，从而引起过拟合[16]。由 Chawla等[17]提出的 SMOTE（Synthetic Minority Oversampling Technique）算法在特征空间中相邻的样本之间进行线性插值，从而获得需要的新少数类样本。Han等[18]发现不平衡数据分类中，误分样本大多位于多数类和少数类的边界上，因此他们提出先筛选出位于边界上的少数类样本。在进行过抽样时，只对边界上的少数类样本进行操作。He等[19]针对之前的过抽样方法没有考虑到样本分布，对每个样本合成同样数量的新数据样本的问题，以每个少数类样本k个最近邻样本中多数类样本的数量为依据，为周边多数类样本多的少数类样本生成较多新样本。为了防止在过抽样中生成噪声，Barua等[6]设计了CBOS（Cluster Based Synthetic Oversampling）算法，利用层级聚类先对少数类进行聚类，再在每个类之内合成新样本。

3 基于改进谱聚类的过抽样方法

本文提出一种基于改进谱聚类的过抽样方法（Spectral Clustering based Over Sampling，SCOS），该方法首先自动确定聚类个数，再对少数类数据集进行谱聚类，之后根据每个类内包含的样本个数与总的少数类样本个数之比，确定在每个类内部合成的样本数，最后通过在类内部进行SMOTE过抽样，获得相对平衡的新数据集。算法流程框图如图1所示。

图1 算法流程图

3.1 改进的谱聚类算法

谱聚类（Spectral Clustering）算法的思想来自图论，它将每个数据作为一个图节点，将聚类问题转化为带权无向图的分割问题[20]。尽管构建的相似度表征和映射方法不同，导致具体实现方法很多，但是谱聚类的基本思路都是先对样本数据的相似矩阵进行分解，再将得到的特征向量进行聚类[21]。

标准谱聚类中，聚类数需要根据经验选择，但是面对未知的数据结构，聚类数的人工选择往往会造成某些类中数据量过少，这对于过抽样中新样本的生成是非常不利的。针对这个问题，本文改进谱聚类方法使其自动选择聚类数，以保证每个类中样本数都达到一定值，以便下一步进行过抽样。具体实现步骤如下：

（1）将初始聚类数k设为10。

（2）取出少数类样本，设少数类集中包含n个样本，则可用一个n×n矩阵W表述少数类数据样本两两之间的相似性：

W(i，j)代表数据点Si与Sj之间的相似程度，且有W(i，j)=W(j， i)， W(i，i)=0 。其中，d(si，sj)取为欧几里德距离，σ为尺度参数。

（3）根据下式计算矩阵D：

（4）令L=D-W ，根据聚类个数k求L矩阵的前k个特征值（按照特征值升序排列）以及对应的特征向量。

（5）将这k个特征向量按列排成一个n×k矩阵，其中每一行可以看作原数据点在k维空间中的投影坐标。用k均值聚类算法对这n个少数类样本点进行聚类。

（6）检验是否每个类中样本数均大于n/20，如果满足该条件，则聚类结束；如果不满足，则k=k-1，重复步骤（2）～（5）。

3.2 优化的SMOTE算法

SMOTE算法因为其易于实现以及在现实应用中效果显著，被学者大量应用于解决不平衡分类问题，但是SMOTE算法对每个少数类样本均生成相同个数的新样本，对类内不平衡没有改善作用。为解决这个问题，本文优化了SMOTE算法，在合成新样本之前，根据每个类内包含的样本个数与总的少数类样本个数之比，确定在每个类内部合成的样本数，以平衡少数类的子类数据量。具体步骤如下：

（1）根据过抽样比率η，计算需要生成的少数类样本个数：

其中，n为少数类样本总数。

（2）计算每个类包含样本个数与少数类总样本个数之比：

其中Ci为每个类所包含样本个数。

（3）将 g从大到小排序，记录 gi对应的序号 j，j=1，2，…，k。

（4）计算为每个类合成的样本数：

（5）在每个类内执行SMOTE算法（步骤参见文献[16]），生成指定个数的样本。

4 实验设定

为验证上述算法的有效性，本文在一个合成数据集和四个来自UCI机器学习数据库的实际数据集上，将本文提出的算法与SMOTE[17]、CBOS[6]和基于k均值聚类的过抽样算法[8]进行对比测试。在获得相对平衡的数据集后，用标准CART（Classification And Regression Tree）分类树[22]进行分类，测试中采用三次独立的十折交叉验证（10-fold cross validation），最终性能度量取三次的平均值。

4.1 数据集

（1）为验证本文算法在实际不平衡数据集分类中的性能，本文在表1所列出的四个实际数据集上对算法进行测试。在具有多个类别的数据集中，选取其中一类为少数类，而将其他所有类别合并成为多数类。

表1 数据集描述

（2）为进一步考察基于k均值和谱聚类的两种过抽样方法在目标数据集存在少数类类内不平衡，区域重合（绿色与红色区域部分重叠）和类间距离差异等特性下的性能，采用如图2所示二维合成不平衡数据集对进行测试。图2（a）中，黑色点代表10000个多数类样本，青色代表少数类样本，共1600个。少数类本身存在类内不平衡，它由图2（b）所示绿色区域的1000个样本，红色区域的500个样本和蓝色区域的100个样本组成。其中该绿色区域中心为[0.4，0.5]，红色区域为[0.7，0.3]，蓝色区域为[0.8，0.8]。

4.2 评价指标

在不平衡分类问题中，少数类具有更高的价值，误分少数类和误分多数类的代价不同，传统分类中广泛采用的总体精度基于两类误分等代价的假设，无法准确体现分类器性能。在不平衡分类中，F-measure和G-mean是更加合理的评价指标，在许多研究中得到应用。它们的计算方式如下：

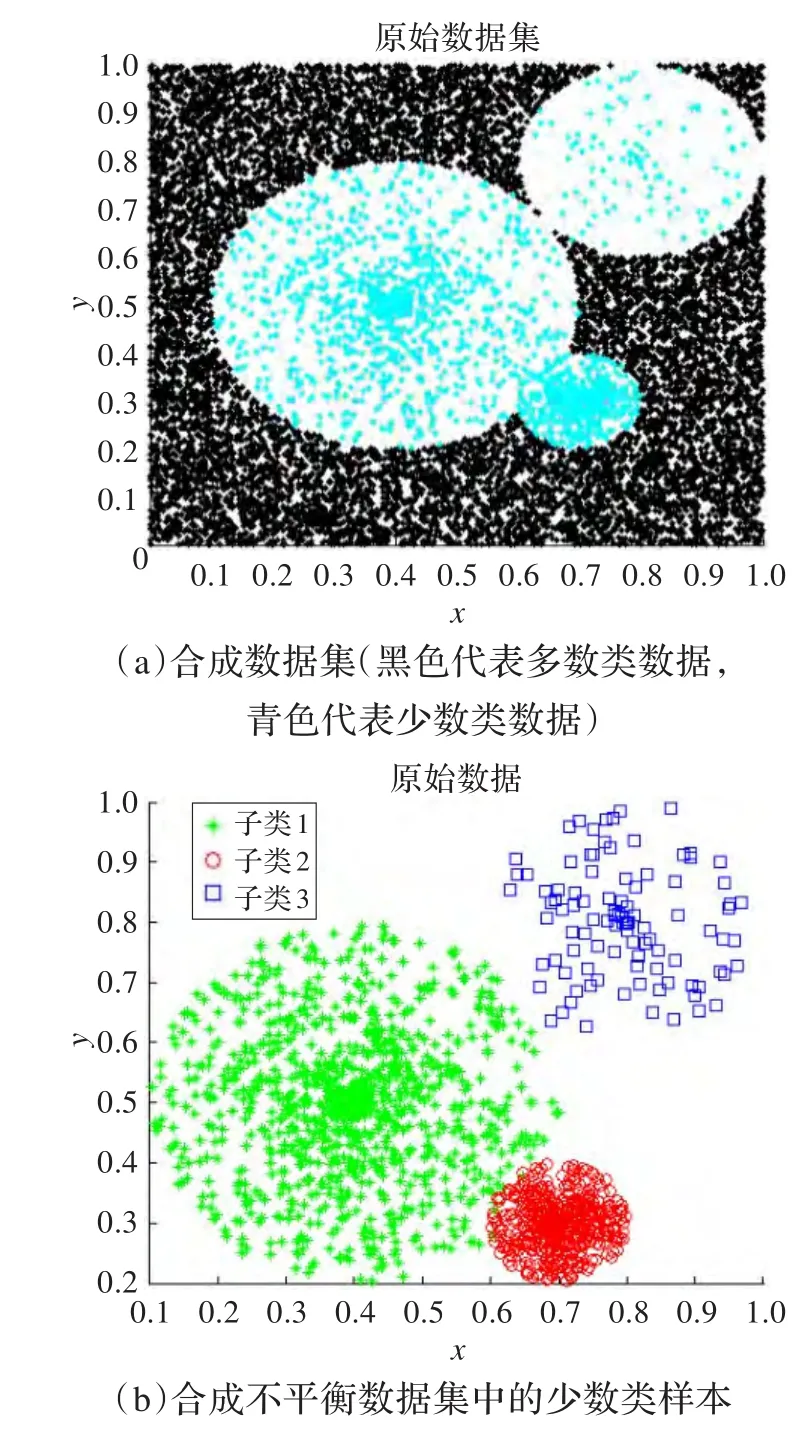
图2 合成数据集的数据结构

其中 β表示Precision和Recall的相对重要性，通常设为1。 F-measure和G-mean都是0到1之间的值，值越大，分类器性能越好。上式中Precision，Recall，Acc+和Acc-的定义如下：

其中，Tp，Fp，Tn，Fn分别表示被分类器正确分类的少数类样本个数，被错误分类的少数类样本个数，被正确分类的多数类样本个数，被错误分类的多数类样本个数。

为全面评价算法性能，本文同时采用F-measure，G-mean和Recall三个评价指标对分类结果进行评估。

5 实验结果与分析

5.1 实际数据验证结果

在实际数据集上进行验证时，算法参数的选择如下：过抽样比率设为200%，谱聚类的尺度参数σ设为0.02，SMOTE中近邻数设为5，基于k均值聚类的过抽样算法中，为更好对比聚类部分对整个算法性能的影响，其聚类数也采用3.1节中描述的自动选择方法确定。在原始数据（Origin）以及经过SMOTE算法、CBOS算法、基于k均值聚类的过抽样算法和本文提出的SCOS算法四种不同过抽样方法处理过的数据集上用CART进行分类，结果如表2所示（评价指标中最好的用粗体表示）。

表2 过抽样率200%时不同方法实验结果对比

本文选取了不同不平衡率、不同维数的四个不平衡数据集对算法进行了测试，实验结果表明：

（1）对比原数据集，在过抽样方法处理过的数据集上使用分类器能显著提高分类结果。

（2）对比SMOTE和其他三种方法，可以观察到基于聚类的过抽样方法对不平衡分类效果的提升作用更加明显。这是因为SMOTE算法的假设较为简单，没有考虑少数类在样本空间中分布的情况，因此在新样本合成中会引入噪声，影响最终的分类精度。

（3）本文提出的研究方法在四个数据集上都取得了很好的效果，证明了基于谱聚类的过抽样方法的有效性。

5.2 合成数据测试结果

由于算法复杂度低、实现容易等优点，k均值聚类在基于聚类的过抽样方法中被学者大量采用[8-9，23]。但是k均值聚类对聚类个数设定敏感，鲁棒性差，并且倾向于将数据集划分为大小相同的类。这些特点让基于k均值聚类的过抽样方法在处理存在类内不平衡的数据集时，可能在多数类所处区域合成大量噪声，反而降低分类器的总体性能。

为了排除实际数据集中难以避免的对分类器性能造成影响的其他因素，本文采用合成数据集仅仅针对类内不平衡验证不同聚类方式对过抽样算法的影响。本文在过抽样率分别为100%，200%，300%，400%，500%，600%的条件下，在合成数据集上对基于k均值聚类的过抽样方法和基于谱聚类的过抽样方法性能进行研究。结果如表3所示。

为更直观比较二者性能，将表3结果可视化如图3所示。

图3 两种基于聚类的过抽样方法性能图

通过对比图3（a）与图3（b）可以观察到，基于不同聚类方法的过抽样算法在性能表现上有一定差异：基于k均值聚类的过抽样方法对少数类样本的分类精度在达到一定高度之后基本保持稳定，但是F-measure和G-mean在过抽样率300%到600%时呈下降趋势，这说明随着新样本的生产，基于k均值聚类的过抽样方法在少数类中生成了一些噪声点，导致部分多数类样本被错误地划分入少数类，从而引起分类器综合性能下降。而基于谱聚类的过抽样方法随着过抽样率的增加，总体上保持性能上升，说明这种方法能有效减少噪声生成。

为了研究上述两种基于聚类的过抽样方法性能差异的原因，对图2（b）表示的少数类样本分别进行k=3，k=4，k=5的k均值聚类和谱聚类（谱聚类中σ取0.02），结果如图4和图5所示。

对比图4和图5，可以观察到k均值聚类在预先给定的聚类数不合理时(k=4，5)，倾向于将样本数多的子类进行分割，不能忠实反映原数据集的特性；即使给定了正确聚类数(k=3)，k均值算法仍然倾向于获得大小相近的类，因此出现了图4（a）中，两个包含样本数目较少的类（红、蓝区域）对样本数较多的类（绿色区域）的“入侵”。而在图5中，可以明显看到谱聚类的结果更加稳定，在给定类数据不合理时，仍然能很好地反映原始数据的结构。

聚类的结果很好地解释了随着过抽样率提高，两种方法在性能表现上的差异：在图4所示的k聚类基础上进行过抽样，则在蓝色所示类中合成新样本，会出现落在多数类区域的噪声点，影响分类器的综合性能。而基于谱聚类进行过抽样时，这个问题得到了很大改善。因此随着过抽样率的提高，基于k均值聚类的过抽样算法性能下降，而基于谱聚类的过抽样算法性能保持稳定。

表3 过抽样率改变时两种过抽样方法实验结果对比

图4 不同k值情况下k均值聚类结果

图5 不同k值情况下谱聚类结果

6 结论

不平衡数据分类问题是数据挖掘领域面临的重要挑战之一，过抽样方法是解决不平衡问题的一种有效方法。

在之前过抽样算法中，学者们对类内不平衡问题缺乏重视。本文提出了一种基于改进谱聚类的过抽样方法，该方法首先自动确定聚类数，再对少数类数据集进行谱聚类，之后根据每个类内包含的样本个数与总的少数类样本个数之比，确定在每个类内部合成的样本数，最后通过在类内进行SMOTE过抽样，获得相对平衡的新数据集。

通过在现实数据集上的测试，本文提出方法的有效性得到了验证。本文进一步研究了在二维合成数据集上基于k均值聚类和谱聚类过抽样方法的性能，发现聚类效果对过抽样算法的最终性能有重要影响。谱聚类算法的鲁棒性强，对聚类数选择不敏感，基于该方法进行过抽样能获得较好的效果。

[1]Kubat M，Holte R C，Matwin S.Machine learning for the detection of oil spills in satellite radar images[J].Machine Learning，1998，30（2/3）：195-215.

[2]Ling C X，Sheng V S，Yang Q.Teststrategiesfor cost-sensitive decision trees[J].IEEE Transactions on Knowledge and Data Engineering，2006，18（8）：1055-1067.

[3]Chan P K，Stolfo S J.Toward scalablelearning with non-uniform class and cost distributions：a case study in credit card fraud detection[C]//Proceedings of the 4th International Conference on Knowledge Discovery and Data Mining，New York，1998：164-168.

[4]Yang Q，Wu X.10 challenging problems in data mining research[J].International Journal of Information Technology&Decision Making，2006，5（4）：597-604.

[5]陈思，郭躬德，陈黎飞.基于聚类融合的不平衡数据分类方法[J].模式识别与人工智能，2010，23（5）.

[6]Barua S，Islam M M，Murase K.A novel synthetic minority oversampling technique for imbalanced data set learning[C]//Proceedings ofthe 18th InternationalConference on Neural Information Processing，2011，7063：735-744.

[7]Kollios G，Gunopulos D，Koudas N，et al.Efficient biased sampling for approximate clustering and outlier detection in large data sets[J].IEEE Transactions on Knowledge and Data Engineering，2003，15（5）：1170-1187.

[8]陈川，张化祥.基于聚类的少数类样本采样方法[J].信息技术与信息化，2011（5）：65-68.

[9]杨永，王莉利.基于K-means聚类和遗传算法的少数类样本采样方法研究[J].科学技术与工程，2010，10（10）：2334-2338.

[10]Maloof M A.Learning when data sets are imbalanced and when costs are unequal and unknown[C]//Proceedings of International Conference on Machine Learning，Workshop on Learning from Imbalanced Data Sets II，Washington DC，2003.

[11]Ou G，Murphey Y L.Multi-class pattern classification using neural networks[J].Pattern Recognition，2007，40（1）：4-18.

[12]Fernández A，Del Jesus M J，Herrera F.Computational intelligence forknowledge-based systems design[M].Heidelberg：Springer，2010：89-98.

[13]Kubat M，MatwinS.Addressingthecurseofimbalanced training sets：one-sided selection[C]//Proceedings of the 14th International Conference on Machine Learning，San Francisco，1997，97：179-186.

[14]Yen S J，Lee Y S.Cluster-based under-sampling approaches for imbalanced data distributions[J].Expert Systems with Applications，2009，36（3）：5718-5727.

[15]Yu H，Ni J，Zhao J.ACOSampling：an ant colony optimization-based undersampling method forclassifying imbalanced DNA microarray data[J].Neurocomputing，2012，101：309-318.

[16]Weiss G M，Provost F J.Learning when training data are costly：the effect of class distribution on tree induction[J].Jounal of Artificial Intelligence Research，2003，19：315-354.

[17]Chawla N V，Bowyer K W，Hall L O，et al.SMOTE：synthetic minority over-sampling technique[J].Journal of Artificial Intelligence Research，2002，16（1）：321-357.

[18]Han H，Wang W Y，Mao B H.Borderline-SMOTE：a new over-sampling method in imbalanced data sets learning[C]//Proceedings of International Conference on Intelligent Computing，2005，3644：878-887.

[19]He H，Bai Y，Garcia E A，et al.ADASYN：Adaptive synthetic sampling approach for imbalanced learning[C]//ProceedingsofIEEE InternationalJointConference on Neural Networks，2008：1322-1328.

[20]蔡晓妍，戴冠中，杨黎斌.谱聚类算法综述[J].计算机科学，2008，35（7）：14-18.

[21]Verma D，Meila M.A comparison of spectral clustering algorithms[R].Washingtong DC：Department of CSE，University of Washington，2005.

[22]Steinberg D，Colla P.CART：classification and regression trees[M].San Diego，CA：Salford Systems，2009：179-201.

[23]Nickerson A，JapkowiczN，MiliosE.Using unsupervised learning to guide resampling in imbalanced data sets[C]//Proceedings of the 8th International Workshop on Artificial Intelligence and Statitsics，Florida，2001：261-265.