无人机遥感影像镶嵌技术综述

朱 锋，肖 晖，魏亚男

ZHU Feng1,XIAO Hui2，3,WEI Yanan1

1.南京航空航天大学 航天学院，南京 210016

2.南京晓庄学院 生物化工与环境工程学院，南京 211171

3.安徽大学 资源与环境工程学院，合肥 230601

1.College of Astronautics,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China

2.School of Biochemical and Environmental Engineering,Nangjing Xiaozhuang University,Nanjing 211171,China

3.School of Resources and Environmental Engineering,Anhui University,Hefei 230601,China

1 引言

无人机低空遥感系统已成为人们日益关注的研究领域，广泛应用于精确打击、军事侦察、快速数字城市建模、灾害救急等国防和国民经济建设中[1-3]。由于获取图像时受到无人机飞行高度和相机焦距的限制，造成无人机影像像幅小，单张影像无法完全包含感兴趣的区域[4]，为了得到更多目标区域的信息，需要对无人机影像进行镶嵌。而无人机自身质量较轻、气流影响大，使其在空中的姿态很不稳定，导致获取的影像存在很大的畸变，这给无人机影像的镶嵌造成很大的困难[5]。

本文首先介绍了无人机影像镶嵌的关键问题，归纳了国内外无人机影像镶嵌的方法，重点阐述了基于对偶四元数的POS辅助空中三角测量的原理，并且展望了该方法的前景。

2 无人机影像镶嵌问题的描述

影像镶嵌是指不同影像几何纠正到统一坐标系下，去掉重叠部分拼接成具有地理信息的大幅面影像的过程，其主要步骤有：

（1）影像匹配：通过一定的匹配算法在两幅或多幅影像之间识别同名点。主要有基于灰度的匹配和基于特征的匹配。

（2）几何纠正：根据影像的内方位、外方位元素与数字地面模型，利用相应的构像方程式，或按一定的数学模型用控制点解算，确定影像坐标和地面坐标之间的关系，从原始非正射投影的影像获取正射影像，并将其归化到统一的坐标系中。常见的几何纠正模型有多项式纠正、仿射变换纠正和共线方程纠正等。几何纠正产生的误差在很大程度上决定了镶嵌的精度。

（3）亮度和反差调整：去掉重叠部分后“缝合”成为新的大视图影像。由于影像之间存在灰度差异，会导致镶嵌的影像出现接缝，需要对影像进行色调调整。

3 无人机影像镶嵌方法

3.1 多项式法

Yue Yujuan[6]基于SIFT特征匹配进行影像拼接，在基于二次多项式对拼接后影像进行几何校正，均匀选取控制点20个左右校正后的检查点中误差为1.65 m，拼接结果与地形图叠加目视效果良好。

3.2 卡尔曼滤波法

Fernando[7]等提出一种基于卡尔曼滤波的影像局部配准方法，先通过基于特征的影像匹配和地形平坦的假设，计算影像的单应性矩阵及其协方差矩阵，按照金字塔分级匹配的原理，逐步迭代求出精确的单应矩阵，单应矩阵的协方差作为一个参数传到接下来的影像拼接中，从而减少漂移误差的累计。算法优化后每幅影像采样点的位置同GPS数据对比，平均误差为1.76 m。但是，该方法只试用于平坦地区的拼接。Cheng Xing[8]等提出一种改进的卡尔曼滤波方法，再通过L-M算法进行全局优化，以修正重采样影像的位置。局部优化后检查点中误差由1.16 m减小到1.09 m，全局优化后更降低至1.06 m。

3.3 基于SfM点云匹配的方法

Turner等[9]使用特征匹配和SfM摄影技术对无人机影像进行几何纠正和镶嵌，先对影像进行处理，得到模型空间的三维点云，再通过相机位置数据直接定位技术或者获取精确的地面控制点（GCP）坐标，将点云转换到实际的地理坐标系中，生成数字地面模型，最后将具有地理信息的影像进行镶嵌。通过量测地面控制点在镶嵌后影像的平面坐标，并与相应点的GPS数据对比，地面控制点的平面位置最大残差分别为1.2 m（直接定位技术）和0.15 m（GCP技术）。

3.4 传统空中三角测量法

张永军[10]采用传统空中三角测量的方法，先对无人机影像进行匹配，利用匹配获得的同名点进行相对定向，加入地面控制点和检查点进行区域网平差工作，利用平差以后的方位元素，将经过密集影像匹配后的大量同名点进行前方交会生成DEM，进而采集对应的正射影像。通过量测地面控制点在正射影像的平面坐标，并与已知坐标对比，地面控制点的平面误差约为0.03 m。

3.5 POS辅助的空中三角测量法

传统空中三角测量法精度较高，需要提供足够数据的分布均匀的地面控制点。然而由于地面特征不明显、人员无法到达，地面控制点的获取往往比较困难甚至根本不可能。随着全球定位技术和惯性导航技术的迅速发展，定位定向系统（Position&Orientation System，POS）能获取摄站三维坐标和姿态信息，POS系统是由差分全球定位系统（Difference Global Positioning System，DGPS）和惯性测量装置（Inertial Measurement Unit，IMU）组合而成的，能够实现POS辅助的空中三角测量，同时减少或不需要地面控制点[11]。使用该方法对航空影像进行实验，检查点的平面误差约为0.12 m[12]。

3.6 对偶四元数的POS辅助空中三角测量

龚辉[13]提出一种基于单位对偶四元数的航空影像区域网平差解算方法，将影像的摄站位置和姿态以一个单位对偶四元数整体表示，从而构建基于对偶四元数的区域网平差模型，并采用具有约束条件的参数平差进行解算。结果表明，该方法的平差精度与常规的区域网平差方法相当，同时由于无需设置计算的初始参数，计算速度快，具有很好的适应性和稳定性。姬亭[14]按照不同倾角模拟影像数据，分别采用欧拉角法和对偶四元数法进行实验，从定向精度和对不同倾角的适应性进行分析，对偶四元数算法具有明显优势。因此，用对偶四元数进行无人机影像统一的位姿描述，建立POS辅助的光束法平差模型，对进一步提高无人机影像几何定位的可靠性、稳定性以及定位精度实现具有重要的理论意义。

4 对偶四元数的POS辅助空中三角测量原理介绍

4.1 POS辅助空中三角测量原理

带POS系统的中心投影成像原理如图1所示。若a在像平面坐标系o-xy中的坐标为(x，y)，对应的地面点在以M为原点的物方坐标系M-XYZ中的坐标为(X，Y，Z)，航摄仪投影中心 S在 M-XYZ中的坐标为(XS，YS，ZS)，则满足共线方程：

图1 带POS系统的中心投影成像原理示意图[11]

式中，f为航摄仪焦距，a1，a2，…，c3为旋转矩阵 R的九个方向余弦。

由于GPS天线安装过程中，天线相位中心不可能与航摄仪摄影中心完全重合，它们之间总存在着一个空间偏移，通常称为偏心分量。若A在M-XYZ中的坐标为(XA，YA，ZA)，偏心分量为(uA，vA，wA)，则：

同样是由于安装工艺上的限制，IMU与航摄仪不能完全平行而导致相应坐标轴存在微小的方向偏差，即偏心角。若IMU测定的航摄仪姿态角为 φ′，ω′，κ′，偏心角为 φI，ωI，κI，则：

式中 RIMU=Rφ′Rω′Rκ′，RB=RφJRωJRκJ。

4.2 对偶四元数POS辅助空中三角测量

设无人机影像位姿参数的对偶四元数[9]描述为：

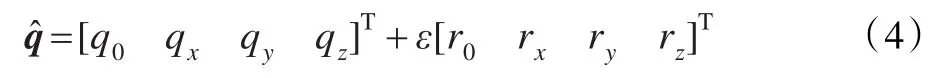
则角方位元素可用对偶四元数的实部表示，线方位元素需以对偶四元数的实部和对偶部分共同表示：

将式（5）代入式（1）～（3）中，得到基于对偶四元数的POS辅助光束法区域网平差的基础误差方程，其矩阵形式可写为：

式中 VX，VC，VG，VI和 LX，LC，LG，LI分别为像点坐标、地面控制点坐标、GPS摄站坐标和IMU姿态角观测值的改正数向量和残差向量，PX，PC，PG，PI分别为各观测值权矩阵；

x=[ΔX ΔY ΔZ]T为待定点坐标未知数增量向量；t=[Δq0ΔqxΔqyΔqzΔr0ΔrxΔryΔrz]T为对偶四元数各分量增量向量；r=[Δu Δv Δw]T为偏心分量未知数增量分量；m=[ΔφIΔωIΔκI]T为偏心角未知数增量分量；Bx，Ax，AG，AI，R，M 为对应的系数矩阵。

由于采用对偶四元数描述影像外方位元素，每张影像存在对偶四元数满足的两个约束条件：

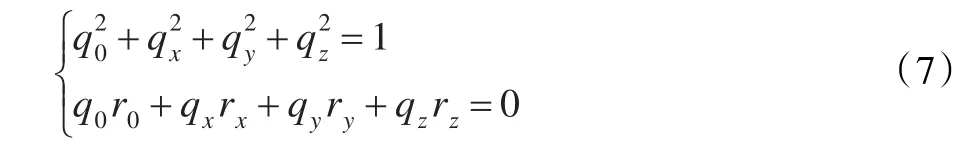
对其线性化，可得约束条件方程为：

式中，

由于通过 R和(XS，YS，ZS)的对偶四元数统一求解可克服外方位元素之间的强相关性[13-15]，因此必将大大提高空中三角测量的解算精度。目前，利用对偶四元数进行POS辅助空中三角测量仍在理论研究阶段，仍需实验评价其精度。

5 结论与展望

（1）随着控制技术、成像技术和计算机技术的发展，新的方法在不断涌现，以下是仍然值得关注的问题：无人机易受到风力等因素的干扰，对影像数据的获取影响较大，需要增加硬件的稳定性能；由于成本和飞行重量的限制，无人机携带的POS系统的精度需要进一步提高，减少对地面控制点的依赖，以提升无人机影像镶嵌的精度以及自动化程度；对于大数据量的无人机影像的高分辨率的快速处理仍然是一个研究的重点，处理大数据量的无人机遥感影像镶嵌软件研发也是一个亟待解决的问题。

（2）POS辅助空中三角测量无需或者只需少量控制点就能达到较高的精度，大大降低了野外工作量。由于对偶四元数描述影像的位置和姿态具有适应性强的优势，利用对偶四元数建立POS辅助的空中三角测量模型，将是无人机影像镶嵌的一个新的发展方向。

[1]Albert R，Andrea L，Jeffrey H，et al.Unmanned aerial vehicle-based remote sensing for rangeland assessment，monitoring and management[J].Journal of Applied Remote Sensing，2009，3（1）.

[2]贾娇，艾海滨，张力，等.应急响应中PixelGrid无人机遥感数据处理的关键技术与应用[J].测绘通报，2013（5）：62-65.

[3]吴亮，赵西安.基于DPGrid系统的无人机遥感数据处理试验[J].北京建筑工程学院学报，2013，29（1）：43-48.

[4]王琳.高精度、高可靠的无人机影像全自动相对定向及模型连接研究[D].北京：中国测绘科学研究院，2011.

[5]洪宇，龚建华，胡社荣，等.无人机遥感影像获取及后续处理探讨[J].遥感技术与应用，2008，23（4）：98-102.

[6]Yue Yujuan，Li Dongliang，Li Ying，et al.Discussion on the mosaic and geometric correction technique of UAV remote sensing image[C]//The International Conference on Mechanic Automation and Control Engineering.Beijing，China：IEEE Computer Society，2010：4528-4530.

[7]Caballero F，Merino L，Ferruz J，et al.Homography based kalman filter for mosaic building application to UAV position estimation[C]//International Conference on Robotics and Automation，Roma，Italy，2007.

[8]Xing Cheng，Wang Jinling，Xu Yaming.A robust method for mosaicking sequence images obtained from UAV[C]//2nd International Conference on Information Engineering and Computer Science，Wuhan，China，2010.[S.l.]：IEEE Computer Society，2010：1-4.

[9]Turner D，Lucieer A，Watson C.An automated technique for generating georectified mosaics from ultra-high resolution unmanned aerial vehicle imagery，based on Structure from Motion（SfM）point clouds[J].Remote Sensing，2012，4（5）：1392-1410.

[10]张永军.无人驾驶飞艇低空遥感影像的几何处理[J].武汉大学学报：信息科学版，2009，34（3）：284-288.

[11]韩文超.基于POS系统的无人机遥感图像拼接技术研究与实现[D].南京：南京大学，2011.

[12]袁修孝.POS辅助光束法区域网平差[J].测绘学报，2008，37（3）：342-348.

[13]龚辉，姜挺，江刚武，等.利用单位对偶四元数进行航空影像区域网平差解算[J].武汉大学学报：信息科学版，2012，37（2）：154-159.

[14]姬亭，盛庆红.对偶四元数单片空间后方交会算法[J].中国图象图形学报，2012，17（4）：494-503.

[15]盛庆红，姬亭，刘微微，等.对偶四元数线阵遥感影像几何定位[J].中国图象图形学报，2012，17（10）.