改进多尺度特征提取的图像配准算法研究

杨宇光 ，滕义伟

YANG Yuguang1，2,TENG Yiwei1

1.北京工业大学 计算机学院，北京 100124

2.西安电子科技大学 综合业务网国家重点实验室，西安 710071

1.School of Computer Science,Beijing University of Technology,Beijing 100124,China

2.The State Key Laboratory of Integrated Services Networks,Xidian University,Xi’an 710071,China

1 引言

图像配准是图像处理领域的一项关键技术[1]，它在图像融合、遥感影像分析、医学图像分析以及计算机视觉等应用中发挥着重要的作用。特征提取和匹配是图像自动配准的两大难点。利用多尺度采样理论提取各种特征点具有尺度和仿射不变的特性，为图像特征提取和匹配提供了良好的途径。Lowe[2-3]提出了尺度不变特征变换（SIFT）特征点提取算法，被广泛应用于特征匹配中，具有稳定的旋转和尺度不变性。Mikolajczyk[4-5]和Schmid[5]提出的Harris-Laplace特征提取算法在位置可重复性、定位精确度、尺度不变性等方面均有较好的性能。

由于一幅图像的局部结构可能在一定的尺度范围内被多次检测到，产生大量的冗余点[6]。这些冗余点在检测时得到的位置和尺度会有一些差异，降低了图像的配准精度导致误匹配产生。为了去除冗余点，本文首先在特征点检测阶段通过对多尺度检测到的图像特征点在其邻域内进行筛选，然后选取最具代表性的唯一特征点作为最终的特征点来表示这一个局部结构。实验表明，本文改进的算法相较于原来的Harris-Laplace算法检测到的特征点分布更均匀并且获得匹配点的数目更稳定。同时，实验结果表明本文算法具有更高的图像配准的速度和精度。

2 Harris-Laplace特征检测及存在的问题

2.1 Harris-Laplace算法

2.1.1 构建尺度空间

尺度空间表示一个平滑图像集，它是由输入图像和可变尺度的高斯核函数进行卷积运算得到的。Lindeberg[7]已经证明高斯核函数是尺度空间的唯一表示。

2.1.2 检测Harris-Laplace特征点

由于二阶矩阵描述一个点在邻域内的梯度分布，所以它经常用来进行特征点的检测。归一化的尺度空间微分表示，如下：

其中，

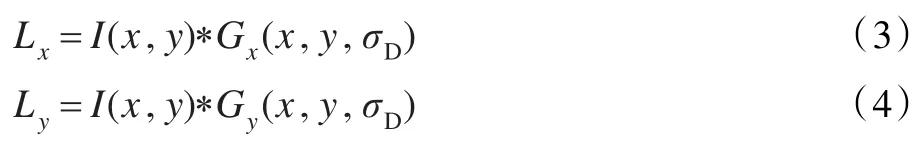
在公式（2）～（4）中，x，y为图像中的坐标点，σI，σD分别表示积分尺度和微分尺度，σD=sσI是一个标量。一般来说，积分尺度要比微分尺度大。在本文中，s取0.7。I(x，y)为输入图像。通过公式（4），计算每个尺度空间图像上点的响应值，并将满足条件的点作为特征点[8]。

α是一个常量，一般取值范围为0.04～0.06。Threshold为预设阈值，控制提取的特征点数目。

2.2 存在的问题

基于多尺度的特征检测存在如下问题：一幅图像中的局部结构可以在一定尺度范围内检测到。所以对于同一个局部结构将会检测到多个特征点，但是这些特征点的在尺度和位置上很小的差别，将在后续匹配时产生误匹配，同时增加了计算的时间复杂度。

图1是北京工业大学国际交流中心的图像，使用Harris-Laplace算子提取图像的特征点的结果如图1（a）所示。将图1（a）中黄色框内图像放大得到图1（b）。其中，绿色•表示提取的图像的特征点，红色○表示对应特征所在的尺度。从图1（a），（b）中可以看到，一个绿•同时被多余一个不同半径圆圈住，即每一个局部结构都会在不止一个尺度上检测到，这将增加冗余点的数目并增加在特征匹配阶段特征点匹配的复杂度。同时，由于同一局部结构的特征点微小的差异将会增大误匹配的概率。怎么从同一个局部结构所产生的特征点中选取最有代表性的特征点，从而减少冗余点，降低计算复杂度，同时减少图像配准中的误匹配，这个问题是本文改进算法讨论的重点。

图1 Harris-Laplace特征点检测

3 改进的Harris-Laplace特征提取及图像配准算法

3.1 尺度空间检测Harris特征点

首先，根据公式（1），通过不同尺度的高斯核函数和输入图像作卷积生成尺度空间。然后，利用公式（2）～（5）检测出每个尺度空间上所有的特征点。

3.2 选择最优特征点

实验证明，表示相同局部结构的特征点总是集中在一个特定的尺度范围内，并且一般来说相邻尺度的两个兴趣点的距离在1～3个像素内，如图1（b）所示，即在一定区间内表示相同局部结构的所有特征点在位置和尺度上只有较小的差异。同时，在尺度空间内角点越接近真正的角点，说明该点邻域的灰度值变化越大，也即是该特征点的角点响应值越强。所以，可以对尺度空间内提取的所有特征点通过统计滤波，求取角点响应值最大的特征点作为最终的候选特征点，实现冗余点的剔除。具体算法如下：

（1）构造选择模板MASK。构造一个二维矩阵MASK(m，n)，矩阵中每个元素是由点对(response，scale)构成。初始化 MASK(i，j)={0，0}，其中 0≤i＜m，0≤j＜n，m，n为原图像 I(x，y)的大小。

（2）从高尺度图像开始提取特征点赋值给对应位置上的MASK点对。由于高斯核函数的尺度越大，经高斯核函数平滑后的图像纹理变得越稀疏，能够检测得到的特征点也越少且分布均匀。所以从高尺度图像开始对MASK进行赋值，这样比较容易确定MASK最终选择值。所以，先提取高尺度图像中的特征点，并将特征点的响应值 Response(x，y，σ)赋值给对应 MASK(x，y)点对。

（3）提取相邻尺度图像上的特征点。从高尺度图像开始，依次提取相邻低尺度图像上的特征点。重复步骤（2），直到所有尺度图像上的特征点赋值给模板MASK。如果模板相同位置出现不同尺度上检测到的两个兴趣点，则选择较大 Response(x,y,σ′)值点赋值给MASK(x，y)。

（4）利用统计滤波器筛选兴趣点。由于表示相同局部结构的特征点总是集中在一个特定的尺度范围内，并且一般来说相邻尺度的两个兴趣点的距离在1～3个像素内，即在一定区间内表示相同局部结构特征的所有特征点在位置和尺度上只有较小的差异。因此可以利用半径为3的统计滤波器对模板MASK进行滤波，分别求得每一点处角点响应的最大值Max(x，y)和角点响应次大值 Second(x，y)。如果 Max(x，y)＞Second(x，y)，且满足 Max(x，y)=MASK(x，y)则记录下该点坐标。

（5）生成最终的特征点。由步骤（4）计算得到的所有特征点是已经剔除了表示相同局部结构冗余点。它们是图像局部结构特征的唯一表示。保存这些特征点的尺度、函数响应值，将求得的点作为最终表示局部结构的最优的特征点。

通过对Harris-Laplace算法的改进，在检测阶段剔除大量的冗余点，减少了后续的匹配操作，节省了大量不必要的复杂计算，提高了配准速度。同时，剔除的冗余点减少了对匹配过程的干扰，所以改进的Harris-Laplace算法提高了图像配准的精度。

3.3 特征描述

为了实现特征准确匹配，每个特征点的描述要尽可能得充分：不同的特征点要具有明显的差异性，匹配的特征点对要有充分的相似性。Lowe在研究SIFT[2，9-10]算法时，通过实验证明，128维的SIFT描述子具有很好的旋转不变性。所以在本文采用SIFT描述子对特征点进行描述。SIFT描述子生成过程如下：

（1）为待配准的特征点分配主方向。在特征点的附近创建方向收集区，收集区域的大小依赖于特征点所在图像的尺度。尺度越大的图像中检测出的特征点，对应的收集区域也越大。根据公式（6）、（7）计算收集区域中每个像素点的梯度大小和方向。在0～2π范围内，建立n bin的梯度直方图，则第i bin表示方向在2(i-1)π/n～2i π/n，i=1，2，…，n范围内的像素。像素的梯度大小加到该像素方向对应的bin上。所得直方图的最大值位置为主方向所在的相位，将它分配给特征点。如果n过大，使梯度直方图过于分散，影响峰值的确定；如果n过小，则使得主方向精度过低，不能正确描述主方向。综合以上两种情况，本文实验中n取36。

（2）计算特征点邻域的种子点。选取特征点为中心的16×16邻域，将该邻域平均分成16个大小为4×4的子区域。同步骤（1）在每个子区域中，生成一个8 bin的梯度直方图。直方图中每个bin的大小不但与对应像素点的梯度相关，而且还依赖于该像素点到特征点的距离。选取高斯函数G(x，y，σ/2)为加权函数，其中σ为该特征点的尺度值。对每一个区域中的直方图进行卷积运算，如公式（8）所示。

（3）描述子归一化。通过步骤（2）计算，每个子区域由一个8维向量来表示。那么一个特征点则由16×8=128维的向量表示。为了使该描述子具有光照不变性，需要再对其进行向量归一化操作。

3.4 特征点匹配

图像的特征点匹配是指将不同图像中的不同点对应于物理空间中的相同点。所以，只要找出了参考图像特征点与目标图像特征点间的匹配关系，就能根据特征点的坐标求解图像变换模型的参数。特征点匹配的原理是检测不同图像特征点之间的欧氏距离（Euclidean distance）。一个特征点的最佳匹配点应该是欧氏距离最小的点。SIFT特征点的欧氏距离计算如下：

d(pi)，d(pj)分别表示特征点 pi，pj的不变特征向量。由于有些特征点没有在参考图像中检测出来，或者是根本就不存在于参考图像中，所以目标图像中的很多特征点在参考图像对应的点存在。所以，必须要判断一个特征点是否有匹配点。更有效的方法是根据公式（10）计算特征点的最小欧式距离点与次最小欧式距离点的距离的比值：其中，d(pi，pj)是最小欧式距离，d(pi，pk)是次最小欧式距离。

如图2所示，如果比值r大于0.7，意味着不存在最佳匹配点，也就是 pi点在参考图像中没有可匹配的特征点存在。此时可认为 pi是无匹配的点，应将其排出特征点集合。所以可以设定匹配阈值为0.7，如果比值r大于0.7，则该点没有最佳匹配点；否则认为该点的最佳匹配点即为它的最小欧氏距离匹配点。

图2 特征点欧式距离比值[2]

4 图像配准实验结果分析

本文主要从图像缩放，旋转，光照方面对基于Harris-Laplace的图像配准算法和文中提出的基于改进Harris-Laplace的图像配准算法性能进行了实验对比。实验的对比参数包括两种算法分别检测到的特征点数目、匹配点数目、图像配准时间消耗、剔除冗余点数目、匹配效果。

本文实验所用图像为北京工业大学国际交流中心大楼，参考图像为273×377×3大小的jpg格式的图像，目标图像为214×222×3大小的jpg格式图片。工作平台配置：Lenovo THINKPAD E40，处理器 Intel®CoreTMi5，内存2 GB，32位操作系统，Matlab R2010b。

4.1 图像缩放配准实验及分析

由图 3（a）、（b）可以看出，基于 Harris-Laplace算法的提取的特征点存在大量的同心圆和临近点。这些同心圆和邻近点是由于相同的局部特征结构在多个尺度上被检测到所导致的。基于原始Harris-Laplace算法的特征提取产生了大量的冗余点，尤其对于纹理丰富的图像产生的冗余点会更多。在图像配准过程中要对提取的特征点进行特征描述和特征点匹配，检测中产生的冗余点在后续图像配准过程中将消耗大量的时间，同时也增加了误匹配的可能。基于原算法的图像配准效果如图3（c）所示，在图中可以看到有一部分误匹配的交叉线。与上面的图3（a）、（b）对比，基于改进Harris-Laplace算法提取的特征点如图4（a）、（b）所示，消除了同心圆和邻近点并且特征点分布更均匀。基于改进算法的图像配准效果如图4（c）所示，从图中可以看到匹配点的连线没有交叉的误匹配点对。对照图3和图4，可以明显看出在（a）、（b）子图中图4比图3所提取的特征点更均匀；在（c）子图中，图4中交叉的蓝线也比图3少，即误匹配点少。将目标图像进行不同倍数的缩放后，得到的图像配准实验数据如表1所示。

对表1数据进行处理得到图5。从图5（a）中的红色实线和绿色实线可以看到，随着目标图像尺寸的变大无论原Harris-Laplace算法检测到的特征点数目还是改进的Harris-Laplace算法检测到的特征点数目都在增加。这是由于目标图像在尺寸放大的过程中经过双三次插值使得图像中每个像素间差异更小。这将导致检测到更多的同心圆点和邻近点如图5（a）所示，黑色实线随图像尺寸变大也在增加。从图5（a）中的红色虚线和绿色虚线可以看到，红色虚线和绿色虚线非常接近。绿色虚线在除两端位置外基本呈现一条直线，波动较小；红色虚线相对绿线有较大的波动。这说明改进的算法对于图像缩放变换有更好的稳定性。从图5（b）中的红色实线和绿色实线可以看出，基于改进算法的图像配准具有更快的配准速度。这是由于改进的算法虽然在剔除冗余点的过程中消耗一部分时间，但是由于冗余点剔除避免了在特征描述和特征匹配过程中的时间消耗，所以在总体图像配准过程中时间消耗要明显少于原来的算法，具有较高的匹配速度。

图3 缩放：基于Harris-Laplace的特征提取及配准

图4 缩放：基于改进算法的特征提取及配准

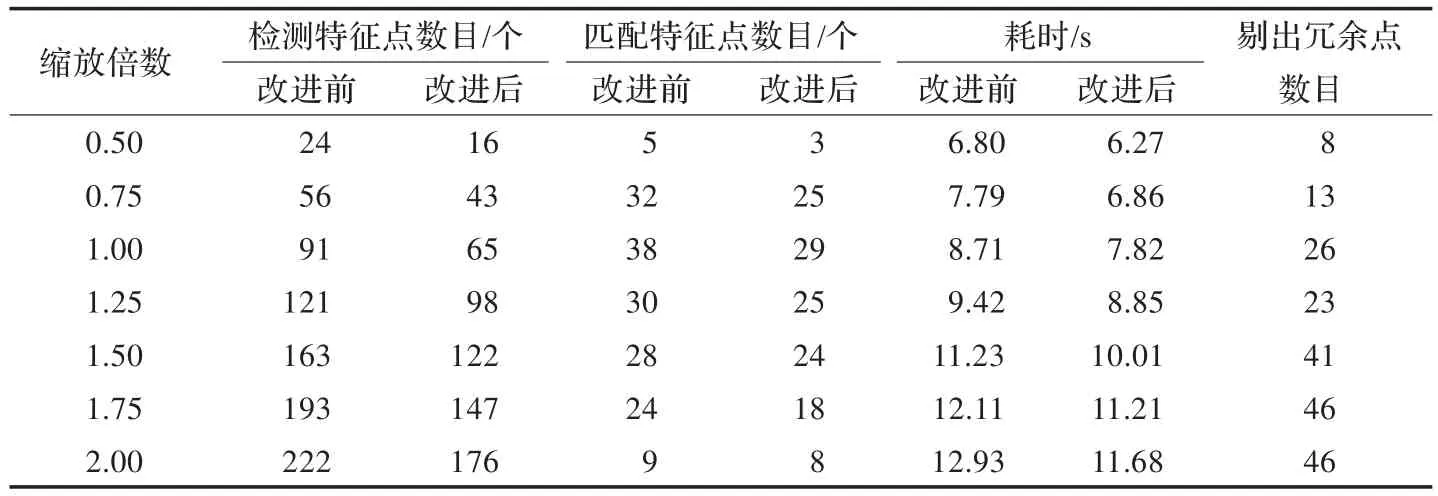
表1 目标图像缩放后图像配准实验数据

图5 目标图像缩放变换后两种算法的性能分析

4.2 光照变化后图像配准实验及分析

图6（b）和图7（b）是在强光环境下获取的图像。对比图 6（b）和图7（b）可以发现，利用原 Harris-Laplace算法提取特征的图6（b）上出现了大量的冗余同心圆点和邻近点；图7（b）上的特征点没有同心圆及邻近点，并且提取的特征点分布比较均匀。从配准效果上看，基于改进Harris-Laplace算法如图7（b）较基于原Harris-Laplace算法如图6（b），由于改进算法图像配准所匹配的特征点无重合点并且分布均匀，所以可以得到更准确的图像变换参数。除此之外，基于改进的图像配准较基于原算法在时间消耗上更少，如表2所示。因此在光照影响条件下与基于原算法的图像配准相比，基于改进Harris-Laplace算法的图像配准具有配准精度高、速度快、鲁棒性强等优点。

图6 光照：基于Harris-Laplace的特征提取及配准

图7 光照：基于改进算法的特征提取及配准

4.3 图像旋转配准实验及分析

从图 8（b）和图9（b）中可以看到，由于目标图像的旋转在目标图像的边缘形成了锯齿状的毛边，在图像的边缘处将检测到大量的角点。对比基于原算法提取特征的图8（b）和基于改进算法的图9（b），可以明显看出图8（b）中存在大量同心圆和邻近点并且在边缘上也存在较多角点，导致形成大量的冗余点；图9（b）中不但抑制了旋转图像中同心圆和邻近点，同时也抑制了边缘点的产生。从总体上看，图9（b）比图8（b）特征点分布更均匀，可分辨性更强，误匹配的可能更小。从图8（c）和图9（c）两种算法的配准效果上看，图8（b）中存在多个邻近点与多个同心圆点匹配的情况，这将在获取图像变换参数产生误差，从而降低图像配准的精度；图9（c）中由于对同心圆点和邻近点的抑制使得特征点定位更精确。同时由于图9（c）中匹配点分布均匀，所以可以获得更精确的图像变换参数，提高图像的配准精确度。对目标图像进行不同角度旋转后，得到的图像配准实验数据如表3所示。

将表3数据进行处理生成图10。从图10（a）中可以看到，红色实线和绿色实线随着目标图像旋转角度的变化有较大的波动。这是由于图像旋转出现了不同程度的锯齿状毛边，这直接影响检测到的特征点数目。从图10（a）中的红色虚线和绿色虚线可以看出，虽然Harris-Laplace算法和其改进算法在检测得到的特征点数目上有较大的差异，但是基于两种算法匹配的特征点数目相差不大。对比图10（a）中的绿色虚线和红色虚线的波动情况，绿色虚线基本呈现一条直线，波动性较红色虚线非常小。这说明基于改进Harris-Laplace图像配准算法具有更好的稳定性。同时，图10（a）中的黑色实线反映了改进算法对同心圆和邻近特征的点良好抑制功能。从图10（b）中可以看到，基于原算法的图像配准所消耗时间和基于改进算法的图像配准所消耗的时间都随图像旋转角度的变化有较大的波动，但是绿色实线始终在红色实线下方并保持较大的距离。这说明基于改进Harris-Laplace图像配准算法相较于原来的算法具有更快的配准速度。

表2 目标图像不同光照强度下图像配准实验数据

图8 旋转：基于Harris-Laplace的特征提取及配准

图9 旋转：基于改进算法的特征提取及配准

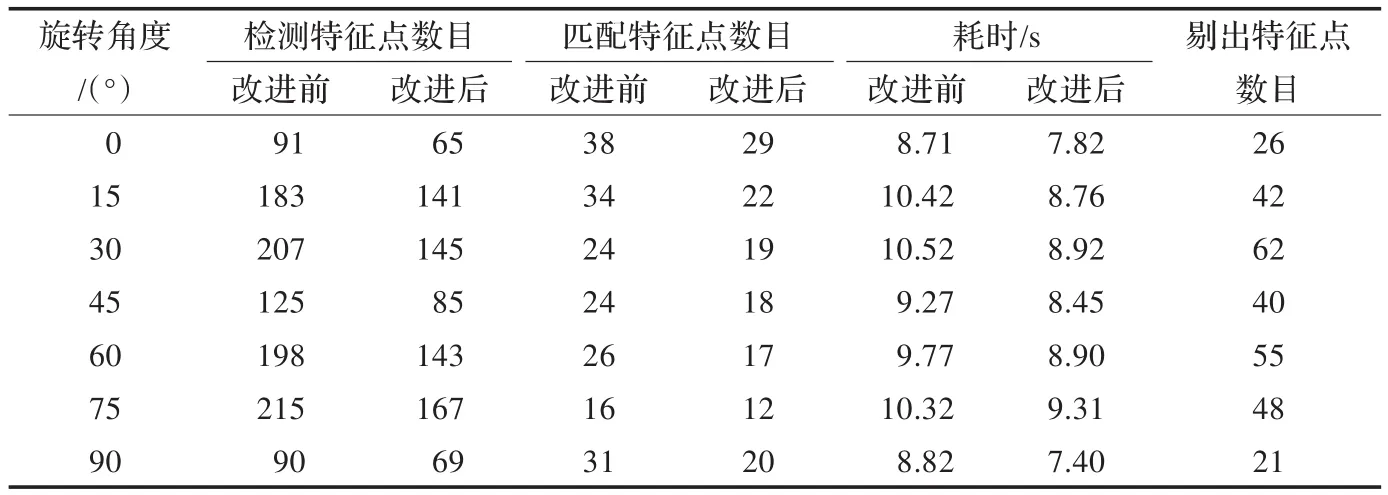
表3 目标图像旋转后图像配准实验数据

图10 目标图像旋转变换后两种算法的性能分析

5 结束语

本文提出的改进算法主要解决了图像中的局部结构合理表示的问题，并在检测阶段剔除冗余特征点，提高图像的配准速度、稳定性。由于一幅图像的局部结构利用Harris-Laplace在多尺度上进行特征检测时，这个局部结构可能在一定的尺度范围内被检测到。但是表示相同局部结构多个特征点在位置或尺度会有一些差异，这些产生的冗余点将在特征匹配时导致误匹配。本文通过对检测到的候选特征点在其邻域内与其他候选特征点的响应值比较，选取最大响应值的点来表示这个局部结构。通过这种改进，剔除了表示同一局部结构的其他冗余点。改进算法从图像缩放变换、光照变化、旋转变换三个方面和基于原来算法的图像配准进行了对比。从得到的实验数据可以看到，改进的Harris-Laplace算法不仅延续了原始Harris-Laplace算法固有的旋转不变性、尺度不变性和特征点分布均匀等诸多优点，而且在图像发生缩放变换、光照变化和旋转变换后仍能检测到比原算法更稳定的特征点。同时，本文采用SIFT描述子对检测到的特征点进行描述。这使得生成的描述子具有良好的独特性，从而提高了特征点匹配准确性。大量的实验结果表明，基于改进Harris-Laplace特征提取的图像配准算法相较于未改进算法不仅具有更好的旋转、光照和尺度不变性，还能较稳定获取匹配点。同时由于本文算法在特征检测减少了冗余点数目，避免了对冗余点的特征描述和匹配，减少了计算的复杂度，提高了图像配准的匹配速度和匹配精度。

[1]李伟生，王卫星，罗代建.用Harris-Laplace特征进行遥感图像配准[J].四川大学学报：工程科学版，2011，43（4）：89-95.

[2]Lowe D G.Distinctive image features from scale-invariant keypoints[J].International Journal of Computer Vision，2004，60（2）：91-110.

[3]Lowe D G.Object recognition from local scale-invariant feature[C]//International Conference on Computer Vision，Corfu，Greece，1999：1150-1157.

[4]Mikolajczyk K.Detection of local features invariant to affine transformations[D].France：Institut National Polytechnique de Grenoble，2002.

[5]Mikolajczyk K，Schmid C.An affine invariant interest pointdetector[C]//European Conference on Computer Vision（ECCV），2002：128-142.

[6]Zhang Jieyu，Chen Qiang.A highly repeatable feature detector：Harris-Laplace[J].Multimed Tools Appl，2011，52（1）：175-186.

[7]Lindeberg T.Scale-space theory：a basic tool for analysing structures at different scales[J].Journal of Applied Statistics，1994，21（2）：224-270.

[8]Harris C，Stephens M.A combined corner and edge detector[C]//Fourth Alvey Vision Conference，1988：147-151.

[9]Brown M，Lowe D.Recognising panoramas[C]//Proceedings of the 9th International Conference on Computer Vision，2003：1218-1227.

[10]Gonçalves H，Corte-Real L，Gonçalves J A.Automatic image registration through image segmentation and SIFT[J].IEEE Transactions on Geoscience and Remote Sensing，2011，49（7）：2589-2600.