全尾砂胶结充填体弹塑性本构模型实验研究

吴 姗 宋卫东 张兴才 周家祥

(1.北京科技大学土木与环境工程学院，北京100083;2.金属矿山高效开采与安全教育部重点实验室，，北京100083;3.武汉钢铁集团矿业有限责任公司，湖北武汉430080)

随着地下充填采矿法应用比例的逐步提高，充填体力学逐渐形成岩石力学的一门分支学科。充填体力学是岩石力学、土力学和流体力学等在充填采矿中的综合运用［1］。尾砂胶结充填体为尾砂和胶凝剂组成的多相复合材料，其内部包含有各种微裂纹、微孔隙、气泡等，有不同于岩石和混凝土的独特力学特性［2］。影响尾砂胶结充填体强度的因素有胶结剂种类与其加入量、充填料浆浓度、尾砂级配组成、搅拌时间、养护龄期、养护环境及尾砂化学成分等［3］。采用全尾砂胶结充填可以减少尾矿排放，是充分利用尾矿资源发展节地、节能、节材和环保利废的直接有效途径［4-5］。

充填体稳定性是一重要的研究课题，直接关系到回采贫化损失率与采矿的安全［6］。目前普遍采用充填体单轴压缩对充填体强度进行研究［7-8］，而工程实际中充填体的单轴受力状态比较少见，三轴受压条件下的变形和强度特征是影响充填体工作性能的重要因素，它决定着充填体的力学强度和稳定性能［4-5］。

本研究采用不同配比及料浆浓度，制备了大冶铁矿全尾砂胶结充填试块，在传统的单轴压缩实验的基础上，得到了全尾砂胶结充填体的基本力学参数，随后通过不同围压下充填体的三轴压缩实验，得到了全尾砂胶结充填体物理力学参数及全应力－应变曲线。同时建立了全尾砂胶结充填体的弹塑性本构模型，为充填体强度设计提供了依据。

1 大冶铁矿全尾砂物理性质

大冶铁矿全尾砂基本物理性质如表1所示，粒级组成如表2所示，可以看出，大冶铁矿全尾砂比表面积比较大，中值粒径D50＜25μm，D90=110μm，属于超细全尾砂。

表1 大冶铁矿全尾砂基本物理性能Table1 Basic physical properties of full tailings for Daye Iron M ine

表2 大冶铁矿全尾砂粒级组成Table2 Particle size composition of full tailings for Daye Iron M ine

2 全尾砂－水泥胶结充填体单轴压缩实验

2.1 实验材料及设备

实验骨料选用大冶铁矿选矿全尾砂，胶结剂为普通标号42.5R水泥，试验模具采用10 cm×10 cm×10 cm标准三联试模，制备料浆浓度分别为65%、68%、70%、72%、75%，灰砂比为1∶4、1∶6、1∶8、1∶10，养护龄期为3 d、7 d、28 d。通过JJ－5型水泥胶砂搅拌机对尾砂和水泥进行搅拌，然后放到YH－40B型全自动标准恒温恒湿养护箱中进行养护，养护温度为20±5℃，相对湿度为(95±5)%。达到养护天数后在电子液压式压力试验机上测定其单轴抗压强度。

2.2 实验结果及分析

通过试验可得到充填试件的载荷位移曲线及试件破坏时的最大载荷和最大位移，4种灰砂比的不同料浆浓度的充填体强度随养护期龄变化的关系一致。以灰砂比1∶8为例(图1)，在养护前期，试件强度增长幅度较大，曲线较陡;但是一定时间之后，试件强度增长放缓，这是由于水泥的水化反应过程主要集中在养护的前期。随灰砂比及料浆浓度的增加，充填试件3、7及28 d的强度呈明显的增长趋势。图2为养护28 d的强度曲线，对充填强度与料浆浓度进行非线性回归，得到回归方程。当灰砂比一定时，充填强度与料浆浓度服从二次方程，且相关性系数R2均大于0.95，拟合度很好。

图1 不同养护期龄充填体单轴抗压强度(灰砂比1∶8)Fig.1 Uniaxial compressive strength of filling body on different curing age(Cement-sand ratio 1∶8)

图2 全尾砂－水泥胶结充填体单轴抗压强度(养护28 d)Fig.2 Uniaxial compressive strength of full tailings-cement filling body

充填体强度与养护期龄、灰砂比、料浆浓度均为正相关。对于一般矿山采空区来说，充填强度达到2.0～3.0 MPa即能满足充填要求［9］，灰砂比1∶6时，浓度大于65%的试件强度都能达到要求;灰砂比1∶8时，浓度为72%的高浓度试件强度才能达到;灰砂比1∶10时，只有浓度为75%的高浓度试件强度能达到。在现场充填系统技术能达到的前提下，采用高浓度充填就可以适当减少水泥用量，加快采场周转，进一步节约成本，提高生产能力。根据实际数据，绘制莫尔强度包络线，得到了各充填试块的黏聚力和内摩擦角，如表3所示。

表3 试块黏聚力和内摩擦角Table3 Values of cohesion and internal friction angle

3 全尾砂－水泥胶结充填体三轴压缩实验

单轴实验主要测定试件在单方向受压时的强度指标，单纯从充填体受力的角度出发，研究充填体的承载能力。而在生产实际中，充填体单纯的单轴受力状态的情况较为少见，多数情况下是处于三轴受力状态。因此，研究充填体在三轴受力条件下的力学特性对探明充填体的破坏机理及其工程实践具有现实意义［10］。

3.1 实验过程

在设计大冶铁矿充填体强度时，参照了国内外类似矿山的经验，按下列充填体高度与强度的经验公式进行验算［11］:

式中，H为胶结充填体矿柱的高度，m;σ为胶结充填体的设计强度，MPa;a为经验系数。

H＜50 m，a=600，则σ=1.61 MPa。故根据充填体单轴抗压强度，选取4组(每组4个)充填试块进行三轴压缩实验:①配比1∶6，浓度65%;②配比1∶6，浓度70%;③配比1∶8，浓度65%;④配比1∶8，浓度70%。试块制作完毕后于恒温养护箱养护28 d至最终强度。

实验采用轴向位移控制，应变速率为1×10－4，三轴压缩试验采用“定围压，加轴压”的方法，先加围压至预定值(0.4、0.6、0.8、1.0 MPa)，然后加轴向力直至试样破坏，得到了充填体在不同围压σ3下的应力－变形量曲线，如图3所示。

3.2 充填体全应力－应变曲线特征分析

如图3(a)所示，充填体的三轴曲线可以分为以下几个阶段:①初始压密阶段(OA)，表现为在很小的应力下发生较大变形，这是由于充填体为人造混合材料，在制作与养护过程中仅靠自身重力压实，其内部孔隙缺陷较大。②线弹性阶段AB，是充填体强度形成阶段，此时充填体内部孔隙闭合完全，应力与应变的增加呈直线关系，此阶段的变形特征可以通过弹性模量和泊松比来描述。③非线性破坏阶段BC，是充填体微裂纹的产生、发育和累积的阶段，从能量的角度来说，线弹性阶段可以认为充填体内部能量积聚，当能量的积聚达到一定程度，即在B点达到极限后，能量开始逐渐释放，充填体开始发生破坏，内部开始形成屈服面。随着屈服面的发育，充填体到达承载极限，在C点达到峰值强度，充填体内部屈服面开始联通。④应变软化阶段CD，充填体逐渐表现出塑性破坏和应变软化现象，到达D点时充填体强度不再发生明显变化，形成残余强度，性状上表现为应变软化状态消失，呈现完全的塑性流动状态。⑤塑性流动阶段DE，随着塑性变形的持续发展，充填体强度不再降低，达到残余强度，这个阶段可以认为是理想的塑性阶段。

图3 充填体全应力－应变曲线Fig.3 Stress-strain curve of filling body

3.3 充填体空间受力破坏特征分析

图3为4种充填体峰值强度与围压的关系曲线，可以看出，围压增大，充填体峰值载荷及塑性变形也增大，峰值强度σc与围压σ3呈显著线性关系，图3 (a)～图3(d)4种充填体的表征关系如图4所示，相关系数R2均较高。

随着围压的增加，峰值强度(σc)与残余强度(σr)之间的差值逐渐缩小(如图5所示)，充填体在达到屈服从而促使充填体由相对的脆性向延性的转化，其性状最终会因足够大的围压而趋于变为完全延性［12］。相对峰值强度而言，充填体的残余强度对围压较敏感。

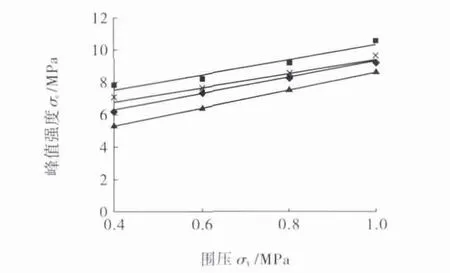
图4 充填体峰值强度和围压的关系Fig.4 Relationship between the peak strength and confining pressure of the filling body

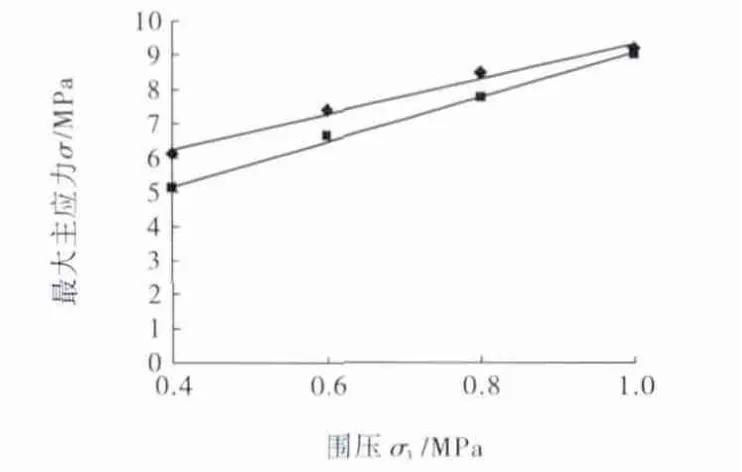
图5 充填体的强度分析Fig.5 The filling body's strength analysis

图6给出了在不同围压下充填试件破裂形式。在低围压(0.4 MPa)时，试件脆性变形特征明显，峰值强度过后应变软化现象明显，应力－应变曲线表现为理想弹塑性曲线特征，岩样破坏形式为共轭斜面剪切破坏，破坏面粗糙不平，侧位移明显呈鼓状，如图6 (a)所示。随围压的增加，应力－应变曲线在峰值强度附近出现平台，而且平台的宽度随围压升高增大，曲线在峰值强度过后，无明显应变软化阶段，直接进入塑性流动状态，峰值强度与残余强度之间的差距减小，试件破坏形式从共轭破坏向剪切破坏过渡，表现为光滑的剪切面伴随局部裂纹，如图6(b)所示。在高围压(1.0 MPa)作用下试件破坏形式为明显单斜面剪切破坏，经测量剪切面法线与荷载轴线夹角β= 63°，与计算所得内摩擦角 φ符合 β=(π/4)+(φ/2)的关系，如图6(c)所示。

围压的增大对充填体力学特性的影响明显。围压增大时，充填体的峰值强度、峰值应变、和残余强度数值均呈增大趋势，而弹性模量却随围压增大而减小。因此充填体在充入井下充填采场后，只有矿柱或围岩紧密接触才能达到最好的充填效果。具体可以通过提高爆破工艺、避免充填死角的产生，优化充填工艺、减少充填体暴露面积和时间等措施来实现。

图6 充填体破坏特征Fig.6 Failure characteristics of the filling body

4 充填体弹塑性本构模型的建立

在三轴压缩过程中，由于初始压密阶段过程短暂，且不能体现充填体主要特征，故第1阶段即压密阶段和第2阶段在一定意义上可以合并为1个阶段，即准线性阶段［13］。故将全应力－应变曲线简化成4个阶段，如图7所示。

图7 充填体典型应力－应变关系曲线Fig.7 Typical stress-strain curve of the filling body

(1)准线性阶段(OA)。应力－应变曲线为一直线，符合广义胡克定律［14］

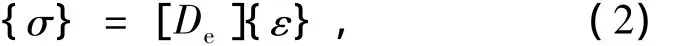
式中，{σ}为应力向量;［De］为弹性刚度矩阵;{ε}为应变向量。

(2)屈服阶段(AB)。根据试件破坏特征分析，可以得出充填体试件在破坏时是受剪应力作用，剪应力小于抗剪强度时，试件表现为屈服状态;当剪应力达到抗剪强度时试件破坏。假定在屈服段开始时，充填体塑性变形量较小，此时仍可将充填体看做弹性的;随着应力的增加，变形持续发展，充填体逐渐达到破坏B点。按照Mohr－Coulomb准则［15］，初始屈服函数可表示为

式中，σ1为轴向压力;σ3为围压;

cs与φs分别为弹性段内聚力与内摩擦角。破坏时的破坏准则可以表示为

式中，

cp与φp分别为峰值内聚力与内摩擦角。假定屈服函数随轴应变ε在fs和fp之间呈线性变化，则有

式中，

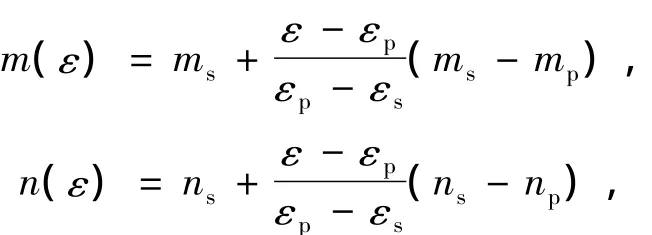
εs和εp分别为屈服应力与峰值应力对应的应变值。根据弹塑性理论［15］及实验加应力路径，由Mises塑性流动法则，可得

式中，f为后继屈服函数;dλ为塑性流动因子。由此可得充填体本构方程

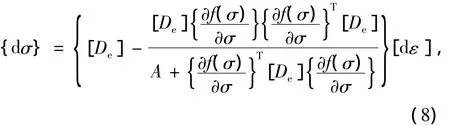
式中，A为硬化模量，与硬化参数的选择有关。

(3)峰后应变软化阶段(BC)。充填体峰后应变软化阶段可分为2种情况:低围压时，表现出明显应变软化，应力脆性跌落;在围压较高时，应变软化不明显。根据Owen D.R.J.给出的公式计算得

式中，ER为软化系数，可以通过屈服函数求得。将式(9)代入式(8)即可得此时应变软化段本构方程。

(4)理想塑形阶段(CD)。应变软化过后，充填体进入塑性状态，并且与理想塑性状态相近，屈服面始终不变。此时硬化模量A=0，根据式(8)可得理想塑形段的本构方程。

5 结论

(1)充填体单轴压缩实验表明，充填体强度与养护期龄、灰砂比、料浆浓度均正相关，灰砂比1∶6时，料浆浓度高于65%，灰砂比1∶8时，浓度高于72%，充填体的最终强度均可达到2.0～3.0 MPa，满足矿山充填要求。

(2)采用“定围压，加轴压”的方法进行的三轴压缩实验得到了充填体全应力－应变曲线，可分为初始压密阶段、线弹性阶段、非线性破坏阶段、应变软化阶段、塑性流动阶段5个阶段。

(3)相对峰值强度而言，充填体的残余强度对围压较敏感。在低围压(0.4 MPa)时，充填体试件脆性变形特征明显，围压增大致1.0 MPa时，充填体呈现出延性流动状态的趋势增强。因此，围压的增大可有效抑制充填体的破坏，在实际生产过程中应尽量减少充填体的暴露面积、暴露时间，以增加其抗压强度，同时，提高爆破工艺，避免充填死角的产生。

(4)建立了全尾砂充填体线弹－弹塑－塑性软化－理想塑性的本构模型。充填体峰后应变软化阶段可分为2种情况:在围压较小时，表现出明显应变软化，应力脆性跌落;在围压较高时，应变软化不明显，峰后直接进入塑性流动状态，残余强度与峰值强度差值减小。

(5)本研究采用的全尾砂胶结充填体均为实验室制备，条件较为理想，忽视了采场原位充填体强度与实验室强度的差异，需在充填采场进行现场取样，以便提出更为合理的设计安全系数。

［1］ 卢 平.制约胶结充填采矿法发展的若干充填体力学问题［J］.黄金，1994，15(7):18-22.

Lu Ping.A few points about themechanics of back filling which restrain the development of cementing back-fillingmethod［J］.Gold，1994，15(7):18-22.

［2］ 冯巨恩.金属矿深井充填系统的安全评价与失效控制方法研究［D］.长沙:中南大学，2005.

Feng Juen.Study on Safety Assessment and Failure Control Method of Deep-level Filling System in Metal Mine［D］.Changsha:Central South University，2005.

［3］ 刘同友.充填采矿技术与应用［M］.北京:冶金工业出版社，2001.

Liu Tongyou.Technology and Application of Mining Filling［M］.Beijing:Metallurgical Industry Press，2001.

［4］ 周爱民.矿山废料胶结充填［M］.北京:冶金工业出版社，2007.

Zhou Aimin.Waste Cementation Filling of Mine［M］.Beijing:Metallurgical Industry Press，2007.

［5］ 魏 微，高 谦，杨志强.全尾砂新型胶凝材料的现场力学试验［J］.金属矿山，2013(8):150-152.

WeiWei，Gao Qian，Yang Zhiqiang.Field mechanical experiment of neotype whole-tailings cementing materials［J］.Metal Mine，2013 (8):150-152.

［6］ 周保精，徐金海，倪海敏.小宽高比充填体沿空留巷稳定性研究［J］.煤炭学报，2010，35(S):33-37.

Zhou Baojing，Xu Jinhai，Ni Haimin.The small aspect ratio backfill gob-side entry retaining stability［J］.Journal of China Coal Society.2010，35(S):33-37.

［7］ 李一帆，张建明，邓 飞，等.深部采空区尾砂胶结充填体强度特性试验研究［J］.岩土力学，2005，26(6):865-868.

Li Yifan，Zhang Jianming，Deng Fei，et al.Experimental study on strength characteristics of tailings cement backfilling at deep-seated mined-out area［J］.Rock and Soil Mechanics，2005，26(6):865-868.

［8］ 刘志祥，李夕兵.尾砂胶结充填体力学试验及损伤研究［J］.金属矿山，2004(11):22-24.

Liu Zhixiang，LiXibing.Mechanics testand damage study on cemented tailing filling［J］.Metal Mine，2004(11):22-24.

［9］ 宋卫东，李豪风，雷远坤.程潮铁矿全尾砂胶结性能实验研究［J］.矿业研究与开发，2012，32(1):8-12.

Song Weidong，Li Haofeng，Lei Yuankun.Experimental research on the performance of cemented whole-tailings filling material in Chengchao Iiron Mine［J］.Mining Research and Development，2012，32(1):8-12.

［10］ 邓代强，高永涛，吴顺川，等.水泥尾砂充填体劈裂拉伸破坏的能量耗散特征［J］.北京科技大学学报，2009，31(2):144-148.

Deng Daiqiang，Gao Yongtao，Wu Shunchuan，et al.Destroy energy dissipation characteristics of cement-tailings backfill under splitting tensile condition［J］.Journal of Beijing University of Science andTechnology，2009，31(2):144-148.

［11］ 郭利杰，杨小聪.深部采场胶结充填体力学稳定性研究［J］.矿冶，2008，17(3):10-13.

Guo Lijie，Yang Xiaocong.Study onmechanics stability of cemented backfill formine stope［J］.Mining and Metallurgy，2008，17(3): 10-13.

［12］ 宋卫东，明世祥，王 欣，等.岩石压缩损伤破坏全过程试验研究［J］.岩石力学与工程学报，2010，29(S2):4180-4187.

SongWeidong，Ming Shixiang，Wang Xin，et al.Experimental study of rock compression-damage-failure process［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(S2):4180-4187.

［13］ 任建喜，葛修润.单轴压缩岩石损伤演化细观机理及其本构模型研究［J］.岩石力学与工程学报，2001，20(4):425-431.

Ren Jianxi，Ge Xiurun.Study of rock meso-damage evolution law and its constitutivemodel under uniaxial compression loading［J］.Chinese Journal of Rock Mechanics and Engineering，2001，20 (4):425-431.

［14］ 刘土光，张 涛.弹塑性力学基础理论［M］.武汉:华中科技大学出版社，2008.

Liu Tuguang，Zhang Tao.Basic Theory of Elasticity and Plasticity［M］.Wuhan:Huazhong University of Science and Technology Press，2008.

［15］ 陈明祥.弹塑性力学［M］.北京:科学出版社，2007.

Chen Mingxiang.Elasticity and Plasticity［M］.Beijing:Science Press，2007.