基于典型相关分析的地下停车场进出车辆数分析

刘 超， 刘 燕， 张凤荣， 阎慧臻， 张盛开

（大连工业大学 信息科学与工程学院，辽宁 大连 116034）

0 引 言

地下停车场是对地下空间的合理开发与利用的重要组成部分，尤其在市区的综合商业区，几乎无法单纯在地面解决停车问题。但在现实中，综合商业区附近人们往往无法在地面寻找到停车的地方，造成交通的堵塞，而相应的地下停车场却没有停满。由于地下停车场在扩大城市容量方面的优势和潜力，很多专家学者都对其进行了深入研究。王陈媛［1］提出了地下停车场系统布局面形态。祝华婷［2］运用排队论的方法建立模型用于确保停车场出入口的畅通运行。李红萍［3］基于DP网络的停车场设计为现代智能车库的管理提供了借鉴。以上的研究主要从设计的角度对地下停车场的现状进行了改进，并没有研究地下停车场进出车辆数的最值、均值等与时间的关系。两个数值型随机变量的相关性可用它们之间的相关系数度量。在许多实际问题中，需要研究两组随机变量之间的相关性。虽然相关系数可以了解变量间的相关性，但不能全面反映两组变量间的整体相关性，因此需要考虑构造各组变量的适当线性组合，将两组变量的相关性转化为有代表性的两个变量的相关性。本文采用典型相关分析的方法对地下停车场日均进出车辆数进行研究，提出了通过加强出入口管理以提升地下停车场利用效率的建议。

1 典型相关分析理论及推导

设x1，x2，…，xp表示实空间上的p个n维向量，其中xi＝ （xi1，xi2，…，xin）T，（i＝1，2，…，p）；y1，y2，…，yq表示实空间上的q个n维向量，其中yj＝ （yj1，yj2，…，yjn）T，（j＝1，2…q）。设 X ＝（x1，x2，…，xp）Tp×n，Y ＝ （y1，y2，…，yq）Tq×n是两组变量，令矩阵∑ 表示（XT，YT）T＝ （x1，…，xp，y1，…，yq）T的协方差矩阵，记为

再用（∑12）p×q＝ （σij）p×q表示X 与Y的协方差矩阵，其中σij表示xi与yj的协方差：

要研究X、Y两组变量之间的相关关系，作两组变量之间的线性组合，即

其中a＝ （a1，a2，…，ap）T，b＝ （b1，b2，…，bq）T为任意非零常向量，向量U，V的方差矩阵可表示为

由于对任意非负常数k1，k2有

问题归结为在约束条件（4）或（5）下，求a∈Rp，b∈Rq，使得

第一对典型相关变量，λ1为第一典型相关系数。

第一对典型相关变量U1，V1提取了原始变量X和Y之间相关的主要部分，如果这一部分还显得不够，则可以在剩余相关中再求出第二对典型相关变量，即满足约束条件（4）且不包括第一对典型相关变量所含信息的U2，V2。

2 应用分析

地下停车场是开发地下空间的重要组成部分［4－5］。本文选取的数据为大连市部分商业区地下停车场（福佳新天地地下停车场、家乐福三八店地下停车场、天兴罗斯福地下停车场、胜利广场地下停车场、和平广场地下停车场、期货大厦停车场和西安路家乐福地下停车场）每天的进出车辆数（数据来源于2013年12月《大连地下空间安全系统的研究与开发》）。为研究进入车辆数与离开车辆数的关系，选取如下变量：x1，每天单位时间进入车场车辆数最大值；x2，每天单位时间进入车场车辆数最小值；x3，每天进入车场车辆数的曲线积分值；y1，每天单位时间离开车场车辆数最大值；y2，每天单位时间离开车场车辆数最小值；y3，每天离开车场车辆数的曲线积分值。选取样本14个，对14组数据进行典型相关分析。

令X＝ （x1，x2，x3）T和Y ＝ （y1，y2，y3）T，经计算可得（XT，YT）T的相关系数矩阵

可得第一对典型变量的系数

通过公式（7）计算得第一对典型变量为

同理求得第二对典型变量系数a2，b2，代入公式（7）得第二对典型变量：

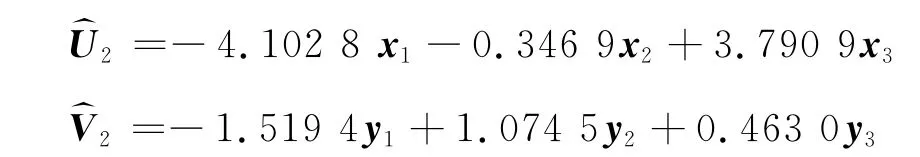
一般说来，典型变量的意义主要由那些系数绝对值较大的变量来决定［6－7］。在第一对典型变量中主要由日均进入车场车辆数控制，而主要由日均离开车场车辆数控制。因此，第一对典型变量主要反映了日均进入车场车辆数与日均离开车场车辆数的相关性；同理，第二对典型变量主要反映了每天单位时间内（小时）进入车场车辆数的最大值、日均进入车场车辆数的差异同离开车场车辆数的最大值、最小值的差异之间的相关性。

3 结 论

通过典型相关分析，可以将两组变量间的相关性凝结为少数几对典型变量间的相关性，通过对相关性较大的少数几对典型变量的研究来了解原来的两组变量相关性。地下停车场进出车辆数的典型相关性研究结果表明，日均进入车场车辆数与日均离开车场车辆数正相关；每天单位时间内（小时）进入车场车辆数的最大值与离开车场车辆数的最大值正相关、最小值负相关；日均进入车场车辆数与每天单位时间（小时）离开车场车辆数的最大值负相关、最小值正相关。

综合商业区地下停车场的日均进出车辆数最值与均值受时间的影响较大，因此商业广场地下停车场在日常管理中，应根据停车高峰的需求采取适当措施，比如在车辆短时间进入车场的增量值较多时，将出口临时变为入口，加快车辆进入车场的速度，减少拥堵；或在进入车场的车辆很少的时候，关闭一些停车场的出入口，减少运营管理成本。建议在以后修建地下停车场时预留可变更出入车道，即在进入车流量高峰时，将车道变为入口；而当离开车流量高峰时，将车道变为出口，这样可以按实际情况采取应变措施，缓解出入口车辆拥堵状况。

［1］王陈媛.地下停车场系统布局形态探讨［J］.地下空间与工程学报，2008，4（4）：615－619.

［2］祝华婷.大型专用停车库出入口数量与服务时间的计算方法［J］.湖南交通科技，2012，38（3）：149－153.

［3］李红萍.基于DP网络的地下停车场监控系统设计［J］.电气自动化，2013，35（6）：11－13.

［4］周健南.关于地下停车场建设的思考［J］.地下空间，2004，24（3）：370－372.

［5］张盛开，张亚东.现代物流管理与对策论［M］.大连：东北财经大学出版社，2010：2－7.

［6］刘冬.聚类分析和典型相关分析的应用举例［J］.赤峰学院学报：自然科学版，2011，27（6）：5－8.

［7］ZHANG Shengkai. Generalization of sequencing problems of the optimum service for model P－J［J］.Chinese Science Bulletin，1982，27（6）：594－597.