替代和置乱相结合的图像分块加密算法
2014-04-03
(内蒙古化工职业学院计算机与信息工程系,内蒙古 呼和浩特 010070)
0 引言
当图像在网络上传输时,对图像内容的有效加密和保护非常重要,保证信息的安全传输成为近年来学者研究的热点[1]。图像加密领域以图像置乱为主,可分成三类:像素位置变换方法[2-3]、像素值变换方法[4-5]以及两种方法相结合[6-11]的方法。
近年来,国内外学者提出众多加密方案。Fridich等人[12]提出一种基于二维标准baker映射的对称块加密技术;丁玮等人[13]提出按空间填充曲线、Arnold变换、幻方的图像置乱(置换)变换;文献[14]提出基于骑士巡游变换的图像置乱方法,实现了图像细节的隐藏;南艳红等人[15]探讨Fibonacci变换的置乱效果及其在数字图像水印中的应用[16],给出了一种描述数字图像置乱程度的定义,并比较Arnold变换和Fibonacci变换的置乱效果;邹建成等人[17]研究了Fibonacci变换在图像加密中的应用,取得了较好的加密效果;N.K.Pareek等人[18]结合两个Logistic混沌映射实现图像加密;Mazloom等人[19]基于非线性耦合混沌映射(CNCM)实现图像加密,通过对密钥做代数变换,有效地增强了加密系统的安全性;Sesha[10]和Vinod[20]将三维矩阵转换成为二维矩阵,顺序执行行列置换、行列替代、行列置换完成彩色图像加密;Pareek[21]利用像素替换和像素置换的方法,采用反馈机制增强系统鲁棒性。
本文基于二维Fibonacci变换和均匀分块的思想,提出了一种新的替代和置乱相结合的数字图像分块加密算法。该算法具有一定的抗剪切、抗噪声攻击的能力,而且实时性较好,可有效地对图像进行加密与解密。
1 图像置乱效果评价
图像置乱可以达到图像加密的目的,其目的是降低图像相邻像素相关性,使图像像素由确定性变为不确定性的过程,也就是使图像信息量增加的过程。用熵值来衡量置乱的效果,下面首先给出图像位置熵的定义:
(1)
式中:B为图像分块区域个数;Hk(P)为第k个分块区域的信息熵。
(2)
式中:P(i,j)为原始图像坐标为(i,j)的像素出现在置乱后图像的第k个图像块的概率。当P(i,j)等概率时,熵函数Hk(P)和位置熵H(R)最大。最佳的置乱状态是置乱后的图像中任意块内的像素点来自原始图像各个位置的概率相同,此时置乱后图像信源的平均信息量最大,熵值越接近于8,置乱效果越好。
均匀置乱是最好的置乱方法,它首先假设原始图像被分割成n×n块,每块含有n×n个点,且这些点分别出现在置乱后图像的n×n个图像块中。
2 本文加密算法
先将图像做分块处理,正方块在图像加密的研究中具有代表意义。假设图像的尺寸为M×N,以f(i,j)(1≤i≤M,1≤j≤N)为中心的m×n(0≤m≤M,0≤n≤N)个相邻像素组成的邻域,称为图像块,且约束条件如下:①图像行列数为2的指数;②每个图像块的行列数相等。对16×16的图像均匀分块,将该图像分成8×8块,每块含有2×2个像素点,其示意图如图1所示。
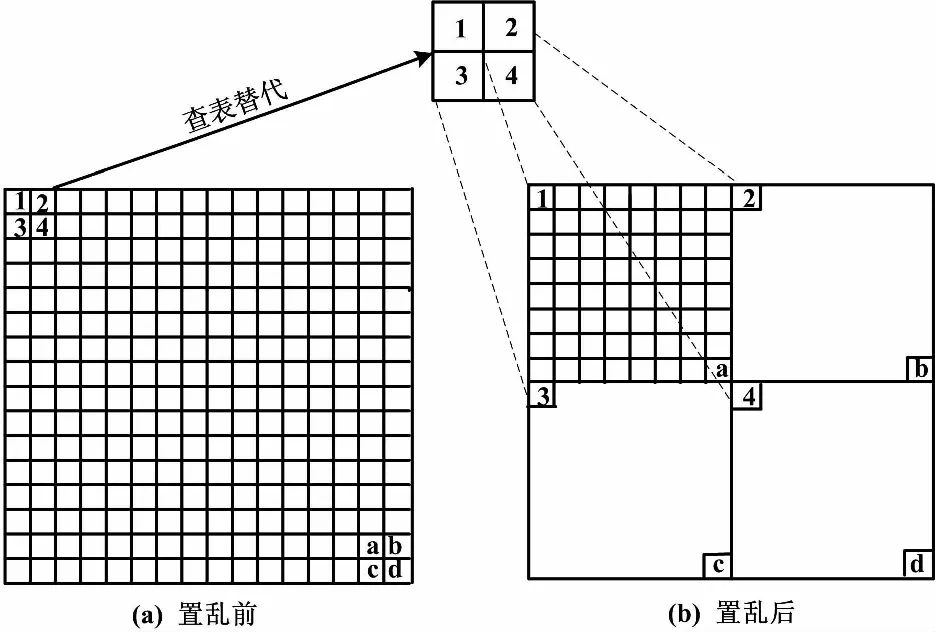
图1 图像块内像素值替代和均匀分块示意图
加密算法具体步骤如下。
① 将图像分成8×8块(记作P1,P2,…,P64),每块含有2×2个像素点(记作p1,p2,p3,p4),假设图像灰度级是256,即8位(b1b2…b8)二进制构成每个像素点,根据前一像素点pi-1的三个最重要位(b1b2b3)的值和如表1所示的该位值的操作,修改pi的像素值。例如,首先取出P1块,p1和p2的像素值分别是201(11001001)和185(10111001)。像素点p1相应的位值6(110)进行查表,对p2的像素值循环左移一位后取反,由新像素值141(10001101)替代185(10111001)。根据p2新像素值修改p3的像素值,同理修改p4的像素值,并根据该值修改p1的像素值。按照以上规律,依次完成块P1,P2,…,P64的替代操作。

表1 位值和相应的操作
② 对步骤①得到的图像块进行如下操作:根据前一像素点pi-1的两个最重要位(b1b2)的值和表1对应该位值的操作,修改pi的像素值。例如,p3和p4的像素值分别是140(10001100)和186(10111010),则对p4应用p3相应的位值2(10)进行运算,采用新值69(01000101)替代p4的原像素值。按照以上规律,依次实现块P1,P2,…,P64的替代操作。
③ 对步骤②得到的图像块进行如下操作:根据前一像素点pi-1的最重要位(b1)的值和表1对应该位值的操作,修改pi的像素值。例如,p2和p3的像素值分别是235(11101011)和153(10011001),则p3的像素值应用p2相应的位值1(1)进行运算后变成76(01001100)。按照以上规律,依次对块P1,P2,…,P64完成替代操作。
④ 完成上述步骤后,采用均匀分块算法将每个图像块内的所有像素充分扩散到其他图像块中。如图1所示,实现原始图像各块中像素点间的距离由“最近”到“最远”,保证该块中所有像素点被分到置乱后图像的不同块中,满足条件S≥P;实现原始图像各块中像素点间的距离由“最远”到“最近”,按照规定的次序,在原始图像所有块中各取一点,同时分到置乱后图像的同一块中,满足条件S≥p。因为s≥P、S≥p,则sS≥PS≥pP,已知sS=pP,那么s=P、p=S。置乱后图像分成2×2(S×S)块,每块含有8×8(s×s)个点。
⑤ 分别对置乱后的每个图像块做Fibonacci像素值置乱,h表示任意像素值横纵坐标的十六进制,分别取出每个像素高4位和低4位作为Fibonacci变换的输入,Fibonacci像素值置乱表示形式如下:
(3)

⑥ 对整幅图像做位置变换,将置乱后的整幅图像作为Fibonacci位置变换的输入,利用以下公式进行变换。图像像素的位置矩阵表示为p=[x,y]H,则对图像做n次Fibonacci位置变换表达式为:
(4)
式中:x,y,x′,y′∈{0,1,…,N-1};整数N≥2为数字图像矩阵的阶数;(x,y)和(x′,y′)分别为原图像和变换后图像像素的行位置和列位置坐标。
图像加密流程如图2所示。

图2 图像加密流程图
3 试验效果与分析
3.1 置乱效果比较
从美国南加州大学USI-SIPI image database和美国麻省media实验室图像库中选择实验图像。通过对大量图像进行试验分析,均得到了一致的结果。本试验选择典型的Lena图像,文献[22]和本文算法的分块示意图如图3所示。

图3 图像分块示意图
图3(a)~图3(d)所示为采用文献[22]提出的高效率分块图像置乱算法得到的分块示意图,该算法分两步进行:首先对图像分块;然后对图像块进行Arnold变换。图3(e)~图3(h)为采用本文算法由不同分块数目获得的加密效果。加密图像所对应的灰度直方图如图4所示。直观上看本文算法置乱效果更均匀,既改变了图像的纹理信息又改变了统计信息,达到了混乱和扩散的效果,加密图像的直方图的均匀分布也说明了这一点。
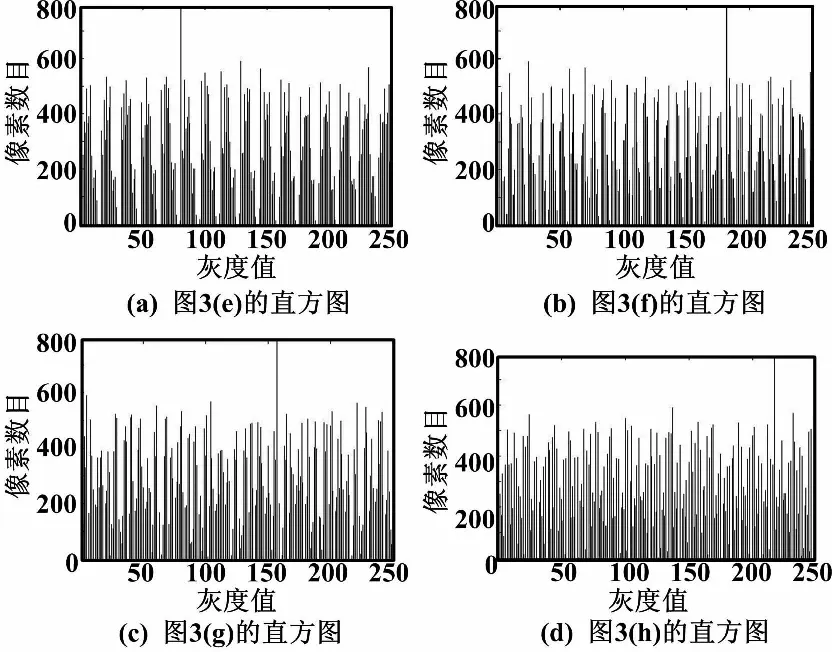
图4 加密图像灰度直方图
从直观上比较两种算法的置乱效果欠缺说服力,本文引入置乱度(SM)来衡量图像的置乱性能,它能较好地反映图像的置乱程度[23]。SM的计算式为:
(5)
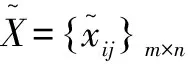
为了衡量图像分块数对本算法的影响,分别采用不同的分块数对原始图像进行加密,试验结果如表2所示。

表2 分块数对置乱度的影响
从表2可以看出,两种算法的置乱度随分块数的增加呈非线性递增趋势,而本文方法置乱度增加缓慢,说明该算法的置乱程度受分块数影响较小,算法有效。
3.2 相邻像素相关性分析
图像的本质特征决定了图像中相邻像素间具有较强的相关性。基于这一性质,利用统计攻击方法来分析图像加密算法具有较高的可行性,因此用相关系数来衡量加密算法破坏相邻像素相关性的能力。
(6)
(7)
(8)
(9)
式中:x和y分别为相邻两个像素的像素值;E(·)、D(·)和Cov(·,·)分别为期望、方差和协方差;r为相邻两像素的相关系数,r的值接近1的程度越高,则图像相邻像素的相关性越强。
分别采用Arnold-Fibonacci变换(即A-F变换)、文献[22]算法和本文算法对Lena图像进行加密,从图像中随机选取1 000对相邻像素点(水平、垂直和对角),然后利用以上公式分别计算图像在三个方向的相邻像素相关系数,其结果如表3所示。由表3可知,原始图像的相邻像素高度相关,本文算法去相关性能力较强,加密图像的像素相关性接近于0,且熵值更接近8,可见本文加密算法优于其他算法。
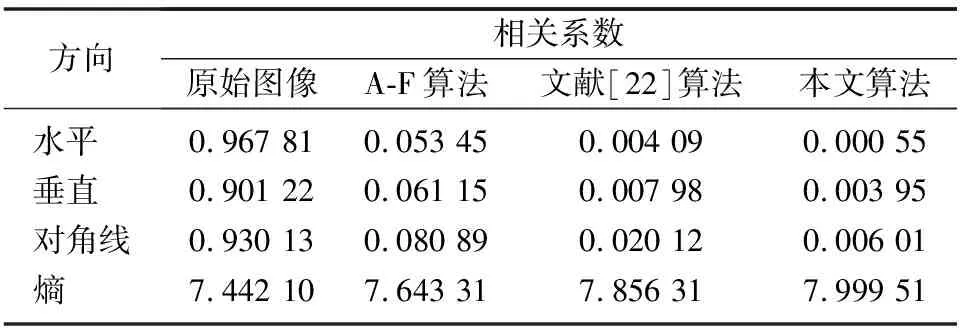
表3 相邻像素的相关系数对比
3.3 抗剪切性能
数字图像经常发生剪切攻击,如果图像受到不同程度上的剪切,算法仍然能够在一定程度上恢复原始信息,则说明该加密解密算法对剪切具有鲁棒性。首先利用本文算法对Lena图像进行加密,然后进行一定程度的剪切,最后对剪切图像进行解密,如图5所示。

图5 抗剪切试验结果图
由图5可以看出,即使图像受到50%的剪切,解密算法仍然能够恢复出原始图像,说明本算法是有效的,可抗剪切攻击。本文加密算法具有均匀置乱步骤,保证了被剪切掉的部分具有最大的不相关性,同时加密后的图像具有最大的不相关性,从而可以很容易地恢复原始图像。
3.4 抗噪声试验
为了验证本文算法的抗噪声性能,在加密后的图像中加入均值为0、方差为σ的高斯白噪声。在图3(h)中加入不同方差的高斯噪声然后采用本文算法进行加密与解密,抗噪声试验结果如图6所示。

图6 抗噪声试验结果图
通过上述噪声攻击试验可以看出,当加密图像受到不同程度的高斯白噪声影响时,本文的解密算法也能基本恢复原始图像,而且基本不会影响图像整体视觉效果,表明本算法可以抵抗不同程度的高斯白噪声攻击。
3.5 执行速度分析
试验运行平台为Pentium(R)、双CPU、2.10 GHz、内存2 GB的计算机,操作系统为Windows XP企业版,利用VC++6.0编写相应的加密、解密算法,并记录执行时间,对文献[22]、文献[24]、文献[25]算法进行了对比,得到的执行时间如表4所示。由表4可知,本文算法远优于文献[24],文献[24]与文献[22]的执行时间相差不到1 s。
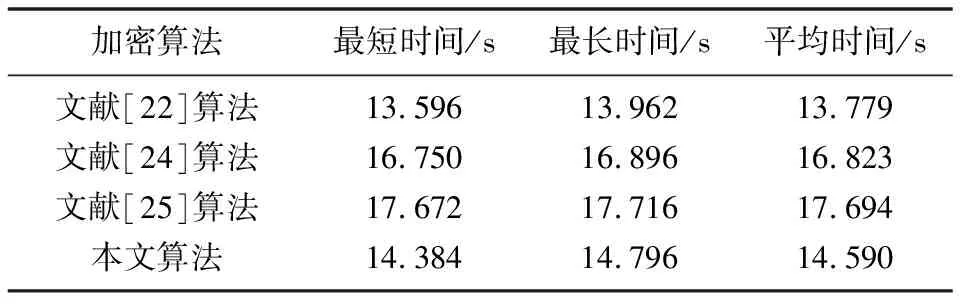
表4 不同算法的执行时间
4 结束语
本文基于二维Fibonacci变换和均匀分块的思想,提出了一种新的图像分块加密算法[25-27]。首先对原图像分块,对块内像素点执行按位替代操作,然后利用均匀分块算法置乱,再对置乱后的每个图像块进行Fibonacci像素值置乱,最后对块置乱后的图像进行Fibonacci位置置乱。试验表明,本文算法加密、解密效果较好,可以抵抗不同程度的剪切、噪声等常规攻击,而且算法具有一定的实时性,满足实际应用。
[1] 齐东旭,邹建成,韩效宥.一类新的置乱变换及其在图像信息隐蔽中的应用[J].中国科学(E辑),2000,43(3):304-312.
[2] Won Y,Hyoungshick K.An image encryption scheme with a pseudorandom permutation based on chaotic maps[J].Communication in Nonlinear Science and Numerical Simulation,2010,15(12):3998-4006.
[3] NayakC K,Acharya A K,Das S.Image encryption using an enhanced block based transformation algorithm[J].International Journal of Research and Review in Computer Science,2011,2(2):275-279.
[4] Ismail I A,Amin M,Diab H.A digital image encryption algorithm based a composition of two chaotic logistic map[J].International Journal of Network Security,2010,11(1):1-10.
[5] Chen Dongming,Chang Yunpeng.A novel image encryption algorithm based on logistic maps[J].Advances in Information Science and Service Sciences,2011,3(7):364-372.
[6] Pareek N K,Patidar V,Sud K K.Image encryption using chaotic logistic map[J].Image and Vision Computing,2006(24):926-934.
[7] Patidar V,Sud K K.Modified substitution-diffusion image cipher using chaotic standard and logistic maps[J].Communication in Nonlinear Science and Numerical Simulation,2010(15):2755-2765.
[8] Jolfaei A,Mirghadri A.Image encryption using chaos and block cipher[J].Computer and Information Science,2011,4(1):172-185.
[9] Sathishkumar G A,Bagan K B.A novel image encryption algorithm using pixel shuffling base 64 encoding based chaotic block cipher[J].WSEAS Transactions on Computers,2011,10(6):169-178.
[10]Indrakanti S P,Avadhani P S.Permutation based image encryption technique[J].International Journal of Computer Applications,2011,28(8):45-47.
[11]Patidar V,Pareek N K,Purohit G.A robust and secure chaotic standard map based pseudorandom permutation-substitution scheme for image encryption[J].Optics Communications,2011(284):4331-4339.
[12]Fridrich J.Symmetric ciphers based on two-dimensional chaotic maps[J].Internation Journal of Bifurcat Chaos,1988,8(6):1259-1284.
[13]丁玮,齐东旭.数字图像变换及信息隐藏与伪装技术[J].计算机学报,1998,21(9):839-843.
[14]柏森,曹长修,曹龙汉.基于骑士巡游变换的图像细节隐藏技术[J].中国图像图形学报,2001,6A(11):1096-1100.
[15]南艳红,李南,邹建成.Fibonacci变换及其在数字图像水印中的应用[J].中山大学学报:自然科学版,2004,43(2):148-151.
[16]Zou J C,Qi D X,Rabab K.A novel watermarking method based on Fibonacci numbers[C]//Proceedings of ACM International Conference on Virtual Reality Continuum and its Applications,2006:335-338.
[17]Zou J C,Rabab K W,Qi D X.A new digital image scrambling method based on fibonacci numbers[C]//Proceedings of the 2004 IEEE International Symposium on Circuits and Systems,2004:965-968.
[18]Pareek N K,Patidar V,Sud K K.Image encryption using chaotic logistic map[J].Image and Vision Computing,2006(24):926-934.
[19]Mazloom S,Eftekhari A M.Color image encryption algorithm based on coupled nonlinear chaotic map[J].Chaos,Solitons & Fractals,2009,42(3):1745-1754.
[20]Patidar V,Purohit G,Sud K K.Image encryption through a novel permutation-substitution scheme based on chaotic standard map[C]//International Workshop on Chaos-Fractals Theories and Applications,2010,5(8):164-169.
[21]Pareek N K.Design and analysis of a novel digital image encryption scheme[C]//International Journal of Network Security & its Applications,2012,4(2):95-108.
[22]王圆妹,李涛.基于Arnold变换的高效率分块图像置乱算法的研究[J].电视技术,2012,36(3):17-19.
[23]侯启槟,杨小帆,王阳生等.一种基于小波变换和骑士巡游的图像置乱算法[J].计算机研究与发展,2004,41(2):369-375.
[24]王道顺,杨地莲,齐东旭.数字图像的两类非线性变换及其周期性[J].计算机辅助设计与图形学报,2001,13(9):829-833.
[25]Zou J C,Rabab K W,Qi D X.The generalized fibonacci transformations and application to image scrambling[C]//Proceedings of the 2004 IEEE International Conference on Acoustic,Speech,and Signal Processing(ICASSP),2004:385-388.
[26]李太勇,贾华丁,吴江.基于三维混沌序列的数字图像加密算法[J].计算机应用,2006(7):52-56.
[27]向德生,熊岳山.基于约瑟夫遍历的数字图像置乱算法[J].计算机工程与应用,2005(10):23-24.
