LLSTA和ELM算法在转子故障诊断中的应用
2014-04-03
(东北电力大学能源与动力工程学院,吉林 吉林 132012)
0 引言
现代汽轮机转子的结构越来越复杂,出现故障的原因也日趋多样性,这给设备的故障诊断带来了困难[1-2]。汽轮机转子的故障诊断过程大体可以分为3个步骤:①故障信号的采集及处理;②故障特征的提取;③模式识别。其中特征提取是故障诊断的关键步骤。因而寻找一种有效可行的故障特征提取方法对于顺利进行故障模式识别分类和完成设备的故障诊断具有重要的意义和价值。
针对高维非线性的故障数据空间,利用线性局部切空间排列(linear local tangent space alignment,LLTSA算法对数据进行特征提取[3-4],数据降维前后的内在属性没有任何变化。LLTSA算法保持了非线性流形结构的低维内在本质特征,比传统的流形学习算法具有更好的分类识别能力[5-6]。
极限学习机(extreme learning machine,ELM)是近年来由Huang G B提出的一种单隐含层前向反馈神经网络(single-hidden layer feed-forward neural network,SLFN)分类器[7-10],这种分类器相对于BP神经网络(BP neural network,BPNN)、支持向量机(support vector machine,SVM)等分类器[11-12],不仅具有良好的泛化性,也极大地提高了前向神经网络的学习速度和效率。本文采用了“故障信号-时域与频域的融合-LLTSA-ELM”的诊断模型,该模型实现了故障诊断的全程自动化、快速化和准确化。
1 LLTSA和ELM原理
1.1 线性局部切空间排列算法
LLTSA是在LTSA的基础上发展起来的,算法增加了主成分分析(principal component analysis,PCA)过程,通过无限靠近每一样本点的空间来构建低维的线性局部空间,然后利用局部切空间排列求出整体低维嵌入坐标。
故障样本个数为n,故障样本维数为m,XORG为含噪声故障样本集,LLTSA算法的目的是找到高维样本集XORG在Rd空间的数据集Y,其表达式为:
Y=ATXORGGn
(1)
式中:Gn=E-iiT/n为中心矩阵,E为单位矩阵,i为所有元素为1的n维列向量;Y为XORG潜在的d维非线性流形。
线性局部切空间排列算法步骤如下。
② 计算邻域。通过K-近邻(KNN)方法搜寻数据点xi的邻域,首先应用欧几里得原理得出所有数据点的距离矩阵,再通过分析距离矩阵寻找数据点xi的k个同类近似点xj。
③ 获取局部信息。计算XiGk(其中,Xi=[xi1,…,xik])的d个最大特征值对应d个特征矢量构成的矩阵Fi,Gk=E-iiT/k。
④ 排列矩阵的构造。
通过局部累加构造矩阵A为:
(2)

⑤ 映射的计算。
XGnAGnXTβ=λXGnXTβ
(3)
与特征值λ1,λ2,…,λd(λ1<λ2<…<λd)对应的特征解为β1,β2,…,βd,则BLLTSA=[β1,β2,…,βd]。转换矩阵B=BPCA×BLLTSA,则X→Y=BTXORGGn
1.2 极限学习机方法的基本原理与算法
对于N个不同的训练样本,其集合表示为N={(Xi,Yi)|i=1,2,…,N;Xi∈Rn;Yi∈Rm},具有隐藏节点数M且激活函数为f(x)的SLFN模型为:
(4)
式中:αi为连接第i个隐藏层节点的输出权值;βi为连接第i隐藏层节点的输入权值;bi为第i个隐藏节点的偏置;oj为第j个样本的输出值。
假设标准单隐层前馈神经网络能够零误差逼近N个样本,即:
(5)
由αi、βi、bi可得:
(6)
Gα=T
(7)
式中:G为神经网络的隐层输出矩阵。
G中的第i列定义为第i个隐层节点对应的输入X1,X2,…,XN的输出向量,其表达式为:
(8)
输出权值可通过最小范数的最小二乘解来获得,即:
α=G+T
(9)
式中:G+为隐层输出矩阵G的Moore-Penrose广义逆。
极限学习机的基本思路是:网络参数并不需要全部进行设定,输入权值β和隐含层节点偏置值b在计算过程中可随机给定,这大大提高了收敛速度。通过式(9)使输出权值得到了最小的训练误差,自身的最小范数也得到了最优的泛化性能,最终计算结果使得范数的最小二乘解是唯一的,从而使算法不会产生局部最优解。
2 故障诊断实例分析
2.1 试验数据的采集
转子振动试验台可以模拟振动信号,通过人为措施制造一些故障来模拟汽轮机转子的振动故障。试验装置包括转子ZXP- 4A、振动试验台、数字测振仪主机、信号采集器、电涡流传感器、计算机以及信号处理器DASP等。模拟的故障分为3类,包括不对中、不对中加松动、转子质量不平衡。各种故障模拟的方法具体如下:不对中故障是将联轴器换成硬质橡胶管,并在轴末端的轴承座底垫上1~2个垫片,人为地将轴承座扭转一定角度实现;不对中加松动故障则是在不对中的试验中同时加入轴承座松动来实现;不平衡故障通过在临近电涡流传感器的转子转盘上旋入3~5个螺丝钉。
故障信号的原始振动频率为1 000 Hz,采取样本点数为8 000点,试验中,3种转子转速分别为1 000 r/min、1 150 r/min和1 200 r/min。在每个转速下,每种故障采取10组样本数据。
2.2 构造高维特征空间
故障诊断过程中,为了全面刻画转子系统不同类型的故障特性,本文将采用混合域特征融合方法(时域和频域的融合)来描述转子不同故障的信息,从而解决汽轮机故障诊断方法的通用性问题。从样本信号中选取11个时域特征和3个频域特征来构造14维特征空间,用绝对均值、均方根值、方根幅值、歪度、峰值指标、裕度指标、峭度指标、最大峰值、方差、峭度、脉冲指标代表11个时域参数,将平均频率、谱峰稳定指数、相对功率谱能量作为频域统计指标。在试验数据中,截取长度为t的振动信号,利用相空间重构方法将数据划分为N个子数据量,然后再分别算出每个子数据量的14维特征值,这样就构造了N×14的高维特征矩阵,N代表样本点数,高维特征空间包括了14种描述机械振动特性的特征参数。
2.3 数据降维仿真过程
3种降维方法的特征分布图如图1所示。
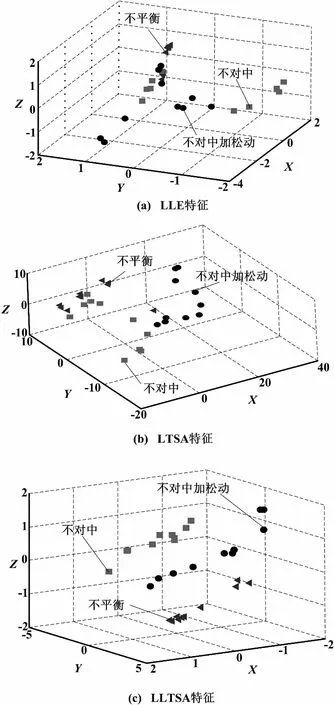
图1 3种降维方法的特征分布图
分别用LLE、LTSA、LLTSA对高维矩阵X降维,得到低维空间Y,然后投影到可视空间来完成视觉故障分类。设定近邻点数K=15,投影维数d=3。在分析过程中,LLE的分类效果最差,3种故障样本有交叠的部分,而且不同故障的类型距离也非常近,不能区分故障。LTSA的分类效果相对于LLE要好一些,但是不对中和不平衡故障样本也有交叠的部分,不同故障类型距离也较近,不太容易进行故障分类。LLTSA效果较好,不同故障点没有交叠的部分,而且也相对距离较远,容易分辨不同类型的故障。
为了进一步说明LLTSA的性能,每类故障选用160个训练样本,80个测试样本,选用支持向量机作为分类器对结果进行分析、通过反复试验,确定高斯函数为核函数,确定核半径σ=0.99和误差惩罚参数λ=100为最优参数,计算机配置为Core(TM)2,CPU 2.20 Hz,内存2 GHz。不同特征提取方法比较如表1所示。从表1可以看出,每种方法的样本训练时间和测试时间相差不大,但是LLTSA与SVM构造的故障分类器训练准确率和测试准确率最高,充分体现了LLTSA具有较高的综合性能。
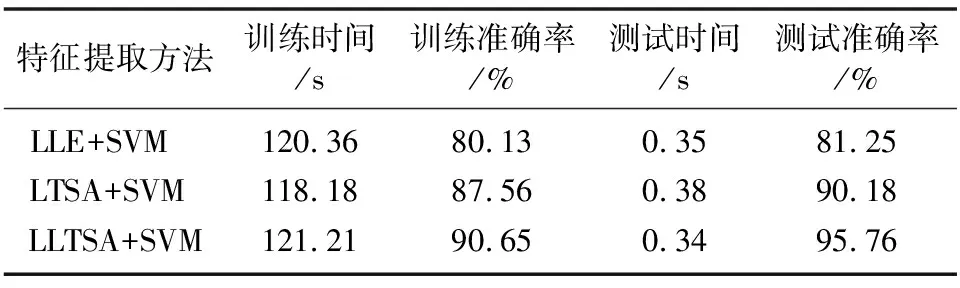
表1 不同特征提取方法比较
2.4 ELM诊断结果分析
本文以20作为初始化隐藏节点个数,然后以5为单位依次递加,选取Sin、Sigmoidal、Radial basis作为激活函数进行试验。测试准确率变化曲线如图2所示。

图2 测试准确率变化曲线
从图2可以看出,随着隐藏节点数的增加,各种激活函数的测试准确率也随之增加,增加到一定程度后都保持稳定。经综合考虑,我们确定Sin函数为ELM的激活函数,最优隐藏节点数确定为70。BP网络模型选用运算速度最快、最稳健的Levenberg-Marquardt 算法,确定最佳隐藏节点数为130。每类故障依然选用160个训练样本和80个测试样本。
不同诊断模型比较如表2所示。
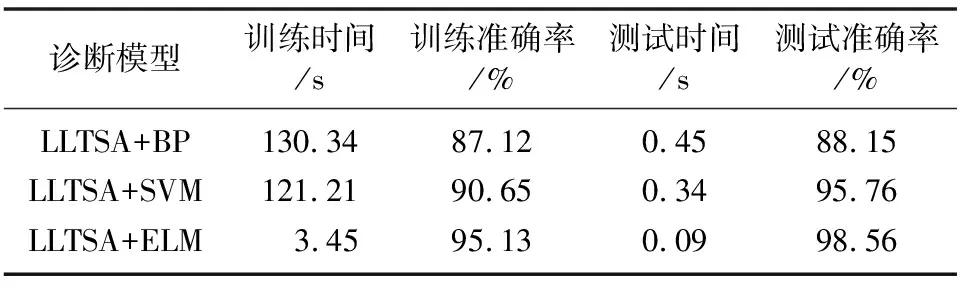
表2 不同诊断模型比较
从表2可以看出,在训练速度方面,由于ELM自动调整网络的输入权值以及隐元的偏置,LLTSA和ELM构造的故障分类器所用的训练时间非常短;而SVM和BP网络的训练过程需要反复迭代来确定参数,所以耗时较长;ELM的测试速度也要好于其他两者,训练和测试准确率也非常高,说明该模型的泛化能力更好。
3 结束语
本文将流形学习方法应用到转子故障诊断中,提出了一种有效的线性局部切空间排列算法(LLTSA)。将LLTSA的维数化简效果与LTSA、LLE作对比,表明了LLTSA算法成功提取了高维非线性数据的低维流形的特征,明显改善了故障模式识别的分类效果。这3种流形算法维数化简后的故障诊断精度表明,无论是在提取低维流形特征方面,还是在故障诊断率方面,LLTSA的分类性能都优于LTSA、LLE。
不同的激活函数会影响ELM的性能,本文使用了Sin、Sigmoidal、Radial basis作为激活函数进行试验,说明了Sin函数和其他激活函数相比,具有更好的测试分类效果。通过LLTSA+ELM和其他两种故障诊断模型对比,充分证明了ELM在训练速度、测试速度、准确率方面的优越性。
[1] 简小刚,张艳伟,冯跃,等.工程机械故障诊断技术的研究现状与发展趋势[J].中国工程机械学报,2005,3(4):446-449.
[2] 程加堂,艾莉,徐绍坤.汽轮机转子故障诊断中的应用[J].自动化仪表,2012,33(11):13-14.
[3] Seung H S,Daniel D L.The manifold ways of perception[J].Science,2000,29(55):2268-2269.
[4] Kouropteva O,Okun O,Pietikainen M.Supervised locally linear embedding algorithm for pattern recognition[J].Pattern Recognition and Image Analysis,2003,26(9):386-394.
[5] Liu X M,Yin J W,Feng Z L,et al.Orthogonal neighborhood preserving embedding for face recognition[C]//2007 IEEE International Conference on Image Processing,New York,USA:IEEE,2007:133-136.
[6] 薛广鑫,陈军,蒋能飞.基于局部线性嵌入和云神经网络的转子故障诊断方法[J].振动与冲击,2012,31(23):100-103.
[7] Huang G B,Babri H A.Upper bounds on the number of hidden neurons in feed forward networks with arbitrary bounded nonlinear activation functions[J].IEEE Transaction on Neural Networks,1998,9(1):224-229.
[8] Law Y W,Etalle S,Hartel P H.Key Management with group-wise pre-deployed keying and secret sharing pre-de-ployed keying[R].Technical Report TR-CTIT- 02-25,University of Twente,2002.
[9] Eschenauer L,Gligor V D.A Key management scheme for distributed sensor networks[C]//Proceeding of ACM Conference on Computer and Communication Security,2002:41-47.
[10]常玉清,李玉朝,王福利.基于极限学习机的生化过程软测量建模[J].系统仿真学报,2007,19(23):5587-5590.
[11]万鹏,王红军,徐小力.局部切空间排列和支持向量机的故障诊断模型[J].仪器仪表学报,2012,33(12):2790-2795.
[12]王忠峰,汤伟,黄俊梅.BP神经网络在轴承故障诊断中的研究与应用[J].化工自动化仪表,2010,38(3):327-331.
