基于马尔科夫的多路控制器可靠性及安全评估
2014-04-03
(陕西科技大学电气与信息工程学院,陕西 西安 710021)
0 引言
工业控制系统是自动化技术、计算机技术、网络通信技术和传感器技术相结合的产物,已被广泛应用于诸如石油、化工、电力、冶金等各种工业生产领域。随着工业控制系统的不断完善,工业控制器随之不断发展,但同时也面临着一系列新的挑战和问题。
工业控制器作为工业控制系统的核心部件,它的可靠性直接决定了整个控制系统的稳定、可靠和安全。由于工业控制器的软硬件随机失效导致的系统失效以及维护过程中因误操作造成的设备故障,给工业生产现场造成了严重的生产事故,高温、高压、易燃易爆等因素还会造成严重的人身伤害和财产损失。如何有效提升工业控制器的可靠性已经成为工业控制系统设计中的关键问题。
自动控制系统的安全性和可靠性已成为衡量系统是否完善的重要指标。一个安全可靠的控制系统所带来的经济效益不仅体现在减少停机时间、提高产品质量、减少维修成本、降低投资风险等方面,还体现在维修的调度性等。因此,本文以多路控制器为对象,建立马尔科夫模型。该模型为该控制器及系统的维修与测试提供了有效的依据[1]。
1 多路控制器的特点
本文安全评估的对象是以嵌入式系统为基础,以ARM为内核的远程且通用的多路控制器,在控制过程中,运用典型的PID算法,对被控参数进行调节。多路控制器具有实时记录数据和报错预警的功能。
多路控制器的主要特点有:①能实现友好、操作便捷的用户图形界面;②能实现控制器的实时性、快速性和准确性;③加入扩展接口,方便用户根据需求对内存的扩展;④运用以太网通信电路,能实现控制器的通信能力;⑤在输入输出上能实现通用的多路控制[2-4]。
多路控制器应使用不同参数的传感器去测量和获取模拟量。例如运用最常见的温度传感器来测量获取被控对象的温度参数。本文后续将以测量温度参数为例,对该控制器系统建立马尔可夫模型,并对其安全性和可靠性进行评估[5]。
2 安全与可靠性评估
现如今,工业控制器的功能越来越复杂,性能也越来越高,同时对微处理器和存储器等复杂电子器件的依赖程度也越来越强,多数工业控制器都是复杂电子系统,属于软硬件相结合的电子系统。这类电子系统的一个特点是存在较为复杂的硬件随机失效。这种随机失效可能是由于电子器件引起的,也可能是由于生产过程所造成的,它的出现会导致工业控制器的控制功能受到严重影响甚至失效,从而影响系统整体功能和性能,甚至影响生产安全。
除了硬件随机失效可能导致的工业控制器故障之外,由于复杂功能和高性能设计所带来的其他类型的不可避免的系统失效,也必须考虑到工业控制器的可靠性和安全性设计中。所谓的系统失效是由于设计及实现上的缺陷和考虑不周所导致的,例如硬件设计缺陷、软件机制漏洞或程序缺陷。虽然系统失效理论上能够通过严格的开发设计流程和设计实现经验来消除,但在实际工业控制系统中是不可能做到100%消除的。因此,如果得到某系统的稳态可用率或计算出一个系统处于失效状态的平均概率,就可依照获得的数据来提高设备或系统的安全性、可靠性[6]。
2.1 软硬件失效
多路控制器系统的失效可分为三种,一种是由硬件造成的,称之为硬件失效;第二种是由软件造成的,称之为软件失效;最后一种为人为失效[6]。软件失效不同于其他类型的系统失效,该失效是软件设计人员在不经意间“设计”到系统的。由于软件本身不会磨损,因此不存在不能被发现的重复性错误,也不存在潜在的制造缺陷。这种情况使得部分人认为软件失效不能通过统计的方法来进行建模。他们认为系统完全是确定性的,而不是随机的。这种观点是正确的,但是却忽略了计算机实际运行情况。实际上,输入序列的数目是非常巨大的,并且是符合统计原理的。我们发现,当有大量输入序列“进入”系统时,有些系统将会发生故障[7]。
综上所述,对软件失效举例说明。工程师将新的控制逻辑装入PLC,系统安装了模拟量输入模件。输入该模拟量模件的正常信号是由电位器给定的1~4 V的信号,电位器是用来测量机械位移的。启动时,系统运行正常,所有其他的测试也都全部通过。几个月后,该机械不能正常停止,电位器的电刷超出了它的正常使用范围,PLC停止工作。即PLC软件发生故障,失效信息定义为“除以0”。
在工业控制过程中,对于硬件失效即物理(随机)失效,举一简单例子说明。由单板控制器模件构成的系统,如果发展故障,则控制器输出中断并且不再给电磁阀提供电流,在这种情况下,通过控制器诊断,发现了一个失效的输出晶体管部件。将输出晶体管拆开,检查后发现它不能导通,即晶体管发生开路故障而导致系统不能正常工作,这种系统失效叫做硬件失效[7]。
硬件失效和软件失效对于控制系统安全性和可靠性的分析都具有重要性。我们需要通过失效信息来帮助决策如何避免发生失效或在失效前给予维修。
对于前文所述的软件失效,其失效分析如表1所示。

表1 软件失效分析表
在工业领域,大多数系统都是可维修系统。维修就需要花时间,简单的可靠性网络建模方法不能直接计算维修时间。概率方法可以提供维修时间的近似解,但是它只能在低失效率和短维修时间的条件下才能获得误差比较小的结果。对于失效率和维修时间大范围变化的情形,对可维修系统失效性能的建模需要采用另外一种方法,即建立马尔科夫模型[8]。这种方法必须考虑实际的维修时间、不同的系统配置等因素。
2.2 马尔科夫模型
马尔可夫模型是一种通过采用状态图,对可靠性和安全性进行建模的方法[8],其状态图仅使用两个简单的符号。虽然图形简单,但与其他的可靠性和安全性评估技术相比,马尔科夫模型提供了一套完整的评估工具。马尔可夫模型中的基本符号如图1所示。

图1 马尔可夫模型符号
图1(a)表示正常的工作部件与发生失效的部件组合状态符号,图1(b)表示由一种状态向另一种状态转换。模型特点是多数失效模式可以表示在一幅图上。
马尔可夫模型可以在一幅图上表示容错系统的各种工作状态,其示意图如图2所示。如果模型建立得很完整,那么它将表达系统的全部正常状态。同时马尔可夫模型也表示系统的各种降级状态,此时系统还可以正常工作,但是不能再进一步失效了。

图2 马尔可夫模型工作状态示意图
图2中,λi表示部件的瞬时失效率,即部件由一个状态转移到下一个状态的失效转换;μi表示维修率。
2.3 求解马尔可夫模型
马尔可夫建模技术包括:定义系统中全部成功/失效状态。这些状态由带有编号的圆来表示。系统由一种状态向另一状态转换,状态之间的转换用箭头转移弧表示,并标注相关的失效率[6]。如对于单个不可维修部件来说,有0和1这2个状态,在状态0,部件正常工作;在状态1,部件发生失效,失效率为λ。单个不可维修部件模型如图3所示。

图3 单个不可维修部件模型
本文以多路控制器为对象,以控制温度过程中监测被控对象的温度参数为例,条件为:每10 min测量一次温度,测量100次则会产生一次失效,平均维修时间为20 min。该过程适合于马尔可夫离散时间模型,时间间隔选为10 min,一共需要2个状态,状态0表示正常工作,状态1表示失效。系统起始于状态0,即正常工作状态。由状态0开始,系统在每个时间间隔内有2种状态:稳定在状态0或移动至状态1。系统有1%的概率由状态0转移到状态1。对于每个时间间隔,系统不是移动到新的状态就是停留在当前的状态,这2种概率和为1,因此,系统停留在状态0的概率是99%(1-0.01=0.99)。一旦系统失效,那么系统则可能停留在状态1(还没有修好),或移动到状态0(已经修好),因此,在任何时间间隔内,由状态1移动到状态0的概率为0.5(10 min时间间隔、20 min维修时间),则系统停留在状态1的概率即为1-0.5=0.5。马尔可夫模型如图4所示。
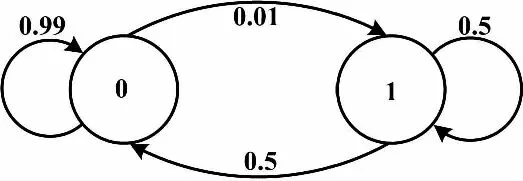
图4 马尔可夫模型
马尔可夫模型可以用概率矩阵的形式来表达,即用一个n×n维矩阵(n为状态数)来表示各个概率,定义为随机转移概率矩阵(转移矩阵),记为P。
由上述分析可得转移矩阵P的表达式为:

(1)
矩阵的每一行每一列均代表其中的一种状态,如果存在更多的状态,则可用更多的行和列来表示。位于某行某列的数字表示为由某行代表的状态到某列代表的状态的转移概率。
针对图4所示马尔可夫模型,对式(1)解释如下:第一行第一列的数字(0.99),代表下一个时间段由状态0转移到状态0(即停留在状态0)的概率;第一行第二列的数字(0.01),代表下一个时间间隔内由状态0到状态1的转移概率;第二行第一列数字(0.5)代表下一个时间间隔内由状态1到状态0的转移概率;第二行第二列的数字(0.5)代表下一个时间间隔内由状态1到状态1的转移概率。
在控制系统中,人们最关心系统预计的停机时间。以本文之前提出的多路控制器为例,则问题就转化为“求解系统在状态1时的平均概率”。求解系统在状态1的平均概率,即求解系统的不可用率。由于在同一个系统中,可用率和不可用率是一对互斥事件,因此求得系统的可用率就可得到其不可用率。
求解稳态可用率有以下3种方法。
① 树型图
树型图即画出像树杈的直观图,其简图如图5所示。先运用概率规则把每个状态发生的概率进行计算标注,再根据路径方向把标注的概率依此相乘,得到每条路径的独立概率。要得到每一种状态在该时态之后的总概率,则把给定状态下的所有路径概率相加即可。列出不同时间段的状态概率,在图中寻找状态1的概率,然后把得到的概率相加,就可求得停机时间(即不可用率)。在任何时间段,所有状态概率之和为1,运用这一原理可以检验计算过程是否出错。这种树型图方法计算繁琐,容易出错,不适用于实际规模的马尔可夫模型求解。

图5 树型图简图
② 计算稳态概率
转移矩阵P(n×n维矩阵)表示在一个时间段内由一种状态转移到另一种状态的概率。这个矩阵可以与自身相乘,而得到多个时间段的转移概率。
计算过程中,当P做平方运算时,其结果为一个n×n维矩阵。2步状态之间的转换概率可表示为:
如果上述结果矩阵左乘以P,就可以获得3步状态之间的转移概率,即:

(2)
这个过程一直继续到获得n步概率转移矩阵,在不断相乘后,得到的每一步之间的变化会越来越小,如18步状态之间转移概率为:


(3)
由式(3)可以得到:P18=P17,即P17+1=P17。最后到达Pn+1=Pn,矩阵中的数值不再变化。记不再随时间段而变化的矩阵为PL,该矩阵被称为“极限状态概率”矩阵。此时极限状态概率矩阵的上行和下行都是相同的数,即第n步进入状态0的概率是相等的,表示该方法计算时与起始状态无关。但是,实际起始状态仍会影响时变概率。采用第三种方法可以很好地解决上述问题。
③ 代数关系直接求解
起始状态概率是以行矩阵表示的(1×n矩阵)。这个行矩阵是一个数值表,它表示了系统处于每一个状态的概率。设S0为起始概率表(即第0时间段)。如果一个系统总是起始于一个特定的状态,那么S0就会有一个元素为1,而其余的元素为0。
以多路控制器为对象,以检测温度为例,得出:系统总是起始于状态0。因此,起始概率S0=[1 0],对于任何特定时间段的状态矩阵Sn,可以通过Sn-1乘以P或S0乘以Pn-1得到。
通过大量的计算验证了以上结论的正确性,且当Sn+1乘以P等于Sn时,即达到极限状态概率(记为SL)。所以,可用代数关系直接求解。
当极限状态概率存在时,有:
(4)

如果对式(4)做矩阵乘,得到代数关系为:
(5)
由式(5)得到:
(6)
又因为在同一个系统内出现的两个状态为互斥事件,所以有:
(7)
结合式(6)和式(7)得到:
(8)
最后得到结果为:
(9)

3 结束语
本文简述了ARM多路控制器的特点,并且以该
控制器监测温度为实例,建立马尔可夫模型,分别运用3种不同的极限概率(即稳态概率)计算方法求解马尔可夫模型。经过对比得出,直接代数法是最快并且最符合实际(误差最小)的求解方法。
在可维修系统中,随着时间段的增加,概率值的变化越来越小,最终概率值逐渐到达稳态。此时就可以得到系统的稳态可用率,该稳态可用率为日后维修和检测提供了安全保证[9]。目前,在系统设计时,为了得到最优方案,必须综合考虑设计约束条件,控制系统的安全性和可靠性是重要的设计约束条件;在优化过程中,则需要考虑安全性和可靠性的量化指标和定量评估方法,通过马尔科夫模型的建立与求解该模型,则可定性地分析系统的安全性与可靠性。相信有了统一的控制系统[10-12]设计的安全性和可靠性参数,就能真正实现对控制系统安全、可靠的设计。
[1] 陈高翔,冯冬芹.安全仪表系统硬件失效概率的评估方法[C]//第八届工业仪表与自动化学术会议集(上),2007.
[2] 田泽.嵌入式系统开发与应用[M].北京:北京航空航天大学出版社,2005:208-619.
[3] 程韬波,曾敏,吕小青,等.磨具多路温度控制器的研制与分析[J].机电产品开发与创新,2004,17(5):81-83.
[4] 史健芳.智能仪器设计基础[M].北京:电子工业出版社,2012:216-278.
[5] 周昕,林轶翚,崔远智.基于实时控制的多路温度检测系统[J].控制系统,2004,20(8):64-71.
[6] 刘志勇.工业控制器可靠性若干问题的研究与开发[D].杭州:浙江大学,2012.
[7] 胡慧芳,沈元隆.硬软件交互的可靠性建模及应用[J].微型机与应用,2011,30(5):64-66.
[8] Goble W M.控制系统的安全评估与可靠性[M].北京:中国电力出版社,2008:95-239.
[9] 林澜,马坚勇.智能仪表中运用抗干扰措施的体会[J].自动化与仪表,2004(5):23-27.
[10]马中梅,马广云,徐英慧,等.ARM嵌入式处理器结构与应用基础[M].北京:北京航空航天大学出版社,2002:60-89.
[11]刘建昌,于红磊,辛红,等.S7-00/400 PLC工业网络通信技术指南[M].北京:机械工业出版社,2009.
[12]王啸东.PLC 控制系统设计方法解析[J].自动化与仪器仪表,2011(1):43-48.
