异步牵引电机逆解耦中的零动态分析
2014-04-03,2
,2
(兰州交通大学自动化与电气工程学院1,甘肃 兰州 730070;兰州交通大学光电技术与智能控制教育部重点实验室2,甘肃 兰州 730070)
0 引言
目前,交流异步牵引电机已经广泛应用于CRH系列的高速动车组。异步牵引电机是一个十分复杂的非线性控制对象[1]。由于变量之间存在交叉耦合,要提高交流牵引电机的控制性能[2],必须使感应电机的转速和转子磁链实现动态解耦。逆系统解耦控制方法[3]是一种非线性反馈线性化方法,具有直观、简便和易于理解的特点。已经有学者将逆系统控制方法引入交流调速领域,实现了定子磁链和电磁转矩的动态解耦控制[4-6]。
在采用逆系统方法对异步牵引电机进行线性化解耦的过程中,当系统相对次数γ小于系统阶数n时,通过坐标变换,从原动力学系统中分隔出零动态子系统。零动态是系统的内部动态行为,其与系统的稳定性存在密切联系,如果零动态方程不稳定,则线性化后的对象也是不稳定的,所以对γ 文献[7]和[8]在异步电机直接反馈线性化中讨论了零动态问题;文献[9]分析了非线性系统的一阶零动态的稳定性;文献[10] 研究了直流电动机非线性控制中的零动态特性。本文阐述了当γ 考虑如下非线性系统: (1) (2) 式中:x为n维状态向量;f(x)和g(x)均为n维光滑向量场;ui为第i个控制量;yi为第i个输出量;hi(x) 为x的标量函数。 对于每一个输出yi=hi(x)都有一个对应的相对次数γi,而系统相对次数γ=γ1+γ2+…+γm。现假设系统相对次数γ=γ1+γ2+…+γm (3) 在上述变换作用下,系统(1)和(2)可以变换为: 由于系统相对次数γ小于系统阶数n,那么在采用式(3)的坐标变换后,可以得到剩下的(n-γ)个映射关系,用η可表示为: η=[zγ+1,zγ+2,…,zn]T=[η1,η2,…,ηn-γ]T (4) 使得向量函数φ(x)在x=x0处的Jacobian矩阵是非奇异的。 一般来说,可以适当选择系统输出函数hi(x),使其在平衡点x0处的值为零,即hi(x)=0;而输出yi=hi(x)实质上是系统的实际输出动态响应相对于平衡点输出函数的动态偏差。如果采用控制方法强迫使系统输出量的动态偏差任何时候都为零,这意味着在任何干扰作用下系统的输出都保持不变,从外部动态角度来看,这时系统是高度稳定的。所以令系统(1)和(2)输出表达式为: y1=y2=…=ym=0 (5) h1(x)=h2(x)=…=hm(x)=0 (6) 进而有: (7) 将式(7)代入式(3),经过变换后,前γ个方程将消失,只剩下动态方程: (8) 式(8)这组微分方程描述的正是系统的内部动态行为,所以称这组决定系统内部动态行为的方程组为原系统(1)和(2)的零动态方程组,简称为零动态。 最后需要通过数值分析方法检验系统零动态方程的稳定性,如果零动态方程在x0处是稳定的,则整个系统在x0的领域内是稳定的。 采用逆系统方法对建立在静止(α-β)坐标系下的异步牵引电机5阶非线性模型进行线性化,可实现异步牵引电机的转速和转子磁链的动态解耦。 (9) 系统输出方程为: (10) 式中:ω为电机转子转速;ψa和ψb为转子磁链。 采用逆系统方法对牵引电机系统进行解耦,需要确定系统的相对阶来判别系统是否可逆,根据式(10)进行如下计算: 根据文献[11]中给出的系统可逆的充要条件可知: (11) (12) (13) 由于异步牵引电机系统相对次数的代数和满足: (14) γ小于系统的阶数,必然会出现(n-γ)个零动态方程,采用坐标变换z=φ(x)=[z1,z2,z3,z4,z5]T,可得: (15) 其中第5个状态变量选取为转子磁链矢量的幅角。 根据式(8)可求取系统的零动态方程为: (16) 对式(16)进行如下计算: (17) 根据坐标变换z=φ(x),将式(17)的状态变量x进行z转换,可得: (18) 为了验证逆解耦后系统的稳定性,需要验证式(18)零动态方程的稳定性,只有确保零动态方程的稳定性,异步牵引电机逆解耦线性化才是有效的。一般情况下,应先求取系统的平衡状态,再根据零动态的定义将变换后零动态方程的前γ个变量值取为零后代入式(18),最后求取零动态方程的特征根。根据特征根是否都具有负实部,判别系统在平衡状态是否渐近稳定。 本文考虑异步牵引电机控制目标是使电机转子转速和转子磁链幅值满足期望值,所以取电机转子转速的给定值ωref和转子磁链幅值的给定值ψref作为平衡点,强制系统达到工作平衡点,则零动态方程变为: (19) 从式(19)可以看出,状态变量z5是随时间不断增长的,在Lyapunov稳定意义下是发散的,但其状态的实际物理意义是转子磁链矢量的幅角,它的不断增长不影响实际系统的稳定性。在实际控制系统中对于与储能环节没有直接关系的状态变量,例如角度和位移随时间的不断增长不会破坏系统的稳定性。由文献[7]可知,系统的零动态是渐近稳定的,此时如果系统外部动态也是渐近稳定的,那么整个系统是渐近稳定的。 本文分析了当γ 从实际应用的角度来看,用户主要关心的是系统的外部动态,要求外部动态不仅稳定而且要有优良的品质,而内部动态只需要稳定即可。因此,只需要在设计控制规律时保证零动态的稳定性,而对于原非线性系统就没有必要将其全部线性化,只需要线性化其影响外部动态的一部分即可。这种方法将有效简化基于逆系统方法的异步牵引电机线性化解耦过程。 [1] 张龙,郭世明.动车组电机与电器[M].成都:西南交通大学出版社,2009:76-77. [2] 宋雷铭,杨中平.动车组传动与控制[M].北京:中国铁道出版社,2009:8-11. [3] 李擎,杨立永,李正熙,等.异步电动机定子磁链与电磁转矩的逆系统解耦控制方法[J].中国电机工程学报,2006,26(6):146-150. [4] 巫庆辉.感应电动机定子磁链与转矩的逆解耦及存在性[J].控制理论与应用,2009,26(9):983-987. [5] 巫庆辉,伦淑娴.基于定转子电阻误差补偿的感应电动机自适应逆解耦控制研究[J].自动化学报,2010,36(2):297-303. [6] 巫庆辉,伦淑娴,常晓恒,等.基于主元分析神经网络补偿的感应电动机逆解耦控制[J].电工技术学报,2011,26(1):40-45. [7] 张春朋,林飞,宋文超,等.基于直接反馈线性化的异步电动机非线性控制[J].中国电机工程学报,2003,23(2):99-102. [8] 郭春平,王奔,赵岳恒,等.异步电机反馈线性化解耦控制[J].大电机技术,2010,(4):31-37. [9] 朱晓荣,彭咏龙,李和明,等.电流型PWM整流器的非线性控制[J].中国电机工程学报,2007,27(28):96-101. [10]鲁芳,孙美美,周磊.直流电动机的非线性控制研究[J].现代电子技术,2011,34(24):202-205. [11]张兴华,戴先中.基于逆系统方法的感应电机调速控制系统[J].控制与决策,2000,15(6):708-711.1 多输入多输出非线性系统的零动态

2 异步牵引电机逆解耦的零动态分析
2.1 基于逆系统方法的异步牵引电机线性化解耦

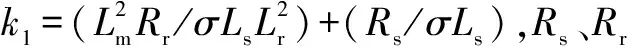

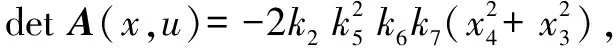

2.2 零动态方程的求取
2.3 零动态方程的稳定性检验
3 结束语
