某武器系统测量设备标校周期优化研究
2014-04-03
(山东烟台海军航空工程学院,山东 烟台 264001)
0 引言
某型舰空导弹武器为引进装备,自引进以来都是根据生产方提供的标校周期(也称校准间隔或校准周期)进行标校。但由于工作环境不同和服役年限的增加,武器的标校周期是否符合实际情况需要进行验证。目前,关于标校周期的研究多集中于测量系统。校准周期的确定方法一般分为两类:一类是根据统计数据进行制定或优化,这需要大量的历史数据做支持,如文献[1]和[2]。另一类是利用灰色预测方法,对于具有小样本性质的校准数据进行预测,如文献[3]~[6]。统计模型的方法对于引进武器来说,没有足够的数据支撑;灰色预测模型针对单调的序列具有较好的效果,但是对于具有复杂变化规律的武器系统校准数据预测效果较差。本文通过历史校准数据对武器系统的标校周期进行优化,分析了历史校准数据的特征,并对校准数据进行了数学描述和预测。
1 标校的数据模型
1.1 标校原理
标校的主要目的是对武器的系统误差进行测量、评估,确定系统的运行状态并采用相应的误差补偿方案对系统误差进行消除。标校的基本方法是采用被校准设备和高精度的设备同时测量同一目标,当高精度设备的精度是被校准设备的3倍以上时,可以以高精度设备的测量结果作为真值,进行误差的分析。标校数据包括真值和观测值,真值与观测值的差yi为校准数据,yi含有系统误差和随机误差,其数学模型如下:
yi=sri+rri
(1)
式中:yi为总误差;sri为系统误差;rri为随机误差。系统误差反映了仪器设备随自身惯性、使用时间、环境等因素影响引起的长期确定性变化趋势,随机误差则表明了测量系统的随机波动情况。
1.2 数据特点及建模思想
由式(1)可知,校准数据由趋势项和随机波动两部分组成。某武器系统的引进时间较短且数量较少,测量设备的结构复杂,使得误差特性复杂,因此校准数据具有小样本、非线性的特点。校准周期确定的难点是如何根据历史的小样本数据建立合适的预测模型,来预测下几个校准时刻的误差,从而优化校准周期,使武器系统的测量设备发挥其最优性能。如果预测得到的校准参数在规定的精度要求之内, 表明武器系统的这项参数状态良好,可以适当延长标校周期;否则,认为武器系统在标校周期内的误差可能超出正常范围,应适当缩短标校周期。为了保证预测数据的可靠性,一般仅预测现有时刻以后的1~2个参数。针对校准数据的特点,本文提出基于EMD-SVM-GM的组合预测方法,从而发挥各自预测方法的优势,使预测结果更加准确,为标校周期的优化提供较好的理论支撑。
2 EMD-SVM-GM模型
2.1 组合预测模型
根据校准数据特点,趋势项一般为单调或周期函数,而随机波动项符合统计特性,但是样本数量较少,无法进行统计估计。如果直接对误差进行建模并估计,可能因为小样本和非线性等特性,使得预测的误差偏离正常值,所以本文尝试首先将非线性数据用经验模态分解(empirical mode decomposition,EMD)方法进行处理,然后再进行预测。EMD方法是一种新的非线性数据处理方法,它可以将非线性非平稳序列分解为一系列固有模态函数(intrinsic mode function, IMF)分量和残余分量。IMF分量可以认为是随机波动项,选用针对小样本估计的最佳理论——支持向量机(support vector machine,SVM)方法对其处理;分离所得的残余量往往符合单调特性,适合用单调序列的预测方法,本文选用GM(1,1)模型进行预测。组合预测的模型如图1所示。
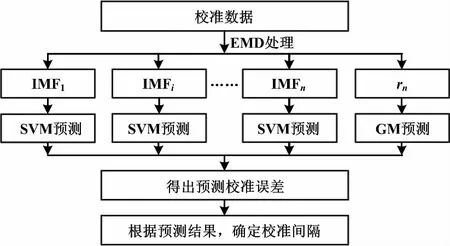
图1 组合预测模型图
假设校准数据为m个,组成的时间序列为x={x1,x2,…,xm},其经过EMD分解得相应分量。对每个IMF分量进行SVM预测,为每个IMF分量建立SVM模型并进行一步预测,对于每个imfi预测的随机成分为SVM_prei;对于rn采用GM(1,1)模型进行处理,得到预测数据为GM_p。综合两种预测结果,得到一步预测结果为:
(2)
式中:n为IMF分量个数;m为校准数据个数。
为比较模型的预测能力,采用均方差(mean square error,MSE)进行评价,其表达式如下:
(3)
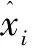
2.2 EMD方法
1998年,美国宇航局的N.E.Huang等在瞬时频率概念的基础上提出了一种新的信号处理方法——基于EMD的时频分析方法。它可以处理非线性和非平稳信号,在分解时基函数不确定,只依赖于数据本身,具有良好的自适应特点。EMD方法将数据看作是由一个或多个固有模态函数组成。由于经验模态分解方法的这些优点,使得它在生物、海洋、地球科学、天文学和工程技术等领域中得到了广泛应用。校准数据往往具有非线性的特点,EMD为处理这些复杂多变的数据提供了一种新的方法。
经过EMD方法分解得到的IMF具有如下特性。
① 在整个信号上,极值点的个数和过零点数目相等或最多相差一个;
② 局部均值为零,即由局部极大值构成的上包络线和由局部极小值构成的下包络线的平均值为零。
针对EMD方法的分解步骤,可参阅文献[7],在此不予赘述。本文采用法国学者Riling的分解准则[8]。原数据x(t)经过EMD方法分解得到:
(4)
式中:imfi为分解得到的IMF分量;rn为残余分量。
2.3 支持向量机理论
2.3.1 最小二乘支持向量机回归原理
SVM是一种建立在统计学习理论和VC(Vapnik Chervonenkis)维理论基础上,运用结构风险最小化原则的机器学习方法[9]。针对小样本情况,它有效地克服了局部极小点、维数灾难以及过拟合等传统算法所不可避免的问题。最小二乘支持向量机(least square support vector machine,LSSVM)将SVM的优化问题转化为求线性方程组的问题,具有比标准SVM更快的训练速度。
设样本的训练集为{(xi,yi)|i=1,...,l},其中xi∈Rn为输入向量(n为空间维数),yi∈R为输出,利用非线性映射φ(·)将输入向量从原空间映射到高维特征空间,在高维特征空间中构造最优线性回归函数:
f(x)=wTφ(x)+b
(5)
最小二乘支持向量机回归算法就是求解如下优化问题:
(6)
式中:ei为回归函数值与实际值的误差;γ为常数。
引入拉格朗日函数,将上述约束优化问题转化为无约束优化问题,在对偶空间可以得到下式:
(7)
式中:αi∈R为拉格朗日乘子。
根据最优化理论中的KKT(Karush-Kuhn-Tucker)条件,可得如下等式约束:
(8)
对式(8)消去w和ei,得到如下线性方程组:
(9)
式中:E=[1,…,1]T;α=[α1,…,αl];y=[y1,…,yl]T;I为l×l阶单位阵;Ω为l×l阶矩阵,且Ωij=φ(xi)Tφ(xj)。
根据Mercer条件,定义如下核函数:
K(xi,xj)=φT(xi)φ(xj)
(10)
则式(9)变为:
设Q=Ω+γ-1I,由于Q是一个对称半正定矩阵,Q-1存在,应用最小二乘法求解上式,可得如下解:
(11)
α=Q-1(y-bE)
(12)
则最小二乘支持向量机回归函数可表示为:
(13)
2.3.2 预测原理
对前n个训练样本进行相空间重构,确定输入输出样本对和嵌入维数m,建立自相关输入xn={xn-m,xn-m+1,…,xn-1}与输出yn={xn}之间的映射关系,即f:Rm→R,得到的学习样本如下:
对支持向量机进行训练,得到最小二乘支持向量机回归函数:
(14)
由于xn-m+1=[xn-m+1,…,xn],因此可以得到一步预测模型为:
(15)
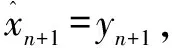
(16)
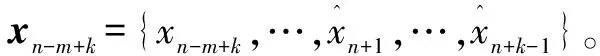
2.4 灰色预测模型GM(1,1)
单变量一阶线性灰色模型GM (1, 1) 在实际中是应用最多的模型[3]。假设原始数列为x(0)=[x(0)(1),x(0)(2),…,x(0)(n)],x(0)的1次累加(1-AGO)序列为:x(1)=[x(1)(1),x(1)(2),…,x(1)(n)],其中:
(17)
x(1)的紧邻均值生成序列为z(1)=[z(1)(1),z(1)(2),…,z(1)(n)],其中:
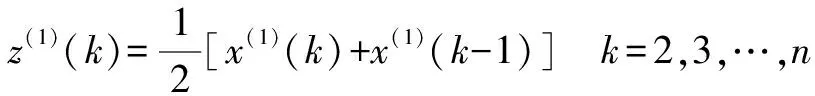
(18)
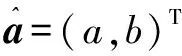
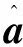
(19)
模型GM(1,1)的预测序列为:
(20)
原序列的预测值为:
(21)
3 实例验证
3.1 测量仪器标校周期优化
当标称值为10 V 时,要求实际测量不确定度小于0.01%,校准数据如表1 所示。
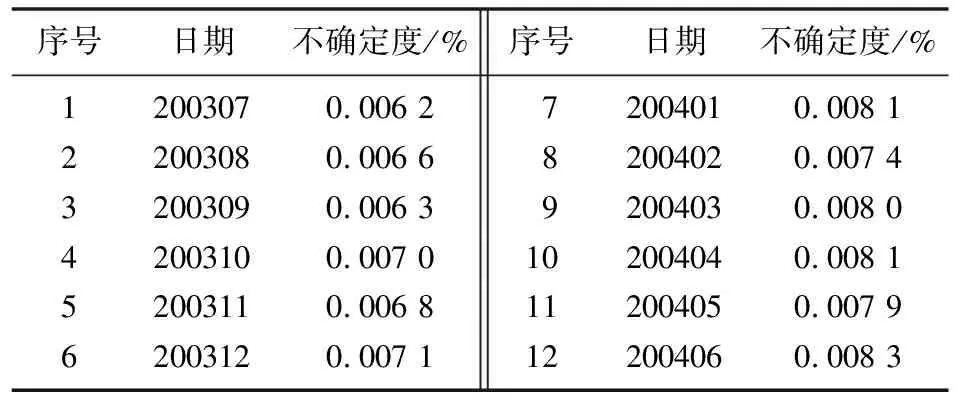
表1 校准数据
仿真取前10个数据用于模型的建模,后两个数据进行预测,各个方法的均方差如表2所示,其预测的图形如图2所示。
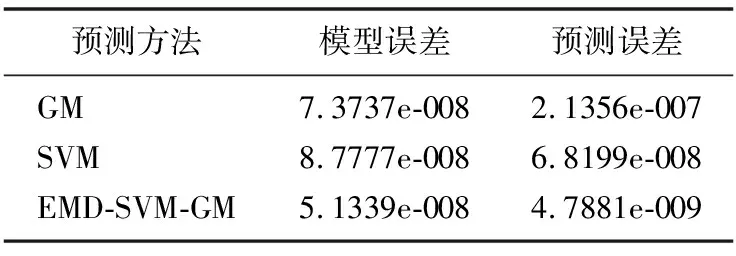
表2 预测均方差
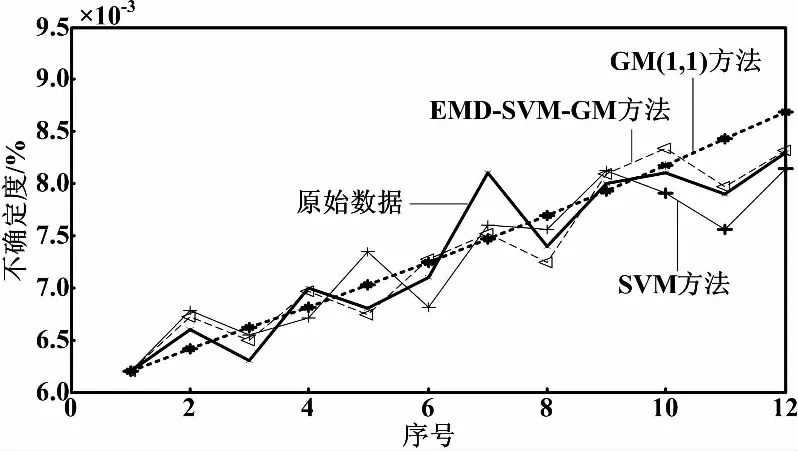
图2 各种预测方法比较图
3.2 某武器系统标校周期优化
某武器系统由于引进的时间较短,所采集的校准数据较少。根据标校规程,每三个月对其测量设备的距离参数进行一次静态标校,其测量目标的最大允许误差为6 m,得到符合要求的历史校准数据。对这些数据采用本文方法进行建模和预测。经过处理,建模的误差为0.038 74,建模精度较高;其一步预测的数据为5.485 m,在最大误差范围内,不需要缩短标校周期。但是,校准误差呈增大的趋势,因此在以后标校过程中要密切关注误差的变化情况。
4 结束语
对武器系统进行标校是武器在使用过程中的重要环节,由于武器使用的状况和环境不同,标校周期的确定是应该引起重视的重要问题。校准数据序列可以用一个适当的数学模型描述,建立历史校准数据序列仿真模型,预测武器系统的性能变化趋势,从而确定下次标校时间。本文将EMD、SVM和GM方法恰当地运用于标校数据的处理中,发挥了各种方法的优势,从而取得了较好的预测效果,保证了辅助决策的质量,有助于部队保障能力的提升。
[1] 田旭光,蔡金燕,陈泽峰.基于随机过程的测量仪器校准时间间隔的确定[J].军械工程学院学报,2007,19(6):28-31.
[2] 汪静,张玘.基于新息的威布尔模型自动测试系统校准周期优化[J].电子测量与仪器学报,2011,25(2):159-163.
[3] 孙群,赵颖,孟晓风.基于灰色组合模型的校准间隔优化仿真[J].系统仿真学报,2008,20(9):2296-2298.
[4] 赵瑞贤,孟晓风,王国华.基于灰色马尔柯夫预测的测量仪器校准间隔动态优化[J].计量学报,2007,28(2):184-187.
[5] 孙群,赵颖,孟晓风.基于新陈代谢GM(1,1)模型的校准间隔预测[J].测试技术学报,2007,21(3):232-235.
[6] Huang N E.Review of empirical mode decomposition[C]∥Proceedings of SPIE,Olando,USA,2001:71-80.
[7] Rilling G,Flandrin P,Goncalves P.On empirical mode decomposition and its algorithms[C]∥IEEE-EURASIP Workshop on Nonlinear Signal and Image Processing,Grado,Italy,2003:811-815.
[8] 刘如峰,李世平,文超斌,等.基于线性趋势模型与LSSVM的校准间隔组合预测[J].传感器与微系统,2010,29(9):61-63.
[9] 孙群,赵颖,孟晓风.基于支持向量回归的自动测试系统校准间隔动态优化[J].兵工学报,2009,30(1):76-80.
