时间序列分析法在突发公共卫生事件网络舆情分析中的应用研究*
2014-04-03山东潍坊医学院261053滕文杰
山东潍坊医学院(261053) 滕文杰
近年来,突发公共卫生事件频繁发生,严重损害公众生命健康,危及社会安全稳定。在突发公共卫生事件发生发展过程中,网民关注与传播成为主要推进因素,往往迅速演化为网络舆情,并引发和带动社会舆情的升温。由于突发公共卫生事件具有明显的时间节点,网民的关注也随着时间的推进而出现量的变化,由此引发的网络舆情的变化可以看做一组时间序列资料。本研究运用时间序列分析中的ARIMA(p,d,q)模型[1](差分自回归移动平均模型,autoregressive integrated moving average),对突发公共卫生事件网络舆情网民关注度进行趋势分析和预测,分析网络舆情的传播规律,提出针对性的应急策略。
资料与方法
1.研究对象
选取2011年以来发生的典型突发公共卫生事件作为研究对象,分析其网络舆情的变化。事件的选择参考了原国家卫生部发布的2012年中国卫生十大新闻[2]、中华医学会公共卫生分会等机构评出的2011年~2012年十大公共卫生事件[3]等,遴选确定了11个典型事件:瘦肉精、染色馒头、地沟油、皮革奶、蒙牛黄曲霉素、碘盐防辐射、白酒塑化剂、毒胶囊、黄金大米、尘肺乡、毒生姜。
2.数据来源
利用百度指数搜索指数(即用户关注度)[4]收集数据。搜索指数反映了网民对相应关键词在一定时期的关注度。搜索指数关注度指标能够比较有效地反映突发事件网络舆情的变化情况[5]。分别以11个典型事件作为关键词,利用百度搜索指数,收集各事件在事件发生前一天开始、到事件发生后60天内的网络关注度数据,构成11组时间序列资料。
3.研究方法
(1)构建平均数时间序列
为分析11组时间序列资料的发展规律,采用事件发生点作为统一的时间点,组成一一对应的数据点,分别取各对应点的均值,构成平均数时间序列。平均数时间序列能够反映现象一般水平的发展变化过程和趋势[6]。
(2)ARIMA(p,d,q)模型[1]
ARIMA(p,d,q)模型主要用于非平稳时间序列的随机分析,实质上是差分运算和ARMA模型(自回归移动平均模型,autoregressive moving average)的组合,p,q为自相关和移动平均阶数,d为差分次数。任何非平稳序列只要通过适当阶数的差分实现差分后平稳,就可以对差分后序列进行ARMA模型拟合。
ARIMA(p,d,q)模型建模主要包括以下步骤:对原始序列进行平稳性检验;对非平稳序列进行差分运算;对平稳d阶差分序列进行白噪声检验;对平稳非白噪声差分序列拟合ARMA模型;对残差序列进行检验。整个统计分析借助SAS软件实现。
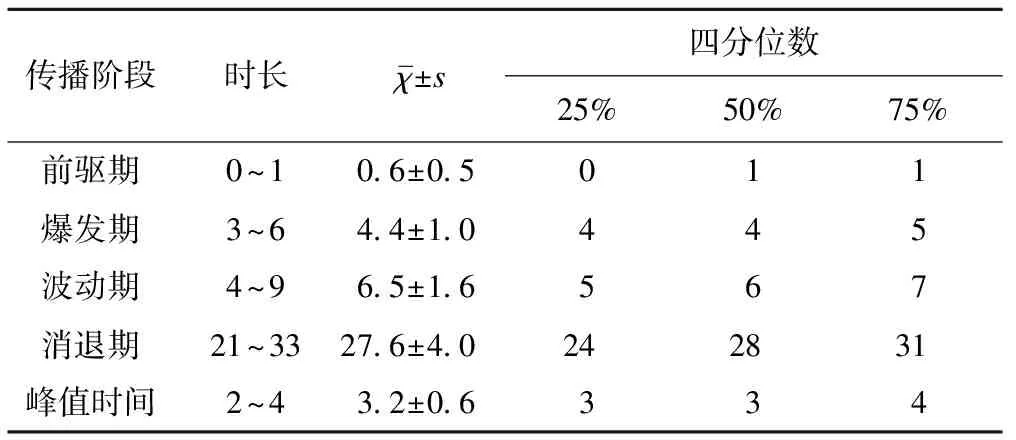
模型是指d阶差分后自相关最高阶数为p,移动平均最高阶数为q的模型,通常包含p+q个独立的未知系数:φ1,…,φp,θ1,…,θq。如果模型中有部分自相关系数φj(1≤j 根据11组原始时间序列数据,构建平均数时间序列做时序图,显示该序列有明显递减趋势、无周期波动,为非平稳序列(图1)。 图1 突发公共卫生事件网络舆情关注度时序图 对原始序列进行1阶差分,差分后序列在均值附近比较稳定地波动,没有明显趋势,基本认为是平稳的。对平稳的一阶差分序列进行白噪声检验可以看出延迟6阶和12阶时,P值均<0.05,说明差分后序列不是纯随机序列,具有短期相关性,可以进行建模分析(见表1)。 表1 突发公共卫生事件网络舆情关注度1阶差分后序列白噪声检验 考察1阶差分后序列的自相关图和偏自相关图,由于随机性影响并没有呈现明显的截尾性,因此采用最小信息准则BIC进行最优定阶,从所有阶数范围内采用SAS程序MINIC定阶命令进行最优定阶。经分析,发现自回归阶数p=5时,移动平均阶数为4时,BIC为最小(11.87294)。因此,尝试构建ARIMA(5,1,4)模型。采用条件最小二乘法识别模型系数,进行参数显著性检验发现,p=1,3,4,5,q=4时,参数都不显著。p=2,q=1,2,3时,参数显著。因此,需要建立一阶差分自回归移动平均疏系数模型即ARIMA((2),1,(1,2,3))。 用SAS软件重新进行模型定阶运算,构建一阶差分自回归移动平均疏系数模型即ARIMA((2),1,(1,2,3)),参数估计结果见表2,P值均<0.05。模型表达式为(1-0.4616B2)(1-B)xt=(1+0.69127B-0.81438B2-0.79934B3)εt。 表2 突发公共卫生事件网络舆情关注度ARIMA((2),1,(1,2,3))参数估计结果 对模型进行残差纯随机性检验,发现延迟6,12,18,24阶时P值分别为0.1545,0.7884,0.9819,0.9995,均>0.05,也就是模型通过残差自相关性检验,可以认为模型拟合效果良好。模型拟合效果见图2。 图2 突发公共卫生事件网络舆情关注度ARIMA((2),1,(1,2,3))模型拟合效果图 根据危机生命周期理论,突发性公共卫生危机通常遵循特定的生命周期,经典的是美国危机管理学家Steven Fink 1986年提出的四阶段模型:前驱阶段、急性阶段、慢性阶段、治愈阶段[7]。根据这一理论,分析拟合曲线的转折、降消特点,呈现明显的上升、达到高峰,下降、反复波动,消退、低位震荡、趋于稳定的特征,因此将突发公共卫生事件网络舆情分为四个阶段:前驱期、爆发期、波动期、消退期。前驱期指事件发生节点到网络舆情急剧升温前的折点;爆发期指网络舆情出现第一个完整高峰的时长;波动期指舆情反弹、高位波动、表现第2峰或多峰的时长;消退期指持续下降、低位震荡、趋于稳定的时长。网络舆情的消退呈现一个长尾特性,而且网络舆情关注度很难下降到发生前的水平。从网络舆情的监控来讲,将舆情下降到接近事件发生前的水平并趋于稳定作为消退期的终结。示意图如图3。 图3 突发公共卫生事件网络舆情传播阶段示意图 根据传播阶段的划分和11组突发公共卫生事件网络舆情关注度原始数据时序图,分别统计各阶段的时长,用均值(反映集中趋势)和四分位数(反映离散趋势)表示11组数据总体传播阶段的变化情况。结果显示,突发公共卫生事件网络舆情前驱期很短,平均0.6天,有一半事件没有前驱期,呈现急剧升温现象;爆发期平均4.4天,多数为4天;波动期平均6.5天;消退期平均27.6天;到达峰值的时间平均3.2天,多数为3天(表3)。 表3 突发公共卫生事件网络舆情传播阶段时长(天数) ARIMA模型是经典的时间序列分析方法,主要用于随机平稳时间序列拟合建模和外推预测。由于ARIMA模型是对连贯的历史数据的分析,数据量越大,模型越准确。差分运算是非平稳序列平稳化的主要途径,差分阶数的选择主要依据原始序列的特定规律,识别线性趋势、曲线趋势、固定周期趋势选择合适的差分方式,但差分运算的阶数要适当,避免过差分,而导致大量信息的损失。另外,疏系数模型的选择,要在传统定阶方法的基础上,进行反复尝试,删除不显著的参数,逐步优化模型,构造疏系数模型。本例中,突发公共卫生事件网络舆情作为时间序列的大数据资料,ARIMA模型能够得到很好的应用,拟合效果较好。 根据突发公共卫生事件网络舆情的传播规律,危机应对应把握以下几点:①前驱期很短,事件发生第一天是舆情应对的“黄金期”。应对时间越早、措施越得当、声音越及时,影响越小,整个周期越短。②高峰期是网络舆情监控和应对的关键期,呈现“4天规律”。在高峰期的上升期,即事件发生的第2、3天,是危机应对的“第一关键期”,处理及时,应对得当,可以使舆情产生“拐点”,降低峰值,缩短时长。在高峰期的下降期,即事件发生的第4、5天,是危机应对的“第二个关键期”,处理得当,可以迅速降低舆情热度,缩短波动期时长,甚至可以阻止波动期出现,直接进入消退期。③波动期表现为舆情的反复,是危机应对的“强化期”,相关处理措施应及时跟进,尽快推进舆情进入消退期。④前三个阶段是危机应对的重点阶段,总体呈现“10天规律”,应把握关键环节,综合应对,主导网络话语权,引导事件和舆情发展方向。但应注意,网络舆情的四阶段传播,仅是一般规律的反映,会受到危机应对等因素的影响,可能带来某一阶段时长的缩短甚至消除,应根据特定事件具体分析。 参 考 文 献 1.王燕.应用时间序列分析.北京:中国人民大学出版社,2008:146. 2.国家卫生计生委.2012年中国卫生十大新闻[EB/OL].(2013-01-10)[2014-3-20].http://www.moh.gov.cn/wsb/pxwfb/201301/d184d25bce2040abb9553606e658fd2c.shtml. 3.人民网.2011-2012年公共卫生十大新闻热点[EB/OL].(2012-05-11)[2014-3-20].http://medicine.people.com.cn/GB/135395/17860890.html. 4.百度.百度搜索指数[EB/OL].[2014-3-20].http://index.baidu.com/Helper/?tpl=help&word=%CA%DD%C8%E2%BE%AB. 5.陈涛,林杰.基于搜索引擎关注度的网络舆情时空演化比较分析-以谷歌趋势和百度指数比较为例.情报杂志,2013,32(3):7-10. 6.杨国良.统计学原理.第1版.重庆:重庆大学出版社,2006:159. 7.叶金珠.网络突发事件蔓延及干预研究.武汉:华中科技大学,2012:40.结果与分析
1.原始序列时序图
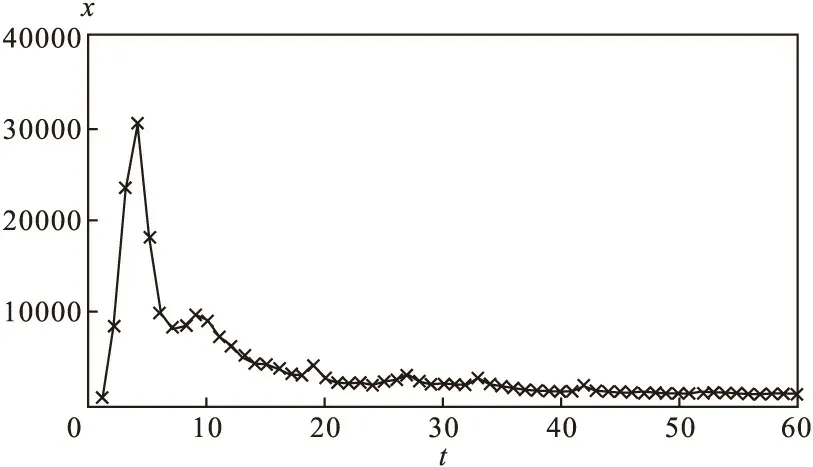
2.差分运算及白噪声检验

3.相对最优定阶及模型建立
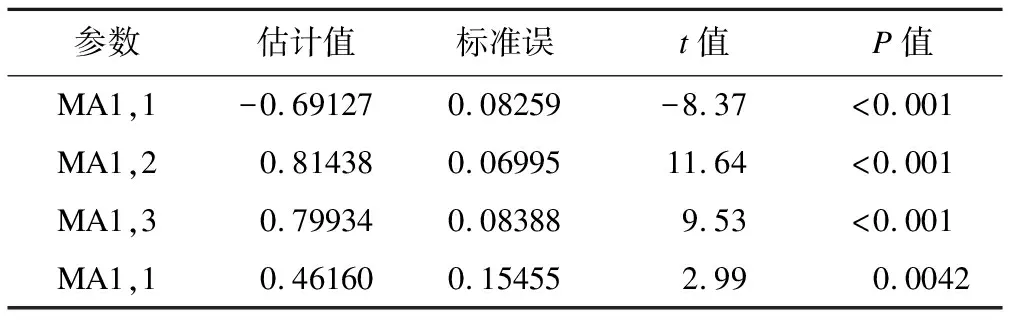
4.构建疏系数模型ARIMA((2),1,(1,2,3))
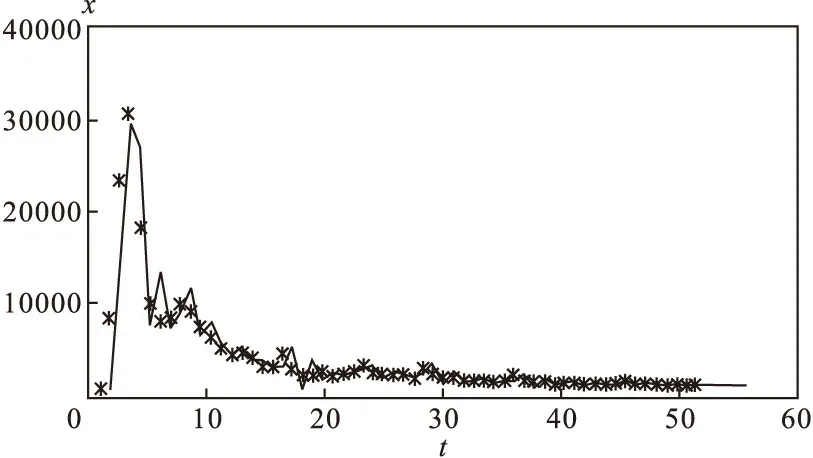
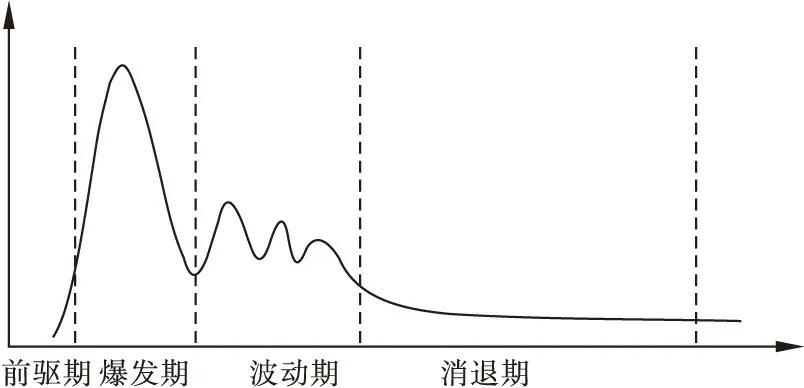
5.网络舆情传播规律分析
6.网络舆情传播阶段的时长分析
讨论与建议
1.ARIMA模型的应用
2.突发公共卫生事件网络舆情的应急策略
