关于四次整系数不可约多项式

徐蕾蕾，黎爱平

(上饶师范学院，江西 上饶 334001)

设f(x)=x4+p3x3+p2x2+p1x+1是一个整系数多项式，本文就以下各种情况对f(x)在有理数域上可约或不可约的问题进行了研究，给出了f(x)可约或不可约的判定条件。

(1)情形1：p3=0，p2=0，p1=0，定理1；

(2)情形2：p3=0，p2=0，p1≠0，定理1；

(3)情形3：p3=0，p2≠0，p1=0，定理2；

(4)情形4：p3=0，p2≠0，p1≠0，定理3；

(5)情形5：p3≠0，p2=0，p1=0，定理4；

(6)情形6：p3≠0，p2≠0，p1=0，定理4；

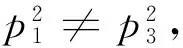
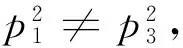
定理1.设f(x)=x4+px+1是整系数多项式，则

当p=2或p=-2时，f(x)在有理数域上可约。反之,f(x)在有理数域上不可约。

证明：当p=2时，f(x)=x4+2x+1=(x+1)(x3-x2+x+1)，

当p=-2时，f(x)=x4-2x+1=(x-1)(x3+x2+x-1)，即f(x)在有理数域上可约。

当p=0时，显然f(x)在有理数域上不可约。

当p≠0时，若p≠2且p≠-2，则f(x)没有有理数根，即f(x)在有理数域上不能有一次因式。假定f(x)在有理数域上可约，根据因式分解定理，则f(x)只能分解成两个一元二次整系数多项式的乘积，设为

f(x)=(x2+ax+b)(x2+cx+d)

其中a,b,c,d均为整数。

即x4+px+1=x4+(a+c)x3+(ac+b+d)x2+(ad+cb)x+bd。

从而

当b=1且d=1时，p=a+c=0与p≠0相矛盾，故f(x)在有理数域上不可约。

当b=-1且d=-1时，p=-(a+c)=0与p≠0相矛盾，故f(x)在有理数域上不可约。

综上所述，当p=2或p=-2时，f(x)在有理数域上可约，否则f(x)在有理数域上不可约。

推论1.1.设f(x)=x4+px+1(p≠0)是整系数多项式，若f(x)无整数根，则f(x)在有理数域上不可约。

证明：因为f(x)无整数根，所以f(x)在有理数域上不能分解成一次因式之积。因为p≠0，由定理1的证明可知，f(x)又不能分解成两个一元二次整系数多项式的乘积。即f(x)在有理数域上不可约。

定理2.设f(x)=x4+px2+1(p≠0)是整系数多项式，则

(1)当p=-2时，f(x)在有理数域上可约；

(2)当p≤-2，且-2-p是一个有理数的平方或2-p是一个有理数的平方，f(x)在有理数域上可约；

(3)除上述情况外,f(x)在有理数域上不可约。

证明: (1)当p=-2时，f(x)=x4-2x2+1=(x2+1)(x2-1)=(x+1)(x-1)(x2+1),即f(x)在有理数域上可约。

(2)当p≤-2时，且-2-p是一个有理数的平方，

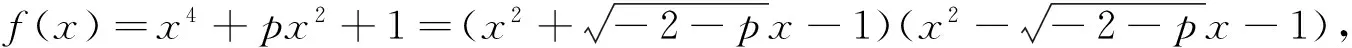
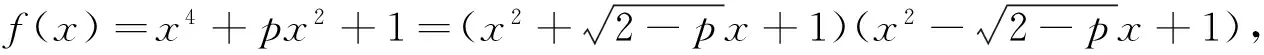
(3)除上述情况外，因为f(x)没有有理数根，则f(x)在有理数域上不能有一次因式。假定f(x)在有理数域上可约，根据因式分解定理，则f(x)只能分解成两个一元二次整系数多项式的乘积，设为

f(x)=(x2+ax+b)(x2+cx+d)

其中a,b,c,d均为整数。即

x4+px2+1=x4+(a+c)x3+(ac+b+d)x2+(ad+cb)x+bd。

从而

当b=1且d=1时，p=a+c=0与p≠0相矛盾，故f(x)在有理数域上不可约。

当b=-1且d=-1时，p=-(a+c)=0与p≠0相矛盾，故f(x)在有理数域上不可约。

综上所述，当p=-2，以及p≤-2，且-2-p是一个有理数的平方或2-p是一个有理数的平方，f(x)在有理数域上可约。否则，f(x)在有理数域上不可约。

推论2.1.设f(x)=x4+px2+1(p≠0)是整系数多项式，若p>2，且f(x)没有整数根，则f(x)在有理数域上不可约。

证明：因为f(x)无整数根，所以f(x)在有理数域上不能有一次因式。因为p≠0且p>2，由定理2的证明可知，f(x)又不能分解成两个一元二次整系数多项式的乘积。因此f(x)在有理数域上不可约。

定理3.设f(x)=x4+p2x2+p1x+1(p1≠0)是整系数多项式，则当p2-p1=-2或p2+p1=-2时，f(x)在有理数域上可约。反之，f(x)在有理数域上不可约。

证明:当p2-p1=-2，p2=p1-2时，

f(x)=x4+(p1-2)x2+p1x+1=(x+1)[x3-x2+(p1-1)x+1]。

即f(x)在有理数域上可约。

当p2+p1=-2，p=-p1-2时，

f(x)=x4-(p1+2)x2+p1x+1=(x-1)[x3-x2-(p1+1)x-1]。

即f(x)在有理数域上可约。

当p2-p1≠-2且p2+p1≠-2，则f(x)没有有理数根，即f(x)在有理数域上不能有一次因式。假定f(x)在有理数域上可约，根据因式分解定理，则f(x)只能分解成两个一元二次整系数多项式的乘积，设为

f(x)=(x2+ax+b)(x2+cx+d)，

其中a,b,c,d均为整数。即

x4+p2x2+p1x+1=x4+(a+c)x3+(ac+b+d)x2+(ad+cb)x+bd。

从而

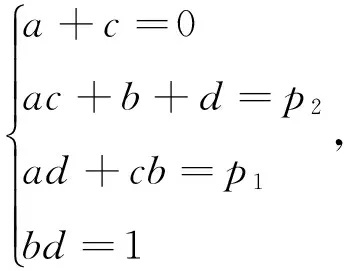
当b=1且d=1时，p2=2+ac=2-a2，c=-a,p1=a+c=0与p1≠0相矛盾，故f(x)在有理数域上不可约。

当b=-1且d=-1时，p2=-2+ac=-2-a2,c=-a,p1=a+c=0与p1≠0相矛盾，故f(x)在有理数域上不可约。

综上所述，当p2-p1=-2或p2+p1=-2时，f(x)在有理数域上可约。反之，f(x)在有理数域上不可约。

推论3.1.设f(x)=x4+p2x2+p1x+1(p1≠0)是整系数多项式，若f(x)无整数根，则f(x)在有理数域上不可约。

证明：因为f(x)无整数根，所以f(x)在有理数域上不能有一次因式。因为p1≠0，由定理3的证明可知，f(x)又不能分解成两个一元二次整系数多项式的乘积。因此f(x)在有理数域上不可约。

定理4.设f(x)=x4+p3x3+p2x2+1(p3≠0)是整系数多项式，则当p3+p2=-2或p2-p3=-2时，f(x)在有理数域上可约。反之，f(x)在有理数域上不可约。

证明:当p3+p2=-2，p2=-(p3+2)时，

f(x)=x4+p3x3(p3+2)x2+1=(x-1)[x3+(p3+1)x2-x-1]。

即f(X)在有理数域上可约。

当p2-p3=-2，p2=p3-2时，

f(x)=x4+p3x3+(p3-2)x2+1=(x+1)[x3+(p3-1)x2-x+1]。

即f(x)在有理数域上可约。

当p3+p2≠-2且p2-p3≠-2时，则f(x)没有有理数根，即f(x)在有理数域上不能有一次因式。假定f(x)在有理数域上可约，根据因式分解定理，则f(x)只能分解成两个一元二次整系数多项式的乘积，设为

f(x)=(x2+ax+b)(x2+cx+d)，

其中a,b,c,d均为整数。即

x4+p3x3+p2x2+1=x4+(a+c)x3+(ac+b+d)x2+(ad+cb)x+bd，

从而

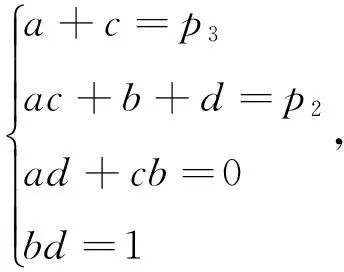
当b=1且d=1时，p2=2+ac=2-a2，c=-a,p3=a+c=0与p3≠0相矛盾，故f(x)在有理数域上不可约。

当b=-1且d=-1时，p2=-2+ac=-2-a2，c=-a,p3=a+c=0与p3≠0相矛盾，故f(x)在有理数域上不可约。

综上所述，当p3+p2=-2或p2-p3=-2时，f(x)在有理数域上可约。反之，f(x)在有理数域上不可约。

推论4.1：设f(x)=x4+p3x3+p2x2+1(p3≠0)是整系数多项式，若f(x)无整数根，则f(x)在有理数域上不可约。

证明：因为f(x)无整数根，所以f(x)在有理数域上不能有一次因式。因为p3≠0，由定理4的证明可知，f(x)又不能分解成两个一元二次整系数多项式的乘积。因此f(x)在有理数域上不可约。

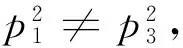
证明: 当p3+p2+p1=-2，p2=-(p3+p1+2)时，

f(x)=x4+p3x3-(p3+p1+2)x2+p1x+1=(x-1)[x3+(p3+1)x2-(p1+1)x-1]。

即f(x)在有理数域上可约。

当p2-p3-p1=-2,p2=p3+p1-2，时，

f(x)=x4+p3x3+(p3+p1-2)x2+p1x+1=(x+1)[x3+(p3-1)x2+(p1-1)x+1]。

即f(x)在有理数域上可约。

当p+p2+p1≠-2且2-p3-p1≠-2时，则f(x)没有有理数根，即f(x)在有理数域上不能有一次因式。假定f(x)在有理数域上可约，根据因式分解定理，则f(x)只能分解成两个一元二次整系数多项式的乘积，设为

f(x)=(x2+ax+b)(x2+cx+d)，

其中aa,b,c,d均为整数。即

x4+p3x3+p2x2+p1x+1=x4+(a+c)x3+(ac+b+d)x2+(ad+cb)x+bd。

从而

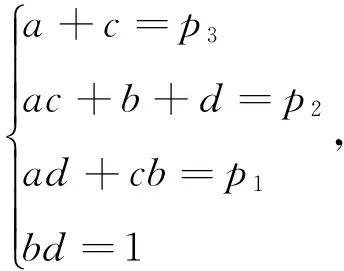
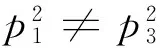
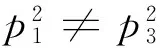
综上所述，当p3+p2+p1=-2或p2-p3-p1=-2时，f(x)在有理数域上可约。反之，f(x)在有理数域上不可约。

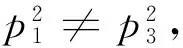
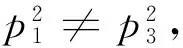
推论5.2.设f(x)=x4+p3x3+p2x2+p1x+1是整系数多项式，若f(x)无整数根，且f(x)在有理数域上可约，则p3=p1或p3=-p1。

说明：对于四次整系数多项式f(x)=p4x4+p3x3+p2x2+p1x+p0在有理数域上可约或不可约的问题，作为数学专业的本科生或中学教师的研究课题还是一件有意义的事情。

参考文献：

[1] 王萼芳，石生明．高等代数(第三版)[M]．北京：高等教育出版社，2003年．

[2] 陈侠．关于整系数不可约多项式[J]．沈阳航空工业学院学报，2004，21(1)：1～2．

[3] 罗永超.一类有理系数多项式无有理根的判别[J].贵州师范大学学报，2006，24(2)：88～91.