Time Complexity Analysis of a Kind of Hybrid Algorithms

LAI Xin-sheng

(Shangrao Normal University, Shangrao Jiangxi 334001, China)

Introduction

Hybrid algorithms are now an interesting topic in computer sciences and technology. Hybridizing different algorithms is an efficient method to get more powerful tools for solving hard problems. Many researchers have designed and are trying to design more efficient algorithms following this way of hybridization.

Though hybrid algorithms are receiving increasing attention from researchers, theoretic work on hybrid algorithms is rare. Zhou et al. analyzed a hybrid algorithm combining RandomWalk and Local (1+1) EA on a MaxSAT problem[6]. However, many theoretic research works are now focusing on base algorithms[7, 8, 9, 10, 11]. Even though, the bulk of theoretic work on base algorithms focus on the time complexity of genetic algorithms. He and Yao introduced a framework for analysis of the time complexity[12]. Lehre and Yao investigated how the interplay of mutation and selection impact the runtime of evolutionary algorithms[13], and their results showed that a correct balance between selection pressure and mutation rate is important to find the optimal solution in polynomial time. Chen et al. theoretically analyzed how the population size impact the runtime of evolutionary algorithms[14], and found that large populations may not always be useful. On unique input-output problem, Lehre and Yao investigated how the choice of acceptance criterion in the (1+1) EA and the use of crossover in the (μ+1) steady state genetic algorithm impact the runtime of EA, their rigorously analyzed results showed that changing these parameters can reduce the runtime from exponential to polynomial for some instance classes of the UIO problem[15]. For wide-gap problems with two optima, Chen et al. analyzed how selection pressure impact the runtime of evolutionary algorithms, and their results showed that low selection pressure is better for wide-gap problems with two optima[16]. Besides, a little work has been done on particle swarm algorithm. And most of theoretic work on particle swarm algorithm is about convergence of this algorithm[17, 18, 19], few of them discussed the time complexity of particle swarm algorithm.

In this paper, we investigate the time complexity of a kind of hybrid algorithms. This kind of hybrid algorithms combines two base algorithms. Both base algorithms should be able to be described by a discrete homogeneous absorbing Markov chain on the same finite discrete state space S. This requirement could be met, because both base algorithms in this kind of hybrid algorithms are used to solve the same problem. The solution space is the same, and when on a combinatorial optimization problem, the solution is usually finite and discrete. Through our analysis using Markov chain, we have obtained the boundaries of ‖mh‖∞.Here, ‖mh‖∞are the worst case of the time complexity of hybrid algorithms. These boundaries are nontrivial when parameter ω is close to 0 or 1.

The remainder of this paper is organized as follows. Section 1 describes the kind of hybrid algorithms considered in this paper, and Section 2 is the time complexity analysis of base algorithms. Section 3 is the time complexity analysis of this kind of hybrid algorithms, and Section 4 is relationship between mh, m1and m2. Finally, Section 5 presents conclusion and discussion.

1　A kind of Hybrid Algorithms

In this section, we describe the kind of hybrid algorithms, which are to be discussed in this paper. Now, we give the general form of this kind of hybrid algorithms as follows.

HybridAlgorithms(CombiningTwoBaseAlgorithms)

Begin

Initialize parameters of base algorithms 1 and 2, parameter ω and solutionsltn;

While (termination-condition does not hold) do

Follow base algorithm 1 and obtain a solutionsltn1;

Follow base algorithm 2 and obtain a solutionsltn2;

sltn:=sltn1with the probability ω, orsltn:=sltn2with the probability of (1-ω);

Wend

End

2　The Time Complexity Analysis of Base Algorithms

Since both base algorithms in this kind of hybrid algorithms could be described by a discrete homogeneous Markov chain, now let (ξt, t≥0) (ξt∈{Si;i=1,2,..., n}) be the discrete homogeneous absorbing Markov chain on a finite discrete states of {S1, S2, ..., Sn}.

Definition1 [12]. (First hitting time τi). Given a Markov chain (Xt), the first hitting time of the absorbing state set H when starting from transient state Siis defined as: τi= min{t;t≥0,Xt∈H|X0∈Si}.

Let pijbe the transition probability from state Sito Sj, and the transition probability matrix is P=(pij)n×n. Since the Markov chain is homogeneous, components of the transition matrix are independent of the time variable. The transition probability matrix P can be written in a block form as follows,

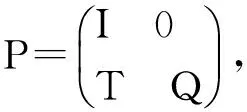
(1)

where Q is the transition probability sub-matrix among transient states, and I is the transition probability sub-matrix among absorbing states, an identity matrix, T is the transition probability sub-matrix from transient states to absorbing states, and 0 is a matrix whose entries are all 0.

Since P is a transition matrix, 0≤qij<1, (i, j=1, 2,…, n), whereqijis the entry of Q. The eigenvalues of Q are all less than 1, so, ρ(Q)=max1≤i≤n{|λi|}<1[12]. Thus the entries of (I-Q)-1are non-negative.

Theorem1[6,12,20]. Let τibe the first hitting time of Markov chain (Xt) when starting from transient state Si. Let mi=E[τi], and m=[mi]i∈T, where subscript T denotes the set of transient states. We have m=(I-Q)-11, where 1 denotes the vector (1,...,1)t.

Proof. See reference[20].

In this paper, we investigate ‖m‖∞, the ∞-norm of vector m. They are defined as ‖m‖∞=maxi∈T{mi}.

From these definitions, we could see that ‖m‖∞shows the maximum number of iteration steps for an algorithm to first hit the globally optimal solution(s).

3　Time Complexity Analysis of Hybrid Algorithm

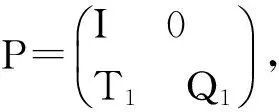
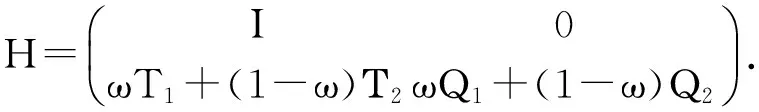
Proof. Suppose a solution is in state Si, then the hybrid algorithm could transit it from state Sito Sjeither by base algorithm 1 with probability ωpij, or by base algorithm 2 with probability (1-ω)mij, where pijand mijare entries of transition matrices P and M, respectively. So, the solution could be transited by the hybrid algorithm from state Sito Sjwith probability ωpij+ (1-ω)mij(i, j=1, 2, …, n), i.e., hij=(pij+(1-ω)mij. This means that H=ωP+(1-ω)M. By written in block form we obtain the proposition.

Let mi,hdenote the first hitting time of the hybrid algorithm when starting from state Si, and let mhdenote [mi,h]i∈T, where subscript T denote the transient states set. Let mi,1denote the first hitting time by base algorithm 1 when starting from state Si, and let m1denote [mi,1]i∈T; let mi,2the first hitting time by base algorithm 2 when starting from state Si, and let m2denote [mi,2]i∈T.

For a same combinatorial optimization problem, we have the following corollary on the first hitting time vector m1of base algorithm 1. Corollary 1. m1=(I-Q1)-11.

On the first hitting time vector m2of base algorithm 2, the corollary is

Corollary 2. m2=(I-Q2)-11.

For mhof the hybrid algorithm combining base algorithms 1 and 2, we have the following corollary.

Corollary 3. mh=(I-ωQ1-(1-ω)Q2)-11.

In the following, we investigate the ∞-norm of mh. The ∞-norm represents the worst case of the time complexity.

4　Relationship Between ‖mh‖∞ and ‖m1‖∞, ‖m2‖∞

In this section, we discuss the relationship between ‖mh‖∞and ‖m1‖∞,‖m2‖∞.

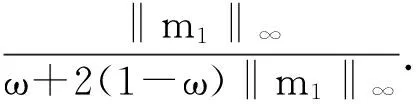
Proof. For a same combinatorial optimization problem, according to Corollary 1, we have m1=(I-Q1)-11, and according to corollary 3, we have mh=(I-ωQ1-(1-ω)Q2)-11. By transformation, we have (I-ωQ1-(1-ω)Q2)mh=1. Replacing tiem 1 in m1=(I-Q1)-11 by (I-ωQ1-(1-ω)Q2)mh, we have m1=(I-Q1)-1(I-ωQ1-(1-ω)Q2)mh.

So, we have m1=(I-Q1)-1(ω(I-Q1)+(1-ω)(I-Q2))mh. Further, m1=ωmh+(1-ω)(I-Q1)-1(I-Q2)mh.

By taking ∞-norms of both side of above equation, we have ‖m1‖∞=‖ωmh+(1-ω)(I-Q1)-1(I-Q2)mh‖∞, then ‖m1‖∞≤ω‖mh‖∞+(1-ω)‖(I-Q1)-1(I-Q2)mh‖∞, further, ‖m1‖∞≤ω‖mh‖∞+(1-ω)‖(I-Q1)-1‖∞‖(I-Q2)‖∞‖mh‖∞.

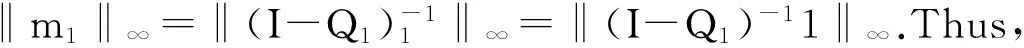
Since Q2is a block matrix of a transition matrix, ‖(I-Q2)‖∞≤2. Then, we have ‖m1‖∞≤ω‖mh‖∞+2(1-ω)‖m1‖∞‖mh‖∞. Further, ‖m1‖∞≤(ω+2(1-ω)‖m1‖∞)‖mh‖∞.

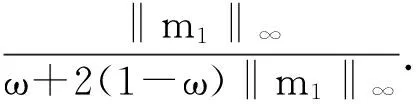
Proposition 2 demonstrates the relationship between mhand m1. The lower boundary may be trivial when ω takes a small value. For example, when ω=0, the lower boundary is 0.5. This is a trivial lower boundary. However, when ω takes a larger value, the lower boundary becomes nontrivial. For example, when ω1=1, the lower boundary is ‖m1‖∞, which is tight in this case.

In the same way, we get the relationship between mhand m2, that is Proposition 3.

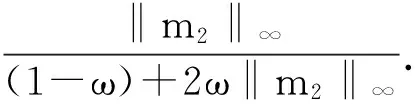
Proof. The proof is the same as that of Proposition 2.

This boundary may be trivial when ω takes a large value in [0, 1]. However, the smaller value ω takes, the tighter lower boundary becomes, since in this case base algorithm 1 takes a marginal role in the hybrid algorithm.

Propositions 2 and 3 demonstrate the lower boundaries of ‖mh‖∞. Both lower boundaries relate the norms of ‖m1‖∞and ‖m2‖∞. Since ‖V‖∞is the max item of vector V, Propositions 2 and 3 show the relationship between the maximum number of iteration steps of first hitting the globally optimal solution(s) for the hybrid algorithm and for the base algorithms.

Proof. It comes from combining Propositions 2 and 3.

This joint lower boundary is nontrivial when ω takes a large or small value. It tells us that the time complexity of the hybrid algorithm is not less than that of base algorithm 1 when ω is close to 1, and not less than that of base algorithm 2 when ω takes a value close to 0. Because when ω takes a value close to 0, base algorithm 1 becomes marginal in the hybrid algorithm, and when ω takes a value close to 1, base algorithm 2 becomes marginal in the hybrid algorithm. However, this joint lower boundary is trivial when ω takes a medium value in [0,1].

We have obtained the lower boundaries of ‖mh‖∞. Now we investigate the upper boundaries of ‖mh‖∞.

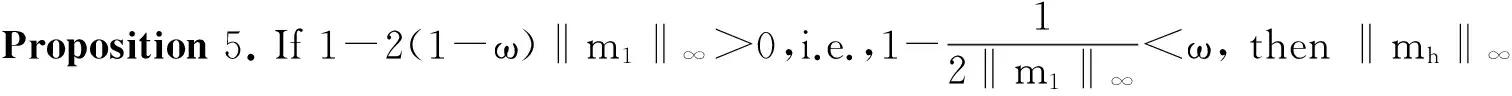
Proof. According to Corollary 1, we have m1=(I-Q1)-11. By transformation, we obtain (I-Q1)m1=1. According to Corollary 3, we have mh=(I-ωQ1-(1-ω)Q2)-11.

By replacing item 1 in the last equation with (I-Q1) m1, we obtain mh=(I-ωQ1-(1-ω)Q2)-1(I-Q1)m1, mh=(I-ωQ1-(1-ω)Q2)-1(I-ωQ1-(1-ω)Q2-(1-ω)Q1+(1-ω)Q2)m1, and mh= m1+(I-ωQ1-(1-ω)Q2)-1(-(1-ω)Q1+(1-ω)Q2)m1. By taking the ∞-norms of both sides, we have ‖mh‖∞≤‖m1‖∞+‖(I-ωQ1-(1-ω)Q2)-1(-(1-ω)Q1+(1-ω)Q2)m1‖∞and ‖mh‖∞≤‖m1‖∞+‖(1-ωQ1-(1-ω)Q2)-1‖∞‖(-(1-ω)Q1+(1-ω)Q2)m1‖∞.

Since the entries of (I-ωQ1-(1-ω)Q2)-1are non-negative, ‖mh‖∞=‖(I-ωQ1-(1-ω)Q2)-11‖∞=‖(I-ωQ1-(1-ω)Q2)-1‖∞.Hence, we have ‖mh‖∞≤‖m1‖∞+‖mh‖∞‖(-(1-ω)Q1+(1-ω)Q2)m1‖∞,‖mh‖∞≤‖m1‖∞+‖mh‖∞(‖-(1-ω)Q1‖∞+‖(1-ω)Q2‖∞)‖m1‖∞.and ‖mh‖∞≤‖m1‖∞+‖mh‖∞((1-ω)‖Q1‖∞+(1-ω)‖Q2‖∞)‖m1‖∞.

Since Q1and Q2are block matrices of a transition matrices, ‖Q1‖∞≤1 and ‖Q2‖∞≤1. Then, we have ‖mh‖∞≤‖m1‖∞+2(1-ω)‖mh‖∞‖m1‖∞, and‖mh‖∞(1-2(1-ω)‖m1‖∞)≤‖m1‖∞.

Proposition 5 gives an upper boundary of ‖mh‖∞. This upper boundary is related to ‖m1‖∞. It tells us that the time complexity of the hybrid algorithm is not larger than that of base algorithm 1 when ω takes a value close to 1. This upper boundary becomes tighter, when ω takes a value much closer to 0.

The following proposition gives another upper boundary of ‖mh‖∞, which is related to ‖m2‖∞.

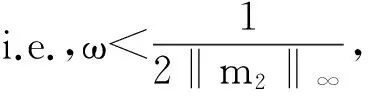
Proof. The proof is similar to that of Proposition 5.

This upper boundary is tight when ω takes a value close to 0. It tells us that if ω is close to 0, which means that base algorithm 1 takes a marginal role in the hybrid algorithm, the time complexity upper boundary of hybrid is not large than that of base algorithm 2.

The lower boundary and upper boundary of the hybrid algorithm are nontrivial when ω takes a value close to 0 or to 1.

When ω is close to 0, the time complexity of the hybrid algorithm is close to that of base algorithm 2. When ω is close to 1, the time complexity of the hybrid algorithm is close to that of base algorithm 1. This tells us that we should make the lowest time complexity algorithm take a notable role in such akind hybrid algorithm.

5　Conclusions and Furture Work

In this paper, we investigated the ∞-norm of mhof a kind of hybrid algorithms combining two base algorithms. We aim to study the relationship between ‖mh‖∞and ‖m1‖∞, ‖m2‖∞. In consequence, we obtained the lower and upper boundaries of ‖mh‖∞. The lower and upper boundaries of ‖mh‖∞of this kind of hybrid algorithms are functions of parameter ω and the corresponding norms of base algorithms. Those boundaries are nontrivial when ω is close to 0 or 1. This indicates that we should let the base algorithm that has a lower time complexity takes a major role in the hybrid algorithm, which may direct to design an efficient hybrid algorithm.

When ω takes a value not close to either 0 or 1, these boundaries may be trivial. Therefore, obtaining a tighter boundary is our future work. In addition, we will investigate the lower and upper boundaries of ‖mh‖1of this kind of hybrid algorithms which combining two base algorithms as shown in Hybrid Algorithms, which is an average case of the time complexity.

[1] Hendrickx I., Bosch A. V. D. Hybrid Algorithms with Instance-based Classification[C]. Proceedings of the 16th European Conference on Machine Learning, Lecture Notes in Computer Science, 2005，3720：158-169.

[2] Robles V., Pena J. M., Pérez M.S., Herves V. GA-EDA: A new hybrid cooperative search evolutionary algorithm[J]. In J. A. Lozano, P. Larranaga, I. Inza, and E. Bengoetxea, editors, Towards a New Evolutionary Computation. Advances in Estimation of Distribution Algorithms[M],Springer Verlag, 2006.

[4] Alba E., Chicano J. F. Training neural networks with GA hybrid algorithms[C]. Proceedings of the Genetic and Evolutionary Computation Conference, Alba E., Chicano J. F.GECCO 2004, ser. Lecture Notes in Computer Science, 2004,3102:852-863.

[5] Abraham A., Nath B. Optimal Design of Neural Nets Using Hybrid Algorithms[C]. Proceedings of 6th Pacific Rim International Conference on Artificial Intelligence (PRICAI 2000), 2000,1:510-520.

[6] Zhou Y., He J., Nie Q. A comparative runtime analysis of heuristic algorithms for satisfiability problems[J]. Artificial Intelligence, 2009, 173(2): 240-257.

[7] Yu Y., Zhou Z.-H. A new approach to estimating the expected first hitting time of evolutionary algorithms[J]. Artificial Intelligence, 2008, 172: 1809-1832.

[8] He J., Yao X. Drift analysis and average time complexity of evolutionary algorithms[J]. Artificial Intelligence, 2001, 127: 57-85.

[9] S. Droste, T. Jansen, I. Wegener. On the analysis of the (1+1) evolutionary algorithm. Theoretical Computer Science, 2002, 276: 51-81.

[10] Garnier J., Kallel L., Schoenauer M. Rigorous hitting times for binary mutations[J]. Evolutionary Computation, 1999, 7(2): 173-203.

[11] Sasaki G. H., Hajek B. The time complexity of maximum matching by simulated annealing[J]. Journal of the ACM, 1988, 35(2): 387-403.

[12] He J., Yao X. Towards an analytic framework for analysing the computation time of evolutionary algorithms[J]. Artificial Intelligence, 2003, 145:59-97.

[13] Lehre P. K., Yao X. On the Impact of Mutation-Selection Balance on the Runtime of Evolutionary Algorithms[J]. IEEE Transactions on Evolutionary Computation,2012,16(2):225-241.

[14] Chen T., Tang K., Chen G., Yao X. A Large Population Size Can Be Unhelpful in Evolutionary Algorithms[J]. Theoretical Computer Science,2012,436:54-70.[15] Lehre P. K., Yao X. Crossover can be constructive when computing unique inputoutput sequences[J]. Soft Computing, 2011, 15(9):1675-1687.

[16] Chen T., He J., Chen G., and Yao X. Choosing selection pressure for wide-gap problems[J]. Theoretical Computer Science, 2010, 411(6): 926-934.

[17] Clerc M., Kennedy J. The particle swarm: explosion stability and convergence in a multi-dimensional complex space[J]. IEEE Transactions Evolutionary Computation,2002, 6(1): 58-73.

[18] Trelea I. C. The particle swarm optimization algorithm: convergence analysis and parameter selection[J]. Information Processing Letters, 2003, 85: 317-325.

[19] Bergh V. D., Engelbrecht A.P. A convergence proof for the particle swarm optimizer[J]. Fundamental Informaticae, 2010, 105: 341-374.

[20] Iosifescu M. Finite Markov Processes and Their Applications[M]. Chichester: Wiley, 1980.

[21] Gentle J. E. Matrix Algebra: Theory, Computations, and Applications in Statistics[M]. Berlin German: Springer, 2007.