数学形态学分形维数广义估算方法及其应用
2014-04-02李洪儒许葆华
王 冰, 李洪儒, 许葆华
(军械工程学院导弹工程系, 河北 石家庄 050003)
引 言
滚动轴承是旋转机械中的关键性元件,由于长期受到载荷、安装、润滑状态等因素的影响,轴承极易受到损伤,进而影响整个机械设备的性能。因此,轴承一直都是设备状态监测与故障诊断领域的热门研究对象[1]。
随着维修理论的发展,基于状态的维修越来越得到人们关注。故障预测技术是实现基于状态维修的关键。主要包括三个方面:运行状态的特征提取;退化状态识别;故障预测[2,3]。其中,运行状态特征提取是实现退化状态识别和故障预测的基础,直接影响退化状态识别的准确性和故障预测的可信性[4]。其着眼点在于特征信息对设备性能退化程度的量化反应能力,而非对不同故障模式的区分能力。文献[4,5]提取并选取小波相关特征尺度熵作为预测特征指标;文献[6,7]以小波包分解后的节点能量作为特征向量,定量评估样本的退化程度;文献[8]将通过循环平稳分析得到的组合切片累积能量作为预测特征值,均取得了较好的效果。
滚动轴承故障振动信号是一种典型的非平稳、非线性信号。分形维数则可以定量描述其复杂性和非线性。常见的分形维数有关联维数、盒维数、信息维数等,其中,盒维数应用最为广泛[9]。但由于现有的盒维数估计方法不准确[10],文献[11]提出一种基于数学形态学的分形维数计算方法,该方法计算量小,计算结果稳定且准确,已在轴承故障诊断领域得到了有效的应用[12,13]。
本文在基于数学形态学的分形维数计算方法基础上,提出三种形态学分形维数广义估算方法,以FBM仿真信号为例对其准确性和适用性进行分析。以此为基础,提出基于数学形态分形维数与灰色关联分析的退化状态识别方法。并采用实测数据对该方法进行验证。
1 基于数学形态学的分形维数计算方法
分形维数可以定量描述分形对象的复杂程度。在各种分形维数中,盒维数的应用最为广泛。然而盒维数的计算过程由于对信号进行规则的网格划分,因此影响了估算的精度[10]。针对此问题,文献[11]提出一种基于数学形态学的分形维数估计方法。具体过程如下。
假设离散时间信号为f(n),n=1,2,…,N,单位结构元素为g,则在尺度ε下所使用的结构元素定义为[14]
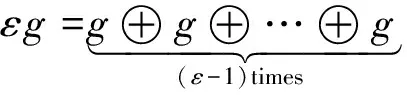
(1)
定义尺度ε对信号的覆盖面积为
(2)
根据文献[6]证明,覆盖面积满足如下条件
(3)
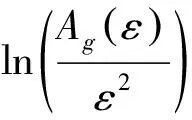
2 数学形态学的分形维数广义估算方法
2.1 基于数学形态学的分形维数广义估算方法
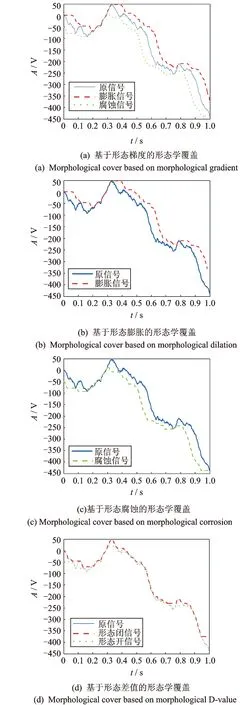
从几何意义上分析,在上述方法中,由式(2)所定义的形态学覆盖面积是为信号f(n)以结构元素εg进行膨胀和腐蚀运算后的差分,即形态梯度,本文称该方法为基于形态梯度的形态覆盖定义方法。为了分析其他形态学算子在形态学覆盖定义中的有效性,本文提出3种形态学覆盖广义定义,其表达式如下:
(4)
(5)
(6)
根据覆盖面积的定义方式,式(4)~(6)分别定义为基于形态膨胀、形态腐蚀和形态差值的形态学覆盖。
以形态学覆盖面积的广义定义为基础,通过最小二乘线性拟合即可得到对信号分形维数的广义估计。
2.2 仿真分析
为了验证三种形态学覆盖广义定义在计算中的有效性,采用FBM信号进行仿真分析。分数布朗运动(FBM)是描述时间(或空间)长程相关、功率谱满足指数规律、增量服从正态分布的非平稳随机过程的数学模型之一,是用来描述自然界随机分形一种常用的分形模型,满足如下定义[15]
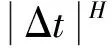
(7)
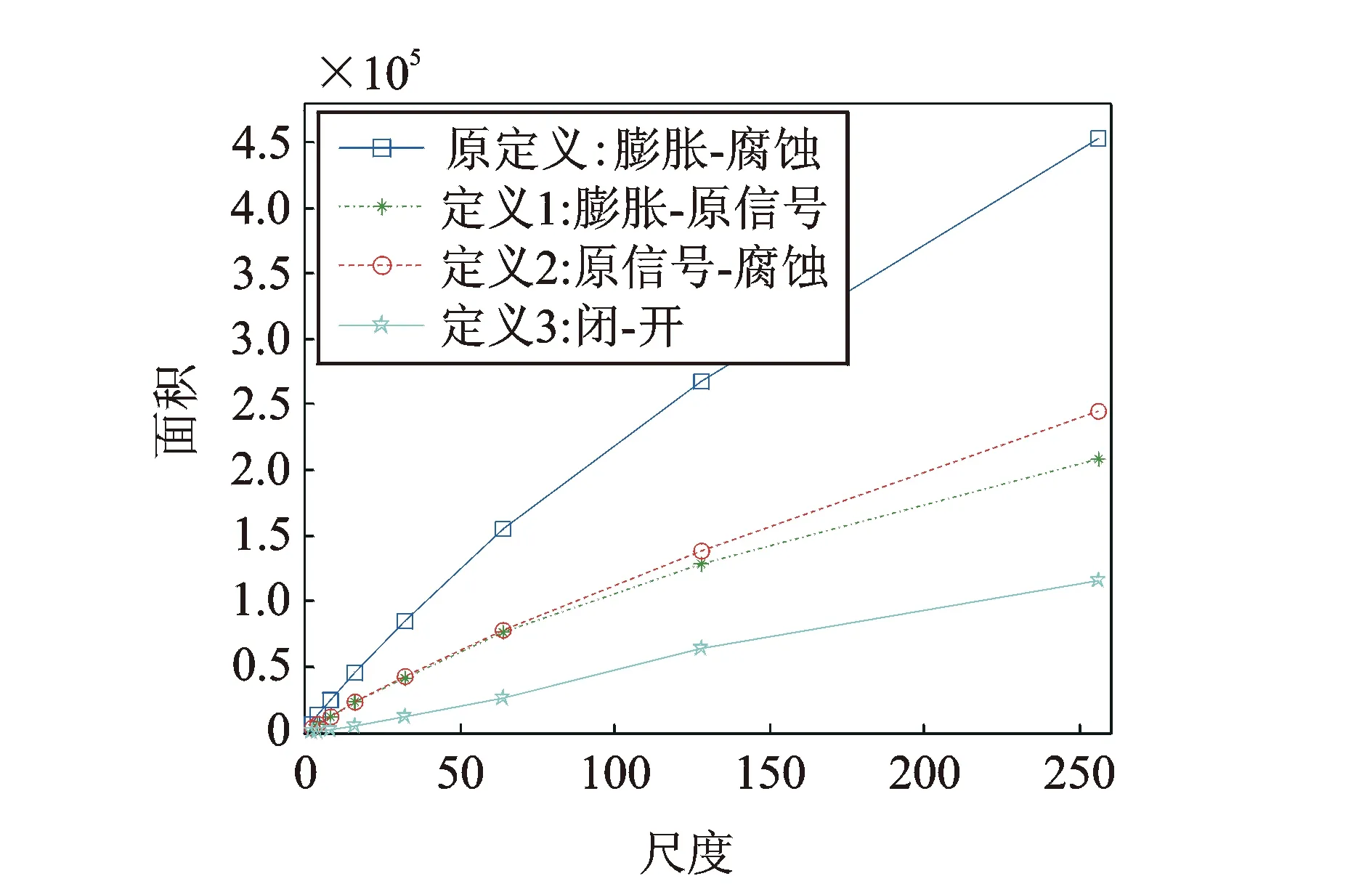
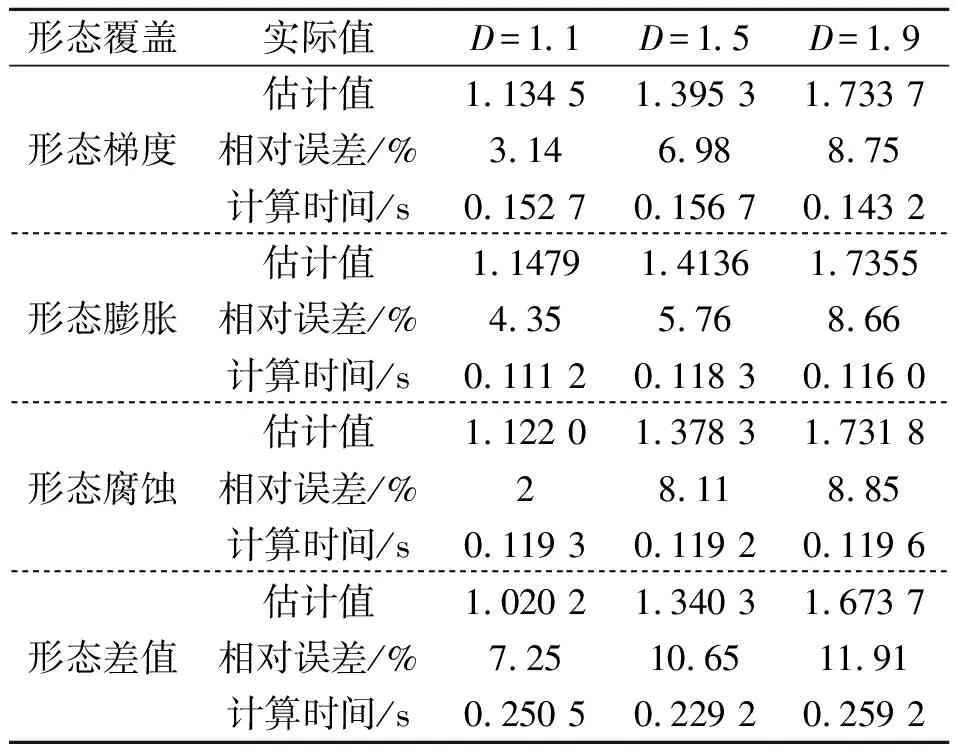
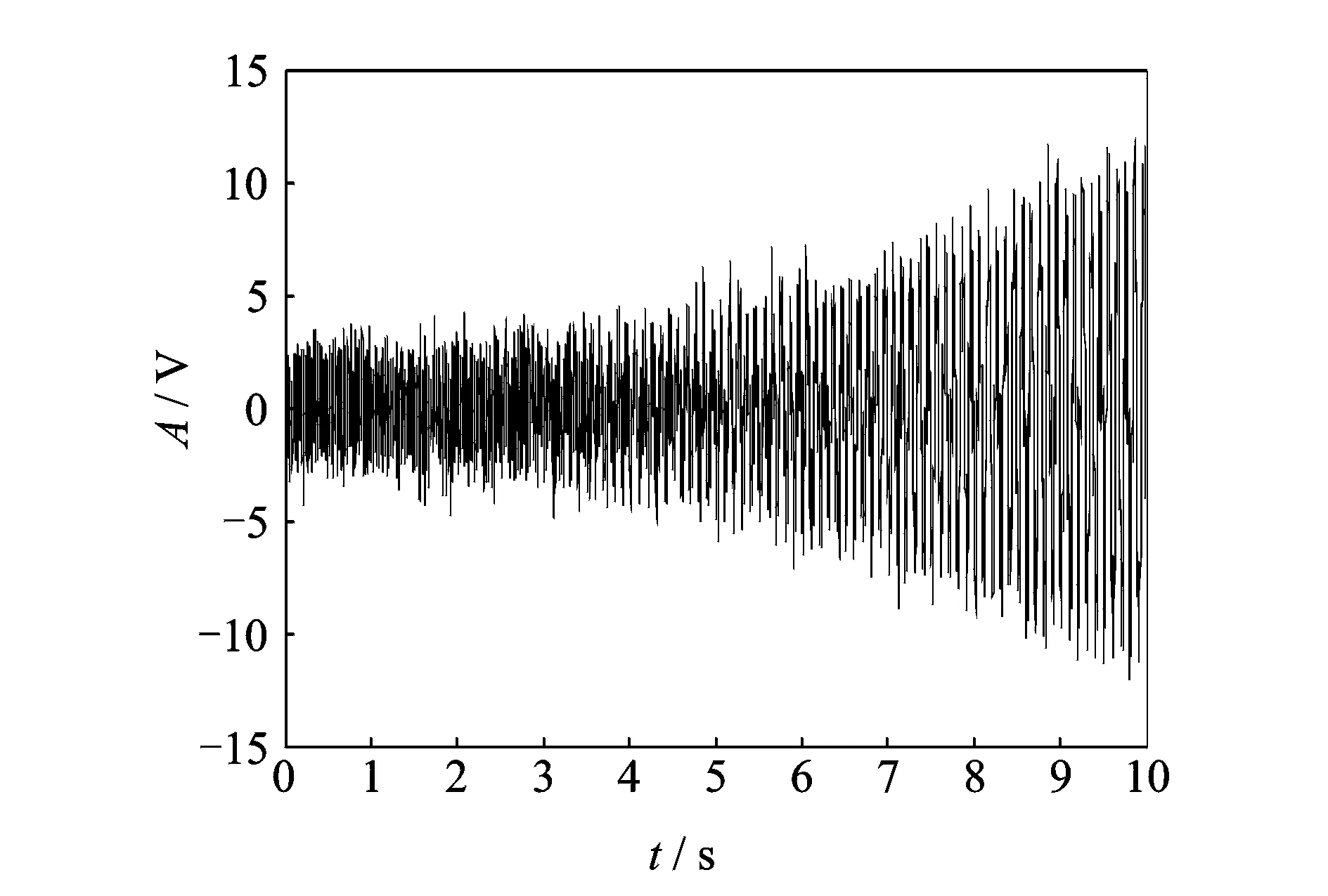
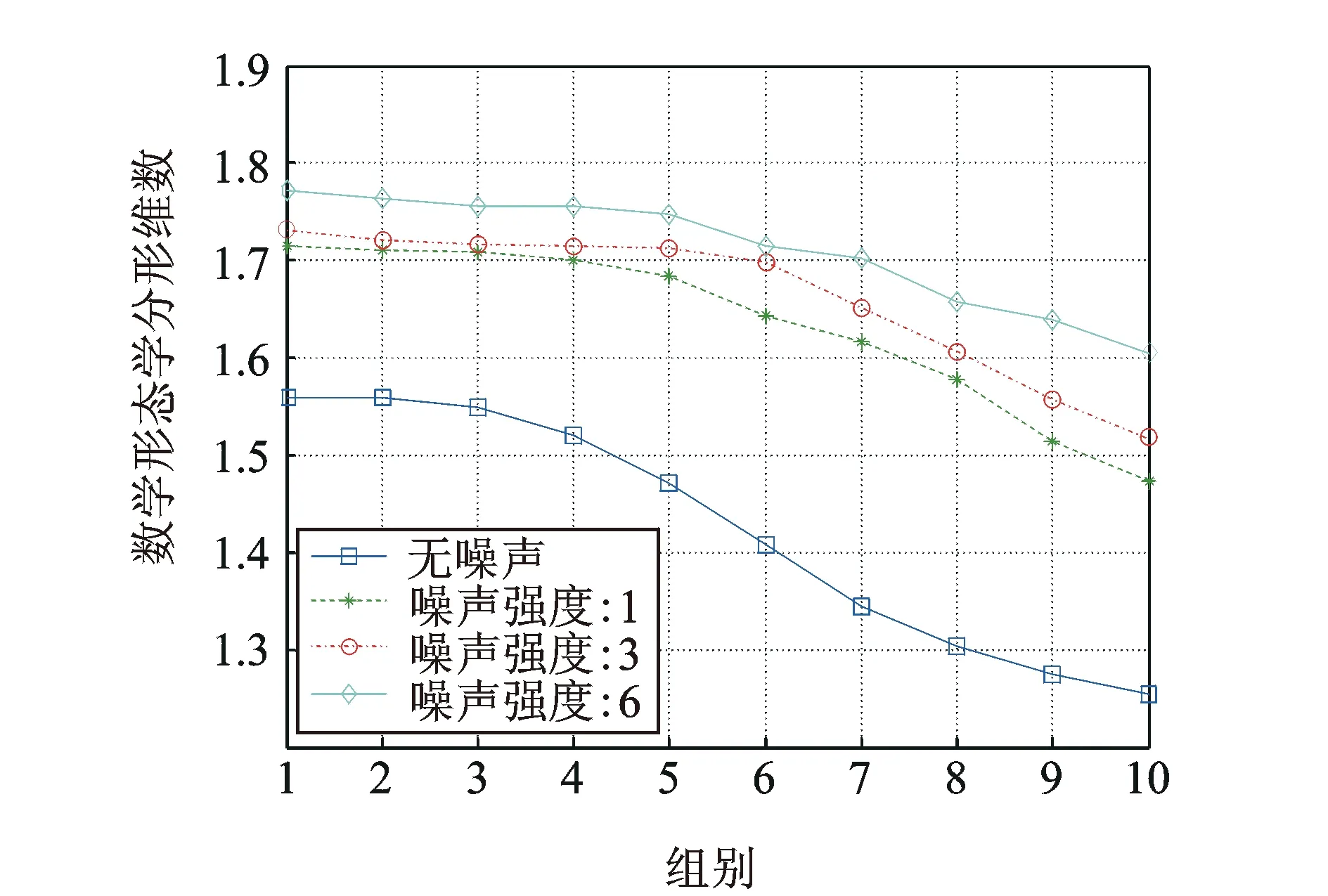
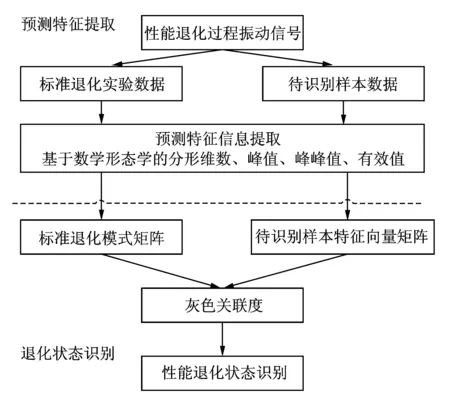
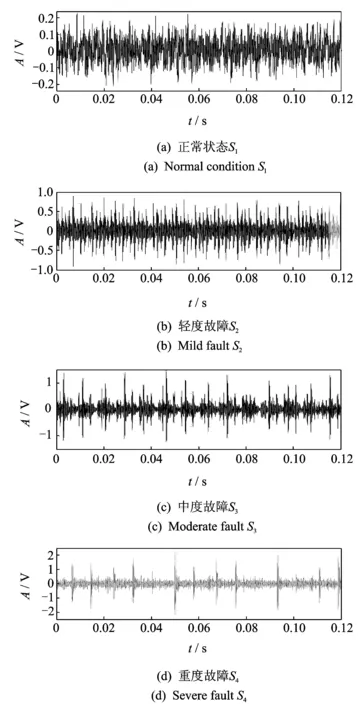
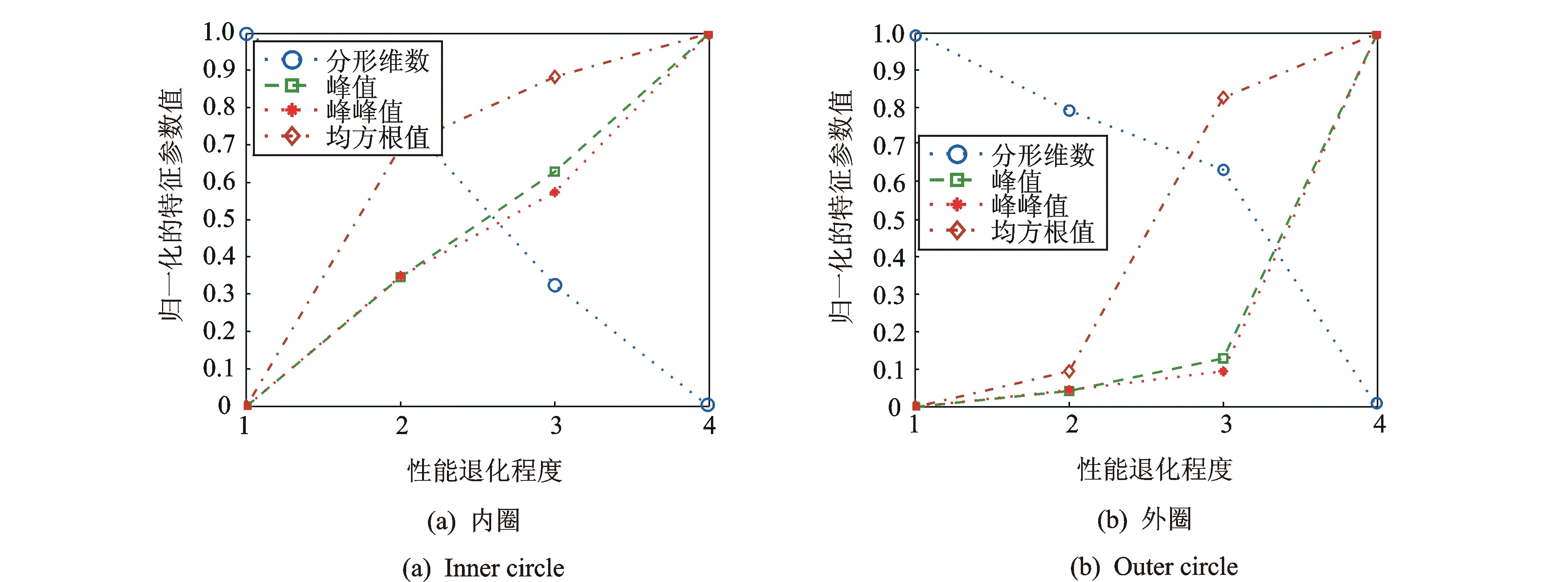
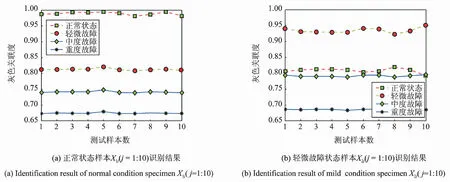
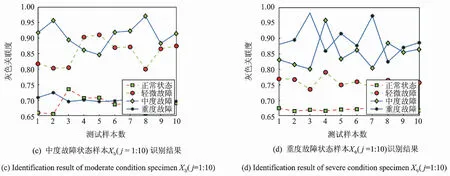
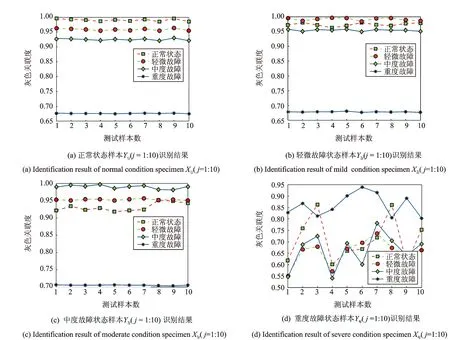
式中k为常量,ξ为标准高斯随机过程。H(0 本文采用分形工具箱Fraclab中的函数fbmlevinson来生成BH(t)[16],采样频率为f=2 048 Hz,采样点数为N=2 048,图1显示了3种不同维数(D=1.1,1.5,1.9)下的FBM分形信号。 图1 不同分形维数下的FBM时域波形 分别根据原定义和3种广义估算方法计算FBM信号分形维数。选择扁平结构元素g=[0,0,0],尺度进行离散化设置,取值为[2,4,8,16,32,64,128,256]。 图2对比了在4种形态学覆盖的定义下,对D=1.1的FBM信号进行尺度为64时的形态学覆盖结果。在图2(a)所示的原定义中,形态学覆盖为膨胀和腐蚀之间所包含的区域,而其上覆盖和下覆盖分别为图2(b)和(c)所描述的基于形态膨胀和形态腐蚀的形态学覆盖。对比分析同一尺度下的形态学覆盖面积大小,图2(a)覆盖最大,图2(b)和(c)次之,图2(d)中所定义的形态差值覆盖最小。 图2 尺度为64时的不同定义下的形态学覆盖 图3描述了形态学覆盖面积与结构元素尺度的变化关系。可以看出,尺度越大,形态学覆盖面积越大。4种方法相比,基于形态梯度的原定义覆盖面积最大,分析其原因,基于形态膨胀和形态腐蚀的定义分别用上覆盖和下覆盖代替原有覆盖,导致覆盖面积减小。基于形态差值的定义采用形态闭和开运算,运算量加倍,覆盖面积最小。 图3 不同离散尺度下形态学覆盖面积变化趋势图 由于分形维数是通过对覆盖面积和尺度的最小二乘线性拟合而计算出的,因此形态覆盖面积的变化趋势影响着算法的有效性。从图3可以看出,4种曲线具有近似的变化趋势,从定性上分析,3种广义估算方法是可行的。下面将进行定量对比分析。 表1为4种定义方法对FBM信号分形维数的定量估计值和相对误差。实验所采用计算机配置为Intel(R) Core i5-2400 CPU @3.10 GHz,内存为4 GB,软件为Matlab R2010b。 表1 FBM信号的分形维数估计 可以看出,基于形态差值的定义方法计算结果明显偏低,误差较大,耗时较长。而基于形态膨胀和形态腐蚀的方法与原算法相比,计算精度相当,误差均较低。并且由于单次运算只进行一次腐蚀或膨胀操作,计算量减半,运算速度更快。 综上分析,基于形态膨胀和形态腐蚀的分形维数广义估算方法在运算精度方面与原算法相当,运算速度更快,可以在实际中替代原算法。基于形态差值的分形维数广义估算方法效率精度较低,运算速度较慢,不适合实际运用。 如何选取能够表征轴承性能退化程度的特征指标,是对轴承进行性能退化状态识别的基础。所选取的特征指标应具有良好的稳定性和关联性。稳定性是指该指标应对工况变化以及环境噪声具有很强的抗干扰能力;关联性是指该指标的变化趋势应与设备的性能退化过程具有相关联,随性能的退化表现出单调性的变化趋势。 从轴承振动信号的本质分析,其信号在全寿命周期中的变化过程,就是其内部随机成分所占比例不断变化的过程。因此,提出基于数学形态学分形维数的特征提取方法,用可以表征分形对象复杂度的分形维数表征轴承的性能退化程度。 为了该方法的有效性,采用仿真信号进行分析[17] (8) 式中 0.1t2cos(2π×10t+2)为故障模拟信号,cos(2π×50t)为常规振动信号,n(t)代表高斯噪声,幅值0.1t2用来近似反映故障随时间的变化过程。信号采样点数为N=10 240,采样频率为1 024 Hz。为了研究白噪声的影响,分别设定3种噪声强度1,3,6,图4显示了噪声强度为1时的仿真信号时域波形。 图4 仿真信号时域波形 将信号等分为10段并顺序标记,用10组数据近似描述仿真信号故障程度不断加深的性能退化过程。采用基于形态膨胀的数学形态学分形维数计算方法计算每一组数据的分形维数。选择扁平型单位结构元素g=[0,0,0],尺度为[2,4,8,16,32,64,128,256],不同噪声强度下的仿真信号分形维数变化趋势如图5所示。 图5 不同噪声强度下分形维数变化趋势图 可以看出,随着故障程度的不断加深,基于数学形态学的分形维数数值不断减小,其值在区间[1.2,1.58]内变化,呈现出递减的趋势。且在故障初期变化缓慢,分析认为这与仿真信号以0.1t2进行幅值变化紧密相关。另外,随着噪声强度的不断加强,其中,当噪声强度为1时,分形维数的数值在区间[1.48,1.72]内变化,噪声强度为6时,其数值在区间[1.6,1.78]范围内变化,可见,噪声强度越大,形态分形维数的计算结果越大,但从整体而言,依然保持递减趋势。综上分析,基于数学形态学的分形维数与性能退化过程具有较好的关联性,并且对噪声具有一定的抗干扰能力。 为了增强预测特征向量的完备性,本文另选取已在文献[18]中验证的峰值、峰峰值、有效值3个故障预测特征参数,以此构成对电机轴承性能退化状态识别的四维预测特征向量。 性能退化状态识别是一种多类分类问题,与故障模式识别侧重于对多故障类型分类不同,性能退化状态识别更强调对性能退化状态的分类。灰色关联分析是灰色系统理论进行系统分析的重要方法,它是根据系统各个因素之间的内部联系或发展态势的相似程度来度量因素之间关联度的方法[14]。本节在前文基础上提出基于分形维数和灰色关联分析的轴承性能退化状态识别方法。其步骤如图6所示。 图6 基于分形维数和灰色关联分析的轴承退化状态识别流程图 首先确定样本对象,将性能退化过程振动信号分为标准退化实验样本数据和待识别样本实验数据。之后按照性能退化的程度将性能退化过程分为n个退化状态,分别提取每个退化状态下的特征向量,并对结果进行归一化处理。特征向量记为F={F1,F2,…,Fi},其中i为向量中特征参数的个数。本文取i=4。在此基础上,建立标准退化模式矩阵和待识别样本特征向量矩阵。计算待识别样本特征向量与标准模式退化模式矩阵的灰色关联度,关联度最大值即为待识别样本的性能退化状态。 为验证本文所提方法在电机滚动轴承性能退化状态识别中的有效性,采用美国凯斯西储大学电气工程实验室的滚动轴承振动加速度实验数据进行实例分析[19]。测试轴承为SKF6205-2RS深沟球轴承,采样频率为48 kHz。转速为1 730 r/min,载荷为2.25 kW。以4种不同故障程度的轴承内圈和外圈振动信号近似模拟内外圈由正常状态逐渐经历一系列不同的退化状态直至完全失效的这一性能退化过程。故障程度通过轴承内外圈点蚀的直径来描述。分别以直径0,0.18,0.36,0.54 mm的点蚀故障模拟轴承内外圈正常状态、轻度故障、中度故障、重度故障4种工作状态。 选取轴承内外圈在4种工作状态下的振动加速度数据,数据长度为6 000,分别记为Si(i=1,…,4),Ti(i=1,…,4),其中i为轴承工作状态序号,以此作为轴承内外圈标准性能退化实验数据;另外选取内外圈在4种工作状态下长度为1 000的振动加速度数据,分别记为Xij(i=1,…,4;j=1,…,10),Yij(i=1,…,4;j=1,…,10),其中i为轴承工作状态序号,j为待识别样本序号,以此作为轴承内圈和外圈的待识别样本数据。 图7 滚动轴承内圈在4种工作状态下振动信号时域波形 图7为轴承内圈在4种工作状态下的振动加速度数据Si的原始时域波形。由图中可以明显看出,4种状态下的轴承振动信号在时域结构上具有较为明显的差异。正常信号呈现出几乎随机性的分布,随着内圈故障程度的不断加深,信号的规律性明显增强,幅值也不断增大。 采用3.1节提出的特征提取方法,分别计算标准性能退化实验数据(Si,Ti)和待识别样本数据(Xij,Yij)的特征向量,建立标准退化模式矩阵和待识别样本特征向量矩阵。图8(a)和(b)分别为经归一化处理后的轴承内外圈标准性能退化实验数据特征参数。其中,横坐标代表不同的性能退化程度,序号1,2,3,4分别代表轴承内外圈正常状态、轻度故障、中度故障、重度故障4种工作状态。 可以看出,随着轴承内外圈的故障程度的不断加深,4个特征参量均发生明显的关联性变化,分形 图8 轴承内外圈标准性能退化实验数据特征参数 维数随着故障退化程度的加深而不断减小,峰值、峰峰值和有效值随着故障退化程度的加深而不断增加。且分形维数的分布更加平均,区分效果更好,有效值的效果次之,峰值和峰峰值对轻度和重度故障的区分效果不明显。 根据特征提取结果,分别建立轴承内外圈的标准退化模式矩阵Fin和Fout,轴承内外圈待识别样本特征向量矩阵Aij(i=1,…,4;j=1,…,10),Bij(i=1,…,4;j=1,…,10),其中i为实际轴承工作状态序号,j为待识别样本序号。 分别计算Aij与Fin,Bij与Fout的灰色关联度,分辨系数ρ=0.5。根据灰色关联度的大小识别待识别样本的性能退化状态。图9(a)~(d)显示了不同内圈退化状态样本的识别结果。可以看出,除中度和重度故障状态测试样本中各有2个未被正确识别外,其余各个样本均可被正确识别。其总体状态识别成功率达到90%;在图10(a)~(d)所显示的轴承外圈故障性能退化状态识别结果中,除重度故障状态测试样本有2个样本未被正确识别外,其余各个样本均被正确的识别。其总体状态识别成功率达到95%。由此可见,在轴承内外圈性能退化状态识别中,基于数学形态学分形维数与灰色关联分析的方法可以达到较高的识别率,效果理想。 图9 轴承内圈测试样本Xij退化状态识别结果 图10 轴承外圈测试样本Yij退化状态识别结果 (1)基于形态膨胀、形态腐蚀、形态差值的分形维数广义估算方法是从形态覆盖的角度对原有算法的广义扩展。通过仿真实验可以看出,基于形态膨胀、形态腐蚀的估算方法在精确度和运算速度方面均具有一定的优势,而基于形态差值的估算方法则运算量大,精确度较之其他方法也略低。 (2)基于形态分形维数与灰色关联分析的性能退化状态识别方法将形态学分形维数引入到预测特征提取中,在仿真和实例数据的分析处理中取得了较为理想的效果。 (3)机械设备在实际运行中的性能退化过程要复杂得多,需要考虑转速、载荷及环境因素时变性带来的影响,且不易采集。采用不同损伤程度实验数据是一种用离散近似模拟连续的方法,必然有一定的局限性。 参考文献: [1] Patil M S,Mathew J,Rajendra Kumar P K. Bearing signature analysis as a medium for fault detection: a review[J].Journal of Tribology,2008,130(1) : 1—7. [2] QIU H, LEE J, LIN J, et al. Robust performance degradation assessment methods for enhanced rolling element bearing prognostics[J]. Advanced Engineering Informatics, 2003, 17: 127—140. [3] ZHANG X D, XU R, KWAN C, et al. An integrated approach to bearing fault diagnostics and prognostics[A].2005 American Control Conference[C].Portland, 2005: 2 750—2 755. [4] 曾庆虎,邱静,刘冠军. 基于小波相关特征尺度熵的HSMM设备退化状态识别与故障预测方法[J]. 仪器仪表学报,2008,12(29):2 559—2 564.ZENG Qing-hu, QIU Jing, LIU Guan-jun. Equipment degradation state recognition and fault prognosis method based on wavelet correlation feature scale entropy and HSMM[J]. Chinese Journal of Scientific Instrument,2008,12(29):2 559—2 564. [5] 曾庆虎,邱静,刘冠军. 基于HSMM的机械故障演化规律分析建模与预测[J]. 机械强度,2010,32(5):695—701.ZENG Qing-hu, QIU Jing, LIU Guan-jun. Modeling and prognostics of mechanical fault based on HSMM[J]. Journal of Mechanical Strength,2010,32(5):695—701. [6] 肖文斌,陈进,周宇,等. 小波包变换和隐马尔可夫模型在轴承性能退化评估中的应用[J]. 振动与冲击,2011,30(8):32—35.XIAO Wen-bin, CHEN Jin, ZHOU Yu,et al. Wavelet packet transform and hidden Markov model based bearing performance degradation assessment[J]. Journal of Vibration and Shock,2011,30(8):32—35. [7] 潘玉娜,陈进. 小波包-支持向量数据描述在轴承性能退化评估中的应用研究[J]. 振动与冲击,2009,28(4):164—167.PAN Yu-na, CHEN Jin. Wavelet package-support vector data description applied in bearing performance degradation assessment[J]. Journal of Vibration and Shock, 2009,28(4):164—167. [8] 潘玉娜,陈进. 结合循环平稳和支持向量数据描述的轴承性能退化评估研究[J]. 机械科学与技术,2009,28(4):442—445.PAN Yu-na, CHEN Jin. Assessment of bearing performance degradation by cyclostationarity analysis and support vector data description[J]. Mechanical Science and Technology for Aerospace Engineering, 2009,28(4):442—445. [9] 訾艳阳,胥永刚,何正嘉.离散振动信号分形盒维数的改进算法和应用[J].机械科学与技术, 2001, (03): 373—376.ZI Yan-yang, XU Yong-gang, HE Zheng-jia, Application and improved algorithm of fractal box dimension for disperse vibration signal[J]. Mechanical Science and Technology, 2001,(03): 373—376. [10] Chaudhuri B B, Sarkar N. Texture segmentation using fractal dimension[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1995. 17(1):72—77. [11] Maragos P, Sun F K. Measuring the fractal dimension of signals: morphological covers and iterative optimization[J].IEEE Transactions on Signal Processing, 1993,41(1): 108—121. [12] 李兵,张培林,任国全,等. 基于数学形态学的分形维数计算及在轴承故障诊断中的应用[J]. 振动与冲击,2010,29(5):191—194.LI Bing, ZHANG Pei-lin, REN Guo-quan, et al. Mathematic morphology-based fractal dimension calculation and its application in fault diagnosis of roller bearings[J]. Journal of Vibration and Shock, 2010,29(5):191—194. [13] 李兵,张培林,米双山,等. 齿轮故障信号多重分形维数的形态学计算方法[J]. 振动、测试与诊断, 2011,31(4):450—453.LI Bing, ZHANG Pei-lin, MI Shuang-shan,et al. Mathematical morphology based on multifractal dimensions for gear fault diagnosis[J]. Journal of Vibration, Measurement & Diagnosis,2011,4(31):450—453. [14] 沈路,周晓军,张文斌,等.基于形态滤波与灰色关联度的滚动轴承故障诊断[J].振动与冲击. 2009,28(11):17—20.SHEN Lu, ZHOU Xiao-jun, ZHANG Wen-bin, et al. Fault diagnosis of rolling elem ent bearing based on morphological filter and grey incidence[J]. Journal of Vibration and Shock. 2009,28(11):17—20. [15] 朱波华. 基于分形理论的信号处理与分析的研究[D]. 武汉:武汉理工大学,2008.ZHU Bo-hua. Research on signal process and analysis based on fractal theory [D].Wuhan : Wuhan University of Technology, 2008. [16] Fraclab: A fractal analysis toolbox for signal and image processing[EB/OL]. http://fraclab.saclay.inria.fr/, 2009. [17] 徐东,徐永成,陈循,等. 基于EMD的灰色模型的疲劳剩余寿命预测方法研究[J]. 振动工程学报,2011,24(1):104—110.XU Dong, Xu Yong-cheng, CHEN Xun, et al. Residual fatigue life prediction based on grey model and EMD[J]. Journal of Vibration Engineering, 2011,24(1):104—110. [18] 潘玉娜.滚动轴承的性能退化特征提取及评估方法研究[D]. 上海:上海交通大学,2011.PAN Yu-na. Study on feature extraction and assessment method of rolling element bearing performance degradation[D]. Shanghai: Shanghai Jiao Tong University,2011. [19] Kenneth A Loparo.Bearing data center [EB/OL].Case western reserve university , 2000[2010-03-26] . http://www.eecs.case.edu/laboratory/bearing/welcome_overview.htm.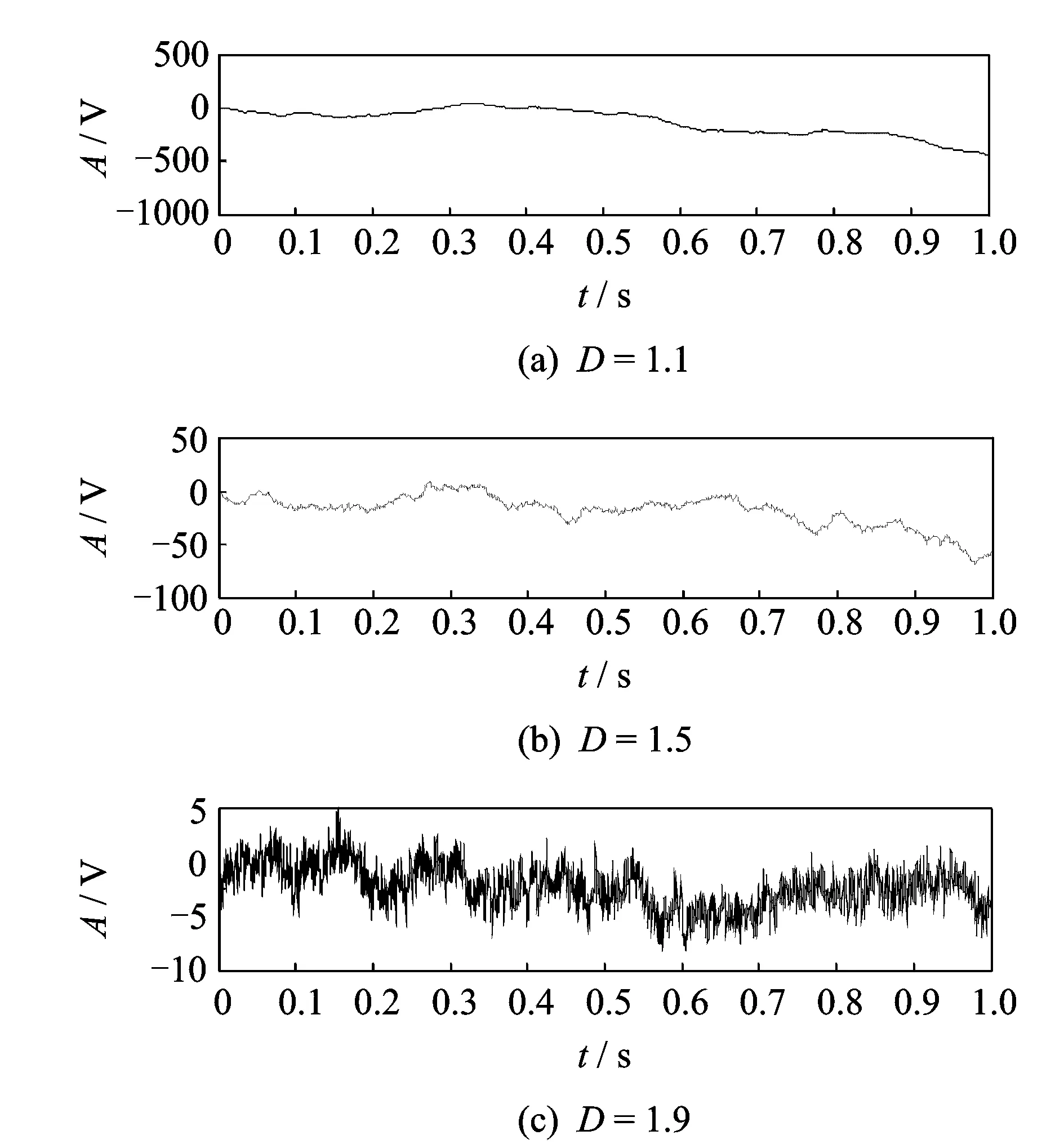
3 基于分形维数和灰色关联分析的轴承退化状态识别
3.1 基于数学形态学分形维数的特征提取
3.2 性能退化状态识别
4 实验数据验证
4.1 特征提取
4.2 灰色关联分析与退化状态识别
5 结 论
