舵结构系统的飞行自激振动特性

王成华， 及红娟， 童轶男

(北京航天长征飞行器研究所，北京 100076)

引 言

间隙和干摩擦等环节的存在使舵结构系统的非线性问题突出，产生一些有别于线性系统的特殊振动现象，改变了系统原有的频响特性，使系统的工作品质和效率下降、使飞行器的动力学环境恶化，给控制系统和伺服系统的设计乃至设备的环境适应性设计都带来困难。文献[1]已就舵结构系统的非线性动力学问题，基于理论分析进行了一定程度研究，但分析工作仅局限于结构系统自身，未涉及舵面非定常气动力对系统响应的影响，因此对于在飞行中发生的一些特殊振动现象仍不能给出合理确切的解释。本文基于文献[1]工作基础，将舵面非定常气动阻尼效应引入舵结构系统的振动响应分析中，进一步研究了飞行器在低动压或稀薄大气中飞行时所经历的一类特殊自激振动现象。基于本文方法与认识，飞行中舵面的非定常气动载荷——特别是俯仰阻尼力矩，会影响自激振动的发生和发展过程。因此首先借助当地流活塞理论[2，3]，确定出舵面气动俯仰阻尼力矩沿弹道的变化情况，将俯仰阻尼力矩作为附加粘性阻尼项引入系统；忽略高次谐波项，采用等价线性化方法研究了舵结构系统发生自激振动的机理和振动的响应特性[4，5]；通过数值积分模拟了舵结构系统倍周期自激振动的各次谐波解，得到了与飞行试验遥测结果相一致的现象和规律。

1 舵结构系统非线性振动力学模型

1.1 舵结构系统的主要动力学特征参数

舵结构系统典型结构形式和受力情况如图1所示。舵轴通过轴承安装固定于支撑舱段上；伺服系统作动器一端与支撑舱段铰连，一端通过作动器连杆推动摇臂、带动舵面相对支撑舱段偏转。舵结构系统固有频率ω0决定于舵系统的转动惯量Jδ及其扭转刚度kδ。阻尼则包括两部分：由轴承润滑和结构产生可作为粘性阻尼(Viscous Damping)考虑的线性部分，本文用阻尼系数c1表示；以及干摩擦(Coulomb Friction)或类似非线性阻尼部分，伺服系统和舵结构系统各传动环节均可产生此类阻尼[6～9]，本文用符号fc表示。舵结构系统不可避免会存在间隙，间隙量大小本文用2e表示。飞行中舵面会受气动载荷作用，包括静载荷和非定常载荷，非定常载荷对舵系统响应的影响不可忽视，影响程度则决定于舵面形状和来流参数如马赫数、攻角、飞行动压等。

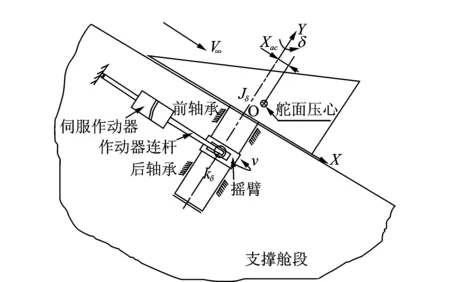
图1 舵结构系统形式和动力学描述示意图

1.2 舵结构系统的非线性振动模型

不失一般性，考虑扭转刚度低于弯曲刚度情况。在控制和伺服系统作用下，舵面相对支撑舱段发生偏转、令偏转角速度为v，建立图2所示非线性振动力学模型，其中：干摩擦环节施加在舵和支撑舱段之间，以体现干摩擦力矩产生的真实状态；间隙施加在舵轴和作动器之间，只当舵轴运动首先“吃掉”间隙后，舵轴刚度才起作用。

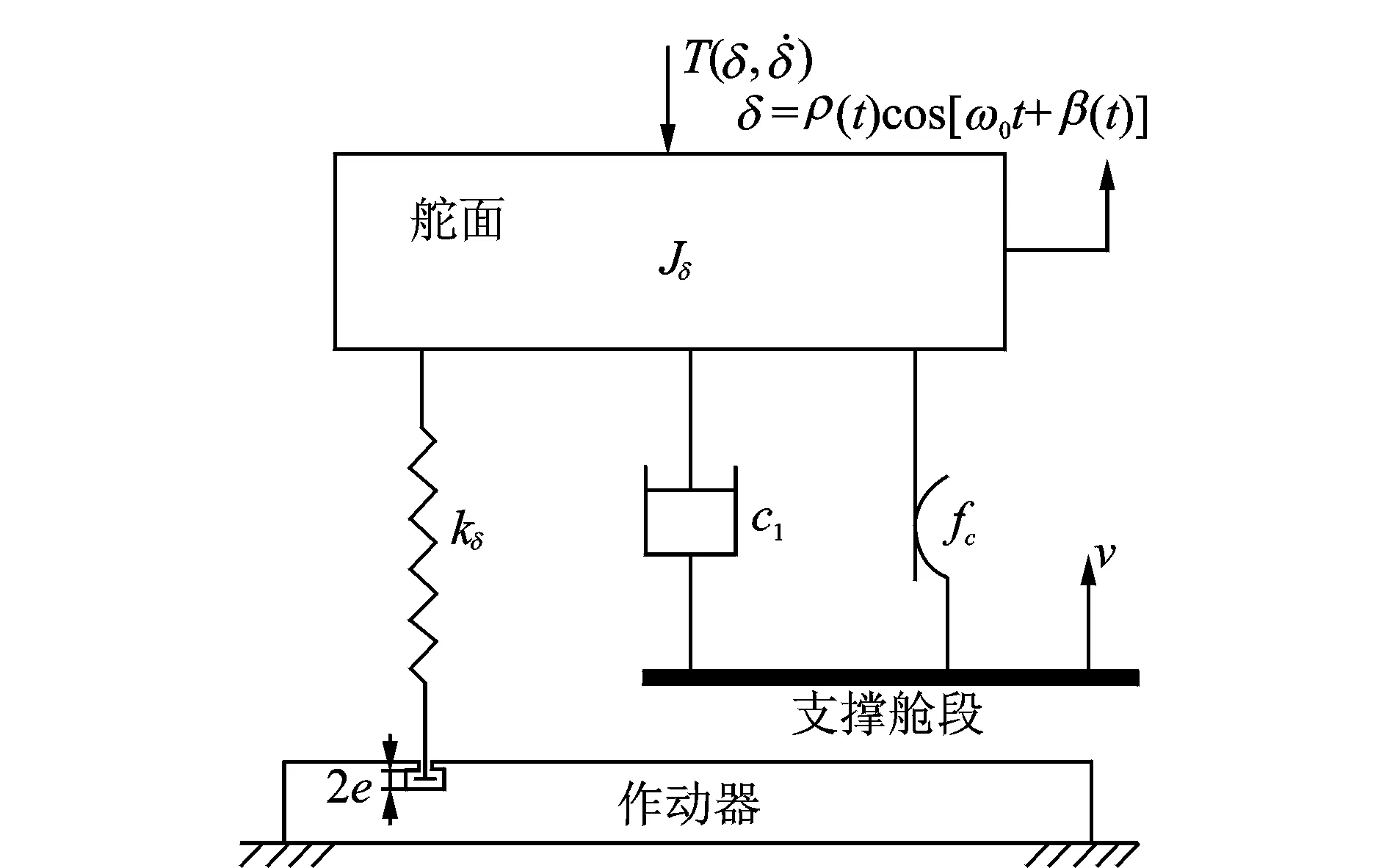
图2 飞行状态舵结构系统振动力学模型

坐标系固连于作动器，建立舵结构系统扭转振动方程

(1)

式中右端项代表舵面非定常气动力矩，fk(δ,e)代表间隙诱导弹性力矩损失附加项，表达式为

(2)

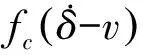
(3)

式中 sgn()表示符号函数；k1，k3为动摩擦力矩曲线方程系数，具体形式如下

(4)

1.3 舵面非定常气动力矩

舵面绕舵轴微幅振动时，图1所示坐标系下舵面中性面挠度方程为

Z(x,y,t)=-xδ

(5)

由当地流活塞理论，振动引起舵面任意位置处的扰动压力可以表示为

(6)

将式(5)带入式(6)，得

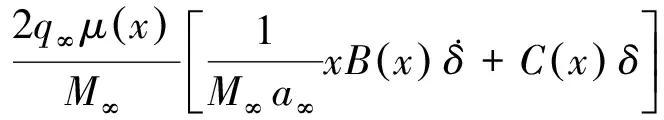
(7)

将式(7)确定的压力值对翼轴取矩并沿翼面积分，即可得到舵面非定常气动阻尼力矩，形式如下

(8)

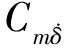
图3 典型三角舵随M∞和α的变化

2 舵结构系统的自激振动特性

2.1 舵结构系统飞行自激振动机理分析

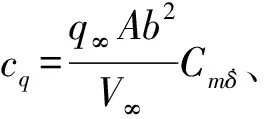
(3)区位交通条件。整体来看，区位指数与旅游经济联系网络具有显著负相关性，其他城市与郑州距离越远，区位指数越高，受郑州的旅游经济辐射就会变弱，这种“距离衰减”有增强的趋势。同时这也印证了在核心—边缘模型里的分析，边缘城市基本都距离郑州较远，并且处在行政边缘地区。而交通条件与旅游经济联系网络具有正相关，相关性系数维持在0.3左右，交通的通达性保障了旅游地的可进入性，对城市间的旅游经济联系具有积极促进作用。

c=c1+cq，k=kδ+kq

将式(8)带入式(1)并除去常值力项，得

fk(δ,e)=0

(9)

上式为自治系统振动方程，不需要外界激振，舵面相对舱体转动本身即能引起系统发生自激振动。忽略高次谐波项，文献[1]推导出系统自激振动角位移的振动频率ωe和振幅ρ控制方程为：

(10)

2πξJδρωeω0

(11)

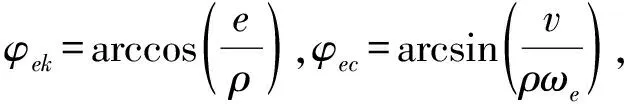
(12)

由式(10)～(12)可以看出：

(2) 间隙能够影响自激振动频率，使抖振频率低于舵结构系统固有频率，但它不是自激振动发生的主因，干摩擦及其曲线特征是舵结构系统产生自激振动的根源；

(3) 舵结构系统一经装配完成，干摩擦及其曲线特征以及结构粘性阻尼即得以确定，但气动附加阻尼会沿弹道发生变化，因此飞行当中舵结构系统是否能够发生自激振动、及其具体持续情况，还将取决于气动附加阻尼沿弹道的变化。

分析角加速度时不能忽略高次谐波项，问题更加复杂，但可以采用四阶Runge-Kutta-Fehlberg法直接对式(9)进行常微分方程数值积分，研究其高次谐波项的振动响应规律。

2.2 舵结构系统飞行自激振动现象及其模拟

舵结构系统的飞行自激振动现象已在多个飞行器的试验数据中观测到。以装有图3所示楔型剖面小展弦比后掠三角舵的某飞行器为例，试验测得弹体典型部位振动加速度时间历程和加速度功率谱曲线如图4和5所示。从中可以看出：在32～63 s时段飞行器出现严重抖振，且抖振加速度功率谱包含明显倍周期振动成分。试验数据分析表明：抖振时段不存在机械振源，且飞行动压尚小、气动噪声诱导的振动量级不会超出63 s以后量级水平，机械振源或气动噪声诱发抖振的可能性可以被排除。

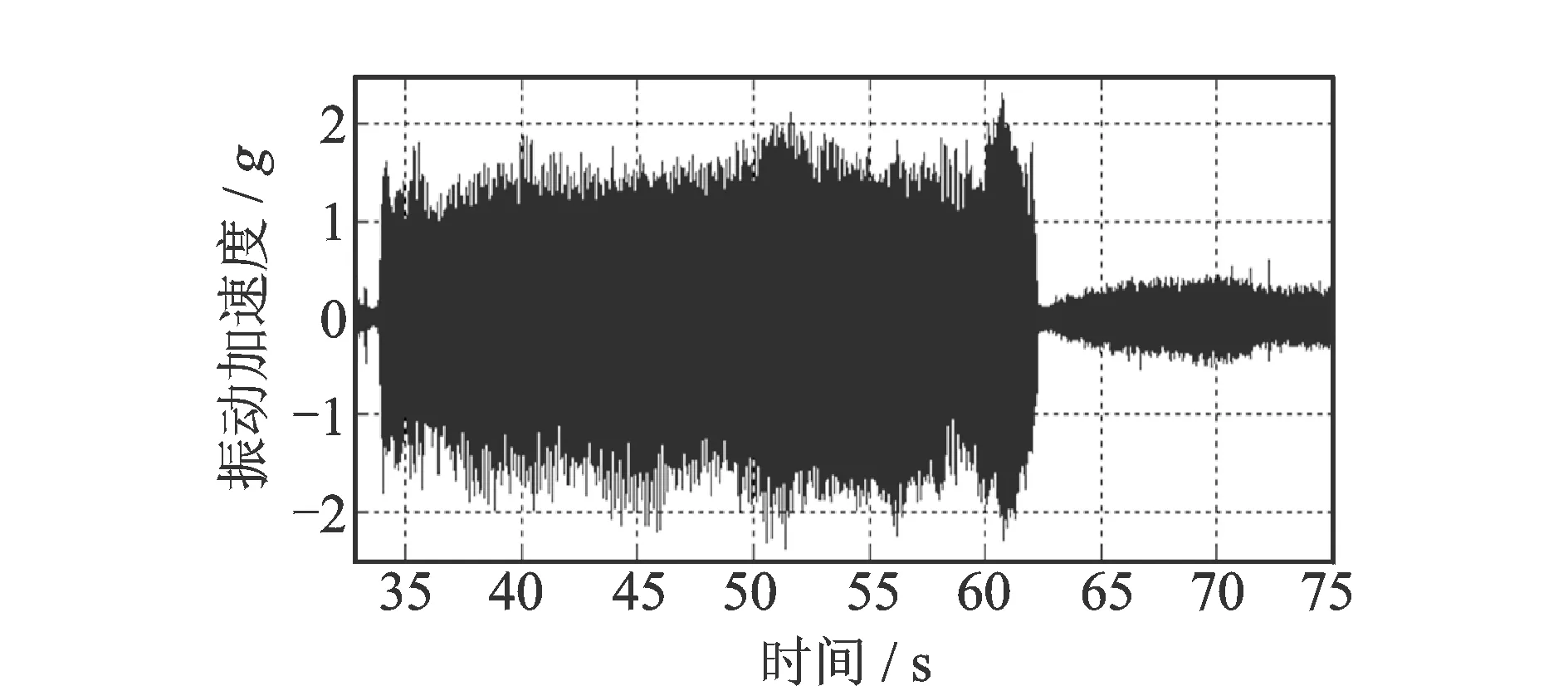
图4 典型部位振动加速度实测时间历程

图5 典型部位振动加速度响应谱实测结果

基于本文模型和方法，取舵结构系统典型设计和实测参数：固有频率ω0=100 Hz、阻尼比系数ξ=1.05%，干摩擦负载力矩Mf=2.5 N·m，k0=0.2，间隙量e=0.015°。由弹道数据和图3曲线可算得cq和kq，cq沿弹道的变化情况见图6，由于kq相对kδ是小量因而可以忽略不计。

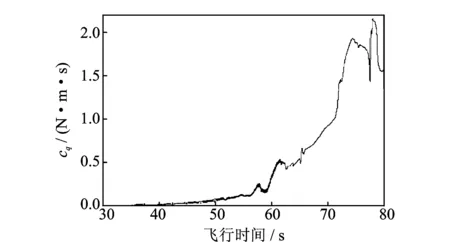
图6 cq沿弹道变化的时间历程曲线

给定v和vm，将cq，kq连同上述各项参数带入式(9)进行数值积分,首先验证2.1节理论方法的正确性，结果表明：任意给定vm，只要舵面转速小至满足式(12)关系式，舵结构系统即可发生自激抖振，数值模拟与理论方法给出的结论和规律一致。

依照舵面偏转情况，取典型偏转角速度v=16°/s，计算得到舵结构系统自激振动沿弹道的发生和持续情况见图7所示，振动加速度响应谱情况见图8所示。

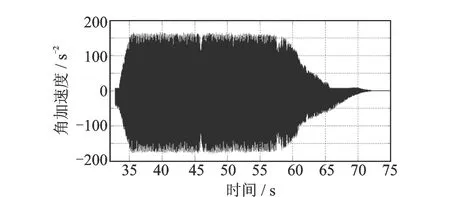
图7 自激振动时间历程计算模拟结果

图8 自激振动加速度响应谱计算模拟结果

对比自激振动现象的模拟和试验结果，情况表明：二者均在舵结构系统操纵起控时刻开始发生，随附加粘性阻尼提高、现象持续约30 s后自行消失；且自激振动加速度功率谱模拟结果包含与实测结果几近相同的倍周期振动成分。自激振动模拟计算结果与试验结果的现象和规律一致。

3 结 论

飞行器在低动压或稀薄大气中飞行时，常会经历一类特殊的自激振动现象，设计上需对其发生机理和规律进行了解和把握。本文针对工程应用需求，在含间隙和库伦摩擦舵结构系统非线性振动理论模型基础上，考虑舵面非定常气动阻尼力矩影响效应，提出舵结构系统飞行自激振动的分析方法。基于本文方法对舵结构系统自激振动的发生、持续和消失过程进行预示，能够得到与试验测量结果相一致的现象和规律，结果表明：

(1) 存在干摩擦及类似非线性环节时，只要粘性阻尼足够小，一定速度条件以下舵结构系统即可发生自激振动；

(2) 舵面非定常气动力矩能够发挥粘性阻尼的效果，随弹道变化当其升至一定水平时，即可拟制自激振动使其消失。

参考文献：

[1] 王成华,李国宏,李延松,等.含间隙和干摩擦舵结构系统的非线性动力学特征[J].振动与冲击，2013，32(19):22—27.WANG Chenghua,LI Guohong,LI Yansong, et al. Nonlinear dynamic characteristics for rudder structure system with dry friction and clearance[J]. Journal of Vibration and Shock， 2013, 32(19):22—27.

[2] 杨炳渊,宋伟力.应用当地流活塞理论的大攻角升力面颤振气动力表达式[J].上海力学，1999,20(3)：223—228.YANG Bing-yuan，SONG Wei-li. Expressions about aerodynamic forces of flutter for wing with high angle of attack by local flow piston theory[J]. Shanghai Journal of Mechanics, 1999, 20 (3):223—228.

[3] 陈劲松.超音速和高超音速机翼俯仰导数—当地流活塞理论解法[J].空气动力学学报，1991,9(4):469—476.CHENG Jingsong. Pitching derivatives of wing in supersonic and hypersonic stream—method for local flow piston theory[J]. ACTA Aerodynamica Sinica, 1991, 9(4):469—476.

[4] 闻邦椿.非线性振动工程应用[M].北京：机械工业出版社，2007.

[5] 白鸿柏.滞迟振动系统及其工程应用[M].北京：科学出版社，2002.

[6] 刘强，尔联洁，刘金琨.摩擦非线性环节的特性、建模与控制补偿综述[J].系统工程与电子技术，2002,24(11):45—52.LIU Qiang, ER Lianjie, LIU Jinkun. Overview of characteristics、modeling and compensation of nonlinear friction in servo systems[J]. Systems Engineering and Electronics, 2002,24(11):45—52.

[7] 杜仁慧，吴益飞，陈威，等.考虑LuGre摩擦的伺服系统自适应模糊控制[J].控制与决策，2013，28(8):1 253—1 256.DU Renhui, WU Yifei, CHEN Wei, et al. Adaptive fuzzy control for the servo system with LuGre friction[J]. Control and Decision, 2013, 28(8):1 253—1 256.

[8] 宋彦，高慧斌，田彦涛，等.伺服系统受摩擦扰动产生极限环的原因及稳定性分析[J].吉林大学学报(工学版)，2011，41(1):214—220.SONG Yan, GAO Huibin, TIAN Yantao, et al. Reasoning and stability of limit cycle generated by friction in servo system[J]. Journal of Jilin University (Engineering and Technology Edition), 2011，41(1):214—220.

[9] 王璇,张娟梅,周阳.含有Stribeck摩擦的高精度伺服系统相关分析辨识[J].光电工程,2010,37(12):143—146.WANG Xuan, ZHANG Juanmei, ZHOU Yang. Correlation analysis identification for high precision servo system with stribeck friction[J]. Opto-Electronic Engineering, 2010, 37(12)：143—146.

[10] Robert L Johnson. Investigation of wear and friction properties under sliding conditions of some materials suitable for cages of rolling-contact bearings[R]. NASA19930092108.

[11] Oden J T，Tworzydlo W W. Progress in the theory and modeling of friction and in the control of dynamical systems with frictional forces[R]. AD-A208763.

[12] 马晨波，朱华，陆斌斌.引入特征粗糙度参数的Stribeck曲线试验研究[J].摩擦学学报,2010,30(5):466—471.MA Chenbo, ZHU Hua, LU Binbin. Experimental study on stribeck curves based on characteristic roughness[J]. Tribology，2010, 30(5)：466—471.