住房养老反向抵押贷款的美式期权特征与蒙特卡罗模拟定价

马俊海

浙江大学 城市学院，浙江 杭州 310015

一、引 言

随着老龄化现象日趋严重，住房抵押贷款作为“以房养老”的创新型金融产品逐渐得到更多关注;近些年来，有赎回权反向抵押贷款由于其可提前赎回特点，开始得以迅速发展与广泛应用。因此，对其进行科学合理定价具有重要现实意义。目前，反向抵押贷款的定价方法主要有绝对定价法和相对定价法两种类型;绝对定价法是指根据反向抵押贷款现金流的特征，运用现金流净现值法则加以分析，主要适合于无赎回权反向抵押贷款定价。而相对定价方法主要利用标的价格与衍生产品价格之间的关系，运用期权定价理论加以分析;由于有赎回权反向抵押贷款具有很强的期权特征，因此从隐含期权角度，基于期权定价理论对其进行科学定价也具有重要学术价值。国外关于反向抵押贷款定价问题研究开始于20世纪90年代。Y．K．Tse(1998)［1］以新加坡无赎回权反向抵押贷款为研究对象，分别研究了固定利率以及浮动利率下的定价模型。Caplin，Andrew(2002)［2］解释了抵押贷款产品定价决定因素，并给出了无赎回权反向抵押贷款定价的理论模型。Sinai，Todd and Nicholas Souleles(2005)［3］提出了一个新的反向抵押贷款定价的公式，指出有赎回权反向抵押贷款会更吸引投资者。Brigo，D．and Mercurio，F(2006)［4］运用LSM方法分别对单标的和双标的美式期权进行定价研究，并指出拟蒙特卡罗模拟方法在定价双标的美式期权上的不足之处。

国内关于反向抵押贷款研究集中于反向抵押贷款的保险精算定价方法上。石卉和刘晓玲(2008)［5］研究了有赎回权的住房反向抵押贷款的欧式期权定价方法，并进行了实证分析;李瑾卓(2009)［6］对有赎回权反向抵押贷款的定价模型进行研究，并将结果与无赎回权反向抵押贷款定价模型下的结果进行比较。

综上，近几年对有赎回权反向抵押贷款定价问题主要基于欧式期权定价视角加以分析。本文主要基于美式期权定价视角，研究反向抵押贷款的期权定价模型，并运用蒙特卡罗模拟方法加以数值模拟计算。

二、有赎回权反向贷款期权定价的理论分析框架

与无赎回权反向贷款相比，有赎回权反向抵押贷款蕴含着很强期权特征，因此其价值主要是取决于两个关键因素，即:无赎回权反向抵押贷款的价值与隐含期权价值，其价值等于二者之和。关于无赎回权的反向抵押贷款定价问题，常用模型是由路静等(2009)［7］分析的保险精算模型，该模型无疑是无赎回权反向抵押贷款定价的经典模型;但是，由于其假设限定非常多，使得定价精度大大减弱。本文将在保险精算模型的基础上进行修正，以使其更符合实际。对于隐含期权价值的研究，目前大多采用欧式期权的定价方法;而实际上，这种理解是不符合实际的，在反向抵押贷款实际业务中，允许借款人在市场环境发生变化时选择提前偿还贷款并且将住房资产的抵押权赎回。因此，美式期权定价方法更适合用来解决有赎回权反向抵押贷款的定价。为此，本文选用双标的最小二乘蒙特卡罗模拟(LSM)方法加以分析。

(一)无赎回权反向抵押贷款的改进定价模型

根据阮龙江(2012)［8］的研究，无赎回权住房反向抵押贷款的价格主要取决于三个因素:还款利率、住房价值的波动以及借款人的寿命。本文主要针对路静等(2009)分析的保险精算模型，选择前两个因素进行修正，并将修正后的因素模型应用到住房反向抵押贷款定价模型中，即可得到修正的无赎回权反向抵押贷款定价模型。基于以上分析，本文对无赎回权反向抵押贷款一次性支付方式下的定价模型进行改进，并对模型做如下假设:1)借款人只有一个，并且用来申请反向抵押贷款的房屋没用于其他的抵押贷款;2)借款人的死亡时间均为每年年初;3)抵押房屋在借款人死亡后立即进行处置，二者之间不存在时间差;4)住房反向抵押贷款所涉及的各种手续费设定为房价的一个固定比例。

一次性支付方式下修正无赎回权的住房反向抵押贷款定价模型可表示为:

其中相关变量参数意义表述如下:

Ht—住房反向抵押贷款合同在第t年时房屋的价值;

rt—住房反向抵押贷款第t年包含贷款机构正常利润的年利率;

T—借款人的平均剩余寿命。

终生年金支付方式下修正无赎回权反向抵押贷款的定价模型如下:

从上述修正后定价模型可以看出，申请人可领取的贷款数额主要取决于还款利率、住房资产每期的价值和申请人的死亡率。

(二)有赎回权反向抵押贷款的隐含期权价值特征

反向抵押贷款最主要特征就是隐含期权特征，即反向抵押贷款可以提前偿还。因此，可以看作是一个具有隐含期权产品。在有赎回权住房反向抵押贷款业务中，借款人拥有一种潜在选择权，即在住房资产价值上升时，按照执行价格购买住房资产产权的权利;这种潜在选择权即为隐含看涨期权。此时，标的资产为住房资产，执行价格为贷款的本息额，执行时点为合同有效期内的任意时点。

1．一次性支付方式下的期权价值特征。在一次性支付方式下，借款人可以一次性得到一笔贷款，贷款终值可以看作是看涨期权的执行价格;就贷款机构而言，这个执行价格由借款人抵押的住房资产现值扣除期初各种相关费用得出。因此，在随后的合同期间内，一旦借款人发现自有住房资产的价值上升，借款人就会执行该看涨期权。假设一次性支付方式下，借款人在贷款期初可以一次性得到一笔贷款数额为λH0的贷款;如果在t时刻，房屋价值上升或者还款利率降低，则贷款人会选择提前偿还贷款。具体来说，当条件有利时，借款人在t时刻就会选择提前偿还已发生的贷款本息和，即然后，以t时刻房价Ht重新购进一份住房反向抵押贷款合同，一次性得到的贷款数额变为λHt。

2．终生年金支付方式下的期权价值特征。在年金支付方式下，借款人每年得到固定数额贷款，固定数额贷款现值为住房资产的现值减去期初的各种相关费用。对于借款人来说，实际上是将自有产权的住房，在不确定的金融市场中，分期分批出售给贷款机构，而贷款机构则通过分期分批给付贷款的形式，将抵押房产的产权逐渐收购进来。由于金融市场的不确定性，住房资产的价值会发生上下波动，当某期住房资产的价值上升并且超过该期给付的贷款数额时，借款人就会执行该看涨期权，用当期的贷款数额赎回当期住房资产所占比例的产权。因此，在这种支付方式下，如果借款人在终止住房反向抵押贷款业务后，又以新的价格重新购进一份住房反向抵押贷款合同，那么有赎回权住房反向抵押贷款合同就可以看作是一系列看涨期权的组合。

终生年金支付方式下，借款人是否提前偿还贷款主要取决于每年支付的年金数额是否增加。因此，本文对住房反向抵押贷款提前偿付模型作如下假设:1)假设住房反向抵押贷款合同的期限是T年(T取决于借款人的寿命)，在每一年初支付年金，数量设为D;2)假设反向抵押贷款还款利率为1年期国债收益率+差额利率;其中，每年差额利率保持不变，设定为m;进一步假设，第t年即期利率为rt;3)由住房反向抵押贷款的特点可知，当借款人决定提前偿还时，必须用其抵押住房进行偿还。此处，假设抵押住房在贷款期初的价值为H0，在贷款期末的价值为Ht;4)为了简化模型，假设借款人在签订贷款合同前已经支付了各项费用。

根据以上假设，判断借款人在第t年会不会提前偿还贷款，基本依据是:首先，计算出抵押住房期末价值扣除已经获得贷款本息和以后所剩资金数量，再根据第t年即期利率计算得出未来可获得年金数额;如果该数额大于当前借款人每年可获得的年金数额，借款人就会选择提前结束贷款;否则，就会持有住房抵押贷款合同直至到期。也就是说，如果满足条件，借款人应该提前偿还贷款。此时，借款人可在市场上按新的条件购进一份新的住房反向抵押贷款合同，那么借款人在每一期可获得的收益(或借款人可节约的成本)即为:(Ht－Lt)

三、标的变量随机动态模型的选择确定与参数估计

由上分析，住房反向抵押贷款定价过程中关键因素是利率及房价波动;无论是无赎回权还是有赎回权住房反向抵押贷款，利率与房价决定了借款人可以得到的贷款数额以及借款人是否会提前偿还贷款，并进而影响到贷款机构的收益以及开办住房反向抵押贷款业务的积极性，因而有必要对利率以及住房资产的价值进行预测，以对住房反向抵押贷款正确定价。

(一)利率动态过程的选择确定

通过对住房反向抵押贷款价值构成的分析，首先要对住房反向抵押贷款的还款利率进行模拟。由于本文研究的产品均假设期权执行发生在每年年初，因此决定选用一年期国债利率作为还款利率。关于利率动态模型确定，常用的是单因子模型，典型单因子模型主要有Merton模型、Vasicek模型以及CIR模型;Chan(1992)提出了更一般的CKLS模型，具体形式为:

其中，通过ρ的改变可以得到以上所涉及的三种模型，当然也可以得到很多其他模型。为此，本文拟采用CKLS模型作为利率动态过程的连续扩散部分。进一步分析，由于央行货币政策突然变化、宏观经济波动以及其他突发事件影响，利率市场通常呈现出一种跳跃行为，而上述单因子利率模型并没有考虑到利率市场上某些时刻的利率异常变动情况;因此，本文拟在上述单因子模型基础上引入跳跃成分，以便更好模拟利率动态变化。目前，利率模型中的跳跃类型主要有泊松分布、均匀分布、正态分布等;泊松分布没有考虑到跳跃的幅度;均匀分布虽然考虑了利率跳跃幅度，但是假设利率每次跳跃的幅度都一样。因此，本文主要选取正态分布来描述跳跃幅度变动。

基于以上分析，本文将CKLS单因子模型和正态分布跳跃因子有机结合，建立CKLS—JUMP利率动态模型。该模型不仅可以很好地描述利率模型的连续扩散部分，同时还能体现由于政策因素等造成的市场利率的较大偏离，模型具体形式如下:

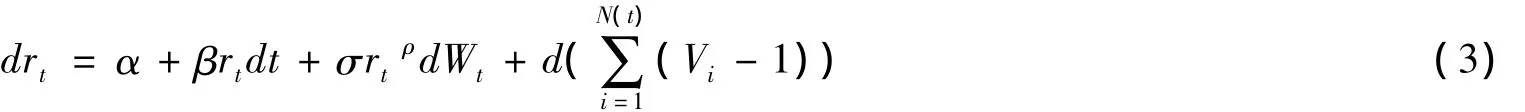
其中，α、β和σ均为常数，Wt表示标准布朗运动，N(t)表示强度为λ的泊松过程;Vi表示一系列非负并且同分布的随机变量且Yi=log(Vi)服从正态分布。

(二)房价动态过程的确定

对房屋未来价值评估的方法主要有两种:一是建立随机动态模型，这是目前房产价值研究主要采用的模型;在随机动态模型中，住房价值变动被视为“几何布朗运动”。二是通过分析影响房地产价格的因素，建立多元统计模型进行回归预测;但是，房地产价格的多元线性回归模型由于影响因素较多，很难对这些因素的未来走势做出正确估测，因此会大大影响房产价格预测的准确性。本文决定采用随机动态模型作为评估住房资产价值的主要模型。进一步分析，一般随机动态模型并不能很好地描述房地产价格的变化，因为房地产市场有其自身的特点，比如房地产泡沫等，同时国家关于房地产的政策也会对房产价格产生较大影响。政策因素的变动并不是经常性的，而是偶然性的，突然性的，这样的变动往往引起房产价值的突然变动，可以将这种现象理解为“跳跃”。因此本文决定在随机扩散模型基础上加入跳跃因素作为预测房产期末价值模型，具体的房产价值预测模型如下:

(三)标的变量随机动态模型的参数估计

常见的利率期限结构参数估计方法大致有五类:广义矩估计(GMM)方法、极大似然估计(MLE)方法、卡尔曼滤波(Kalman Filter)、马尔科夫链蒙特卡罗估计(MCMC)方法以及非参数估计方法。由于资产动态模型所涉及的参数数量比较多，前面几类方法都不能得到有效运用，因此本文采用目前比较成熟的参数估计方法—MCMC方法。MCMC方法的主要优点是不需要添加平稳性假设，同时有限样本推断成为可能，通过潜在变量的蒙特卡罗积分得到参数的联合后验分布。近年来，MCMC方法逐渐应用到金融资产定价模型的参数估计上来，由于该方法将马尔科夫过程引入到蒙特卡罗模拟中，使得得出的后验分布更加稳定，因此保证了模型的稳定性，最终得出的模型参数也更精确。

1．利率动态过程的MCMC参数估计。对本文选择的CKLS利率模型进行欧拉离散化，得到:

当Δt=1时，离散式变为:

其中，εt和Pt分别代表标准正态分布变量和伯努利分布变量。由平稳性定义可知:

由于跳跃幅度Yt服从正态分布，利率变化就可以用正态密度近似。由式(5)可得:

参数 θ=(α，β，λ，ρ，σ，μn，σn)基于数据观测值集合的对数似然函数为:

根据贝叶斯原理，参数向量θ基于数据r集合的条件分布可以通过后验密度p(θ│r)得到，即:

其中，p(θ│r)是似然函数，π(θ)是参数θ的先验分布。得到先验分布后，根据历史数据，就可以估计出参数变量的后验分布。针对前述CKLS－JUMP模型，具体的吉布斯抽样步骤如下所示:

(1)对l和θ进行初始化;

(2)随机抽样:

从 lt│l/t，r，θt=1，2，3，．．．，n中抽取lt，从α│r，l，β，ρ，μ ，σ ，σn，λ中抽取α;

从β│r，l，α，ρ，μ，σ，σn，λ中抽取β，从ρ│r，l，α，β，μ，σ，σn，λ中抽取ρ;

从μ│r，l，α，β，ρ，σ，σn，λ中抽取μ，从σ│r，l，α，β，ρ，μ，σn，λ中抽取σ;

从σn│r，l，α，β，ρ，μ，σ ，λ中抽取σn，从λ│r，l，α，β，ρ，μ，σ ，σn，中抽取λ;

(3)重复以上步骤。

将步骤2)产生的抽样结果作为下一轮抽样初始值，重复步骤2);再将新一轮抽样结果作为下一次抽样的初始值。不断进行上述步骤，当经过足够的燃烧期后，吉布斯序列就能收敛到一个与初始值无关的平稳分布，即后验分布。同时由于燃烧期内产生的参数值是不平稳的，舍弃燃烧期内的样本后即可得到平稳的分布，进而完成参数估计过程。

2．房价动态过程的参数估计。对前面建立的利率模型进行欧拉离散，当Δt=1时，离散式变为:

其中，εt和Pt分别代表标准正态分布变量和伯努利分布变量，由平稳点定义有:

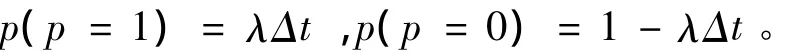
由于跳跃幅度Yt服从正态分布，利率变化就可以用正态密度近似。由式6)可得:

参数θ=(β，λ，σ，μn，σn)基于数据观测值集合的对数似然函数为:

根据贝叶斯原理，参数向量θ基于数据r集合的条件分布可以通过后验密度p(θ│r)得到，即:

其中p(r│θ)是似然函数，π(θ)是参数θ的先验分布。得到先验分布后，根据历史数据，就可以估计出参数变量的后验分布。针对前述CKLS－JUMP模型，具体的吉布斯抽样步骤如下所示:

(1)对参数l和θ进行初始化;

(2)随机抽样。

从 lt|lλ，H ，θt=1，2，3，…，n中抽取 lt，从 β|H ，l，μ ，σ ，σnλ 中抽取 β;从μ |H，l，β，σ，σn，λ 中抽取 μ ，从 σ |H，l，β，μ，σn，λ 中抽取 σ ;

从 σn|H，l，β，μ，σ，λ 中抽取 σn，从 λ |H，l，β，σ，σn，μ 中抽取 λ ;

(3)循环重复与利率动态步骤3类同。

四、反向贷款隐含期权定价的双标的LMS方法

(一)双标的LSM方法的基本原理

由于赎回权反向抵押贷款具有多标的美式期权特征，因此蒙特卡罗模拟将成为解决其定价问题的重要手段。本文针对利率及房价两个标的变量，拟用双标的变量最小二乘蒙特卡罗方法进行银行资产负债隐含期权定价研究。根据期权理论，假设借款人签订的住房反向抵押贷款合同的期限为T，即隐含期权的到期日为T，借款人选择提前偿还贷款的时间为t，即执行时间为t。由于该隐含期权在T时刻收益不仅仅受时刻T的利率和房价影响，还可能受到从贷款存续期间利率及房价运动路径影响，因此该隐含期权在执行时间t价值为:

其中，EQ为风险中性概率测度下的期望算子，r为合适的贴现利率，f(Rt，Ht)为从贷款开始日至到期日之间隐含期权标的变量变化路径，由利率和房价共同决定。双标的LSM方法就是通过随机抽样模拟计算式(7)，得到期权价值的一种数值分析方法。基本实现步骤为:1)生成单一标的资产价格的样本路径;2)从期权到期日开始逆向求解，得到每条样本路径上的最优期权执行时间和相应的期权收益;3)将每条样本路径上的期权收益用无风险利率贴现，然后取其均值即可得到标的期权模拟价值。

(二)隐含期权定价的双标的LSM方法的基本过程

1．样本路径生成。通过随机抽样生成利率的样本路径R0，．．．Rt，;;;RT及房价的样本路径H0，．．．Ht，;;;HT。为了应用最小二乘蒙特卡罗方法，需要将式(3)及式(4)离散化:

如果Δt足够小，可以忽略多次跳跃，利率模型和房价模型可以近似为:

当Δt=1时，离散式变为

由式(8)及式(9)，就可以得出最小蒙特卡罗模拟的一条样本资产运动轨迹迭代式:hj(X0，．．．Xt，．．．XT)，j=1，2，;;;M 。其中，M 为模拟的样本路径数量。M 次模拟后得到样本路径矩阵PM×(N+1)。

2．计算每条样本路径的最优执行时间和隐含期权收益。在任意时刻i，反向抵押贷款隐含期权作为看涨期权，在样本路径上的内在价值为:

由于反向抵押贷款隐含期权可以提前偿还，因此最优执行时间的选择，主要通过对立即执行期权的即时收益与继续持有期权的期望收益之间大小比较来进行，即:

EQ为在当前样本值条件下继续持有期权的期望收益，依赖于下一步执行期权决策，因此主要通过逆向求解方法得出。LSM方法主要通过近似模拟期望收益来实现对式(11)的模拟。本文中LSM方法通过回归得到当前样本值的一个简单三次多项式来对式(11)中的条件期望进行近似逼近计算，即:

把所有样本路径在时刻i的价格Xi作为X值，将相应的样本路径上未来收益作为 Y 值，运用线性回归，求得回归系数 a1，a2，a3，a4。

为了计算每条样本路径上最优执行时间和相应期权收益，从贷款到期日开始计算。在到期日N时刻，执行期权，收益为max(－K，0)。在时刻N－1，如果该隐含期权在样本路径上是溢价的，即＞K，则考虑执行期权，但是否真执行期权还要分析继续持有期权至到期日的期望收益:如果它小于＜K，则立即执行期权，即在此刻偿还贷款;否则，继续持有期权，运用式(11)近似计算继续持有期权的期望价值。

根据提前执行期权的溢价性前提条件，在此只以在N－1时刻处于溢价的样本路径为基进行回归。为此，选用以下回归方程近似继续持有期权的期望收益:

以此类推，便可得到时刻N－2，N－3，．．．，0，继续持有该隐含期权的期望收益。对于每条样本路径j，期权在唯一时刻t∈{0，1，．．．N}执行。因此，样本轨迹在t时刻继续持有期权的期望收益为:

其中，Ji是时刻i期权处于溢价(即＞K)的样本路径集合。在初始状态，令tj=N，在时刻N－1，如果继续持有期权，则tj不变;如果执行期权，则tj=N－1，依此类推。由于每条利率样本路径只有一个最优执行时间，因此只保存最新的tj，最后便求得每条样本路径的最优执行时间。相应地，样本路径j在最优执行时间tj的期权收益为

3．计算每条样本路径期权收益贴现的平均值。经过M次模拟后得到M条利率样本路径以及每条样本路径上最优执行时间的期权收益:

由于每条样本路径执行时间不同，对期权收益贴现因子e－rtjk也不同，必须按每条路径相应贴现因子贴现，然后求均值期望收益的估计值，即贷款隐含期权LSM模拟的一个模拟值:

五、实证模拟

(一)标的变量动态过程

1．利率动态模拟结果。本文针对住房反向抵押贷款合同特征，选用美国1年期国债利率作为住房抵押贷款利率标的变量;首先，选取原始序列中2008年之前的数据并对这些数据进行平稳性检验，在Eviews软件中实现的结果如下表1所示:

表1 利率数据序列的平稳性检验

从表中可以看出，统计量t值大于三种显著性水平下的临界值，说明原始数据是平稳的，可以用于回归分析。从2008年末开始，一年期国债利率的数据急剧下降，这也是本文在利率模型中加入跳跃原因。利率模型参数估计结果如表1:

表1 利率模拟结果

由此得出，经过模拟后所得到的美国一年期定期国债利率迭代式为:

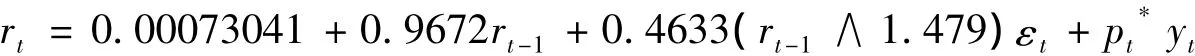
(2)住房价格指数动态模型。本文选用美国住房价格销售指数(HPI)作为估计房价模型参数的数据，反映美国住房价格变化趋势的指数。在运用Winbugs软件对HPI动态模型进行参数估计时，选用股票价格指数先验分布，这是因为房屋价格波动与股票价格波动存在一定联动，在一定程度上可以反映指数的共有特征。房屋价格动态过程模拟结果如表2:

表2 房价模拟结果

经过模拟后的房价模型迭代式为:

(二)无赎回权反向抵押贷款定价

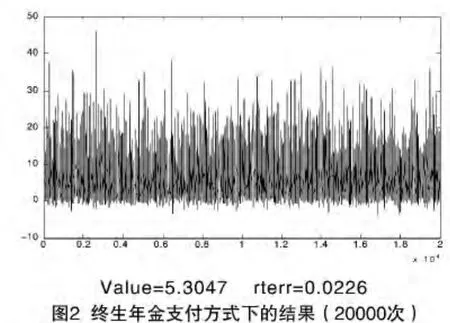
本文选用一美国案例，假设一位年龄为65岁老人，拥有住房资产价值100美元，在2011年4月1日跟银行签订了一份住房反向抵押贷款合约。由前分析，年龄为65老年人的平均寿命为80岁，因此这份住房反向抵押贷款合同的期限可以设定为15年。当前美国一年期国债利率为0．19%，差额利率m设为3%。下面分别讨论终生年金支付方式下的住房反向抵押贷款隐含期权的价格。运用修正无赎回权反向抵押贷款模型来模拟无赎回权反向抵押贷款价格。经由Matlab程序运行模拟住房反向抵押贷款价格实证结果。其中，利率初始值R0=0．19%，差额利率m=3%，到期日T=15，贴现利率采用R0，每个时间间隔为一年，即每年都有执行提前偿还权利，模拟样本路径数分别为M=15000和M=20000。具体模拟结果见图1、图2。

(三)隐含期权价格实证模拟

1．模拟结果。本文为了最终计算有赎回权反向抵押贷款价格，采用与无赎回权反向抵押贷款相同条件的产品。假设一位年龄为65岁老人，拥有住房资产价值100美元，在2011年4月1日跟银行签订了一份住房反向抵押贷款合约。由前面分析，年龄为65老人的平均寿命为80岁，因此这份住房反向抵押贷款合同的期限可以设定为15年。当前美国一年期的国债利率为0．19%，差额利率m设为3%。下面主要讨论终生支付方式下的住房反向抵押贷款隐含期权的价格。基于LSM方法模拟住房反向抵押贷款的提前偿还行为，并对以利率和房产价值为双标的资产的隐含美式看涨期权定价。经由Matlab程序运行的模拟贷款隐含期权定价的实证结果。其中，利率初始值R0=0．0319，期权执行价格分别为一次性支付方式和终生年金支付方式下住房反向抵押贷款的价格，这里分别取:K1=77．5，K2=5．45，到期日T=15，贴现利率采用R0，每个时间间隔为一年，即每年都有提前偿还的权利，模拟样本路径数分别为M=150000和M=200000。具体的模拟结果见图3、图4。

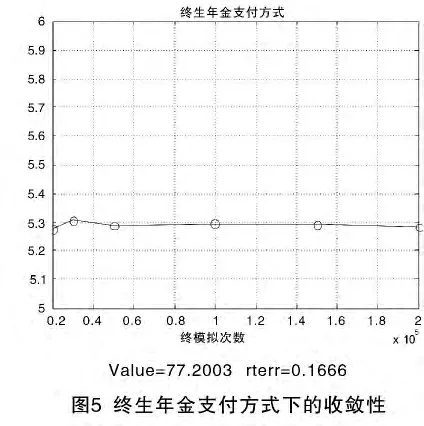
2．收敛性与计算效率分析。本文通过逐渐增加样本路径数目M，以得到收敛期权值的稳定性来判断收敛性。当样本路径分别为15000，20000，30000，50000，100000，15000，200000 时，所得期权值分别为 1．2886，1．4049，1．2989，1．3171，1．3077，1．2960。由图5可以看出随着模拟次数的增多，期权值在1．30上下小幅波动，表明收敛性良好。本文模拟算法直接使用MATLAB提供的标准正态随机数生成函数randn，确保了随机数的独立性和均匀性。实验表明，在P41．4GHz CPU的计算机上，N=60，M=10000的运行时间不超过10分钟。因此无论从收敛性还是计算时间上看，反向抵押贷款隐含期权计算结果良好。

3．定价结果说明。住房反向抵押贷款在美国市场于1980s才开始兴起，最初由于传统养老观念以及政府政策的原因，发展并不是很好，直到20世纪末美国的住房反向抵押贷款才开始得到发展。发展之初，大多数反向抵押贷款是以无赎回权的形式存在的，直到最近几年，有赎回权的住房反向抵押贷款才开始受到关注。因此关于住房反向抵押贷款的定价研究是比较少的，尤其是住房反向抵押贷款中隐含期权价值的确定更少，所以对各种方法得到的不同的隐含期权值，难以判定结果是否合理。从本文所得结果的收敛性可以看出，无论是无赎回权反向抵押贷款的定价，还是有赎回权的住房反向抵押贷款隐含期权的定价，都呈现出一定的收敛性，因此定价结果是比较可信的。同时，从数值大小来看，隐含期权的价值大约为1．30，与每期得到的贷款数额5．45相比，大约是每期贷款数额的23．85%，这与银行存贷款隐含期权的20%相比，也是非常接近的，因此本文对有赎回权反向抵押贷款隐含期权的定价是比较合理的。

六、结论

本文主要基于美式期权定价视角，分析了反向抵押贷款的期权定价模型，并运用蒙特卡罗模拟方法加以数值模拟计算。研究的主要结论有:(1)基于美国一年期国债收益率及全国住房价格销售指数实际变动情况，选取跳跃扩散来模拟利率与房价的变动，改变了传统模型中将利率设为固定的国债收益率及将房价的增长率设为固定值的缺陷。(2)无赎回权反向抵押贷款由于其本身的特点，适合用保险精算方法进行定价，经过对利率及房价以及借款人剩余寿命的动态模拟后，使得这些因素更加符合市场变量及老年人自身的实际状况，从而使得定价结果比简单的设定固定增值率时的结果更加精确。(3)有赎回权反向抵押贷款由于具有可提前赎回住房资产的权利，因此适合用期权方法来定价。本文运用美式期权定价方法对有赎回权反向抵押贷款隐含期权进行定价，并最终得到有赎回权反向抵押贷款的价格。

［1］Y．K．Tse．Modelling Reverse Mortgages，1998．Asia Pacific Journal of Management，Vol．12，No．2:79 －95．

［2］Caplin，Andrew，2002．Turning Assets into Cash:Problems and Prospects in the Reverse Mortgage Industry．in Olivia S．Philadelphia:University of Pennsylva－nia Press．

［3］Sinai，Todd and Nicholas Souleles，2005．Owner Occupied Housing as a Hedge Against Rent Risk．Quarterly Journal of Economics，Vol，120，No 2:63 －89．

［4］Brigo，D．and Mercurio，F，2006．Interest Rate Models Theory and Practice，with Smile，Ination and Credit，Heid－elberg:Springer－Verslag ．

［5］刘晓玲．中国反向抵押贷款产品创新研究［D］．北京:首都经贸大学工商管理学院，2008．

［6］李瑾卓．有赎回权的住房反向抵押贷款定价模型的定量研究［J］．韶关学院学报，2009(12)．

［7］路静，高鹏，董纪昌．基于保险精算的住房反向抵押贷款定价研究［J］．管理评论，2014(4)．

［8］阮龙江．基于隐含期权的固定利率住房抵押贷款定价研究［D］．广东商学院，2012．