采用Karatsuba 算法在FPGA 上实现双精度浮点乘法

康 磊，徐英卓

(西安石油大学计算机学院，陕西西安710065)

浮点运算广泛应用于诸多领域，特别是在科学计算、数值分析和信号处理等方面，如数字滤波器、FFT、图像处理等。在所有的浮点算术运算中，乘法是其核心算法之一，如何构建高效的浮点乘法器一直是人们关注的焦点。随着FPGA技术的发展，由于FPGA器件本身的优势——速度、逻辑资源、丰富的IP核等，使得采用FAPG实现通用高性能的运算器成为可能。按照IEEE754中定义的双精度浮点数的尾数有53 bit，采用FGAP实现53 bit×53 bit的硬件乘法器需要占用大量的硬件资源［1-2］。本文详细说明了采用Karatsuba算法在FPGA上实现了双精度浮点乘法器的过程。

1 双精度浮点数格式

IEEE754是使用最广泛的浮点数运算标准，常用的浮点数有单精确度(32 bit)和双精确度(64 bit)2 种［3］。

单精度浮点数的格式:

双精度浮点数的格式:

浮点运算器的运算包含加、减、乘、除、平方和开方等。通常情况下，在运算之前需要将浮点数分解为符号位、阶码和尾数，然后进行运算，各部分运算结束后，还要经过舍入和规格化，最后再将符号、阶码和指数重构得到结果。本文只讨论双精度浮点数的乘法运算。浮点乘法器虽然是一个简单的算术单元，但由于它需要一个53 bit位的乘法器，因此在使用FPGA实现时需要考虑硬件资源的消耗和时间。

2 浮点乘法运算过程

浮点乘法运算规则的通式为:X×Y=(－1)SX+SY×(MX×MY)×2EX+EY。式中X和Y为2个输入的浮点数，其中SX和SY是符号位，MX和MY是尾数，EX和EY是阶码。双精度浮点乘法运算流程如图1所示，其操作步骤如下:

(1)输入的操作数先是被分成1 bit符号位、11 bit阶码和53 bit尾数(包括隐藏位);

(2)判断2个操作数中是否存在0，若是则转向(9);

(3)2个运算数的符号位进行异或运算，结果就是乘法运算结果的符号位结果;

(4)将阶码相加，然后减去1 023，得到乘法运算的阶码结果;

(5)尾数相乘，得到106位的结果;

(6)对运算的结果进行规格化处理，即对尾数的106位结果左移至最高位是1为止，然后取第106位到54位;

(7)对尾数的53到1位按照舍入原则进行舍入操作，通常采用的默认模式是最近舍入(Round to Nearest);

(8)对阶码结果进行判溢处理，设置阶码和尾数的最后结果;

(9)将符号位、阶码和尾数的结果重新拼接成64 bit的运算结果。

图1 浮点乘法运算流程Fig．1 Flowchart for floating-point multiplication

3 用Karatsuba算法实现尾数乘法运算

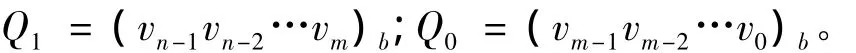
因此有

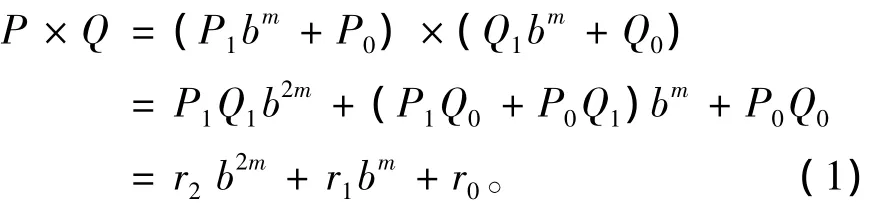
其中:r2=P1Q1;r1=P1Q0+P0Q1;r0=P0Q0。

从式(1)可以看出，实现P×Q可以将乘法器的位数由n位降低为m位(m=n/2)，乘法器的尾数降低了一半，但是需要做4次乘法操作。

Karatsuba乘法算法［4］是将式(1)中的r1做如下变换:

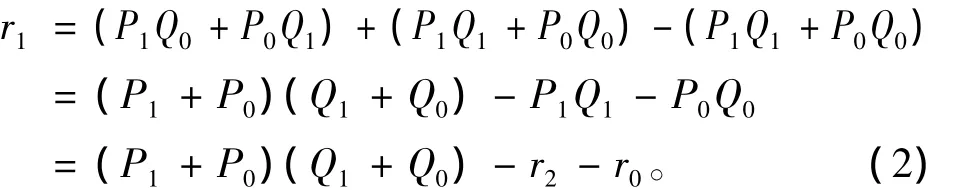
变换后的式(2)中r1的2次乘法运算变成了1次，但需要增加加法的次数，而加法的运算时间要比乘法小得多。

Karatsuba算法还可以进一步扩展，将2个乘数分解成更多的项数。若将2个乘数表示分解为3项，P和Q可写为

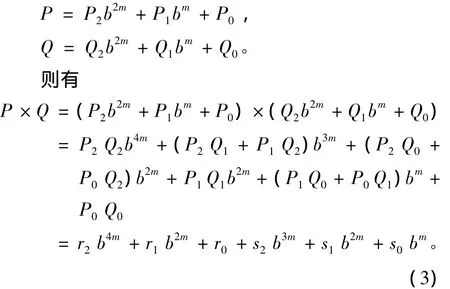
其中:r2=P2Q2;r1=P1Q1;r0=P0Q0;s2=P2Q1+P1Q2;s1=P2Q0+P0Q2;s0=P1Q0+P0Q1。

式(3)使得乘法器的位数更少，但是需要9次乘法运算，若采用式(2)的方法对式(3)中的s2～s0进行如下变换:可以将乘法运算减少为6次。

4 FPGA实现

本文采用Altera公司的EP2C70896C6芯片实现浮点乘法器，由于该芯片内部乘法器单元是18 bit×18 bit的。因此，将双精度浮点数的53 bit(含隐含的整数位1 bit)尾数进行如下分解(即式(3)中m=18，b=2):

从式(3)和式(4)可以看出，实现r0～r2需要18 bit的无符号乘法器，s0～s2需要19 bit的无符号乘法器。由于EP2C70896C6芯片内部的乘法器是18 bit的，因此，实现19 bit的乘法需要2个18 bit的乘法器，为了节省资源需要对其运算过程再次进行改进。19 bit乘法器的改进算法如图2所示。

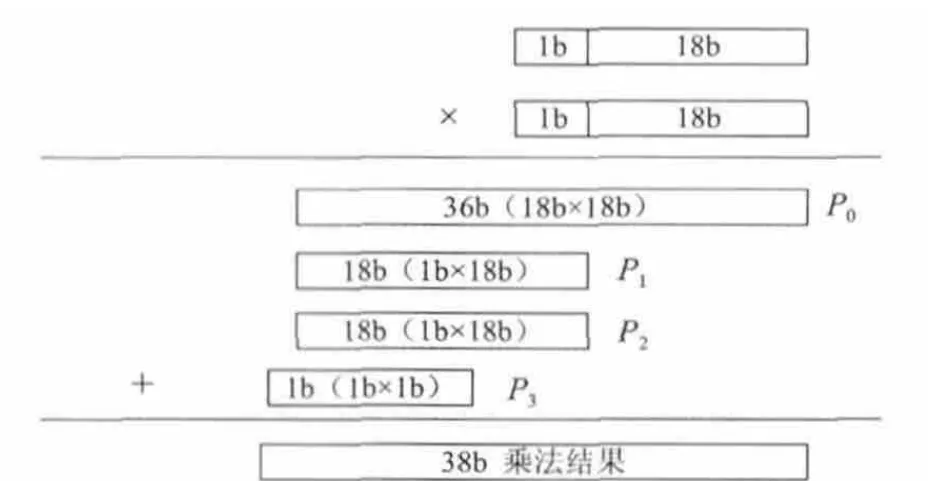
图2 19 bit乘法器改进算法Fig．2 Improved algorithm of 19bit multiplier

图2 所示计算过程中的中间结果P0可以使用1个dsp_18(18 bit×18 bit的乘法单元)来实现，而P1～P3可以只用逻辑资源来实现。这样计算53 bit的尾数乘法只需要6个dsp_18就可以实现了，而且也可以有效减少电路时延。

图2方法实现的19 bit×19 bit的Verilog HDL模块如下:

module mul_19b(a，b，out);

input［18:0］a，b;

output［37:0］out;

wire［37:0］out_P0，out_P1，out_P2，out_P3;

wire［35:0］out_Pt0;

lpm_mult0 mul_18x18(．dataa(a［17:0］)，．datab(b［17:0］)，．result(out_Pt0));

assign out_P0={2'b0，out_Pt0};

assign out_P1=a［18］? {2'b0，b［17:0］，18'b0}:38'b0;

assign out_P2=b［18］? {2'b0，a［17:0］，18'b0}:38'b0;

assign out_P3={1'b0，a［18］＆b［18］，36'b0};

assign out=out_P0+out_P1+out_P2+out_P3;

endmodule

5 结果

Karatsuba算法实现的尾数乘法运算的时序仿真如图3所示，图中p、q是输入的53 bit尾数，out和out2分别是Karatsuba算法和IP核乘法运算结果，可以看出两者结果相同。

图3 Karatsuba和IP核乘法结果比较Fig．3 Comparison of Karatsuba and IP nuclear multiplication results

采用QuatusII提供的IP核实现尾数乘法需要9个18 bit的乘法器及252个LUT，而采用Karatsuba算法(式(3))实现尾数乘法，只需要6个18 bit的乘法器，此外，还需要6个18 bit的加法器、3个36 bit的加法器和3个38 bit的减法器，若按照通常情况下一个N位加法器需要N个LUT来实现的话，那么该电路还需要6*18+3*36+3*38=330个LUT。如果将一个18 bit的乘法器用LUT实现需要437个LUT，因此，减少3个乘法器可以减少4*437=1 748个LUT。可以看出采用Karatsuba算法可以明显节省FPGA的资源，经仿真测试Karatsuba算法的乘法器相比于IP核的乘法器会增加大约11 ns的延时，如果采用流水线运算可以提高运算速度。

［1］ Jang J，Choi S，Prasanna V K K．Area and time efficient implementations of matrix multiplication on FPGAs［C］．2002 IEEE International Conference on Field Programmable Technology．Seoul，South Korea:IEEE，2002．

［2］ Akkas A，Schuhe M．A Quadruple precision and dual double precision floating-point multiplier［C］．Proc of Euromicro Symp Digital System Design(DSD＇03)，2003．

［3］ IEEE，IEEE standard floating-point arithmetic．IEEE Std 754-2008［S］．The Insitute of Electrical and Electronic Engineers，2008．

［4］ Karatsuba A．，Ofman Y．Multiplication of many-digital numbers by automatic computers［J］．Doklady Akad Nauk SSSR，1962，145(2):293-294．