斜井井间地震高斯射线束正演方法

魏峥嵘，李辉峰，范廷恩，李文洁

(1．西安石油大学地球科学与工程学院，陕西 西安710065;2．中海油研究总院，北京100027)

随着油田勘探开发的深入，尤其是现阶段非常规油气勘探的发展，要求进一步提高地震勘探的精度。井间地震方法可以有效地避免地面环境和表层低速带对高频地震信号的不利影响，可以接收到高信噪比的高频地震信息。同样由于观测系统的特殊性，使其可以获得多种类型的地震波，如反射波、透射波、折射波(首波)、直达波(初至波)以及管波等［1-2］。基于上述井间地震特点，井间地震勘探在油气勘探开发中具有非常重要的作用。

如今，油气开发技术已达到很高水平，用于开展井间地震勘探的井多为斜井、丛式井、水平井，若两井轨迹不在同一平面上，使得本为二维的井间地震问题变为了三维问题，如图1。

常规正演方法在精度上和速度上都不能很好地满足实际生产需要。射线追踪法包括试射法、弯曲法、波前法［3-4］，其优点在于简单直观，计算速度较快，所得地震波传播时间比较准确，但缺少地震波的动力学信息，而且对复杂地质构造会出现盲区［5］。波波动方程法虽然具有动力学特征，但是部分仅适用于简单的地质模型，且计算速度很慢，时效性差［6］。

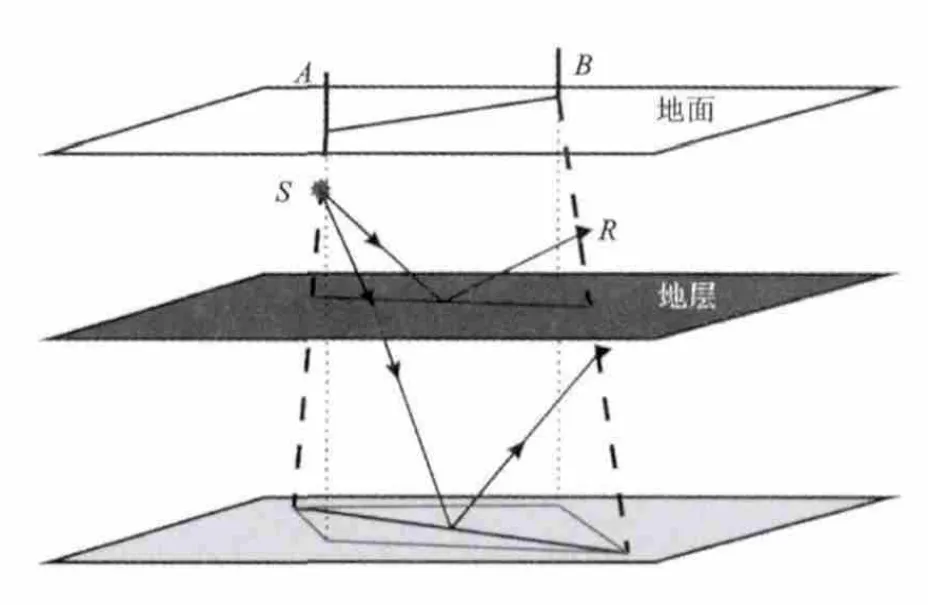
图1 不共面斜井三维示意图Fig．1 3D schematic diagram of non-coplanar inclined well

高斯射线束方法将波动方程法和射线追踪法很好地结合起来，其正演结果既有地震波的运动学特征又有动力学特征，且计算速度非常快。目前，高斯射线束正演方法仅用于地面地震及VSP正演，国内外尚未见到有关斜井井间地震高斯射线束正演的文献。本文在推导斜井井间地震高斯射线束正演算法的基础上，在VC和Qt环境下编制了斜井井间地震高斯射线束正演程序，利用该程序对多种斜井井间地质模型进行了正演，进而将本算法的结果与成熟的运动学正演和动力学正演结果进行对比，证实了本文算法的优越性。

1 斜井井间地震高斯射线束正演方法原理

高斯射线束正演是将波场分解到具有一定频率范围的射线束上实现地震波场的数值模拟，它是将动力学方程集中在射线附近的高频渐近时间调和解。高斯射线束正演包括运动学射线追踪、动力学射线追踪和波场叠加3个阶段。斜井井间地震高斯射线束正演如图2，从震源出发的高斯射线束就像一个以射线为中心的射线管，它的能量在中心射线附近呈高斯分布。检波点R处的波场就是由震源发出的多个射线束能量叠加得到的［5］。运动学射线追踪主要用来计算中心射线的运动轨迹，动力学射线追踪是将每条射线传播至接收井时能量的大小记录下来，最后通过波场叠加获得每一个检波点处能量的分布情况，把所有高斯射线束对检波点的贡献叠加形成最终的合成记录［6］。

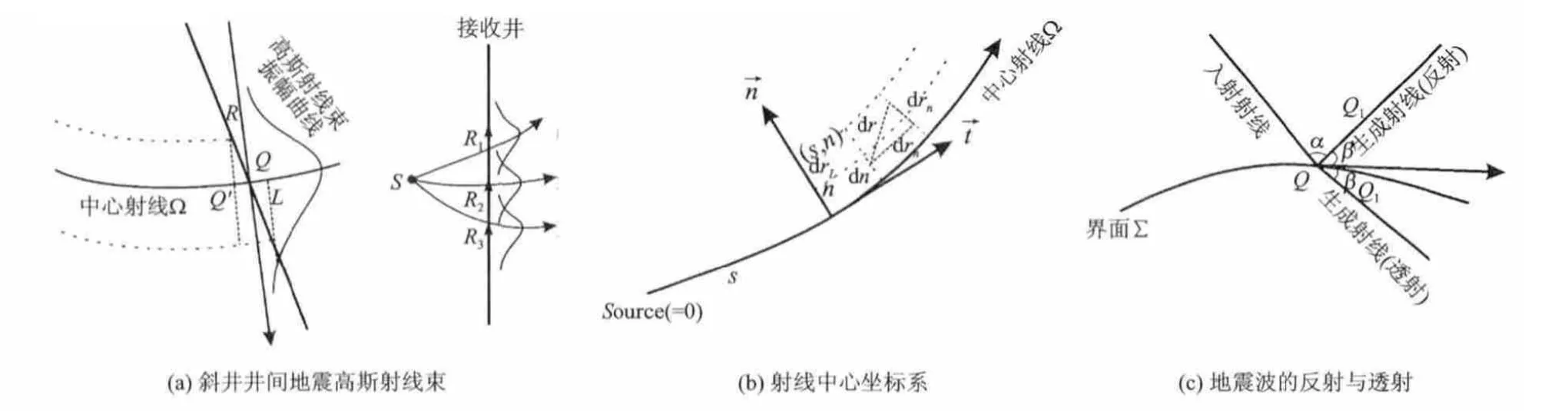
图2 斜井井间地震高斯射线束原理示意图Fig．2 Schematic diagram for the crosswell seismic Gaussian beam of inclined well

高斯射线束是指弹性动力学方程集中于射线附近的高频渐近时间调和解，该解在频率域具有如下表达形式

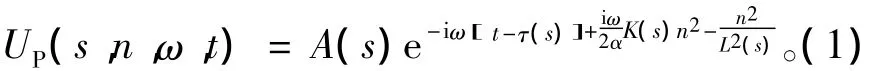
式中:ω 为圆频率;t为时间参量;UP(s，n，ω，t)是 P波位移［6］。

图2(b)中α(s)为波沿中心射线的传播速度。

射线的相前曲率

K(s)= α(s)Re［p(s)/q(s)］。

射线的有效半宽度

p(s)、q(s)为随着波沿射线的传播而变化的两复值函数，满足

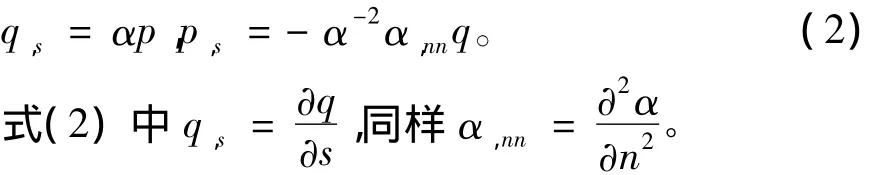
在式(1)中A(s)函数是指波沿中心射线的振幅。在层状模型中，假设射线从震源S0出发，穿过N个地层界面之后再反射回到接收点R处，振幅为

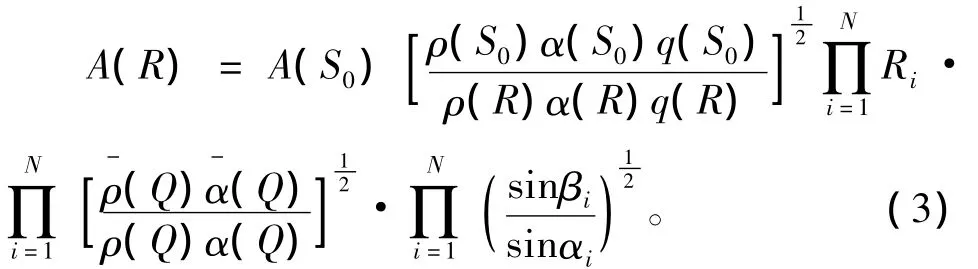
式中:Ri为界面的透射或者反射系数，Q为地震波与界面的交点，ρ为介质的密度，入射射线与生成射线与界面切线方向的夹角为αi和βi，如图2(c)所示。

除中心射线的距离n外另一个影响P波位移相位的是 s，在中心射线上，延时为 τ(s)=

从式(1)还可以得出沿射线的p、q还必须满足下列条件:q(s)≠0，使得

2 井间地震高斯射线束正演合成地震记录方法

通过高斯射线束运动学追踪，获得沿中心射线附近的波动方程高频近似P波位移分量在频率域的表达式，然后将所有射线在检波点处的能量叠加起来。因为弹性波动方程的线性性质，所以叠加近似满足波动方程

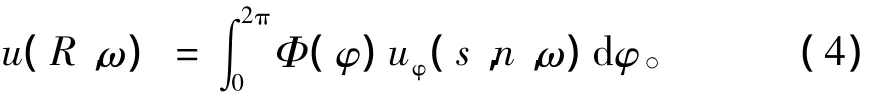
式中:uφ为初始入射角φ的高斯束位移(式(1));(s，n)为与射线有关的射线中心坐标系中接收点R的坐标;Φ(φ)为与初始入射角φ有关的权函数。

如果式(4)中Φ(φ)已知，那么根据该公式可以求出介质中任意一点的波场。用式(4)的渐近值与二维线源波动方程精确解的渐近值比较来确定Φ(φ)，

式中:α0为震源处的波速［6］。

使用高斯波包法来合成地震记录，假设震源函数为f(t)并且可积，其频谱为

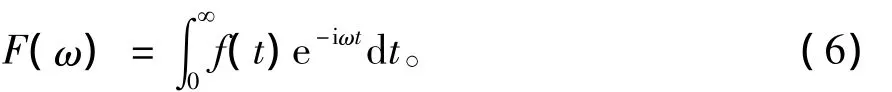
f(t)为高频函数时可以保证高斯射线束法的高频近似性。

设一子波函数

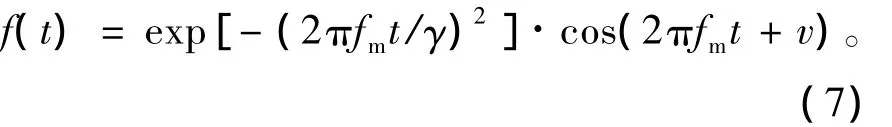
式中的fm，γ，v可根据需要选择，f(t)对应具有高斯包络的谐波载体，γ控制包络的宽度，fm为其主频率，该子波称作高斯包络子波。利用该子波形式，可以得到极端波包的近似表达式

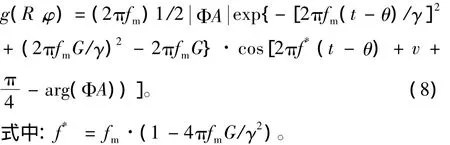
为了实现复杂情况下斜井井间地震高斯射线束正演，笔者在推导了基本方法的基础上，研制了复杂构造井间地震高斯射线束的正演算法，进而在Microsoft Visual Studio 6．0和 Qt环境下编写了程序［9-10］，程序流程见图3。

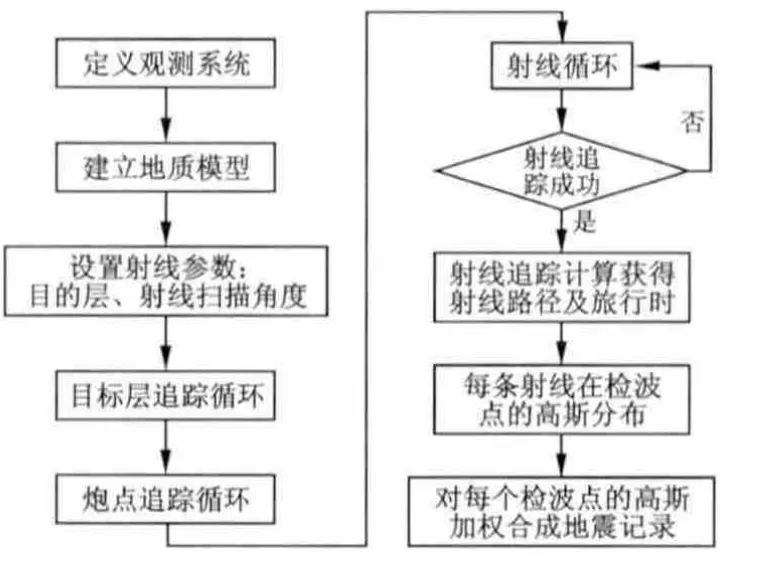
图3 井间地震高斯射线束正演算法流程Fig．3 Flow chart for the forward algorithm of crosswell seismic Gaussian beam

3 井间地震高斯射线束正演方法的实现及结果分析

3．1 模型试验

为了验证算法和程序的性能，笔者对多种地质模型进行了试算，限于篇幅这里仅列出逆断层模型(图4(a))的正演结果。

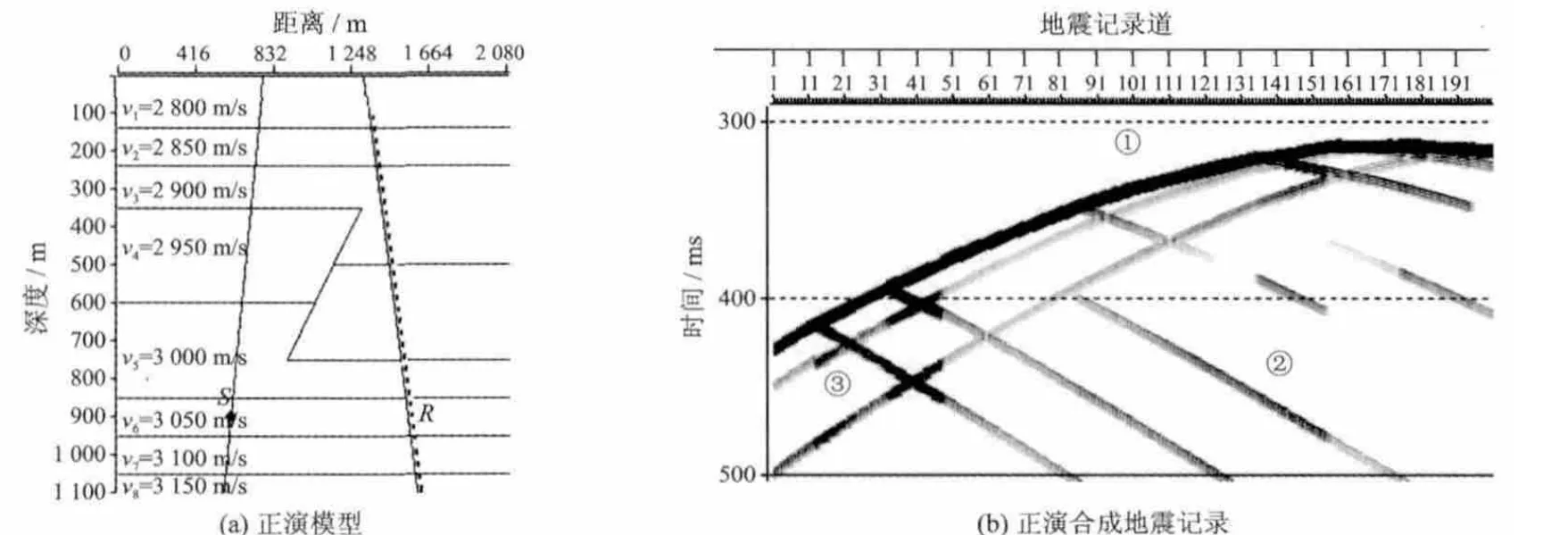
图4 斜井井间高斯射线束方法正演结果Fig．4 Forward result of crosswell seismic Gaussian beam of declined well

高斯射线束法正演的地震子波采用Gabor子波，子波主频250 Hz，采样间隔0．5 ms，观测系统为左井激发，右井接收，检波点数为200个，间隔5 m，激发位置见图4(a)，第一个检波点位于右井深度100 m处。

模型正演合成地震记录(图4(b))结果显示:(1)合成地震记录有透射波①、7组下行反射波②和2组上行反射波③，透射波与反射波时距曲线形态与理论计算相符。由于断层的存在，上行反射波时距曲线出现断开，能够准确反映断层模型运动学特征。(2)地震波能量和频率有明显的强、弱关系，具有明显的动力学特征。(3)单炮在PC2．2 GHz微机上正演平均用时为6 s。证明高斯射线束方法及所编程序同样适合斜井井间模型的正演模拟，能准确地表现出井间高斯射线束正演方法具有的运动学和动力学特征。

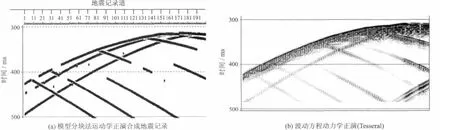
图5 斜井断层模型常规正演方法合成地震记录Fig．5 Synthetic seismograms of fault model of declined well using different forward methods

3．2 方法对比

为了体现本方法的正确性和优越性，笔者分别用模型分块法［11］运动学正演方法和Tesseral波动方程正演软件对图4所示的斜井井间地质模型进行了相同参数运动学和动力学正演。将所得结果进行了对比。以下图5(a)为模型分块法运动学正演合成地震记录，图5(b)为波动方程动力学正演合成地震记录。表1为3种正演方法单炮正演运算时间统计。

表1 单炮正演时间Tab．1 Single-shot forward time

高斯射线束法正演结果与图5(a)运动学正演结果对比显示，运动学正演因断层的存在有明显盲点，且频率和能量没有变化;与图5(b)波动方程动力学正演结果对比，可以看出动力学特征与其基本一致。因为动力学正演是全波场正演，且采用的子波不同，所以在合成地震记录上出现了多次波。表1单炮正演时间统计显示，高斯射线束方法用于斜井井间地震正演模拟的速度优于其他2种方法，时效性非常高。

3．3 斜井三维井间地震模型试验

图6为利用编写的三维建模软件实现的不共面斜井倾斜地层三维模型，炮点位于第三层，垂深500 m，2口斜井的轨迹在三维空间内不共面，这也是目前井间地震勘探的难点重点。通过对简单三维模型(图6(a))的实算，得出的地震波到达时与理论计算完全一致。在井不共面的情况下，检波点接收到的地层反射波和透射波分布于界面的某一范围，而不是在炮点与检波点连线在界面的投影上，因此，检波点接收到的射线数量有限。利用编写的程序正演得到的射线路径和合成地震记录显示，直达波及反射波时距曲线与共面斜井斜层相比会部分扭曲。在PC2．2 GHz微机上单炮正演平均用时为7 s，准确地表现出斜井井间高斯射线束正演方法具有的运动学和动力学特征。

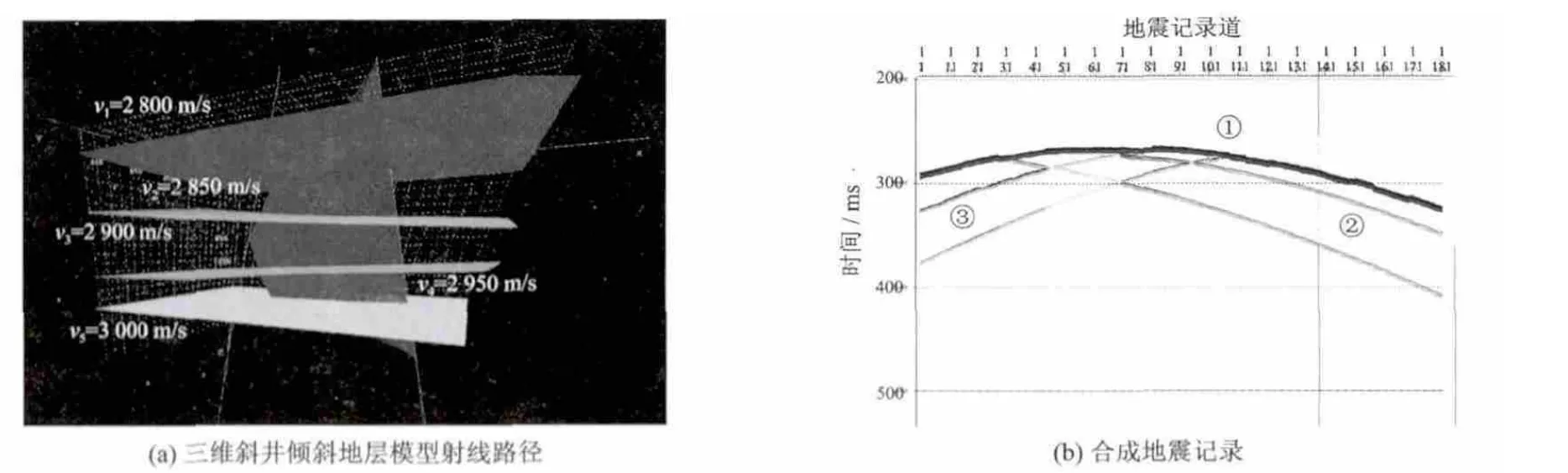
图6 三维斜井倾斜地层模型射线路径及合成地震记录Fig．6 Seam path and synthetic seismogram of tilt stratigraphic model of 3D declined well

4 结论

斜井井间地震高斯射线束正演方法能够正确反映斜井井间地震地震波的运动学特征，并且具有十分清楚的地震波动力学特征，能够清晰地反映地震波在介质中的传播规律。所得结果与理论相符，证明该方法及所编软件适用于斜井井间地震正演模拟，并且正演速度快，在斜井井间地震勘探开发领域有非常好的应用前景。

［1］ 何惺华．井间地震［M］．北京:石油工业出版社，2008:1-8，54-138．

［2］ 徐峰．地震勘探新技术［M］．北京:石油工业出版社，2009:148-156，191-200．

［3］ 邓飞，刘超颖．三维射线快速追踪及高斯射线束正演［J］．石油地球物理勘探，2009，44(2):158-165．DENG Fei，LIU Chao-ying．3-D rapid ray-tracing and Gaussian ray-beam forward simulation［J］．Oil Geophysical Prospecting，2009，44(2):158-165

［4］ 张钋，刘洪，李幼铭．射线追踪方法的发展现状［J］．地球物理学进展，2000，15(1):36-45．ZHANG Po，LIU Hong，LI You-ming．The situation and progress of ray tracung method research［J］．Progress In Geophysics，2000．3，15(1):36-45．

［5］ 窦玉坦，郭常升，毛中华，等．井间地震波动方程正演数值模拟及其应用［J］．地球物理学进展，2007，22(6):1867-1872．DOU Yu-tan，GUO Chang-sheng，MAO Zhong-hua，et al．The wave equation forward numerical simulation and application in crosswell seismic［J］．Progress in Geophysics，2007，22(6):1867-1872．

［6］ Cerveny V．Synthetic body wave seisnograms for laterally varying structures by the Gaussian beam method［J］．Geophys，1983，73:389-426．

［7］ Ross N Hill．Gaussian beam migration［J］．Geophysics，1990，55:1416-1428．

［8］ 周熙襄，刘学才，蒋先艺．二维高斯射线束地震模型［J］．石油地球物理勘探，1991，26(4):452-464．ZHOU Xi-xiang，LIU Xue-cai，JIANG Xian-yi．Seismic model made by two-dimensional Gaussian beam method［J］．Oil Geophysical Prospecting，1991，26(4):452-464．

［9］ David Kincaid，Ward Cheney．数值分析［M］．王国荣，译．北京:机械工业出版社，2005:276-296．

［10］William H Press，Saul A Teukolsky．C 数值算法［M］．傅祖芸，赵梅娜，译．北京:电子工业出版社，2004:92-95．

［11］徐果明，卫山，高尔根，等．二维复杂介质的块状建模及射线追踪［J］．石油地球物理勘探，2001，36(2):213-219．XU Guo-ming，WEI Shan，GAO Er-gen，et al．Block model building and ray-tracing in 2-D complicated medium［J］．Oil Geophysical Prospecting，2001，36(2):213-219．