盐岩非线性Burgers 模型及其参数识别

王军保 ，刘新荣 ，杨欣，黄明

(1. 西安建筑科技大学 土木工程学院，陕西 西安，710055；2. 重庆大学 土木工程学院，重庆，400045；3. 福州大学 土木工程学院，福建 福州，350108)

盐岩是一种特殊的软岩，具有结构致密、孔隙度低、渗透性低、力学性质稳定、蠕变性良好和损伤自恢复能力强等诸多优点，被公认为是能源(石油、天然气)地下储存和放射性废弃物地下处置的理想介质[1]。蠕变特性作为盐岩最为重要的力学性质之一，是影响盐岩地下储存库长期稳定性、安全性以及可用性的关键因素：因此，对盐岩蠕变特性进行研究尤为重要。由于盐岩在能源地下储存方面的重要地位，近年来国内外学者对盐岩蠕变本构关系进行了较多研究，提出了多种蠕变模型[1-9]。但总体上，这些模型可以分为以下三大类[10]：经验模型、唯象模型和元件组合模型。从整个岩石力学流变领域来看，元件组合模型由于本构方程形式简单，模型及其参数物理意义明确，且能够把岩石复杂的力学性质直观地表现出来，因而应用较为广泛。但传统的元件组合模型是一种线性模型，无法描述岩石蠕变的非线性特征。为了克服这一不足，一种有效的方法就是采用非线性流变元件代替常规线性流变元件，并据此建立岩石蠕变模型。熊良宵等[11]提出了一个可以描述岩石非线性黏弹性流变特征的黏滞体，将该非线性黏滞体替换Burgers 模型中的线性黏滞体，得到了非定常 Burgers 模型。黄明等[12]提出了一种修正Kelvin 模型，并将该模型与黏滞体、弹性体进行串联建立了可描述岩石非线性蠕变特性的修正Burgers 模型。康永刚等[13]为了描述岩石蠕变全过程，用非定常黏滞体替换Burgers 模型中的定常黏滞体，给出了一种非定常Burgers 模型。Steipi 等[14]将西原模型中的黏塑性参数描述为黏塑性应变的函数，提出了改进的西原模型。蒋昱州等[15]提出了一个变系数的黏滞体，建立了新的岩石非线性黏弹塑性全过程蠕变模型。杨文东等[16]构建了由弹性体、村山体、非线性黏塑性体串联而成的非线性黏弹塑性流变模型，该模型可以描述岩石流变的加速阶段。曹平等[17]定义应力与试件长期强度的比值为加速蠕变速率幂级数n，模型发生加速蠕变时的总蠕变量为蠕变特征长度 εc，进而建立了能够描述岩石加速蠕变的力学模型。以往对于岩石非线性蠕变模型的研究大多是针对岩石加速蠕变阶段展开的，而岩石特别是盐岩，在前2 个蠕变阶段也存在非线性特征，且在围压作用下，盐岩加速蠕变并不容易出现[1]。基于此，本文作者结合非线性流变力学理论，对常规黏滞体元件进行改进，提出一种变系数非线性黏滞体，然后通过将该非线性黏滞体替换常规Burgers 模型中的线性黏滞体，建立一种非线性Burgers 模型即NBurgers 模型，并利用盐岩三轴压缩蠕变试验结果对NBurgers 模型参数进行反演识别，以验证模型的适用性。

1 非线性黏滞体的提出及其特性分析

传统的元件组合模型通常无法反映岩石蠕变的非线性特征，这是因为这类模型将黏性元件假定为理想的牛顿流体，认为其黏性系数是固定不变的常数的缘故[15]。近年来，随着人们对岩石非线性蠕变特征的逐步研究和认识，发现这一假定不够准确，岩石材料的黏滞系数在蠕变过程中是不断发生变化的。陈文玲等[18]通过对岩石蠕变过程的分析，指出当施加的荷载为中高应力水平但未达到岩石破坏应力时，岩石蠕变仅出现前2 个阶段，即衰减蠕变阶段和稳态蠕变阶段，此时，黏滞系数随着时间增加而逐渐增大，并最终达到一个稳定值后不再变化。

受此启发，为了更好地描述盐岩的非线性蠕变特征，本文提出一个变系数的非线性黏滞体，其本构关系如下：

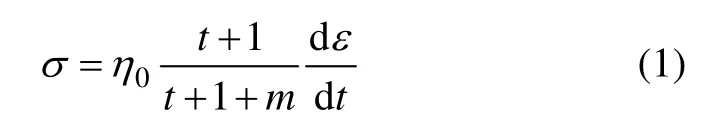
式中：σ 为应力；dε/dt为应变速率；t 为时间；m 为非线性系数；η0为黏滞系数的最大值。

从式(1)可以看出该黏滞体的黏滞系数随时间增加不断发生变化，且其变化规律符合下式：

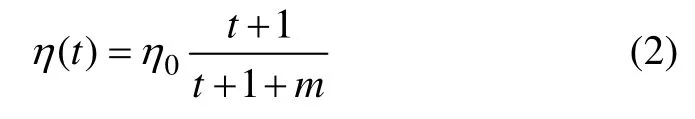
下面对式(2)函数特点进行分析。

当t=0 时，

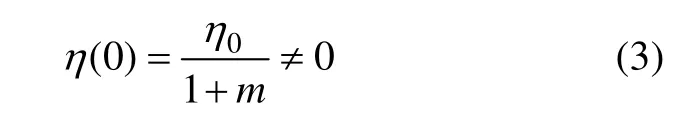
即 η (t)初始值不为0。

将式(2)对时间求导数并整理，可得

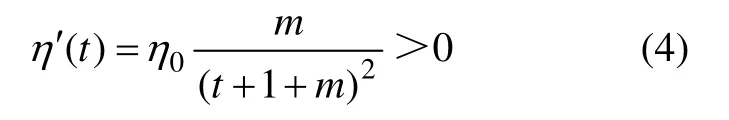
说明η (t)单调递增。

将式(2)变形可得

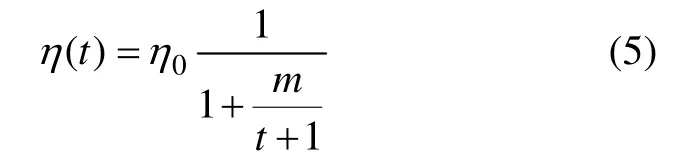
由式(5)可知：当t→∞时，η (t)→η0，这说明η (t)存在上限值且上限值为η0。

由以上分析可以看出：当时间t 从0→∞时，黏滞系数η (t)从η0/(1+m)→η0。因此，式(2)所示函数特点与文献[18]所描述的岩石黏滞系数随时间的变化规律较符合。

式(1)变形可得

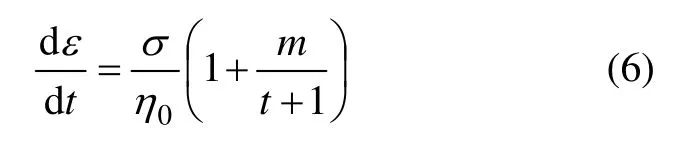
将式(6)对时间积分，并结合初始条件(t=0，ε=0)，可得该非线性黏滞体的蠕变方程为

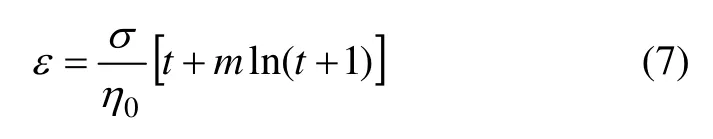
1.1 非线性系数对蠕变应变的影响

图1 所示为σ和η0均相同的情况下，非线性系数m 的变化对蠕变曲线的影响规律示意图。由图1可以看出：当m=0时，此时实质为常规黏滞体，蠕变曲线为斜率不变的直线，仅存在稳态蠕变阶段；当m≠0时，蠕变曲线不再是直线，而是一簇形状相似的曲线簇，且均存在衰减蠕变和近似稳态蠕变2 个阶段。随着m 增大，衰减蠕变阶段越来越明显，持续时间越来越长，进入稳态蠕变的时间越来越晚，且相同时刻的变形量也越来越大。这说明非线性黏滞体具有衰减蠕变特性，与常规黏滞体不同。

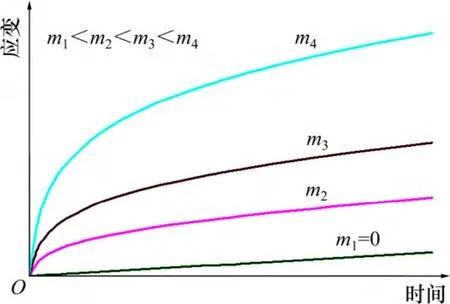
图1 不同非线性系数下的蠕变曲线Fig.1 Creep curves with different nonlinear coefficients

1.2 非线性系数对蠕变速率的影响

式(6)所示为非线性黏滞体蠕变速率的表达式。由式(6)可知：m=0时，此时实质为常规黏滞体，蠕变速率保持σ/η0不变；m≠0时蠕变速率随时间增加而单调递减，且当t=0时，dε/dt=σ(1+m)/η0；当t→∞时，dε/dt=σ/η0。这说明非线性黏滞体的初始蠕变速率为常规黏滞体蠕变速率的(1 + m)倍，且只有当t→∞时，2 种黏滞体的蠕变速率才相等，其余时刻非线性黏滞体的蠕变速率均大于常规黏滞体的蠕变速率。

图2 所示为不同非线性系数下的蠕变速率曲线示意图。由图2 可见：当m=0时，蠕变速率最小且保持恒定，蠕变速率曲线为1 条水平线；当m≠0时，蠕变速率在初始时刻最大，随着时间延长而逐渐衰减，且m 越大衰减过程越显著。理论上，只有当t→∞时，非线性黏滞体和常规黏滞体的蠕变速率才会相等；而实际上，由于非线性系数m 是1 个有限值，当时间增加到一定程度后，m/(t+1)已经接近于0，此时两者的蠕变速率已经非常接近。图2 所示曲线可以清楚地说明这一点。

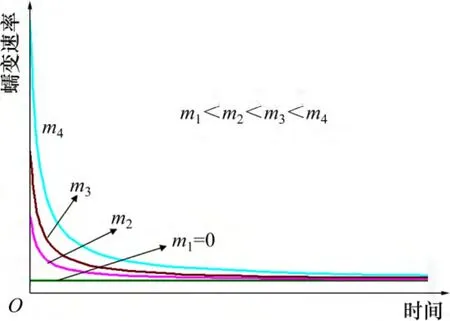
图2 不同非线性系数下的蠕变速率曲线Fig.2 Creep rate curves with different nonlinear coefficients

由以上分析可以看出：非线性黏滞体不仅包含了常规黏滞体的基本特性，而且还具有常规黏滞体所不具有的特殊性质。因此，在描述盐岩蠕变特性时将会具有更好的适应性。

2 盐岩蠕变试验及非线性蠕变模型

2.1 盐岩蠕变试验

试验所用盐岩试样取自江苏淮安某盐矿，主要成分为NaCl，质地较纯，呈白色、灰白色，部分略带灰黑色不溶物杂质。按照岩石力学试验标准的要求，将岩样加工成直径为50 mm、高度为100 mm 的圆柱形标准试件。试验仪器采用长春朝阳仪器厂生产的RLW-2000 岩石流变试验机。该设备主要由机架、轴向稳压系统、侧向稳压系统、数字控制系统及微机系统等5 部分组成，最大轴向荷载为2 000 kN，最大围压为60 MPa。

为了研究该矿盐岩的蠕变特性，对4 个试件进行不同围压下的分级加载蠕变试验。图3 所示为围压10 MPa 试件的分级加载蠕变试验曲线，轴向应力分别为20，25 和30 MPa。由图3 可以看到：盐岩在各级荷载作用下的变形均由加载过程产生的瞬时应变、衰减蠕变应变以及蠕变速率较为稳定的稳态蠕变应变3部分组成。由于试验所施加的最高应力未达到使岩样发生加速蠕变的临界应力，且受试验条件限制，加载时间不够长，盐岩未进入到加速蠕变阶段；在围压不变的情况下，随着轴向应力增大，盐岩瞬时应变、蠕变应变、稳态蠕变速率等均随之增大，且轴向应力越大，衰减蠕变阶段蠕变曲线的曲率半径越大，经历的时间越长，达到稳态蠕变的时间越晚。

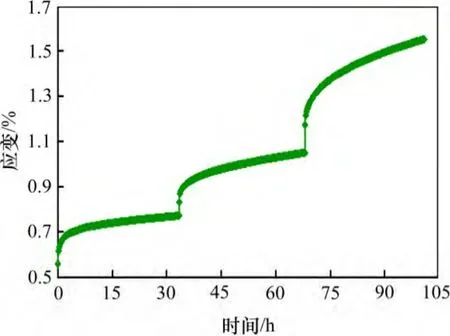
图3 盐岩分级加载蠕变试验曲线Fig.3 Creep curve of salt rock under step loading

2.2 非线性蠕变模型的建立

通过前面对盐岩蠕变曲线特征的分析可以看出，试验曲线与Bugrers 模型蠕变曲线较为相似，但常规Bugrers 模型无法反映盐岩蠕变的非线性特征。为了能够较好地描述盐岩的非线性黏弹性蠕变特性，本文将前面提出的非线性黏滞体替换常规Bugrers 模型中的线性黏滞体，从而构成变系数的非线性Burgers 模型，本文将其命名为NBurgers 模型。NBurgers 模型由弹性体(H)、非线性黏滞体(NN)和非线性黏弹性体(NN/H)共3 部分串联组成。考虑到参数数量过多会给模型参数求解增加难度，本文取NN 体的非线性系数m1和NN/H 体的非线性系数m2为同一值，且均以m 来表示。模型示意图见图4。

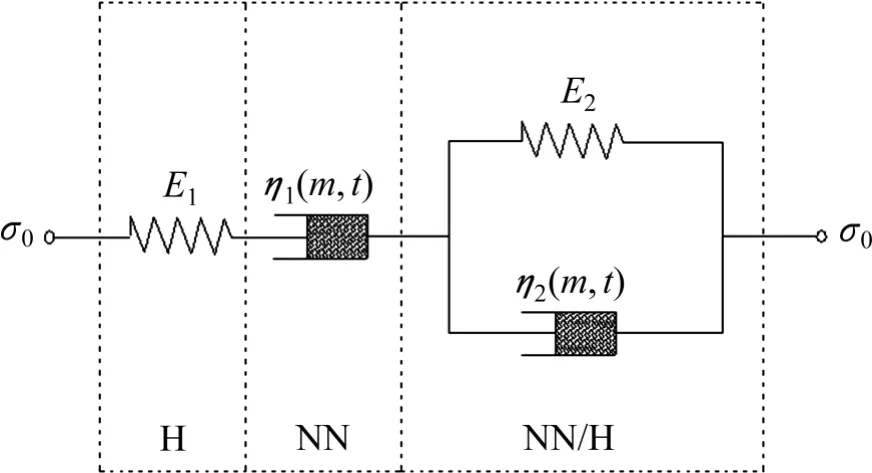
图4 NBurgers 模型示意图Fig.4 Schematic view of NBurgers model

在该模型中，假定弹性体的变形为 εe，非线性黏滞体的变形为 εnv，非线性黏弹性体的变形为 εnve，则模型总变形可表示为

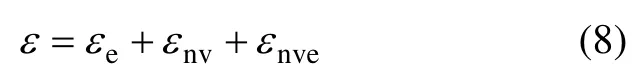
假定在t=0时，施加瞬间应力σ=σ0，则有

(1) 弹性体(H)的本构关系为

式中：E1为弹性模量。

(2) 非线性黏滞体(NN)中，结合式(7)可得其蠕变方程为

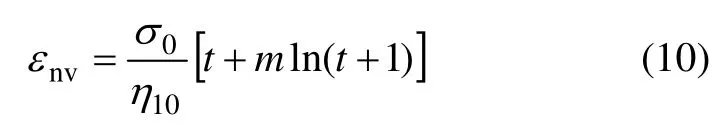
(3) 非线性黏弹性体(NN/H)中，结合常规Kelvin模型，可得其本构方程为

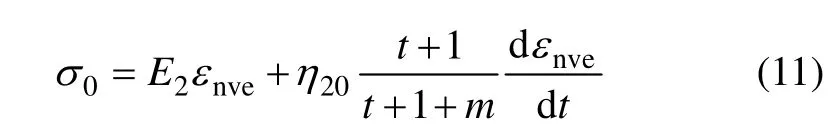
式中：E2为黏弹性模量。

将式(11)变形为

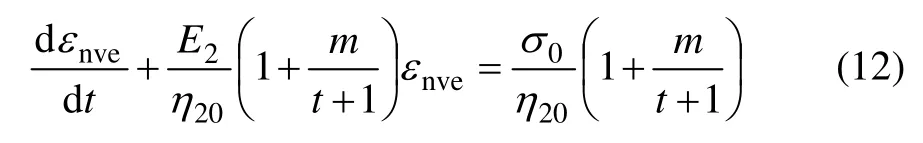
对式(12)解微分方程，可得

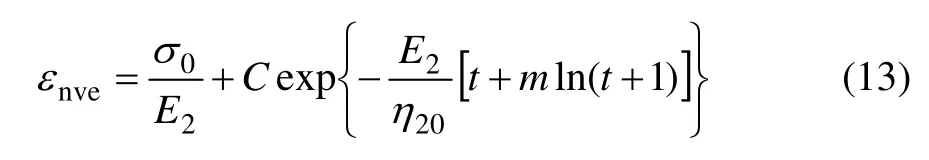
式中：C 为积分常数。

对于非线性黏弹性体(NN/H)来说，当t=0时，εnve=0。对式(13)代入初始条件，则可解得

将C 代入式(13)可得非线性黏弹性体的蠕变方程为

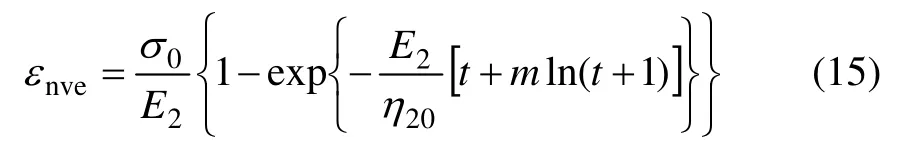
由于模型中3 部分串联，根据式(8)，NBurgers 模型在一维应力状态下的蠕变方程可写为

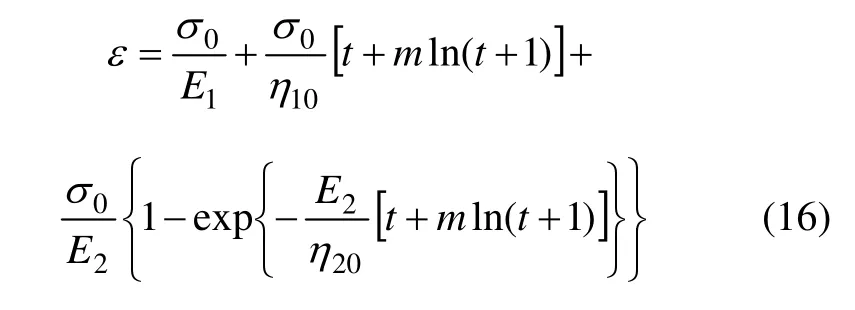
在三维应力状态下，盐岩内部应力张量 σij可以分解为应力球张量 σm和应力偏张量 Sij，应变张量 εij分解为应变球张量 εm和应变偏张量 eij。根据广义虎克定律，则有

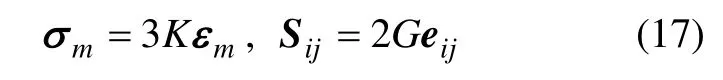
其中

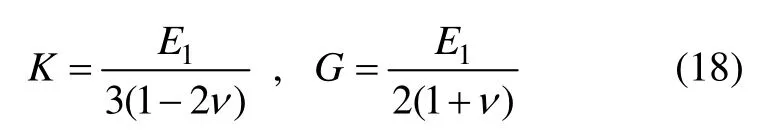
式中：K 为体积模量；G 为剪切模量；ν 为泊松比。

假定盐岩为各向同性材料，其蠕变变形仅由应力偏张量引起，且在蠕变过程中盐岩泊松比不随时间变化[16]，则在三维应力状态下，考虑σ2=σ3，NBurgers模型的轴向蠕变方程为

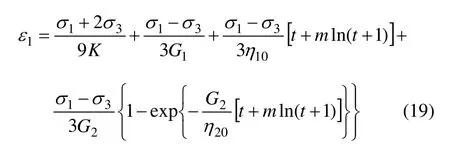
在三维应力状态下，当σ2=σ3时，Burgers 模型的轴向蠕变方程为[11]

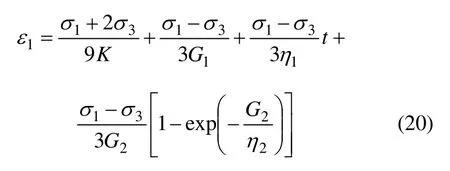
对比式(19)和式(20)可以看出：当非线性系数m=0时，NBurgers 模型退化为常规Burgers 模型。因此，常规Burgers 模型是本文非线性模型在m=0时的一种特例。

3 盐岩非线性蠕变模型参数识别

为了对NBurgers 模型进行参数识别，首先将图3所示盐岩分级加载蠕变曲线进行处理，得到了不同轴压时的单级蠕变曲线(图5 中散点曲线)。

最小二乘法是确定岩石蠕变参数应用较为广泛的一种方法。本文根据盐岩蠕变试验结果，基于非线性最小二乘法基本原理，利用1stOpt 软件，采用自定义函数的方法，对式(19)所示NBurgers 模型参数进行反演识别。具体方法及过程如下。

(1) 以待反演的蠕变参数作为设计变量，即

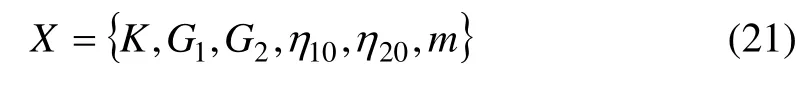
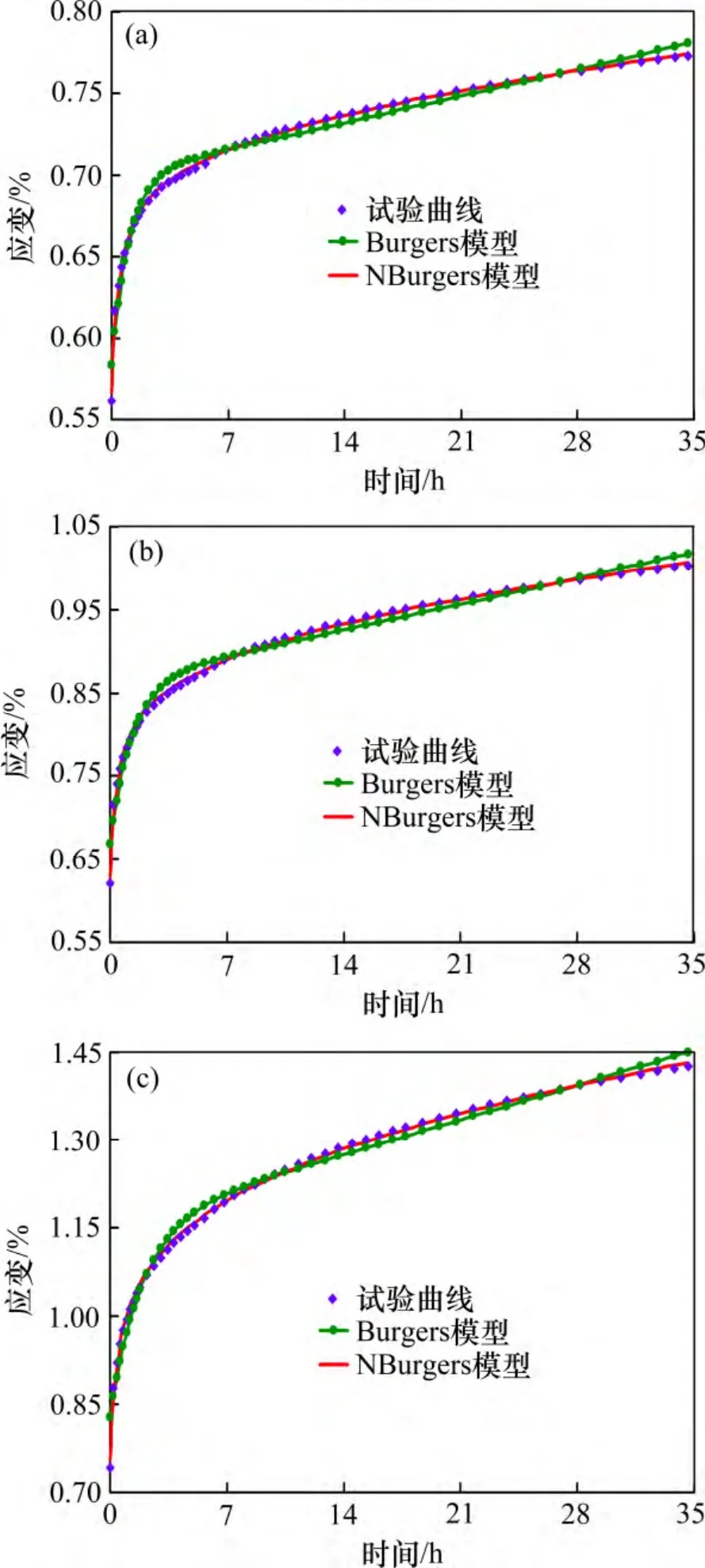
图5 拟合曲线和试验曲线对比图Fig.5 Comparison between fitting curves and test curves

式中：K 和G1可根据式(18)转变为确定弹性模量E1，盐岩泊松比取ν=0.3。

(2) 取设计变量如式(21)所示，建立目标函数

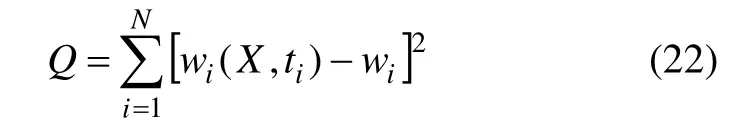
式中：N 为试验数据组数；wi(X,ti)为t 时刻计算变形值；wi为t 时刻试验实测变形值。

(3) 设定目标函数Q 的控制精度并进行参数迭代求解。若Q 满足精度要求，则停止迭代，输出计算结果；若不满足，则继续迭代，直到满足精度要求为止。

参数反演结果见表1。图5 给出了NBurgers 模型拟合曲线与试验曲线的对比情况。图5 同时给出了采用常规Burgers 模型对试验数据的拟合情况。

从表1 和图5 可以看到：NBurgers 模型拟合效果良好，相对误差较小，拟合值非常逼近于试验值，且其与试验值的吻合程度要明显比常规Burgers 模型的高，说明NBurgers 模型能够更好地描述盐岩的黏弹性蠕变特性，具有一定的适用性。

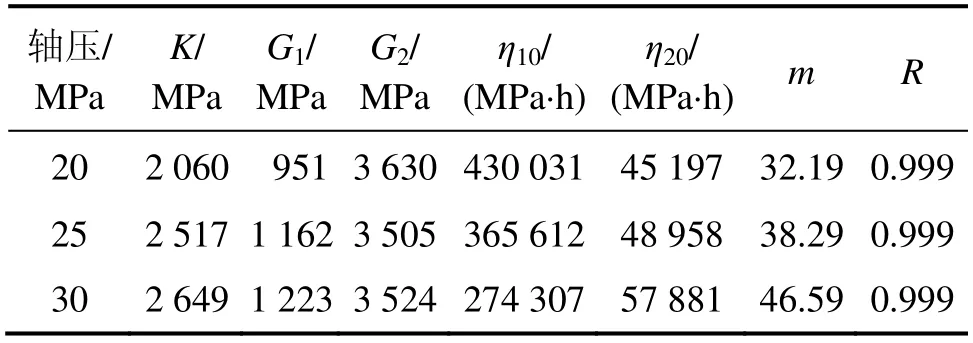
表1 NBurgers 模型参数反演结果Table 1 Creep parameters of NBurgers model

4 结论

(1) 基于非线性流变力学理论，对常规黏滞体元件进行了改进，提出了一种变系数的非线性黏滞体，并对其特性进行了分析。分析表明，由于非线性系数的引入，改进后的非线性黏滞体在描述岩石蠕变特性时具有更好的适应性。

(2) 将非线性黏滞体替换常规Burgers 模型中的线性黏滞体，建立了非线性Burgers 模型，即NBurgers模型。该模型在一定条件下可退化为常规Burgers模型。

(3)对盐岩试件开展了三轴压缩蠕变试验，并利用试验结果对模型参数进行了反演识别。拟合曲线和试验曲线对比显示，NBurgers 模型拟合曲线和试验曲线的吻合程度要明显高于常规Burgers 模型，说明该模型能够更好地描述盐岩的黏弹性蠕变特性。

[1] 杜超, 杨春和, 马洪岭, 等. 深部盐岩蠕变特性研究[J]. 岩土力学, 2012, 33(8): 2451-2456.DU Chao, YANG Chunhe, MA Hongling, et al. Study of creep characteristics of deep rock salt[J]. Rock and Soil Mechanics,2012, 33(8): 2451-2456.

[2] Chan K S, Brodsky N S, Fossum A F, et al. Damage-induced non-associated inelastic flow in rock salt[J]. International Journal of Plasticity, 1994, 10(6): 623-642.

[3] HOU Zhengmeng. Mechanical and hydraulic behaviour of salt in the excavation disturbedzone around underground facilities[J].International Journal of Rock Mechanic and Mining Science,2003, 40(5): 725-738

[4] Jin J, Cristescu N D. An elastic/viscoplastic model for transient creep of rock salt[J]. International Journal of Plastic, 1998,14(1/2/3): 85-107.

[5] WANG Guijun. A new constitutive creep-damage model for salt rock and its characteristics[J]. International Journal of Rock Mechanic and Mining Science, 2004, 41(Supp 1): 61-67.

[6] ZHOU Hongwei, WANG Chunping, Han B B, et al. A creep constitutive model for salt rock based on fractional derivatives[J].International Journal of Rock Mechanics and Mining Sciences,2011, 48(1): 116-121.

[7] 李萍, 邓金根, 孙焱, 等. 川东气田盐岩、膏盐岩蠕变特性试验研究[J]. 岩土力学, 2012, 33(2): 444-448.LI Ping, DENG Jingen, SUN Yan, et al. Experimental study of creep characteristics of rock gypsum-salt and rock salt in Chuandong gas field[J]. Rock and Soil Mechanics, 2012, 33(2):444-448.

[8] 郤保平, 赵阳升, 赵延林, 等. 含高盐份泥岩夹层的盐岩蠕变特性研究[J]. 地下空间与工程学报, 2007, 3(1): 23-26.XI Baoping, ZHAO Yangsheng, ZHAO Yanlin, et al. Study on creep property of rock salt with mudstone interlayer[J]. Chinese Journal of Underground Space and Engineering, 2007, 3(1):23-26.

[9] 刘江, 杨春和, 吴文, 等. 盐岩蠕变特性和本构关系研究[J].岩土力学, 2006, 27(8): 1267-1271.LIU Jiang, YANG Chunhe, WU Wen, et al. Study on creep characteristics and constitutive relation of rock salt[J]. Rock and Soil Mechanics, 2006, 27(8): 1267-1271.

[10] 吴文, 杨春和, 侯正猛. 盐岩中能源(石油和天然气)地下储存力学问题研究现状及其发展[J]. 岩石力学与工程学报, 2005,24(增2): 5561-5568.WU Wen, YANG Chunhe, HOU Zhengmeng. Investigation on studied situations associated with mechanical aspects and development for underground storage of petroleum and natural gas in rock salt[J]. Chinese Journal of Rock Mechanics and Engineering, 2005, 24(Supp 2): 5561-5568.

[11] 熊良宵, 杨林德, 张尧. 岩石的非定常Burgers 模型[J]. 中南大学学报(自然科学版), 2010, 41(2): 679-684.XIONG Liangxiao, YANG Linde, ZHANG Yao. Non-stationary Burgers model for rock[J]. Journal of Central South University(Science and Technology), 2010, 41(2): 679-684.

[12] 黄明, 刘新荣. 三峡库区泥质粉砂岩非线性蠕变模型辨识[J].岩石力学与工程学报, 2011, 30(增2): 3804-3810.HUANG Ming, LIU Xinrong. Research on nonlinear creep model identification of siltite in three Gorges reservoir area[J].Chinese Journal of Rock Mechanics and Engineering, 2011,30(Supp 2): 3804-3810.

[13] 康永刚, 张秀娥. 基于Burgers 模型的岩石非定常蠕变模型[J].岩土力学, 2011, 32(增1): 424-427.KANG Yonggang, ZHANG Xiue. A non-stationary model for rock creep based on Burgers model[J]. Rock and Soil Mechanics,2011, 32(Supp 1): 424-427.

[14] Steipi D, Gioda G. Visco-plastic behaviour around advancing tunnels in squeezing rock[J]. Rock Mechanics and Rock Engineering, 2009, 42(2): 319-339.

[15] 蒋昱州, 张明鸣, 李良权. 岩石非线性黏弹塑性蠕变模型研究及其参数识别[J]. 岩石力学与工程学报, 2008, 27(4):832-839.JIANG Yuzhou, ZHANG Mingming，LI Liangquan. Study on nonlinear viscoelasto-plastic creep model of rock and its parameter identification[J]. Chinese Journal of Rock Mechanics and Engineering, 2008, 27(4): 832-839.

[16] 杨文东, 张强勇, 陈芳, 等. 辉绿岩非线性流变模型及蠕变加载历史的处理方法研究[J]. 岩石力学与工程学报, 2011, 30(7):1405-1413.YANG Wendong, ZHANG Qiangyong, CHEN Fang, et al.Research on nonlinear rheological model of diabase and treatment for creep loading history[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(7): 1405-1413.

[17] 曹平, 刘业科, 蒲成志, 等. 一种改进的岩石黏弹塑性加速蠕变力学模型[J]. 中南大学学报(自然科学版), 2011, 42(1):142-146.CAO Ping, LIU Yeke, PU Chengzhi, et al. An improved accelerated creep mechanical model of viscoelasto-plastic rock[J]. Journal of Central South University (Science and Technology), 2011, 42(1): 142-146.

[18] 陈文玲, 赵法锁, 弓虎军. 三轴蠕变试验中云母石英片岩蠕变参数的研究[J]. 岩石力学与工程学报, 2011, 30(增 1):2810-2816.CHEN Wenling, ZHAO Fasuo, GONG Hujun. Study of creep parameters of mica-quartzoseschist during triaxial creep test[J].Chinese Journal of Rock Mechanics and Engineering, 2011,30(Supp 1): 2810-2816.