基于局部加密等级网格的2.5D 直流电法有限元模拟

胡宏伶，肖晓，潘克家 ，汤井田，谢维

(1. 湖南师范大学 数学与计算机科学学院，湖南 长沙，410081;2. 中南大学 地球科学与信息物理学院，有色金属成矿预测教育部重点实验室，湖南 长沙，410083;3. 中南大学数学与统计学院, 湖南 长沙，410083;4. 成都理工大学 油气藏地质及开发工程国家重点实验室, 四川 成都，610059)

自1971 年Coggon[1]将有限单元法(finite element method，FEM)应用到直流电阻率法数值模拟以来，FEM 以其理论完备、边界处理能力强和通用性强等优点，在直流电法正演中得到了广泛应用[2-18]。直流电法数值模拟问题具有如下特点：地下往往存在复杂的电性不均匀结构，电性差异可达几个数量级；研究区域具有无界性，需要进行截断边界处理；点电源处电位为无穷大，具有奇性。这些都将导致传统有限元法模拟精度及效率降低。为解决上述问题，提高有限元的计算效率及点源处的模拟精度，汤井田等[19]提出一种3D 直流电阻率有限元—无限元耦合数值模拟方法，有效地降低了截断边界的影响。为提高源点附近的精度，陈小斌等[20]采用组合网格技巧，对源点附近进行局部加密，并利用有限元直接迭代算法求解线源频率域大地电磁正演问题。汤井田等[21-24]采用非结构化网格的自适应有限元，通过加密奇点(点电源)处网格密度以减小有限元的计算误差，提高了有限元模拟的速度和精度。采用局部加密的非结构化网格，能提高奇点附近有限元的模拟精度，但网格剖分及总体刚度矩阵集成繁琐，编程较复杂，且网格剖分具有很大的不确定性。非结构化网格破坏了FEM 固有的许多超收敛结构，在提高局部精度的同时降低了FEM 的整体收敛速度[25]。另一种处理方式是采用较密的均匀剖分，并利用多网格法求解超大规模有限元方程。为解决通常几何多重网格法粗网格难以模拟复杂电性差异的问题，Moucha 等[26]提出一种电导率的6 参数化表示法，并给出基于9 点格式有限差分的多网格法，求解2D 直流电法正演问题；鲁晶津等[27]提出直流电阻率3D 正演的代数多重网格方法。潘克家等[28-29]引入外推瀑布式多网格法求解2.5D/3D 直流电阻率法数值模拟问题，大大提高了直流电法正演的计算速度。Li等[30]提出一种3D 直流电法的多源系统有限元模拟方案。Wang 等[31]给出非结构化网格下各向异性3D 直流电阻率法有限元模拟。在此，本文作者拟结合局部加密策略和结构化网格的优点，提出一种基于λ-等级网格的2.5D 直流电法有限元模拟方案。

1 电阻率法2.5D 有限元逼近

1.1 点源稳定电场边值问题

假设地下为2D 构造，以电源点为坐标原点建立合适坐标系使z 轴平行于构造走向，结合z 方向的Fourier 变换，点源波数域中电位函数 U (x, y , k)在Ω内满足如下2D 变系数非齐次亥姆霍茨(Helmholtz)方程边值问题[16]：

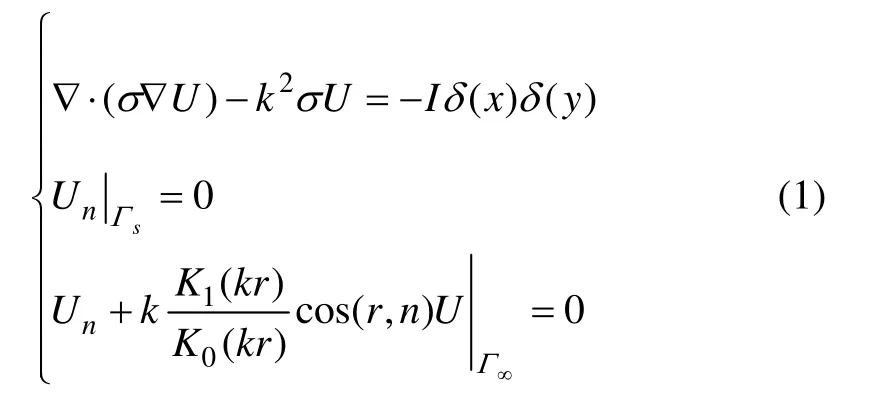
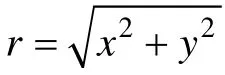
考虑到本文将采用局部加密的等级网格，截断边界Γ∞取为如图1 所示以原点为圆心、r∞为半径的半圆，则电位u 满足的椭圆边值问题(1)可进一步简化为

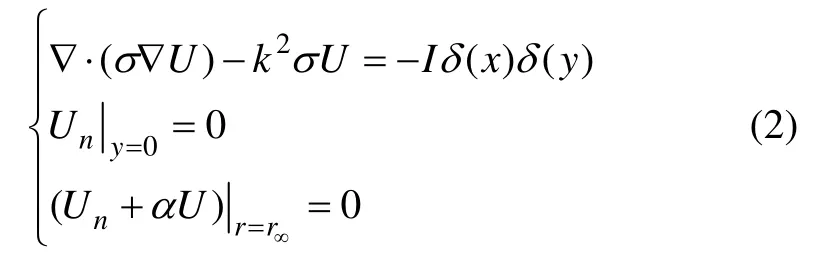
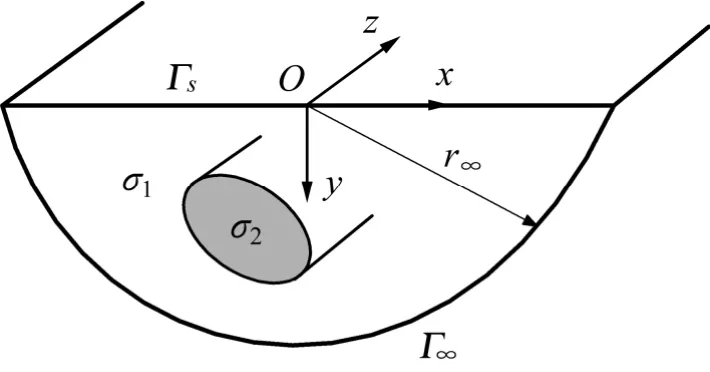
图1 2D 结构模型Fig.1 Model of 2D structure

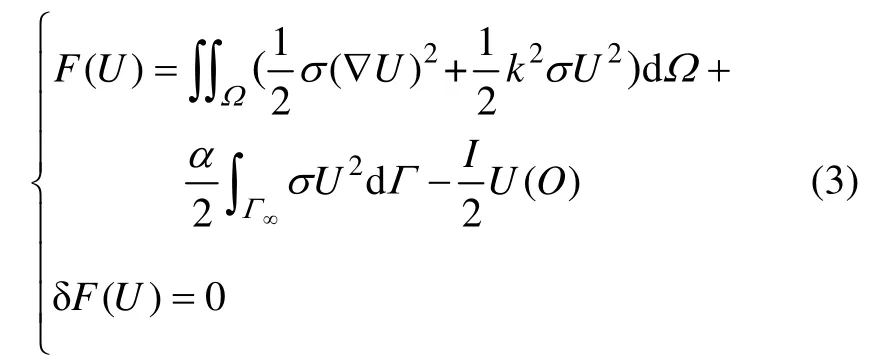
1.2 电阻率法有限元逼近

1.2.1 分块等级网格剖分

直流电阻率法正演实际上为求解具有点源奇点的椭圆边值问题。陈传淼[25]认为解决奇点问题最好的办法是局部加密网格法。

考虑半圆型求解区域Ω={(r,θ)|0＜ r＜1,0＜ θ＜π}。 首先，将Ω分为k个子扇形Ωi(i=1,2, …, k)，确保每个子扇形的圆心角αi＜π/2。然后，在每个子扇形上，以r 方向的剖分为基准，进行局部加密的三角形剖分。

设先将半径方向作均匀剖分 rk*=kh0(k=0, 1, …,N)，步长 h0=r∞/N。为了在O 点附近局部加密，可取区间J=[0, rl*]，并在其上取m 个等级网格节点。

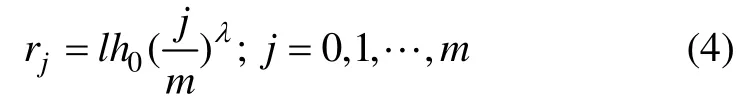
其中：等级网格参数λ ＞1。显然，rm=rl*=lh0。而小区间Ij=(rj,rj+1)的长度为

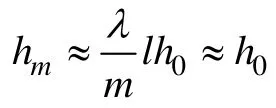
重新排列剖分节点为{r0, r1, …, rm=rl*, …,rm+N-l=rN*}，并对扇形Ωi进行局部加密的三角剖分。将半径为rj的圆弧作j 等分得到j+1 个节点，并将它们连接为折线。然后，用直线依次连接相邻两圆弧上的节点，得到1 个三角形网格。几个子区域上的网格就构成了所需的分块局部加密等级网格，见图2。为了简便，本文实际计算中直接取l=N，即在整个求解区域采取λ-等级网格。

1.2.2 单元分析

在单元e(逆时针编号依次为i, j, m)上进行三角形线性插值：

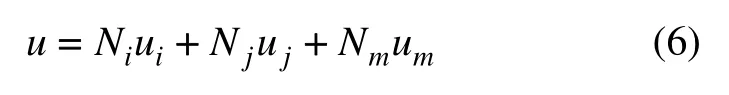
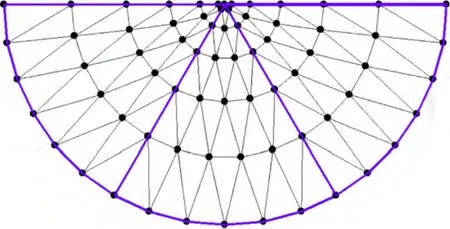
图2 λ=2 时的分块局部加密等级网格Fig.2 Piecewise locally refined graded mesh when λ=2

其中：

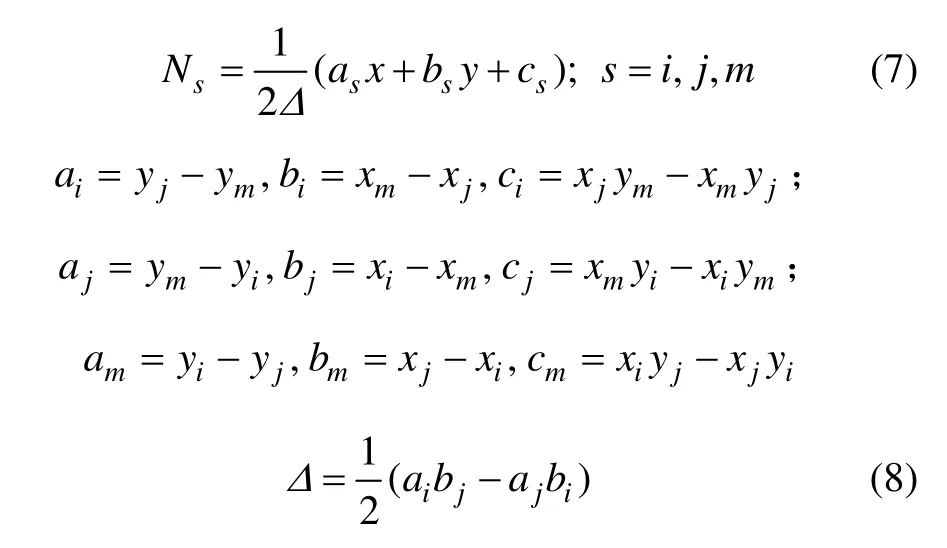
首先将式(3)中的积分分解成各单元e 上的积分。若单元e 内电导率为常数 σe，利用式(6)可得

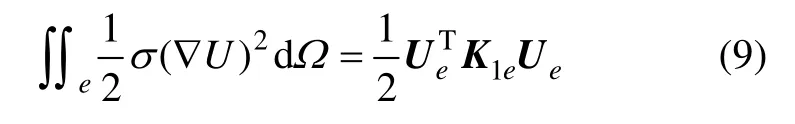
其中：Ue=(ui, uj, um)T，为单元e 的u 值列向量；K1e=(kst)3×3为3 阶对称矩阵；

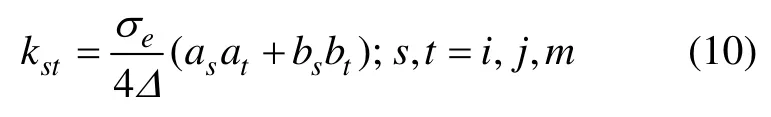
类似地，可得积分项

其中：

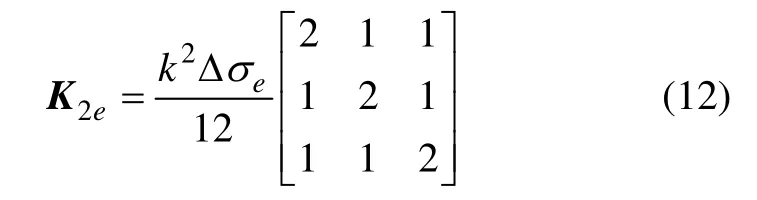
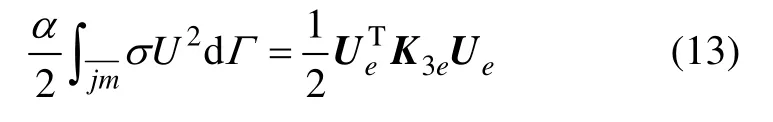
其中：

1.2.3 总刚合成

设区域Ω 剖分为n 个节点，将矩阵K1e，K2e和K3e相加可得3 阶单元刚度矩阵Ke，并扩展成n 阶方阵，然后叠加得

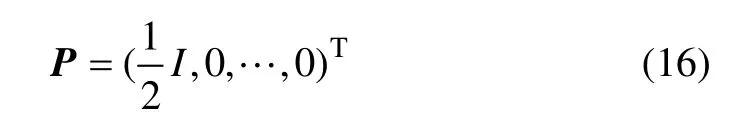
只有电源点对应位置非零(坐标原点为第1 个网格节点)；U 为未知的电位向量。

令式(15)变分为0，得到线性方程组

由式(10)，(12)及(14)知总体刚度矩阵K 为高度稀疏的对称正定矩阵，可利用PARDISO 等直接稀疏求解器快速求解得到波数域电位 U (x , y , k)。得到波数域中对应一系列不同波数ki时的电位 U (x , y , ki)后，利用Fourier 逆变换即可得到感兴趣的过点电源剖面(z=0)上的总电位：

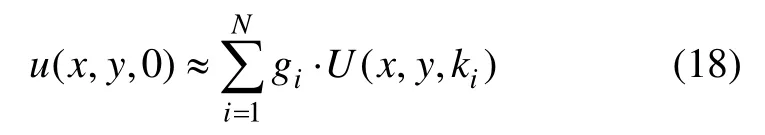
其中：ki和gi分别为离散波数及相应的权系数。采用文献[32]中由差分进化算法[33]计算得到离散波数，见表1。利用单源电场的电位，通过组合不同的采集装置，即可得到不同装置对应的视电阻率曲线，以用于电法勘探解释。

与通常采取的矩形计算区域相比，本文选取半圆型截断边界，简化了原问题(1)中截断边界上的混合边界条件，使得贝塞尔函数不必代入式(13)的边界积分进行计算，而只需计算 K0(kr∞)和 K1(kr∞)各1 次，大大简化了刚度矩阵的计算过程。另一方面，半圆形求解区域非常适合如图2 所示的结构化分块等级网格剖分，且能自动对奇点(点电源)局部加密，在保证精度的同时提高计算速度。若对矩形区域采取通常的结构化局部加密策略，即x 方向和y 方向分别采取由密到疏的剖分(如对数均匀或λ-等级网格)，则会出现如图3 所示非常扁长的矩形单元，网格质量下降，严重影响有限元模拟精度[25]。

图3 矩形域上局部加密网格Fig.3 Locally refined mesh on rectangular domain

1.3 压缩存储格式及总刚直接集成

1.3.1 行索引存贮格式(CSR)

此种存储格式按照行的顺序，依次将对称稀疏矩阵的上三角非零元素存放在一段连续存储空间上。假设A 为n 阶对称方阵，m 表示其上三角部分非零元的个数，数组下标从1 开始，则这种存储结构由以下3个数组构成：

双精度数组a，即按行存储A 的上三角部分的非零元素，长度为m；

整型数组Ja，即依次存储A 中元素的列号，长度为m；

整型数组Ia，即存储A 每行第1 个非零元在数组a 中的位置，长度为n+1。其中，Ia(n+1)=m+1，即第i行非零元个数为Ia(i+1)-Ia(i)。

图4 所示为1 个对称CSR 格式存储的示例。此种存储格式可用于Intel MKL的PARDISO直接稀疏求解器，并且存储效率非常高。对图3 所示的矩形网格采用矩形双线性元，有限元离散形成的总体刚度阵每行最多5 个非零元。而对图2 所示的等级网格，采用三角形线性元，总体刚度阵每行最多4 个非零元。

1.3.2 CSR 格式总刚直接集成

表1 离散波数及相应的权系数Table 1 Discrete wavenumbers and corresponding weights

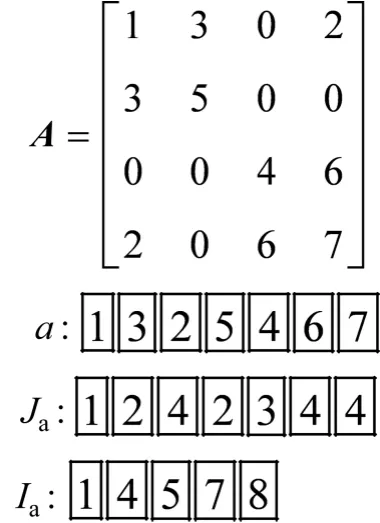
图4 CSR 格式存储示例Fig.4 Example of CSR storage format

分析刚度矩阵的组装过程得知：只有2 个节点相互关联(出现在同一单元中)，才会对总体刚度矩阵有贡献。在总刚K 的第i 行，非零元的列标正好为与节点i 关联的节点编号。为此，为每个节点i 设计1 个名为“关联节点”的数据结构，用于存储非零元的列标。

整数Ni，为与节点i 关联的节点个数；

整型数组Ci，为按升序依次存储关联节点编号。

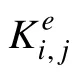
其中：

图5 关联节点示意图Fig.5 Schematic diagram of associated node

2 数值计算结果与分析

本文程序在Windows 7(Intel® CoreTMi5-760，2.8 GHz，4.0 GB 内存)下运行，软件平台为Intel Parallel Studio XE 2011，包含Intel Visual Fortran Compiler XE 12.0 以及Intel Math Kernel Library 10.3。

首先考虑扇形区域Ω={0＜ r ＜1,0＜ θ＜π/3}上如下拉普拉斯方程边值问题：

其中：边界函数g 由精确解u=r1/2sin(θ /2)确定，精确解在原点处不可导，具有奇性。采用如前所述的局部加密的等级网格，利用有限元方法求解椭圆边值问题(21)，计算结果如表2 所示(其中：N 为径向剖分数；误差表示数值解与精确解之间的最大绝对误差)。从表2 可看出，均匀网格下对此类奇异解问题，有限元只有半阶收敛；网格参数λ 增加1，收敛阶增加半阶；固定N，随着λ 增加，精度显著提高；λ 取4 时已达到线性有限元最高阶即2 阶收敛，故没必要进一步增大λ。另外，此例说明对此类奇异解问题，均匀剖分收敛非常缓慢，而采用局部加密的等级网格可显著提高有限元解的精度，即使λ=2 时128 等级剖分的计算精度(4.69×10-6)已与均匀1 024 剖分时的精度(4.20×10-6)相当，而λ=4 时128 等级剖分的误差仅为2.45×10-7，也远比均匀1 024 剖分时的4.20×10-6小；同时也验证了本文方法的可行性和有限元程序的正确性。

表2 等级网格有限元解收敛性分析Table 2 Convergence analysis of finite element solutions for graded meshes

需要指出的是：以上模型问题为调和方程边值问题，没有考虑物性的不均匀性以及附加源的影响；同时，精确解的奇性也比较弱，只在原点导数不存在，而函数仍是连续的。然而，在直流电法数值模拟中，地下存在复杂的电性不均匀结构，电性差异甚至可达几个数量级；同时电法正演问题为无界问题，需要进行截断边界处理，且在点电源处电位函数本身就不连续，为无穷大。这些都将导致有限元模拟精度及效率下降，因此，不能期望其达到如表2 所示模型问题的计算精度。

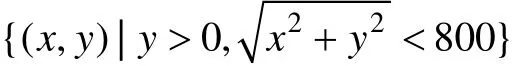
基于行索引稀疏存储模式，利用Intel MKL 的PARDISO 直接稀疏求解器求解有限元方程(17)。因为基于Cholesky分解的直接求解器计算时间主要取决于问题的规模及系数矩阵的稀疏结构，故每次求解962 001 阶有限元方程的时间差不多，约为4.5 s；而进行1 次完整的正演计算(需要解5 次方程组)，总耗时约为24.5 s，由此可知正演程序其它部分(包括5 次单元刚度阵的计算及总体刚度矩阵的集成) 仅耗时2 s。这是因为局部加密的λ-等级网格为结构化网格，生成的刚度矩阵稀疏结构简单，且每行最多7 个非零元，实际上考虑到对称性仅需存储4 个元素，不仅减小计算机内存，而且可大大简化总体刚度矩阵的集成。而采取半圆形求解区域，简化了原边值问题(1)截断边界Γ∞上的混合边界条件，使得贝塞尔函数不必参与单刚的计算，提高了总刚的计算速度。

2.1 模型一[28]

2 层水平地层：第1 层电阻率为10 Ω·m，厚度为10 m；第2 层电阻率为100 Ω·m。采用单极供电，供电电极位于坐标原点。图6 所示为两极装置得到的视电阻率曲线，其中精确解为线性滤波法计算结果[34]。图7 所示为主剖面上的相对误差分布。从图7 可看出：相对误差关于y 轴对称，且在y=10 左右有明显突变，反映出介质水平分界面的位置。

图6 两层地电模型计算结果Fig.6 Numerical results for two-layer geoelectric model

图7 主剖面上的相对误差Fig.7 Relative errors on main cross-section

从图6 可以看出：3 种不同的网格剖分，在远离电源点时(r＞3)都能够得到非常精确的结果，相对误差控制在0.5%以内；径向采取均匀剖分时(λ=1)，数值解在点源附近的误差较大，超过4%；局部加密等级网格在不增加计算工作量的前提下，显著提高了奇点附近的精度，且2 种不同的等级网格(λ=2, 3)得到几乎完全相同的结果。经计算，基于等级网格有限元解最大相对误差为 0.65%，而平均相对误差仅为0.30%。从计算时间和模拟精度2 个方面考虑，此例计算结果都与文献[28]中采用1 600×1 600(2 563 201个节点，2 560 000 个单元)均匀矩形剖分时，外推瀑布式多网格法的计算结果相当。文献[28]中计算时间为28 s，最大相对误差0.87%，平均相对误差0.22%。

2.2 模型二[5]

K 型3 层层状地层：第1 层电阻率为50 Ω·m，厚度为5 m；第2 层电阻率为100 Ω·m，厚度为10 m；第3 层电阻率为20 Ω·m。数值模拟结果见图8。从图8 可看出：采用等级网格的有限元法能在200 m 范围内得到高精度的计算结果，平均相对误差为0.29%；而200 m 以外相对误差显著增加，这是因为Fourier离散波数是基于均匀地层精确解利用200 m 内的极距序列最优化选取的，适用范围为1～200 m[29]。除此之外，可得到与模型一完全类似的结论：(1) 局部加密等级网格可显著提高奇点附近的模拟精度(x=1 附近相对误差从4.60%显著减为0.10%；(2) 网格参数λ=2和λ=3 对应的视电阻率误差曲线几乎重合，即对此类电法正演问题网格参数λ 取为2 即可。

2.3 模型三[21]

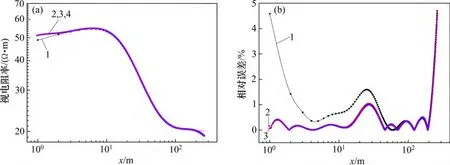
图8 3 层地电模型计算结果Fig.8 Numerical results for three-layer geoelectric model

图9 垂直电性界面模型计算结果Fig.9 Numerical results of vertical electrical interface

2D 垂直典型界面，左边介质电阻率为1 Ω·m，右边介质电阻率为100 Ω·m；单位点电源位于左边介质上，距界面5 m。基于局部加密等级网格的有限元法得到的视电阻率及相对误差如图9 所示，其中图9(b)中虚线表示分界面的位置。从图9 可看出：采用均匀网格剖分，奇点及分界面附近的相对误差比较大；而等级网格相对误差在1～200 m 范围内都比较小，控制在0.70%以内，与文献[21]中基于非结构化网格的自适应有限元计算结果精度相当，文献[21]中给出的误差限为0.69%。在介质分界面处(x=5 m)，这2 种网格剖分下视电阻率的相对误差均有体现，具有明显的突变。值得注意的是：利用等级网格，x=1 处的相对误差从3.94%骤降到0.12%，这进一步说明了等级网格的确能显著提高奇点附近的精度。

3 结论

(1) 在无穷远处截取圆形边界，大大简化了2.5D直流电法模拟电位满足的椭圆边值问题及单元刚度矩阵的计算。

(2) 局部加密等级网格能在不改变问题规模的前提下，显著提高2.5D 直流电法正演的有限元模拟精度。

(3) 对简单的模型问题，随着等级网格参数λ的增大(小于4)，奇异解的计算精度显著增大，但对直流电法正演影响不大，取为2 即可。

(4) 局部加密等级网格为结构化网格，避开了通常非结构化网格计算时繁琐的网格剖分及总刚集成过程，有限元程序实现简便。

(5) Intel MKL 的PARDISO 为一种高效、并行直接稀疏求解器，能在普通PC 机上5 s 内求解直流电阻率法正演有限元离散得到的100 万阶稀疏线性方程组，可用于各种地球物理正演问题的计算。

[1] Coggon J H. Electromagnetic and electrical modeling by the finite element method[J]. Geophysics, 1971, 36(1): 132-145.

[2] Dey A, Morrison H F. Resistivity modeling for arbitrarily shaped two dimensional structures[J]. Geophysical Prospecting, 1979,27(1): 106-136.

[3] 底青云, 王妙月. 稳定电流场有限元法模拟研究[J]. 地球物理学报, 1998, 41(2): 252-260.DI Qingyun, WANG Miaoyue. The real-like 2D FEM modeling research on the field characteristics of direct electric current field[J]. Chinese Journal of Geophysics, 1998, 41(2): 252-260.

[4] LI Changwei, XIONG Bin, QIANG Jianke, et al. Multiple linear system techniques for 3D finite element method modeling of direct current resistivity[J]. Journal of Central South University,2012, 19(2): 424-432.

[5] 李长伟, 阮百尧, 吕玉增, 等. 点源场井-地电位测量三维有限元模拟[J]. 地球物理学报, 2010, 53(3): 729-736.LI Changwei, RUAN Baiyao, LÜ Yuzeng, et al. Threedimensional FEM modeling of point source borehole-ground electrical potential measurements[J]. Chinese Journal of Geophysics, 2010, 53(3): 729-736.

[6] Li Y G, Spitzer K. Three-dimensional DC resistivity forward modelling using finite elements in comparison with finite-difference solutions[J]. Geophysical Journal International,2002, 151(31): 924-934.

[7] 罗延钟, 孟永良. 关于用有限单元法对二维构造作电阻率法模拟的几个问题[J]. 地球物理学报, 1986, 29(6): 613-621.LUO Yanzhong, MENG Yongliang. Some problems on resistivity modeling for two-dimensional structures by the finite element method[J]. Chinese Journal of Geophysics, 1986, 29(6):613-621.

[8] Mundry E. Geoelectrical model calculations for two-dimensional resistivity distributions[J]. Geophysical Prospecting, 1984, 32(1):124-131.

[9] 强建科, 罗延钟. 三维地形直流电阻率有限元法模拟[J]. 地球物理学报, 2007, 50(5): 1606-1613.QIANG Jianke, LUO Yanzhong. The resistivity FEM numerical modeling on 32D undulating topography[J]. Chinese Journal of Geophysics, 2007, 50(5): 1606-1613.

[10] 阮百尧, 徐世浙. 电导率分块线性变化二维地电断面电阻率测深有限元数值模拟[J]. 地球科学: 中国地质大学学报, 1998,23(3): 303-307.RUAN Baiyao, XU Shizhe. FEM for modeling resistivity sounding on 2D geoelectric model with line variation of conductivity within each block[J]. Earth Science: Journal of China University of Geoscience, 1998, 23(3): 303-307.

[11] 阮百尧, 熊彬. 电导率连续变化的三维护电阻率测深有限元模拟[J]. 地球物理学报, 2002, 45(1): 131-138.RUAN Baiyao, XIONG Bin. A finite element modeling of three-dimensional resistivity sounding with continuous conductivity[J]. Chinese Journal of Geophysics, 2002, 45(1):131-138.

[12] TANG Jingtian, WANG Feiyan, XIAO Xiao, et al. 2.5D DC resistivity modeling considering flexibility and accuracy[J].Journal of Earth Science, 2011, 22(1): 124-130.

[13] WU Xiaoping. A 3D finite-element algorithm for DC resistivity modeling using shifted incomplete cholesky conjugate gradient method[J]. Geophysical Journal International, 2003, 154(3):947-956.

[14] 吴小平, 汪彤彤. 利用共轭梯度算法的电阻率三维有限元正演[J]. 地球物理学报, 2003, 46(3): 428-432.WU Xiaoping, WANG Tongtong. A 3D finite-element resistivity forward modeling using conjugate gradient algorithm[J].Chinese Journal of Geophysics, 2003, 46(3): 428-432.

[15] 熊彬, 阮百尧. 电位双二次变化二维地电断面电阻率测深有限元数值模拟[J]. 地球物理学报, 2002, 45(2): 285-295.XIONG Bin, RUAN Baiyao. A numerical simulation of 2D geoelectric section with biquadratic change of potential for resistivity sounding by the finite element method[J]. Chinese Journal of Geophysics, 2002, 45(2): 285-295.

[16] 徐世浙. 地球物理中的有限单元法[M]. 北京: 科学出版社,1994: 131-205.XU Shizhe. The finite element method in geophysics[M].Beijing: Science Press, 1994: 131-205.

[17] 徐世浙, 刘斌, 阮百尧. 电阻率法中求解异常电位的有限单元法[J]. 地球物理学报, 1994, 37(S2): 511-515.XU Shizhe, LIU Bin, RUAN Baiyao. The finite element method for solving anomalous potential for resistivity surveys[J].Chinese Journal of Geophysics, 1994, 37(S2): 511-515.

[18] Zhou B, Greenhalgh S A. Finite element three-dimensional direct current resistivity modeling: Accuracy and efficiency considerations[J]. Geophysical Journal International, 2001, 145:679-688.

[19] 汤井田, 公劲喆. 三维直流电阻率有限元-无限元耦合数值模拟[J]. 地球物理学报, 2010, 53(3): 717-728.TANG Jingtian, GONG Jinzhe. 3D DC resistivity forward modeling by finite-infinite element coupling method[J]. Chinese Journal of Geophysics, 2010, 53(3): 717-728.

[20] 陈小斌, 胡文宝. 有限元直接迭代算法及其在线源频率域电磁响应计算中的应用[J]. 地球物理学报, 2002, 45(1): 119-130.CHEN Xiaobin, HU Wenbao. Direct iterative finite element(DIFE) algorithm and its application to electromagnetic response modeling of line current source[J]. Chinese Journal of Geophysics, 2002, 45(1): 119-130.

[21] 汤井田, 王飞燕, 任政勇. 基于非结构化网格的2.5D 直流电阻率自适应有限元数值模拟[J]. 地球物理学报, 2010, 53(3):708-716.TANG Jingtian, WANG Feiyan, REN Zhengyong. 2.5D DC resistivity modeling by adaptive finite-element method with unstructured triangulation[J]. Chinese Journal of Geophysics,2010, 53(3): 708-716.

[22] 任政勇, 汤井田. 基于局部加密非结构化网格的三维电阻率法有限元数值模拟[J]. 地球物理学报, 2009, 52(10):2627-2634.REN Zhengyong, TANG Jingtian. Finite element modeling of 3D DC resistivity using locally refined unstructured meshes[J].Chinese Journal of Geophysics, 2009, 52(10): 2627-2634.

[23] REN Zhengyong, TANG Jingtian. 3D direct current resistivity modeling with unstructured mesh by adaptive finite-element method[J]. Geophysics, 2010, 75(1): 7-17.

[24] TANG Jingtian, REN Zhengyong, WANG Feiyan, et al. 3D direct current resistivity forward modeling by adaptive multigrid finite element method[J]. Journal of Central South University of Technology, 2010, 17(3): 587-592.

[25] 陈传淼. 科学计算概论[M]. 北京: 科学出版社, 2007:120-262.CHEN Chuanmiao. Introduction to scientific computing[M].Beijing: Science Press, 2007: 120–262.

[26] Moucha R, Bailey R C. An accurate and robust multigrid algorithm for 2D forward resistivity modelling[J]. Geophysical Prospecting, 2004, 52(3): 197-212.

[27] 鲁晶津, 吴小平, Spitzer K. 直流电阻率三维正演的代数多重网格方法[J]. 地球物理学报, 2010, 53(3): 700-707.LU Jingjin, WU Xiaoping, Spitzer K. Algebraic multigrid method for 3D DC resistivity modeling[J]. Chinese Journal of Geophysics, 2010, 53(3): 700-707.

[28] 潘克家, 汤井田, 胡宏伶, 等. 直流电阻率法2.5D 正演的外推瀑布式多重网格法[J]. 地球物理学报, 2012, 55(8):2769-2778.PAN Kejia, TANG Jingtian, HU Hongling, et al. Extrapolation cascadic multigrid method for 2.5D direct current resistivity modeling[J]. Chinese Journal of Geophysics, 2012, 55(8):2769-2778.

[29] PAN Kejia, TANG Jingtian. 2.5D and 3D DC resistivity modelling using an extrapolation cascadic multigrid method[J].Geophysical Journal International, 2014, 197(3): 1459-1470.

[30] LI Changwei, XIONG Bin, QIANG Jianke, et al. Multiple linear system techniques for 3D finite element method modeling of direct current resistivity[J]. Journal of Central South University,2012, 19(2): 424-432.

[31] Wang W, Wu X, Spitzer K. Three-dimensional DC anisotropic resistivity modelling using finite elements on unstructured grids[J]. Geophysical Journal International, 2013, 193(2):734-746.

[32] 潘克家, 汤井田. 2.5D 直流电法正演中Fourier 逆变换离散波数的最优化选取[J]. 中南大学学报(自然科学版), 2013, 44(7):2819-2826.PAN Kejia, TANG Jingtian. Optimized selection of discrete wavenumbers for inverse Fourier transform in 2.5D DC resistivity modeling[J]. Journal of Central South University(Science and Technology), 2013, 44(7): 2819-2826.

[33] 潘克家, 陈华, 谭永基. 基于差分进化算法的核磁共振T2谱多指数反演[J]. 物理学报, 2008, 57(9): 5956-5961.PAN Kejia, CHEN Hua, TAN Yongji. Multi-exponential inversion of T2spectrum in NMR based on differential evolution algorithm[J]. Acta Physica Sinica, 2008, 57(9): 5956-5961.

[34] Guptasarma D, Singh B. New digital linear filters for Hankel J0and J1transforms[J]. Geophysical Prospecting, 1997, 45(5):745-762.