基于改进标记传播算法的基因表达谱数据分析

王年，葛芳，王俊生，唐俊

(安徽大学 计算智能与信号处理教育部重点实验室，安徽 合肥，230039)

DNA 微阵列技术为肿瘤学提供了一种全新的研究手段，1 次基因芯片实验可以获得成千上万个基因的信息。随着DNA 微阵列技术的进步和仪器设备的更新，基因表达谱数据将不断积累，这类数据的主要特点是样本少、维数高、冗余基因和噪声多，因此，如何对这类“新型”数据进行分析，挖掘其中包含的有效信息，已成为生物信息学研究的重点问题之一[1-3]。传统的基因表达谱分析方法主要是对基因数据进行信息基因选取或特征属性提取后，再用相应的分类或聚类方法对样本进行识别[4-6]，其中聚类是一种无监督学习方法。传统的聚类方法，如模糊C 均值[7]和自组织映射[8]等，均要求数据呈球状分布，且这类算法易陷入局部最优。近年来，半监督聚类方法成为机器学习领域的研究热点。Zhu 等[9]用高斯随机场的方法处理半监督学习问题，提出了标记传播算法，并根据随机游走对标记传播算法进行了概率解释。Wang等[10-11]基于任意数据点的类标号可以由其近邻点的类标号进行线性重构的假设，提出了基于线性近邻的标记传播算法；Bai 等[12]将标记传播进行了扩展，提出了基于上下文分析的图传导算法，并将其应用于图像分割、形状检索和匹配等领域。标记传播是一种基于图的半监督聚类方法，该方法利用少量已标记类别的样本，通过传播标记的方式来识别未知类别的样本，能在任意形状的样本空间中进行聚类，克服了传统聚类方法易陷入局部最优的缺点。然而，原始标记传播算法迭代次数过大，每次迭代前都要重新标记已知类别的样本，且最终的划分准则也并不明确。针对上述问题，结合Gauss-Seidel 迭代[13]算法的思想，本文提出一种改进的标记传播算法，并将其应用于基因表达谱数据分析。通过对白血病和结肠癌数据集的实验，证明本文方法的有效性。

1 基因表达谱数据的权值矩阵表示

设{ g1, g2, …, gm}表示一个样本中所有基因构成的集合，其中 gj(1≤ j ≤ m)表示1 个基因，m 表示基因个数；设{ x1, x2, …, xn}表示由所有实验样本构成的集合，其中 xi(1≤ i ≤ n)表示在同一条件下所有基因的表达值，n 表示样本个数。由所有样本构成的基因表达谱矩阵M 可表示为

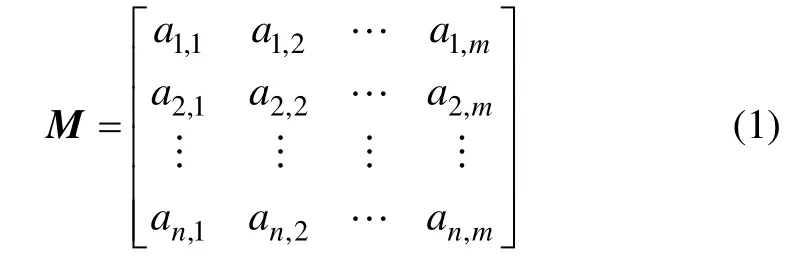
其中：aij为基因gj在样本xi中的表达值。

根据谱图理论，以样本为节点构造赋权图G(V,E)(其中：V 为待聚类的样本集；E=V×V 表示边集)。设节点xi和xj之间的边权值为Wij，本文所选择的相似性度量为

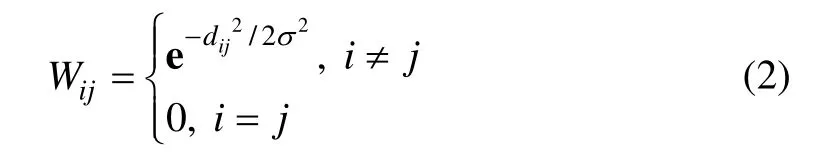
其中： i ,j=1,2, … ,n；dij表示节点xi和xj之间的欧氏距离；σ 为权重参数，通常，σ 可以根据节点xi和xj的K 个近邻的平均距离来自适应调整[14]，K 是一个经验值。显然，对于任意的xi，xj和σ ，有0≤Wij≤1，反映了节点xi和xj之间的亲近程度，Wij越大，则节点xi和xj越有可能属于同一类。另外，定义如下Laplace 矩阵：

其中：D 为度对角矩阵，且有 Dii=∑kWik。

2 标记传播算法

标记传播算法将某些样本标记为已知，并将样本集划分为已标记样本{ x1, x2, …, xl}和未标记样本{xl+1,xl+2, …,xl+u}，其中，l + u=n，且满足l＜＜ u。令YL=(y1, y2, …, yl)表示已知样本的标记，同时定义一个标记序列f=[fLfU]T表示最终的标记结果，其中， fL=YL。标记传播的步骤如下。

Step 1: 传播标记，f←D-1Wf ；

Step 2: 强化标记数据， fL=YL；

Step 3: 返回Step 1，直到f 收敛。

通过step 1，将已标记样本节点的标记传播至相邻的节点；同时，在标记传播的过程中，已知样本的标记是保持不变的，以保证标记数据的强度，指导标记传播过程的正确性；算法迭代终止后，标记序列f包含了样本的类别信息。Zhu[9]给出了标记传播算法的收敛解：

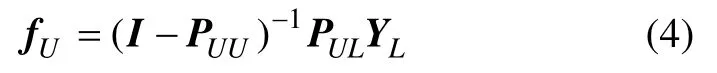
其中：PUU和PUL是迭代矩阵P=D-1W 的子矩阵块，即

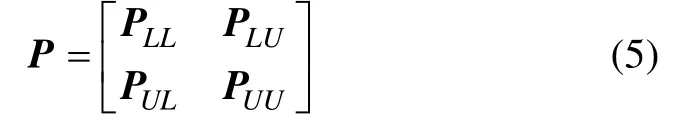
因此，标记传播算法的解将收敛于1 个固定解。需要指出的是，根据式(5)可以直接求出未知样本的标记。

3 改进的标记传播算法

通过上述方法任意数据点xi都可以映射为相应的实数值fi，但该算法在每次迭代前都要重新标记已知样本，且由于标记传播过程和标记强化过程分离，造成算法迭代次数过大；同时，该算法采用0-1 标记，需要选取适合的阈值对样本进行分类。Zhu 等[9]使用的0.5 阈值缺乏稳定性，应用于复杂数据时并不能取得很好的效果。

3.1 基于Gauss-Seidel 迭代的标记传播算法

设线性方程组Ax=b，矩阵A 为实对称矩阵，且满足A=D - W1-W2。其中：D 为对角矩阵；W1为下三角矩阵；W2为上三角矩阵。若迭代矩阵J=(D -W1)-1W2的谱半径 ρ(J)＜1，则可以利用Gauss-Seidel迭代求解该方程组，如在第t+1次迭代后，该方程组的近似解为

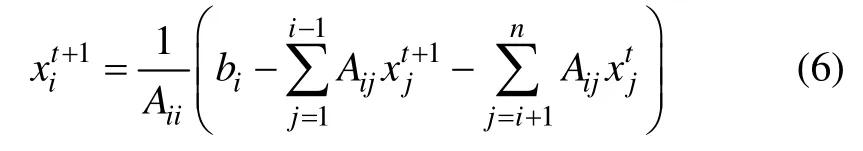
令 x=f ,b=f0，其中： f0=(y1, …, yl,0, … ,0)，同时令A=IL+μL，μ∈(0,1)为可调参数，IL为对角矩阵，且满足

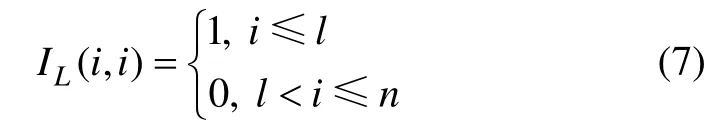
根据Gauss-Seidel 迭代算法，经过t+1 次迭代后，数据点xi的标记为

由 于Aij=ILij+μ(Dij-Wij)=-μWij， 同 时 有Aii=ILii+μ(Dii-Wii)=ILii+μ Dii，因此，

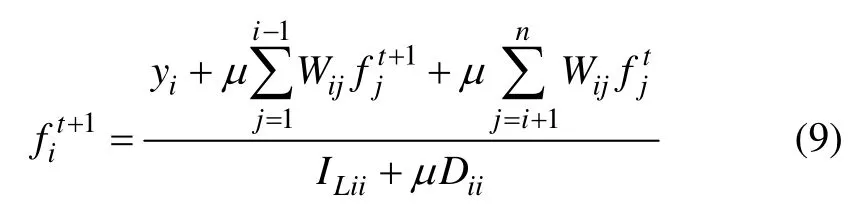
由式(9)可知：在每次迭代过程中，数据点从初始标记节点中获取一部分标记信息；同时，由于相似节点间的权重较大，使得数据点可以从其近邻点中获取一部分标记信息，当传播终止后，相似节点的分布情况也趋于一致。化简式(9)可得

式(10)可以改写为

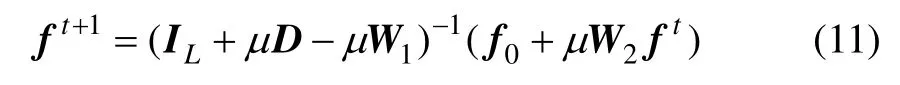
利用式(11)更新每个数据点的标记，直到收敛。这里，对初始标记点使用正负标记的方式，如对于两类问题，将其中一类的若干个样本标记为1，而另一类的若干个样本标记为-1。对于最终的收敛结果，能以零为分割点对未知类别的样本进行划分。

3.2 收敛性证明

本节将证明标记序列f 的收敛性，展开式(11)可得

令Q=(IL+μD -μW1)-1μW2，显然Qij≥ 0且∑jQij＜1。根据Perron-Frobenius 定理[13]，Q 的谱半径小于1；同时，由于0＜μ＜1，且0＜Wij＜1，因此，

其中：E 为单位矩阵。因此， ft将最终收敛于

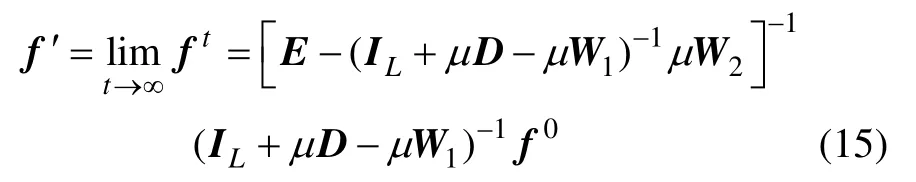
化简式(15)，可得

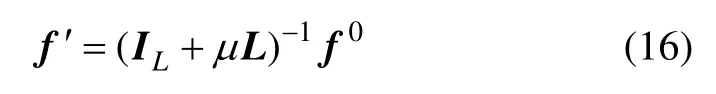
因此，本文算法的解是收敛的。同样，可以通过式(16)直接求出所有样本的最终标记值。

4 实验结果与分析

4.1 实验数据

选用 2 组公开的癌症数据集：白血病数据(leukemia)，共52 个样本，其中24 个样本为急性淋巴白血病(ALL)，28 个样本为急性粒细胞白血病(AML)，每个样本含有12 564 个基因表达数据(数据源于http://www.broad.mit.edu/cgi-bin/cancer/datasets.cgi) ；结肠癌数据(colon cancer)，共62 个样本，其中22 个样本被确定为正常样本，40 个被确定为肿瘤样本，每个样本含有 2 000 个基因表达数据(数据源于http://linus.nci.nih.gov/～brb/DataArchive_New.html)。本文实验是在酷睿双核主频2.60 GHz，内存为2 G 的计算机上运行的。

癌症基因表达谱数据的获取过程十分复杂，所得到的数据含有大量的噪声，同时每个样本都记录了组织细胞中所有可测基因的表达水平，但只有较少数基因包含与类别相关的信息，因此，对数据进行预处理是必要的，定义下式对基因表达谱数据进行筛选：

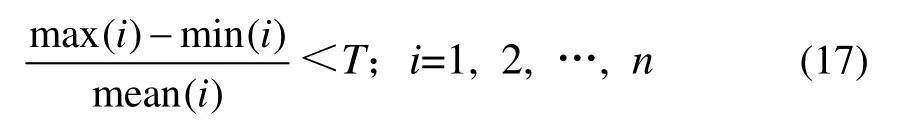
其中：max(i)表示为第i 个基因在所有样本中表达水平的最大值；min(i)表示为第i 个基因在所有样本中表达水平的最小值；mean(i)表示为第i 个基因在所有样本中表达水平的平均值；T 为给定的阈值。若某个基因的表达情况符合式(17)，则将该基因剔除。

4.2 白血病数据实验

将白血病数据的第1 号样本(ALL)标记为1，第25 和52 号样本(AML)标记为-1，分别进行t=5，10，50，100 次迭代，更新每个样本点的标记，观察标记序列各分量的变化，结果如图1 所示。

图1 中，标记序列的前24 个分量对应的是白血病数据集的ALL 样本，后28 个分量对应AML 样本。由图1 可知：当进行5 次迭代后，ALL 样本的标记均大于0，而AML 样本的标记均小于0，所有样本被正确地划分为2 类，证实本文方法可以快速且有效的实现样本类别的划分；随着迭代次数的增加，2 类样本标记值的区别更加明显，同时第1 号样本的标记值始终为1，而第25 和52 号样本的标记值始终为-1，这说明初始标记点的标记信息在每次迭代时都被保留下来；当进行50 次和100 迭代后，标记序列各分量的变化并不明显，说明经过较少次数的迭代就可以得到最终的收敛结果。

4.3 结肠癌数据实验

将结肠癌数据的第1 号样本(正常组织样本)标记为1，第62 号样本(肿瘤组织样本)标记为-1，同样分别进行t=5，20，100 和200 次迭代，结果如图2 所示。

图2 中，标记序列的前22 个分量对应的是结肠癌数据集的正常组织样本，后40 个分量对应肿瘤组织样本。由图2 可知：初始标记点的标记值在标记传播过程中始终保持不变。当经过5 次迭代后，2 类样本标记的区别并不明显，但经过20 次迭代后，就可以看出2 类样本的标记的差异性，在正常组织样本中，第18和20 号样本被错误标记，而在肿瘤组织样本中，第52，55 和58 号样本被错误标记，准确率达到91.94%，在实际情况中，这些样本中含有较多的偏离值和异常点，从而导致样本异常表达；同时，进行100 次和200次迭代后，样本标记值的变化已并不明显，这同样说明本文方法可以快速实现标记序列的收敛。

在理想情况下，初始标记点的选取是任意的，但在实际情况中，某些样本含有较多的噪声和异常表达值，若将其作为初始迭代点，则最终的迭代结果会受到一定的影响。因此，为了观察初始标记点对最终迭代结果的影响，分别将结肠癌数据中被错误标记的第20，52 和55 号样本标记为已知，结果如图3 所示。

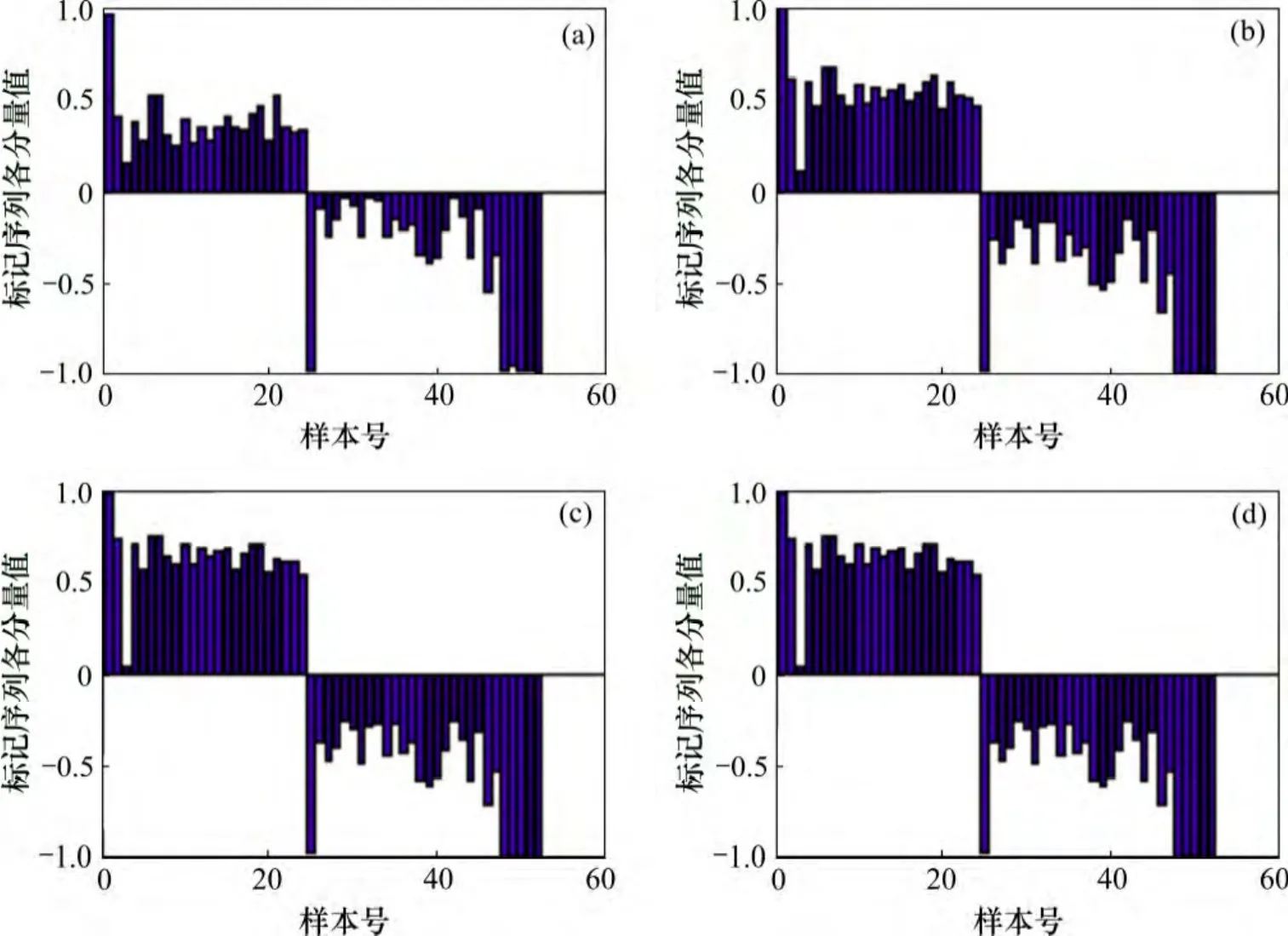
图1 白血病数据的标记传播过程Fig.1 Label propagation processes of leukemia data

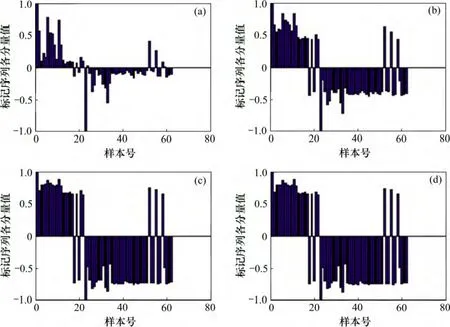
图2 结肠癌数据的标记传播过程Fig.2 Label propagation processes of colon cancer data

图3 异常样本被标记为已知的迭代结果Fig.3 Iterative results by labeling abnormal samples

图3(a)中仅标记了第1 和23 号样本；图3(b)中除标记第1 和23 号样本外，同时将第20 号样本标记为1；图3(c)和(d)除标记第1 和23 号样本外，分别将第52 号和55 号样本标记为-1。由图3(b)可知：当将第20 号样本标记为已知，除20 号样本外的正常组织样本的标记值并没有受到明显的影响，肿瘤组织样本中的第52，55 和58 号样本的标记值也基本没有变化，而其他样本标记值的绝对值减小却趋于减小，同时第24 和59 号样本被错误标记到另一类中。由图3(c)～(d)可知：当将第52 或55 号样本标记为已知时，第13至22 号样本全部被错误标记，同时第1 至12 号样本的标记值的绝对值也相应地减小，这主要是由于在标记传播过程中，某个样本的标记是根据其近邻样本点的标记进行更新的。因此，若将某个异常表达的样本标记为已知，则与该样本相似的正常表达样本，其标记值也会趋向于与该样本的相似，甚至会被错误标记。

4.4 对比验证

为了进一步验证本文方法的正确性，将本文方法与传统的S2N_KNN[1]法以及另外2 种基于图的方法即局部线性嵌入法(Locally Linear Embedding,LLE)[5,15]和归一化割法(Normalized Cut, Ncut)[16]进行对比。S2N_KNN 以“信噪比”为指标选取特征基因，再用K-近邻(KNN)分类器对样本进行分类；LLE 是一种流行学习方法，本文先以LLE 提取样本特征，再结合KNN 实现样本的分类。Ncut 通过计算规范Laplace矩阵的次小特征值对应的特征向量(Fiedler 向量)来进行聚类，结果如表1 所示。

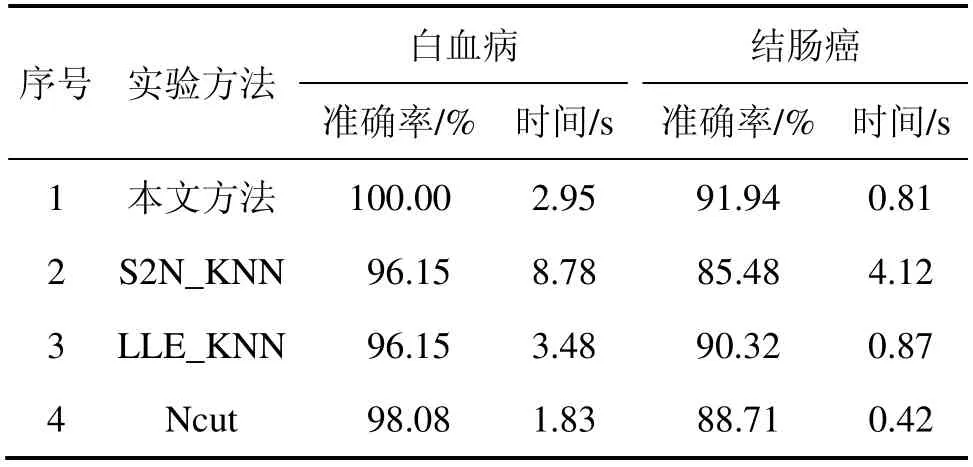
表1 本文方法与另外3 种方法的实验结果比较Table 1 Comparisons of experiment results with other three methods

由表1 可知：无论从准确率还是运算效率方面，本文方法都比传统的S2N_KNN 法的高。传统方法以降维来提取特征基因势必会丢失部分含有分类信息的基因，而本文方法将样本数据作为高维空间中的点，所构造的权值矩阵反映了样本之间的关系，使得原来的样本分类信息完全映射到低维的权值矩阵中。同时，本文方法首先以样本为节点构图，其低样本特性决定了构造的矩阵规模较小，从而具有较低的运算复杂度，有利于基因表达数据的快速聚类。

另外，从准确率方面，本文方法明显高于另外2种基于图的方法。LLE 算法是一种有效的可视化方法，但其要求数据服从流形分布，提取的特征并不具有很强的分类能力。Ncut 在聚类时倾向于所得到的类具有相同的类内相似度，且Fiedler 向量并不一定能够反映原始数据的结构；而本文方法通过在近邻点之间传播标记的方式来学习分类，并不会受到数据分布形状的限制。同时，在效率上，本文方法并不具有明显的优势，这是因为这几种方法都是利用构图的方法将高维样本映射到低维空间，构造的矩阵规模是相同的。

5 结论

(1) 针对原始标记传播算法存在的问题，结合Gauss-Seidel 迭代的思想，提出了一种改进的标记传播算法，并将其应用于基因表达谱数据分析。

(2) 通过2 组癌症数据集的实验，证明本文方法可以快速有效地实现基因表达谱数据的聚类。该方法克服了迭代次数过大和重复标记数据点的缺点；同时在数据类别划分时使用正负标记的方式，避免了采用0-1 标记时阈值选取的不确定性。

(3) 与传统标记传播算法一样，该方法的不足之处是初始标记点的选取对最终迭代结果具有一定的影响，这有待进一步研究与探讨。

[1] Singh D, Febbo P G, Ross K, et al. Gene expression correlates of clinical prostate cancer behavior[J]. Cancer Cell, 2002, 1(2):203-209.

[2] Dash S, Patra B. A study on gene selection and classification algorithms for classification of gene expression profile[J].International Journal of Research and Reviews in Computer Science, 2011, 2(5): 1212-1217.

[3] 沈威, 郑明, 刘桂霞, 等. 基于奇异值求通解方法进行基因调控网络构建[J]. 中南大学学报(自然科学版), 2012, 43(4):1377-1381.SHEN Wei, ZHENG Ming, LIU Guixia, et al. Construction of gene regulatory network based on singular value decomposition for solution set[J]. Journal of Central South University (Science and Technology), 2012, 43(4): 1377-1381.

[4] 李宏, 李翔, 吴敏, 等. 基于闭合模式的高维基因表达谱多类分类[J]. 中南大学学报(自然科学版), 2008, 39(5): 1035-1041.LI Hong, LI Xiang, WU Min, et al. Multi-class classification of high-dimension gene expression profile based on closed patterns[J]. Journal of Central South University (Science and Technology), 2008, 39(5): 1035-1041.

[5] LI Bo, ZHENG Chunhou, HYANG Deshuang, et al. Gene expression data classification using locally linear discriminant embedding[J]. Computers in Biology and Medicine, 2010,40(10): 802-810.

[6] Kancherla K, Mukkamala S. Feature selection for lung cancer detection using SVM based recursive feature elimination method[J]. Machine Learning and Data Mining in Bioinformatics, 2012, 7246: 168-176.

[7] Tari L, Baral C, Kim S. Fuzzy c-means clustering with prior biological knowledge[J]. Journal of Biomedical Informatics,2009, 42(1): 74-81.

[8] Patterson A D, LI Henghong, Eichler G S, et al.UPLC-ESI-TOFMS-based metabolomics and gene expression dynamics inspector self-organizing metabolomic maps as tools for understanding the cellular response to ionizing radiation[J].American Chemical Society, 2008, 80(3): 665-674.

[9] ZHU Xiaojin. Semi-supervised learning with graphs[D].Pennsylvania: Carnegie Mellon University. School of Computer Science, 2005: 5-8.

[10] WANG Fei, ZHANG Changshui. Label propagation through linear neighborhoods[J]. IEEE Transactions on Knowledge and Data Engineering, 2008, 20(1): 55-67.

[11] WANG Jingdong, WANG Fei, ZHANG Changshui, et al. Linear neighborhood propagation and its applications[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009,31(9): 1600-1615.

[12] BAI Xiang, YANG Xingwei, Latecki L J, et al. Learning context-sensitive shape similarity by graph transduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2010,32(5): 861-874.

[13] Saad Y. Iterative methods for sparse linear systems[M]. Boston:PWS Publishing Company, 1996: 104-107.

[14] Zelnik-Manor L, Perona P. Self-tuning spectral clustering[J].Advances in Neural Information Processing Systems, 2004,17(2): 1601-1608.

[15] Shi C, Chen L. Feature dimension reduction for microarray data analysis using locally linear embedding[C]// Proceeding of 3rd Asia-Pacific Bioinformatics Conference. London: Imperial College Press, 2005: 211-217.

[16] Dhillon I S, GUAN Yuqiang, Kulis B. Kernel k-means-spectral clustering and normalized cuts[C]// Proceedings of the Tenth ACM SIGKDD International Conference on Knowledge Discovery and Data Mining. New York: Association for Computing Machinery, 2004: 551-556.