生物芯片微阵列图像倾斜校正算法研究

吴灶全，陈熹，娄艳阳，陈杰，刘正春

(中南大学 地球科学与信息物理学院，生物医学工程研究所，湖南 长沙，410083)

生物芯片是通过平面微细加工技术在固体芯片表面构建的微流体分析单元和系统，以实现对细胞、蛋白质、核酸以及其他生物组分的准确、快速、大信息量的检测，具有多通道、高通量、并行自动处理等优点。通过处理和分析生物芯片数字荧光图像，识别并提取阵列中每个样点区域的信号强度，进行定量分析和相关信息挖掘[1-3]。样点的识别和分割是微阵列分析的核心，但是由于误差和外界干扰，在制备和扫描过程中芯片和图像经常会出现一定程度的倾斜和旋转，甚至样点分布歪曲。这样，芯片图像中样点阵列的准直特性必定受到影响，网格定位结果将会出现较大误差，最终导致样点的识别与分割不准确，也得不到满意的分析效果。常见的倾斜校正方法有霍夫(Hough)变换，傅里叶(Fourier)变换，拉东(Radon)变换，投影特性法和最小二乘法等[4-8]，根据它们改进的算法一直都是研究的重点。Meyenhofer 等[9]通过计算投影波形的方差寻找校正角度，并进行多次投影计算获得最大投影方差值，对应的角度即为图像倾斜角度。该方法在寻优的过程中需要多次对芯片图像进行投影计算以及方差计算，在同样精度下计算效率显得相当低。Deng 等[10]通过计算投影波形的能量谱密度获得旋转角度，并进行多次旋转搜索获得最大能量谱密度，对应的角度即为最佳校正角度。该方法尽管减少了校正角度的搜索次数，但是每次搜索都需要通过傅里叶变换计算能量谱密度，庞大的计算量约束了倾角检测的速度。刘艳等[11]运用Sobel 算子对芯片图像进行边界提取，然后通过Radon 变换确定倾斜角度。虽然边界提取能减少Radon 变换的计算量，但是在检测矩形样点图像的倾角时运算效率不高。严伟等[12]提出了Radon 变换和功率谱估计相结合的功率切片方法，并以此建立起三维功率谱密度图，实现倾斜角度的精确计算。该方法采取了Radon 投影和功率谱的级联运算，但检测精度仅为1.0°，且计算量也相当庞大。这些常见的倾斜校正算法一般都使用单一的方法处理各种形状样点的微阵列图像，造成对某些形状样点图像的倾斜校正效果不佳[13-14]。通过比较分析发现矩形样点和圆形样点在形状和几何空间规律上有明显的差别，综合考虑校正精度和运算速度等因素，本文作者提出了对矩形和圆形样点的芯片图像分别采用改进的Hough变换和改进的Radon 变换进行倾角检测。

1 倾斜校正算法

1.1 改进的Hough 变换

Hough 变换将xy 平面直线检测问题转化为ρθ 参数空间寻找局部最大值的问题，能有效地检测直线倾斜角度，并广泛应用于检测感兴趣的区域边缘。Hough变换的优点在于抗噪声的能力强，并不受图像中直线走势的影响。但Hough 变换的精确度和运算复杂度存在着矛盾，而且对存储空间的要求比较大[15-16]。ρθ 参数空间量化得越精细，算法的精度越高，算法所需的存储空间和运算量也越大。虽然生物芯片的倾斜角度不大，大量统计得到倾斜角度范围是[-5°，5°]，但是要求的精度比一般的直线检测要高[17]，为了适应生物芯片技术的发展，倾角的检测精度如能从0.1°提升到0.01°，有利于提高分析结果的精确度。本文结合了矩形样点的形状和分布特点对Hough 变换进行改进，从而提高样点边缘检测精度，减少ρθ 参数空间的计算量，提升其实用价值。

在对Hough 变换进行改进的过程中，参考了倾斜文档扫描图像的校正方法[18-19]。倾斜文档图像的校正方法中经常将文字简化成类似矩形的连通体，并通过提取水平边缘来减少计算量。针对矩形样点的形状特征和分布规律，本算法对Hough 变换进行了改进。对生物芯片图像进行二值化后，仅计算矩形样点的上下边缘像素的Hough 参数和累计值。根据所得的Hough参数空间，提取占主导的直线组，并计算出直线组平均倾斜角度，从而得到最佳校正角度。

1.1.1 对生物芯片图像进行二值化

本算法将采用大津算法(Otsu 算法)法对生物芯片图像进行二值化，它在确保运算速度与准确度的同时，能将样点与背景很好地分割开来[20-21]。Otsu 算法，又称最大类间方差法，是一种自动的非参数非监督的阈值选择法，具有优良的性能，其效果一直是分割算法中的参考标准[22-23]。当部分背景被错分为对象时，会导致两类之间的差别变小。而Otsu 法的原理正是选择阈值使得背景与对象两类之间的方差最大化，即两部分之间的差别最大，意味着错分的概率最小，类间分割效果最好。

在检测倾斜角度之前，先对生物芯片图像进行灰度化，然后进行一次形态学的开闭运算级联操作[24]。由于开操作能抑制较小的亮噪声，闭操作能抑制背景的暗噪声，因此开闭操作消除了图像中的孤立亮点，平滑背景并保留了样点主体区域。开闭操作会产生一定的模糊，为保证尽量小地改变样点形状，应该选择较小的结构元。接着选择Otsu 算法自动计算最佳分割阈值，并使用这阈值将芯片图像二值化。所得二值图像的白色区域(灰度为255)代表芯片样点，黑色区域(灰度为0)代表芯片背景，这样就消除了原图像背景中噪声的干扰，也减少一定的计算量。

1.1.2 计算Hough 参数空间

在运用Hough 变换进行倾斜检测时，若对图像中每一个像素点都进行Hough 变换，那么计算量相当大，将会影响算法运算速度，降低其实用价值。本算法提出在进行Hough 变换之前先对像素点进行判别，若当前像素点符合条件，则进行Hough 变换，否则跳转到下一个像素点。这不仅可以减少部分矩形样点的不平整边缘的影响，还大大提高了运算速度和准确度。

像素点的灰度判别准则：若当前像素灰度为0，且下一行同样位置的像素灰度为255；或者若当前像素灰度为255，且下一行同样位置的像素灰度为0，则计算当前像素点的Hough 参数(ρ，θ)，即仅统计矩形样点的上下边缘像素。因此，这改进的Hough 算法仅适合矩形样点，不适合圆形样点。按照上述的判别准则，以二值图像的中心为计算原点，以对角线长度为ρ 轴最大值，步长为1；以5°为θ 轴的最大值，步长为0.01°，计算Hough 参数空间。统计(ρ，θ)参数空间中各正弦曲线角度的信号累加值，对应着各个角度上特征点的累计数量。

1.1.3 提取占主导的直线组

无论是准则图像还是倾斜图像，同一行矩形样点的上(下)边缘都处在同一条直线上，故可以通过累计同一行样点的上(下)边缘长度，来判别该行样点是否对图像倾斜贡献较大。显然，占主导地位的都是累计长度较长的直线，对应的矩形样点行信号强度好、样点数量多。

在提取占主导地位的样点上(下)边缘之前，选择图像宽度的1/10 为最小直线长度Amin。遍历Hough 参数空间，若参数空间坐标(ρi，θj)的累加值为A(i，j)，代表直线xcos θj+ysin θj=ρi的累计长度为A(i，j)。若线长度A(i，j)小于Amin，则表明该直线不占主导地位，应舍去不记录。反之，若线长度A(i，j)不少于Amin，则要进一步判别它是否局部极大值。根据检测精度确定合理的局部峰值半径r，将Hough 参数空间中A(i，j)的r×r 邻域值与当前累加值A(i，j)比较，若A(i，j)在局部区域内仍是极大值，则表明该直线起主导作用，应保存并用于下一步计算。

1.1.4 计算直线组的平均倾斜角度

其中：Rm为直线的相对长度；θm为直线的倾斜角度；相对长度不少于0.5 的直线有M 条。

1.2 改进的Radon 变换

虽然Hough 直线检测能很好地应用在矩形样点图像上，但是Hough 圆形检测在圆形样点图像的倾斜检测上不具优势。图像中的圆形样点很少是标准的圆形，样点边缘经常有缺口或样点内部存在空洞，容易引起Hough 圆形检测的漏检[25]。其次，在存储空间方面，由于Hough 圆形检测存在3 个参数，导致建立累加器所需要空间是Hough 直线检测的平方级[26]。因此，圆形样点的芯片图像不适宜使用Hough 变换来检测倾角。考虑到检测精度和运算存储空间的关系，本算法选择选用了Radon 变换[27-28]。

针对圆形样点的形状特征和分布规律，对Radon变换进行了改进。在提取生物芯片图像中圆形样点的边缘后，对边缘图像进行二级Radon 变换，通过搜索得到最佳校正角度。它能精确地检测出规则或不规则的圆形样点图像的倾斜角度[29]，同时减少了Radon 参数空间的存储量，并提高了运算速度。

1.2.1 提取样点边缘

在检测倾斜角度之前，先对生物芯片图像进行灰度化，然后进行一次形态学的开闭运算级联操作。接着选择Otsu 算法自动计算最佳分割阈值，并使用这阈值将芯片图像二值化。灰度化与二值化的方法跟Hough 变换中所用方法是一样的。

由于Radon 变换的计算量较大[30-31]，为了减少检测的计算量，在进行Radon 变换之前，先提取圆形样点的边缘。使用最小的结构元B 对原二值图像A 进行腐蚀，再用原二值图像A 减去腐蚀图像εB(A)，即可得到边缘图像β(A)=A-εB(A)，且其边缘宽度为1。对比提取边缘前后的Radon 参数空间可知：提取边缘后得到的正弦图的整体亮度减弱，即正弦曲线的数量减少，但具体位置未变，故仍能很好地代表样点投影信号。通过精简正弦图来减少计算量，保持了准确度而又不影响检测效果，这就是Radon 变换的初步改进。

1.2.2 二级Radon 变换

Radon 变换一般将图像的中心位置作为投影原点，采用其离散形式[32-33]，投影信号表达式为：

其中：(x，y)为二值边缘图像中的坐标；(ρ，θ)为Radon参数空间中的坐标， x，y，ρ，θ 均为离散变量。固定θ 为θk，通过覆盖图像所要求的ρ 的所有值产生一个投影g(ρ，θk)。改变θ 并重复上述过程，则产生另外的投影。最终得到以ρ，θ 为变量的二维数组g(ρ，θ)，并可以利用这数组合成正弦图，而正弦图中像素的亮点与对应的g 成正比。

针对圆形样点边缘进行的Radon 变换，如果检测精度较高时，计算量的数量级也相应增加。为了减少搜索次数，本算法采用二级不同尺度的搜索策略[34]，先进行粗略搜索，在确定大致范围后再进行精细搜索。

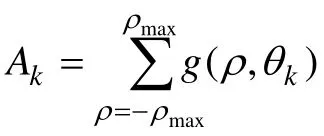
不同尺度的搜索策略在很多倾斜校正的算法中都有体验，其减少存储空间、提高运算速度的作用是显而易见的。大量实验证明，采用二级Radon 变换算法后计算量明显减少，要比同样精度的直接Radon 变换的计算量少一半以上。

2 实验与讨论

2.1 针对矩形样点改进的Hough 变换的效果

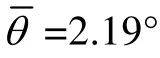
图1 改进的Hough 变换的效果图Fig.1 Effect of improved Hough transform

实验表明改进的Hough 变换在检测精度、存储空间和运算速度方面有良好的表现，非常适合用于矩形样点图像的倾角检测。对于长×宽为2 668×1 813 的矩形样点芯片图像，运用本文改进的Hough 变换和同类的算法进行倾角检测，实验数据如表1 所示。改进的Hough 变换仅需耗时4.730 s，得到的检测结果2.19°与实际倾角2.15°相差仅为0.04°，算法误差范围为±0.05°，效率和准确度比同类的算法更优越。而对于没有经过改进的Hough 变换，检测耗时为15.019 s，检测结果为2.1°，检测误差范围为±0.1°。对比前后2种Hough 变换的检测速度和误差范围可见：本文对Hough 变换的改进和优化的效果明显，仅统计矩形样点的上下边缘像素的Hough 参数和累计值，不但大大减少Hough 变换运算的次数，而且有效地减少误差范围；提取占主导地位的直线组，能避免对局部极大值点的误判，且有效地减少背景噪声对检测的干扰。

2.2 针对圆形样点改进的Radon 变换的效果

为了验证改进的Radon 变换的检测精度和速度，现已知一幅长×宽为2 713×1 820 的圆形样点芯片图像的倾斜角度为1.55° (以逆时针为旋转正方向)，其局部截图如图2(a)所示，运用改进的Radon 变换进行倾角检测。对原芯片图像进行边缘提取，其局部截图如图2(b)所示。提取到的圆形样点的边缘清晰可见，大部分样点的形状饱满，行列间隙中基本不存在噪声，非常适合Radon 投影。对二值边缘图像进行第一级Radon 变换，在[-5°，5°]区间内θ 以0.1°为步长，进行第一级Radon 变换得到初级倾斜角度θm=1.6°，对应的Radon 参数空间的截图如图2(d)所示。然后在[1.50°，1.70°]区间内θ 以0.01°为步长，进行第二级Radon 变换得到精确度更高的二级倾斜角度θm=1.58°，对应的Radon 参数空间的截图如图2(e)所示。即得最佳的倾斜校正角度为-1.58°，对倾斜图像进行旋转校正，运用双线性内插方法对旋转后的图像进行反向映射，得到校正后的图像如图2(c)所示。

表1 对矩形样点芯片图像进行倾角检测的实验结果Table 1 Experimental results of inclination detection of microarray image with rectangular spots

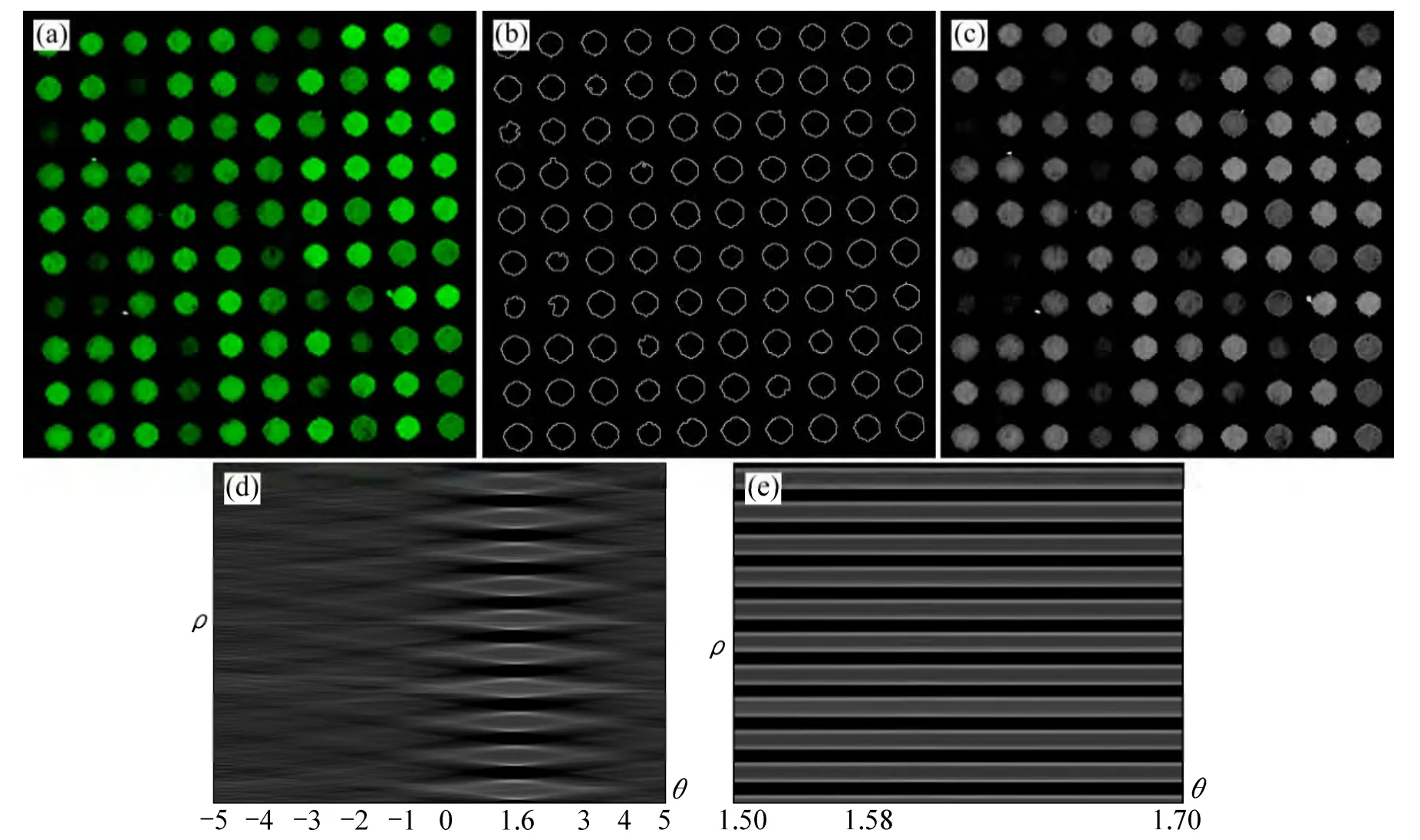
图2 改进的Radon 变换的效果图Fig.2 Effect of improved Radon transform

实验表明改进的Radon 变换在检测精度、存储空间和运算速度方面有良好的表现，非常适合用于圆形样点图像的倾角检测。对于长×宽为2 713×1 820 的圆形样点芯片图像，运用本文改进的Hough 变换和同类的算法进行倾角检测，实验数据如表2 所示。改进的Radon 变换仅需耗时5.137 s，得到的检测结果1.58°与实际倾角1.55°相差仅为0.03°，算法误差范围为±0.04°；与同类算法相比，它能在更短的时间内得到更精确的结果。而对于没有经过改进的Radon 变换，倾角检测耗时为21.659 s，得到的检测结果为1.6°，检测误差范围为±0.1°。比较检测的速度和误差范围可见，本文对Radon 变换的改进和优化的效果明显，提取圆形样点的边缘能大大减少Radon 变换投影运算的次数，且有效地减少检测误差；从粗到细的二级Radon变换将Radon 参数空间所占的内存大大减少，并将检测精度提高到0.01°。

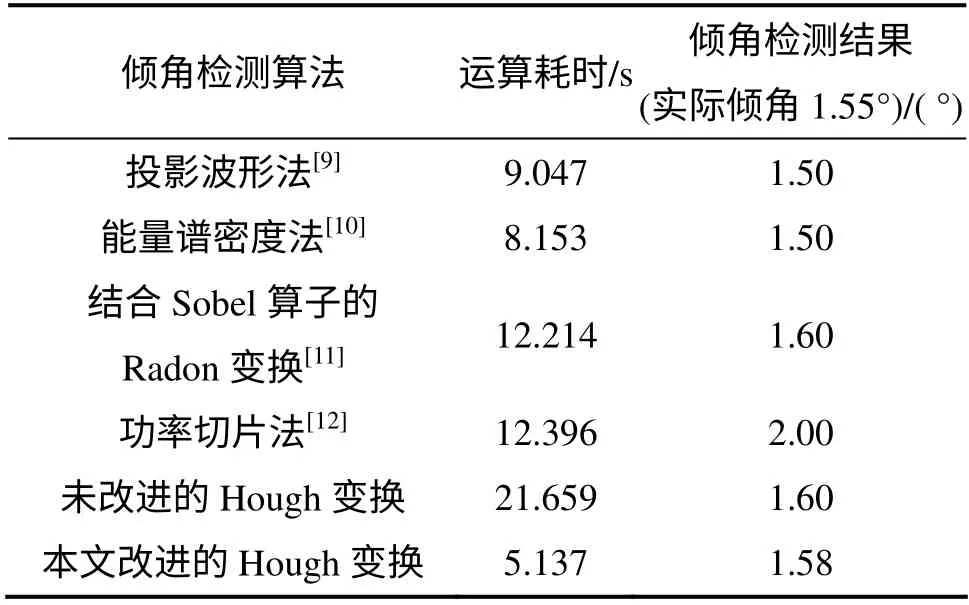
表2 对圆形样点芯片图像进行倾角检测的实验结果Table 2 Experimental results of inclination detection of microarray image with circular spots

3 结论

(1) 针对矩形样点和圆形样点各自的形状和空间分布特点，使用不同的方法分别检测矩形和圆形样点的芯片图像，提出对矩形样点图像采用改进的Hough变换检测倾角，而对于圆形样点则采用改进的Radon变换，从而实现生物芯片图像倾角的精确、快速检测。

(2) 本算法将倾角检测精度提高到0.01°，检测误差范围控制在±0.05°，对倾斜生物芯片图像的检测和校正取得满意的效果，成功地解决现有方法中倾角检测精度和速度不佳的问题。

[1] Bajcsy P. An overview of DNA microarray grid alignment and foreground separation approaches[J]. Eurasip Journal on Applied Signal Processing, 2006, 2006: 1-13.

[2] Giannakeas N, Kalatzis F, Tsipouras M G, et al. Spot addressing for microarray images structured in hexagonal grids[J]. Comput Methods Programs Biomed, 2012, 106(1): 1-13.

[3] Belean B, Borda M, Le Gal B, et al. FPGA based system for automatic cDNA microarray image processing[J]. Comput Med Imaging Graph, 2012, 36(5): 419-429.

[4] Le Brese C, Ju J Z. Automatic gridding of rotated microarray images[C]//International Conference on Biomedical and Pharmaceutical Engineering, 2006 (ICBPE 2006). Singapore,2006: 34-38.

[5] Bracewell R N, Bracewell R. The Fourier transform and its applications[M]. New York: McGraw-Hill, 1986: 65-79.

[6] Honsinger C W, Jones P W. Method for image skew detection:US, 8160393[P]. 2012-04-17.

[7] Aithal P K, Rajesh G, Acharya D U, et al. A fast and novel skew estimation approach using radon transform[J]. International Journal of Computer Information Systems and Industrial Management Applications, 2013, 5: 337-344.

[8] Wang Y, Shih F, Ma M. Precise gridding of microarray images by detecting and correcting rotations in subarrays[C]//Proceedings of the 8th Joint Conference on Information Sciences.Newark, CA, 2005: 1195-1198.

[9] Meyenhofer F, Schaad O, Descombes P, et al. Automatic analysis of microRNA Microarray images using Mathematical Morphology[C]//29th Annual International Conference of the IEEE Engineering in Medicine and Biology Society. Lyon, 2007:6235-6238.

[10] Deng N, Duan H. An automatic and power spectra-based rotate correcting algorithm for microarray image[C]//27th Annual International Conference of the Engineering in Medicine and Biology Society. Shanghai, 2006: 898-901.

[11] 刘艳, 张勇德. 含弱信号点微阵列图像的自动网格划分[J].中国医学工程, 2008, 16(3): 221-227.LIU Yan, ZHANG Yongde, SHA Xianzheng. Automatic recognition of microarray images using projection algorithm[J].China Medical Engineering, 2008, 16(3): 221-227.

[12] 严伟, 胡松, 吴钦章, 等. 生物芯片图像微阵列偏转角度计算及样点分割算法[J]. 光电工程, 2007, 34(10): 6-10.YAN Wei, HU Song, WU Qinzhang, et al. Computation for deflection angle of microarray signal and image segmentation of biochip[J]. Opto-Electronic Engineering, 2007, 34(10): 6-10.

[13] Haff R P, Quinones B, Swimley M S, et al. Automatic image analysis and spot classification for detection of pathogenic Escherichia coli on glass slide DNA microarrays[J]. Computers and Electronics in Agriculture, 2010, 71(2): 163-169.

[14] Bariamis D, Maroulis D, Iakovidis D K. Unsupervised SVM-based gridding for DNA microarray images[J]. Comput Med Imaging Graph, 2010, 34(6): 418-425.

[15] Duda R O, Hart P E. Use of the Hough transformation to detect lines and curves in pictures[J]. Communications of the ACM,1972, 15(1): 11-15.

[16] Herout A, Dubská M, Havel J. Real-time detection of lines and grids[M]. London: Springer, 2013: 3-16.

[17] Bidaut G, Manion F J, Garcia C, et al. WaveRead: automatic measurement of relative gene expression levels from microarrays using wavelet analysis[J]. Journal of Biomedical Informatics,2006, 39(4): 379-388.

[18] Amin A, Fischer S. A document skew detection method using the Hough transform[J]. Pattern Analysis & Applications, 2000, 3(3):243-253.

[19] Nandini N, Murthy K S, Kumar G H. Estimation of skew angle in binary document images using hough transform[J]. World Academy of Science, Engineering and Technology, 2008, 42:44-50.

[20] Farrahi Moghaddam R, Cheriet M. A multi-scale framework for adaptive binarization of degraded document images[J]. Pattern Recognition, 2010, 43(6): 2186-2198.

[21] Cheng H D, Shan J, Ju W, et al. Automated breast cancer detection and classification using ultrasound images: A survey[J].Pattern Recognition, 2010, 43(1): 299-317.

[22] Otsu N. A threshold selection method from gray-level histograms[J]. IEEE Transactions of Systems, Man, and Cybernetics, 1979, SMC-1(1): 62-66.

[23] 邵桂芳, 李刚, 李铁军, 等. 基因芯片图像高亮噪声处理算法研究[J]. 厦门大学学报(自然科学版), 2009, 48(3): 331-333.SHAO Guifang, LI Gang, LI Tiejun, et al. Methods for highly fluorescent noise reduction in microarray images[J]. Journal of Xiamen University (Natural Science), 2009, 48(3): 331-333.

[24] Angulo J, Serra J. Automatic analysis of DNA microarray images using mathematical morphology[J]. Bioinformatics, 2003,19(5): 553-562.

[25] Sun H, Mao Y, Yang N, et al. A real-time and robust multi-circle detection method based on randomized Hough transform[C]//International Conference on Computer Science and Information Processing (CSIP). Xi’an, 2012: 175-180.

[26] Chattopadhyay K, Basu J, Konar A. An efficient circle detection scheme in digital images using ant system algorithm[C]//Proceedings of the 2008 IEEE Sponsored Conference on Computational Intelligence, Control And Computer Vision in Robotics & Automatic. Rourkela, India, 2008: 145-148.

[27] Bariamis D, Iakovidis D K, Maroulis D. M3G: maximum margin microarray gridding[J]. Bmc Bioinformatics, 2010, 11(1):49-59.

[28] Rueda L, Rezaeian I. A fully automatic gridding method for cDNA microarray images[J]. Bmc Bioinformatics, 2011, 12(1):113-129.

[29] Antoniol G, Ceccarelli M, Petrosino A. Microarray image addressing based on the radon transform[C]//IEEE International Conference on Image Processing, 2005 (ICIP 2005), 2005: 1-13.

[30] Ceccarelli M, Antoniol G. A deformable grid-matching approach for microarray images[J]. IEEE Trans Image Process, 2006,15(10): 3178-3188.

[31] Brändle N, Bischof H, Lapp H. Robust DNA microarray image analysis[J]. Machine Vision and Applications, 2003, 15(1):11-28.

[32] Beylkin G. Discrete radon transform[J]. Acoustics, Speech and Signal Processing, IEEE, 1987, 35(2): 162-172.

[33] Dai X B, Shu H Z, Luo L M, et al. Reconstruction of tomographic images from limited range projections using discrete Radon transform and Tchebichef moments[J]. Pattern Recognition, 2010, 43(3): 1152-1164.

[34] 李政, 杨扬, 颉斌, 等. 一种基于Hough 变换的文档图像倾斜纠正方法[J]. 计算机应用, 2005, 25(3): 584-585.LI Zheng, YANG Yang, XIE Bin, et al, et al. Skew angle detection and correction of document images based on Hough transform[J]. Computer Applications, 2005, 25(3): 584-585.