岩石亚临界裂纹扩展应力强度因子Williams 级数计算及数值模拟

郝瑞卿，李江腾，曹平，廖峻，刘博

(中南大学 资源与安全工程学院， 湖南 长沙，410083)

近年来，人类修建的岩土工程规模不断扩大，为保证这些工程的顺利进行以及工程结束后使用的稳定性、安全性，要求岩体工程能保持长期的稳定性。根据断裂力学原理，在岩体裂纹尖端的应力强度因子KⅠ未达到其断裂韧度 KIC时，裂纹会以一种较稳定的速度向前扩展，这种岩石裂纹稳定的、准静态扩展方式称为岩石的亚临界扩展。而当亚临界扩展进行到一定程度时，通常岩石内裂纹将会快速扩展，进而发生断裂，导致岩土工程失稳，说明岩土工程的稳定性与岩石裂纹扩展的时间相关：因此，研究岩石亚临界裂纹扩展规律对岩石稳定的时间相依性研究具有重要意义。目前，已有许多学者对岩石亚临界裂纹扩展进行了试验研究，如肖洪天等[1]对三峡船闸高边坡花岗岩进行了双扭试验，得到了花岗岩亚临界裂纹扩展速度与应力强度因子之间的关系；张雯等[2]分析了岩石亚临界裂纹扩展的应力腐蚀机理，认为亚临界扩展是由拉应力和裂纹尖端物质与环境中的腐蚀介质发生化学反应使化学键断裂这2 种机制联合作用的结果，并测试了金川矿区的3 种岩样，得到了应力强度因子与裂纹扩展速度之间的关系。袁海平等[3]对金川矿区的软弱复杂矿岩进行了双扭试验，得到矿岩的断裂韧度及应力强度因子与裂纹扩展速度之间的线性关系；陈瑜等[4-7]对岩石亚临界裂纹扩展进行了实验研究，并得到裂纹扩展的停滞速度和门槛值。汪亦显等[8]得到了含水率较大的岩石亚临界裂纹扩展中应力强度因子与裂纹扩展速度的关系。上述研究均是从双扭试验中应力强度因子与柔度和应变能释放率之间的关系推导出应力强度因子的求解公式。本文作者运用Williams 级数，对双扭试验中应力强度因子的数值解进行推导，并在上述学者所做试验研究的基础上，应用ANSYS 数值模拟软件对岩石亚临界裂纹扩展进行数值模拟，将3种方法所得应力强度因子进行比较和分析，以便为岩土工程稳定的时间相依性研究提供基本参考。

1 双扭试验的基本原理

双扭试验是测试亚临界裂纹扩展速度的一种直接方法，它能够直观地监测裂纹的扩展过程，加载及预裂方式简单有效，适用性广，并且在确定应力强度因子KⅠ时不需知道裂纹的长度，因此，该方法成为研究亚临界裂纹扩展的有效手段。双扭试件最先应用于研究玻璃、陶瓷等脆性材料的断裂特性，Ciccotti 等[9-12]将其应用于岩石材料，研究其断裂韧度及亚临界裂纹扩展规律。

图1 所示为双扭试件示意图。该试件为一矩形薄板，在板的下表面沿长度方向的对称线开有1 条通槽，以使加载时裂纹沿该槽扩展。

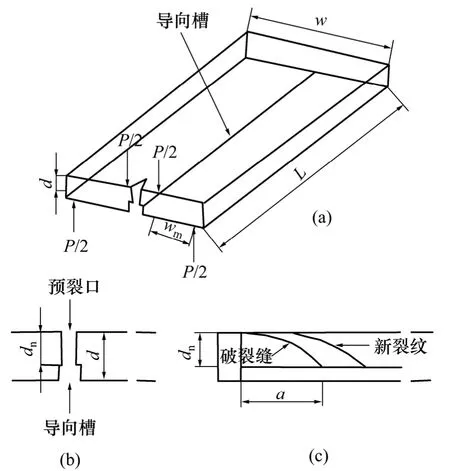
图1 双扭试件示意图Fig.1 Schematic diagrams of double torsion specimen

双扭试件可以看作由2 个弹性扭转杆组成。对于小变形，且宽度远大于试件厚度的双扭试件，裂纹尖端的应力强度因子KI[9-12]为

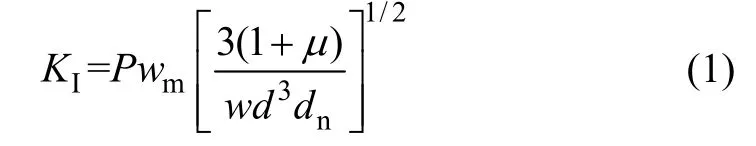
式中：P 为作用于扭杆上的荷载；wm为扭臂的长度；μ 为泊松比；d 为试件的厚度；dn为试件厚度与通槽厚度之差；w 为试件的宽度。

式(1)为计算应力强度因子所用公式，可知应力强度因子与荷载、试件尺寸和泊松比等因素有关，而不依赖于裂纹长度a。

2 双扭试验裂纹尖端应力强度因子Williams 级数解

2.1 作用力的转换

由图1 可知：虽然双扭试验中试件端部受到力偶作用，但试件裂纹扩展是由于裂纹面受到垂直于裂纹面的应力作用，裂纹扩展原理与Ⅰ型裂纹的扩展原理相同，故可以在力偶作用面内用1 对能产生相同裂纹扩展效果的拉力代替力偶。

力偶作用平面示意图如图2 所示。根据弹性力学基本理论[13]，力偶作用面内最大切应力τmax为

式中：M 为作用于杆端截面力偶；β为与d 和w 相关的系数。

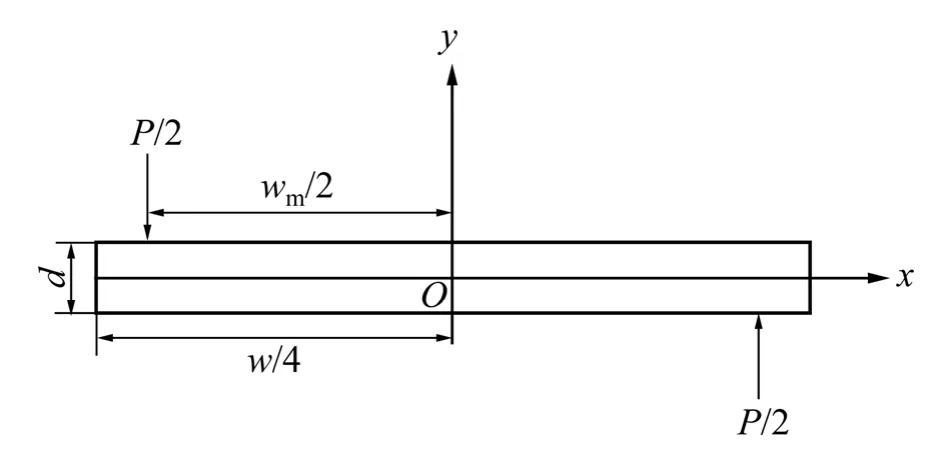
图2 力偶作用平面示意图Fig.2 Plane of couple diagram

则模型底面任一点切应力τ 为

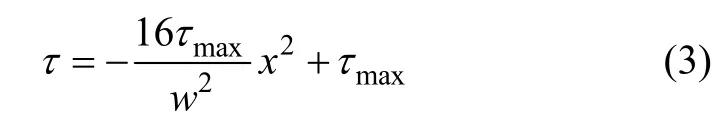
式中：x 为距坐标原点的距离；τmax为切应力τ 的最大值。可得底面切应力的合为

则模型所受到产生Ⅰ型裂纹的合力F合为

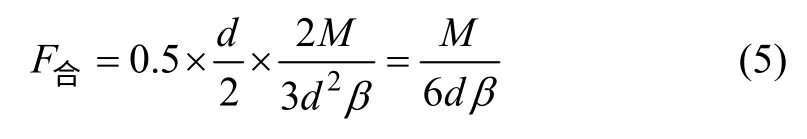
通过上述分析可知：双扭试验中裂纹的扩展由上述合力产生，故可用该力替代力偶。转换后的分析模型见图3。图3 中：P 为转换后的合力；r 和θ 为极坐标；b 为试件长度；c 为试件长度与裂纹长度之差。

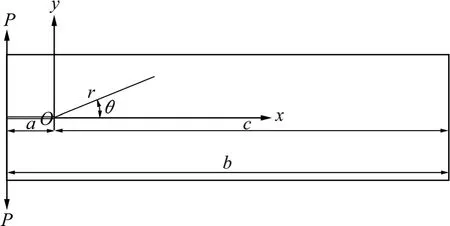
图3 力偶转换后分析模型图Fig.3 Model diagram after changing couple

2.2 Williams 级数表示的应力函数

力偶转换后，原双扭试验转换为平面问题，故可采用Williams 级数进行分析。由文献[14]知，Williams提出的无穷级数应力函数分为偶函数和奇函数2 部分，其中偶函数相当于Ⅰ型裂纹里对称加载，故可设图3 所示模型的应力函数为

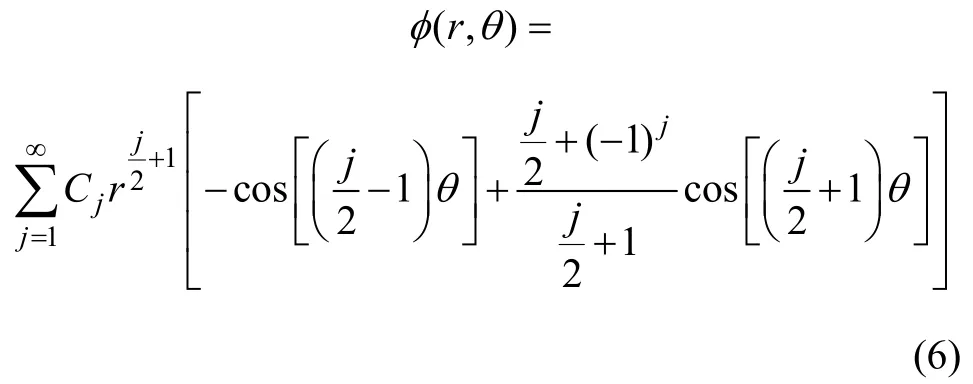
式中： φ (r,θ)为极坐标；Cj为待定系数。引入1 个无量纲系数Xj[14]，其与应力函数 φ (r,θ)中第j 项待定系数Cj的关系为

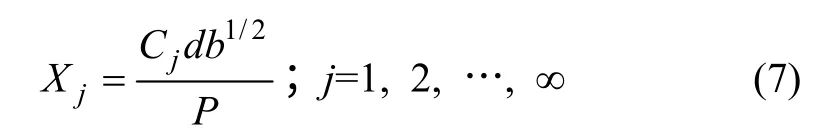
式中：b 为试件长度。根据直角坐标和极坐标的转换关系，可求得：

对于任意直角坐标系Ont 与原直角坐标系Oxy 之间夹角为ω，根据坐标系间关系可知

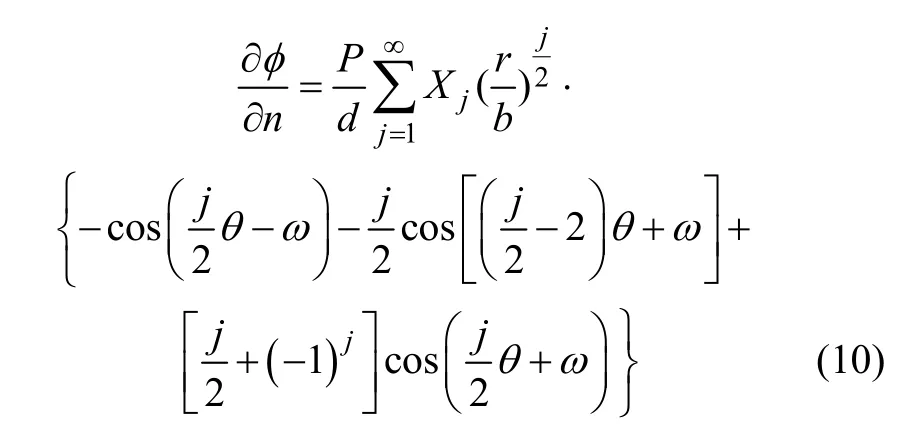
其二阶偏导数为

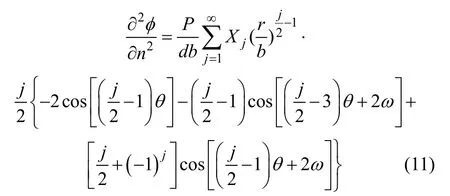
由Airy 应力分量表达式[14]可知

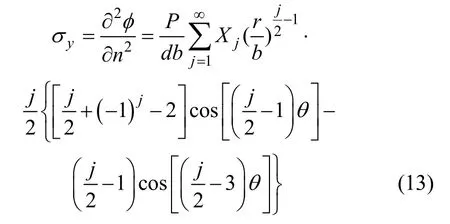
根据断裂力学原理可知

将式(13)代入，引入Williams 极数，应力强度因子KI′为

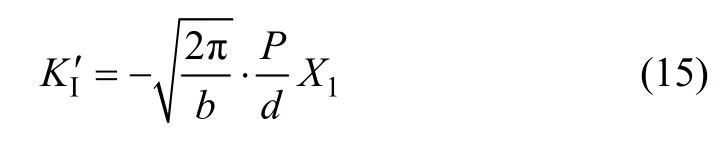
从式(15)可以看出：要解得应力强度因子KI′，必须求解无量纲系数X1。

2.3 边界配置法解方程组

在边界配置法中，为使方程可以求解，取应力函数前2m 项组成的有限级数形式的近似解代替精确解，故式(13)可改写为

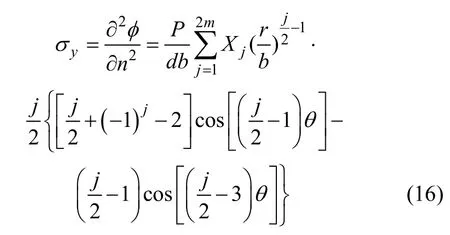
由于试样左右对称，故取1 半进行分析。根据理论力学中力的简化可知：作用于裂纹口的1 对拉力可转换为作用于模型长边中点的大小相等、方向相同的力和这个力与平移距离相乘得到的力偶。简化后的受力情况如图4 所示。

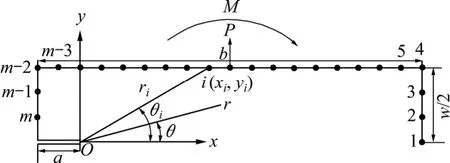
图4 配置点设置图Fig.4 Diagram of collocation points

对于被研究部分m 个配置点的设置如图4 所示，在右边界设置4 个点，编号为1，2，3 和4；左边界设置3 个点，编号为m-2，m-1 和m；在上边界设置m-7 个点，编号为5，6，…，m-3。

在边界配置法中，针对配置点建立边界条件，每个配置点有2 个边界条件，即

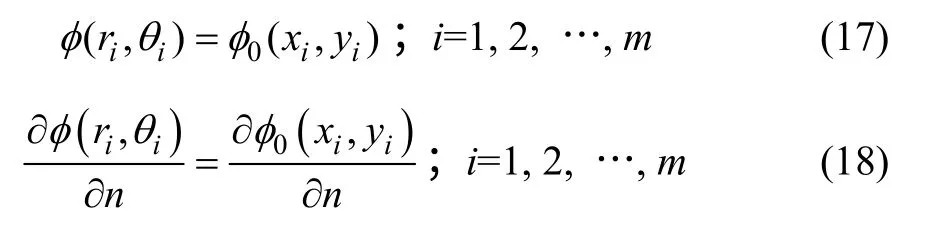
式中： φ0(xi, yi)为非裂纹体的应力函数，

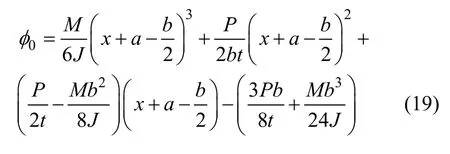
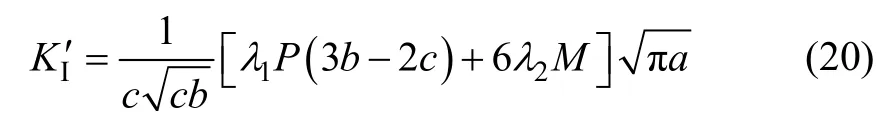
式中：c 为试件长度减去裂纹长度，即c=b-a；λ1和λ2为与a 和b 相关的系数。

2.4 算例分析

为研究该计算方法的可行性，选取大理岩和花岗岩试块为例，具体计算试件尺寸及力学参数见表1。

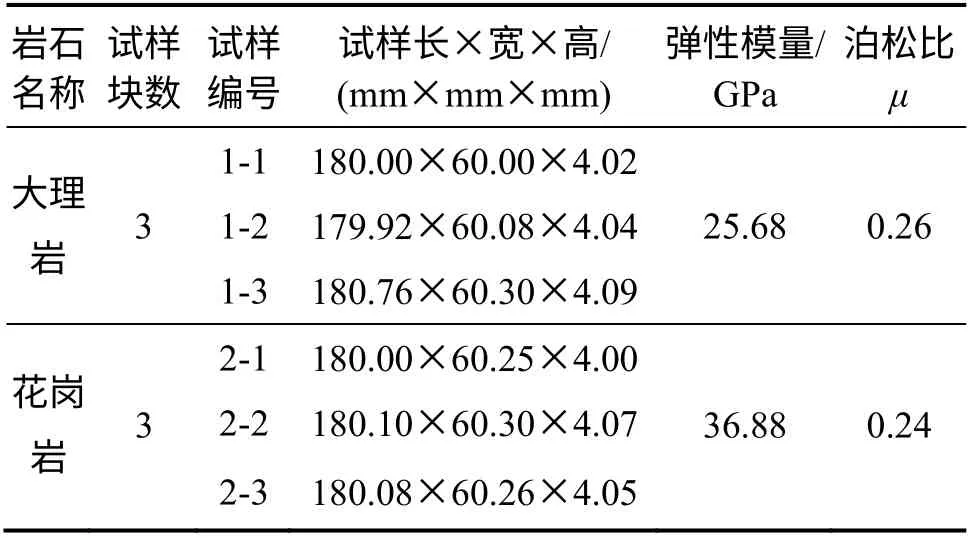
表1 试样尺寸与力学参数Table 1 Sizes and mechanical Parameters of specimens

根据李江腾[16]试验数据中不同测试点的受力，经过前述力的转换可求得此计算方法中模型所受的单位厚度的力、力矩及开裂过程中裂纹长度a。大理岩试件具体参数见表2，花岗岩试件具体参数见表3。

从表4 可以看出：此计算方法所得的应力强度因子 KI′随着裂纹长度的增加而减小，与试验测得的应力强度因子 KI变化规律相同；同时，计算所得的 KI′与试验测得的 KI比较相对较大，并且随着裂纹占试样长度比例的增大而差距增大。

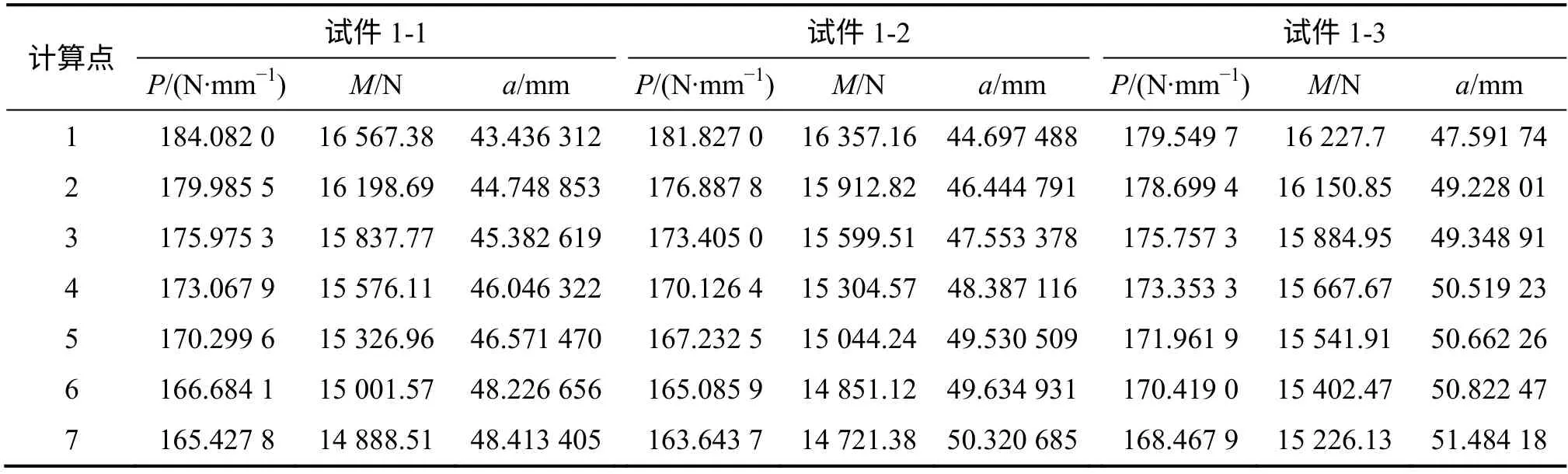
表2 大理岩试件计算点受力P、力矩M 及裂纹长度aTable 2 Force, couple and crack length of marble

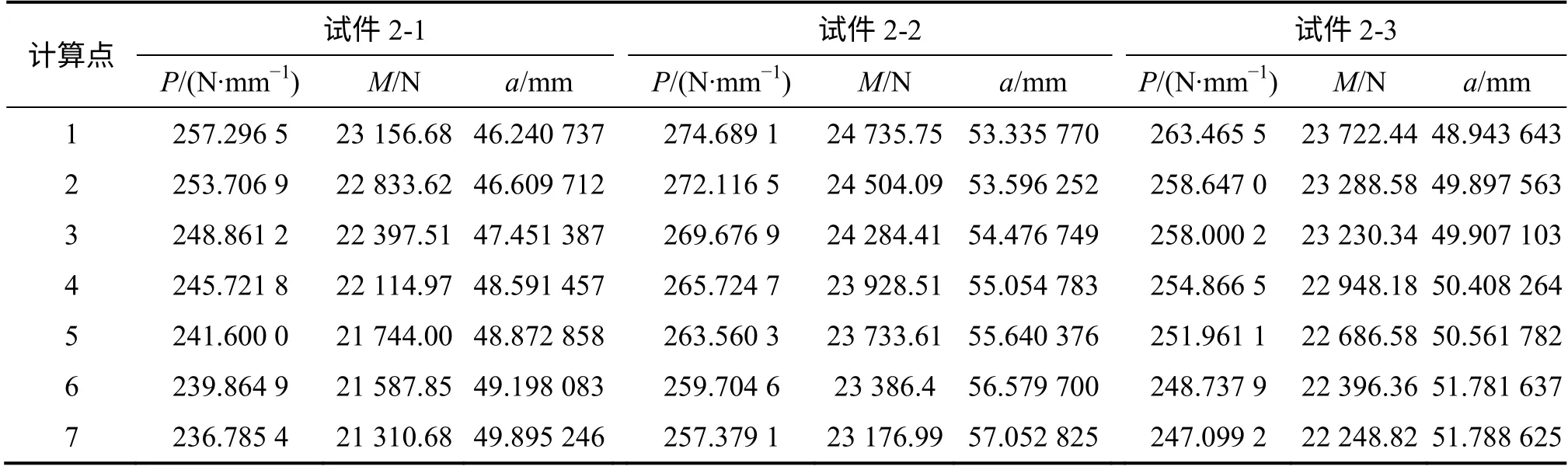
表3 花岗岩试件计算点受力P、力矩M 及裂纹长度aTable 3 Force, couple and crack length of granite

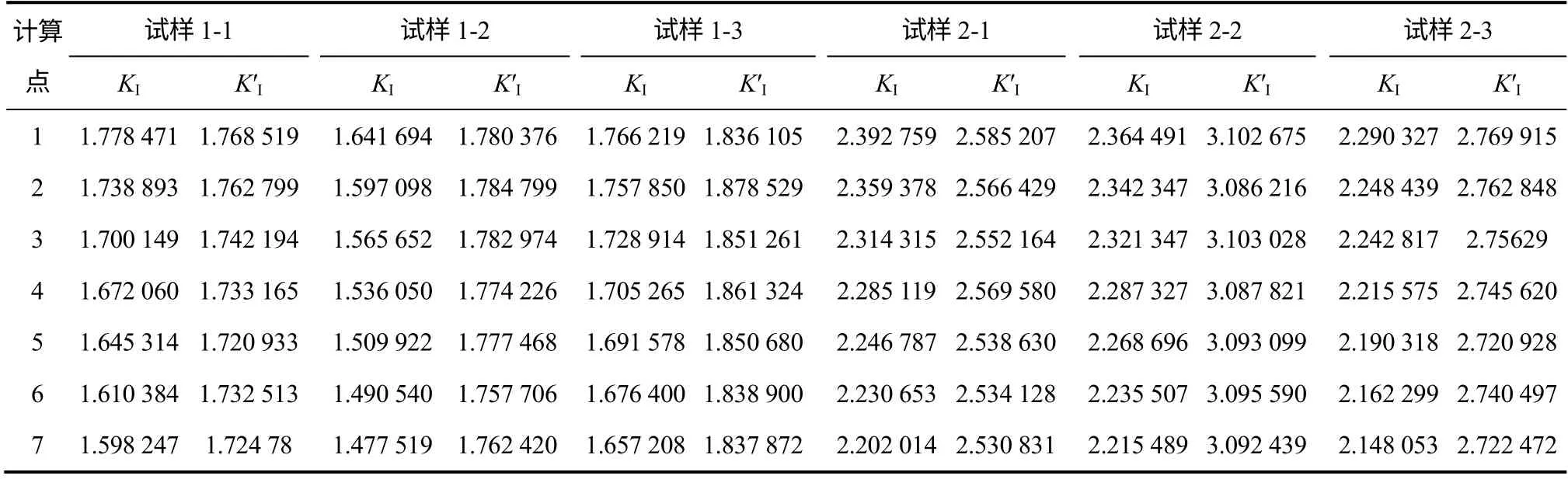
表4 试验和计算所得应力强度因子Table 4 Stress intensity factor of test and calculation MN·m-3/2

3 双扭试验的数值模拟

在试验和理论推导的基础上，本文应用ANSYS数值模拟软件，分别对上述大理岩和花岗岩试件进行常位移松弛法双扭试验的数值模拟，通过ANSYS 软件分析，分别计算大理岩和花岗岩在亚临界裂纹扩展中裂纹尖端应力强度因子 KI′。具体模拟试件尺寸及力学参数见表1。

3.1 模型的建立

使用ANSYS 计算应力强度因子，常规单元在裂纹尖端存在奇异性，为提高计算精度，本次模拟采用奇异单元，即二次三角(或五面体)单元，消除应力强度因子奇异性，提高计算精度。

由双扭试验可知，模型对称于沿长度方向所开的通槽，根据对称性，取试件整体的1/2 建立几何模型。图5 所示为试件网格划分模型。

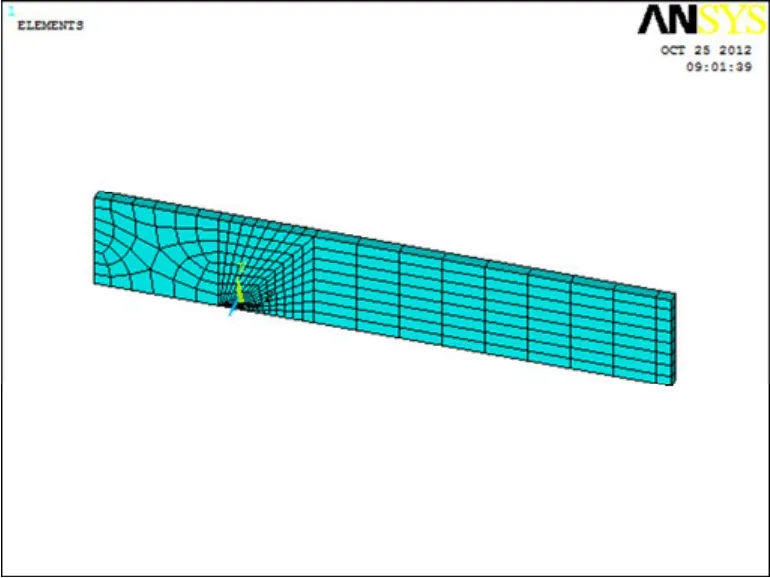
图5 试样网格划分模型Fig.5 Meshing model of sample

在裂纹尖端点处，采用奇异单元。图6 所示为裂纹尖端处网格划分模型。

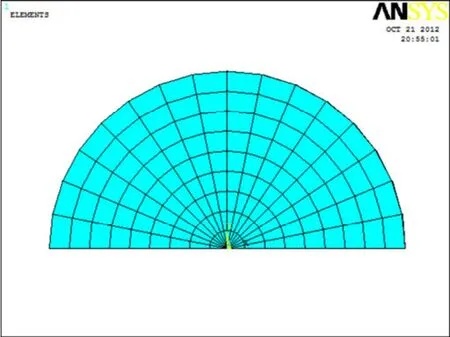
图6 裂纹尖端处网格划分Fig.6 Meshing at crack-tip

3.2 加载求解

模型加载方式为：通槽所在边界处施加对称位移约束，反映另一半未画出模型对本模型的影响；在试验加载点对模型进行z 轴方向的位移加载，模拟试验时的恒定位移；在钢珠放置点进行全位移约束，即限制钢珠放置点x，y 和z 方向的位移及转动。

在求解应力强度因子前，定义沿裂纹面的路径，以裂纹尖端作为路径第1 点，沿裂纹面定义2 个附加点，以指出裂纹扩展方向。

图7 所示为试样1-1 y 轴方向的应力云图。从图7可以看出：在裂纹尖端点处有明显的应力集中，与断裂力学理论相符。表5 和表6 所示分别为大理岩、花岗岩根据双扭试验测得的应力强度因子KⅠ以及数值模拟所得的应力强度因子 KI′。

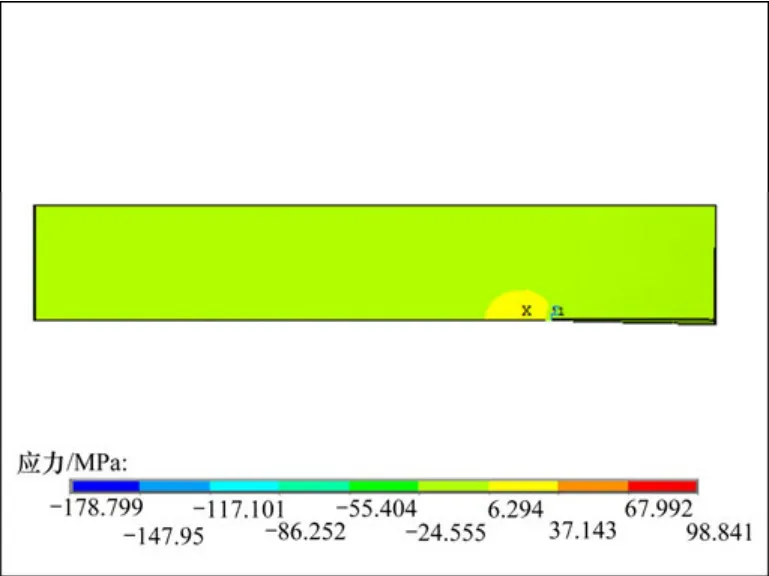
图7 试样1-1 y 轴方向的应力云图Fig.7 Stress of y axis for sample 1-1

4 理论计算、模拟与试验结果对比分析

大理岩和花岗岩根据试验测得的应力强度因子、Williams 级数法计算的应力强度因子和模拟所得的应力强度因子的变化趋势分别如图8 和图9 所示。

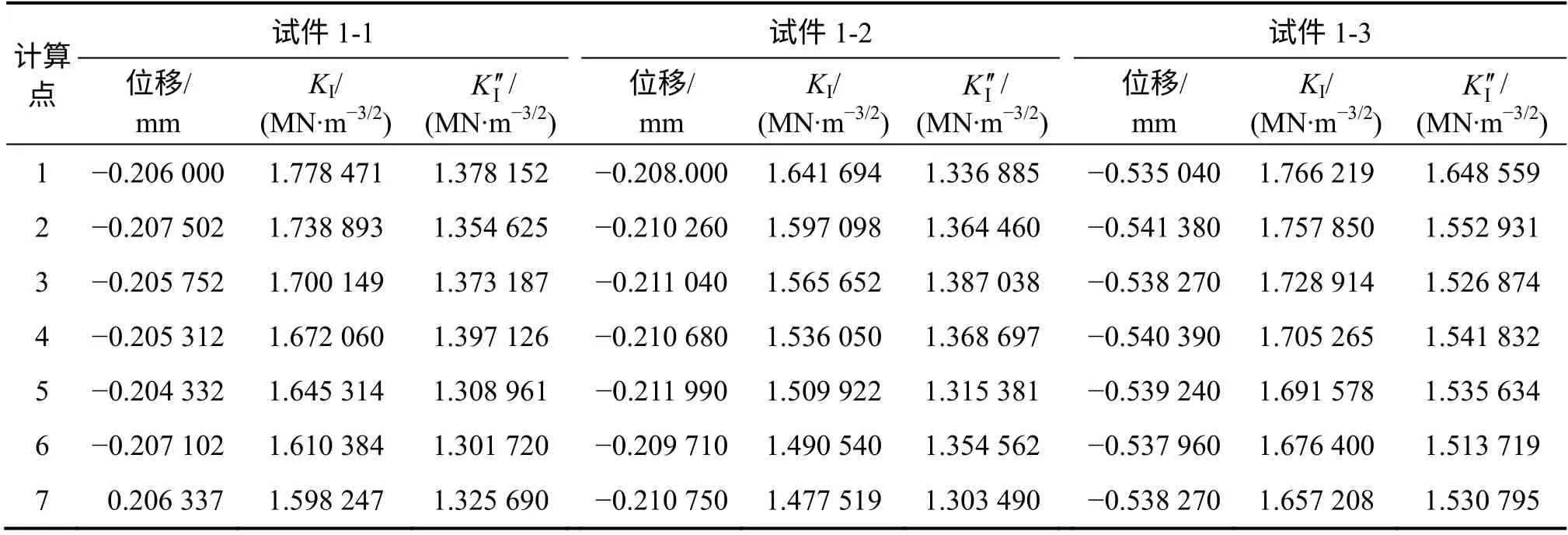
表5 大理岩应力强度因子Table 5 Stress intensity factor of marble

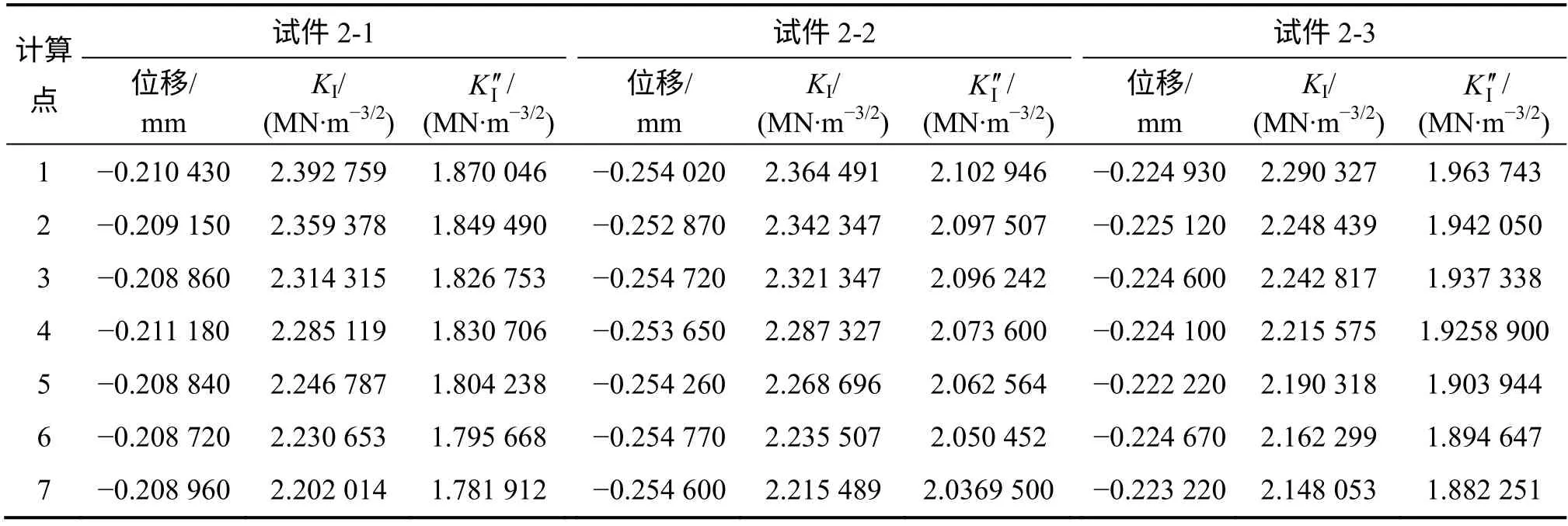
表6 花岗岩应力强度因子Table 6 Stress intensity factor of granite

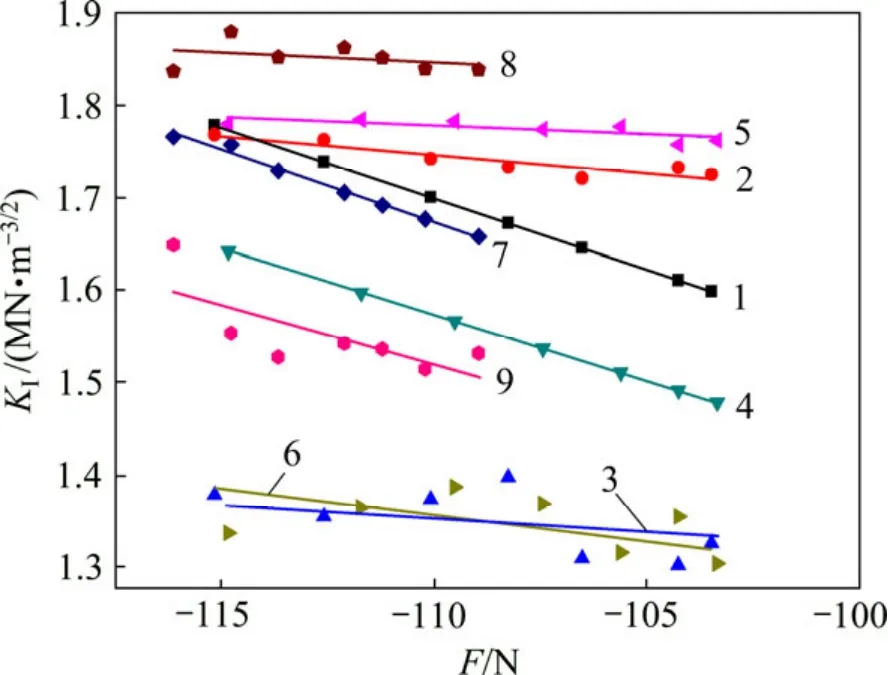
图8 大理岩应力强度因子变化趋势图Fig.8 Trend of stress intensity factor for marble

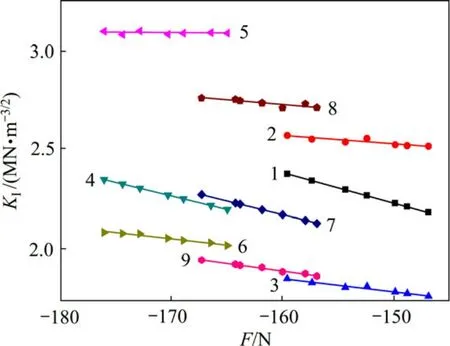
图9 花岗岩应力强度因子变化趋势图Fig.9 Yrend of stress intensity factor for granite

从图8 和图9 可以看出：岩石亚临界裂纹扩展过程中，随着裂纹的扩展，应力逐渐松弛，裂纹尖端的应力强度因子逐渐减小。

5 结论

1) 采用Williams 级数及ANSYS 数值模拟2 种方法分别对大理岩、花岗岩在双扭试验中亚临界裂纹扩展进行了理论计算和数值模拟，得到了裂纹扩展时裂纹尖端的应力强度因子，为岩土工程稳定的时间相依性研究提供了基本依据。

2) 随着裂纹的扩展，应力逐渐松弛，裂纹尖端的应力强度因子逐渐减小，此减小规律符合断裂力学的相关理论。

3) 岩石一般所处地质条件较复杂，周围环境对岩石的亚临界裂纹扩展影响如水对裂纹亚临界扩展的影响较大，这在本文Williams 级数计算和模拟分析中并没有得到体现；又如在地层深处，温度对岩石亚临界裂纹扩展的影响亦不能忽视。这些因素的影响还有待于进一步研究。

[1] 肖洪天, 杨若琼, 周维垣. 三峡船闸花岗岩亚临界裂纹扩展试验研究[J]. 岩石力学与工程学报, 1999, 18(4): 447-450.XIAO Hongtian, YANG Ruoqiong, ZHOU Weiyuan. Testing study of subcritical crack growth of granite at the Three Gorges shiplock[J]. Chinese Journal of Rock Mechanics and Engineering, 1999, 18(4): 447-450.

[2] 张雯, 曹平, 袁海平, 等. 岩石亚临界裂纹扩展的应力腐蚀[J].土工基础, 2009, 23(2): 64-67.ZHANG Wen, CAO Ping, YUAN Haiping, et al. Testing study of stress corrosion of the rock subcritical clack growth[J]. Soil Eng and Foundation, 2009, 23(2): 64-67.

[3] 袁海平, 曹平, 周正义. 金川矿岩亚临界裂纹扩展试验研究[J]. 中南大学学报(自然科学版), 2006, 37(2): 381-384.YUAN Haiping, CAO Ping, ZHOU Zhengyi. Testing study of ubcritical crack growth of ore in Jinchuan Mine[J]. Journal of Central South University (Science and Technology), 2006, 37(2):381-384.

[4] 陈瑜, 曹平, 张科, 等. 岩石亚临界裂纹扩展机制及工程门槛值研究[J]. 武汉理工大学学报, 2010, 32(19): 60-64.CHEN Yu, CAO Ping, ZHANG Ke, et al. Research on subcritical clack growth and engineering thresholds of rocks[J].Journal of Wuhan University of Technology, 2010, 32(19):60-64.

[5] 万琳辉, 曹平, 黄永恒, 等. 岩石亚临界裂纹扩展及其应用研究[J]. 科技导报, 2010, 28(9): 42-46.WAN Linhui, CAO Ping, HUANG Yongheng, et al. Subcritical crack growth of rocks and its applications[J]. Science &Technology Review, 2010, 28(9): 42-46.

[6] 李江腾, 曹平, 袁海平. 岩石亚临界裂纹扩展试验及门槛值研究[J]. 岩土工程学报, 2006, 28(3): 415-418.LI Jiangteng, CAO Ping, YUAN Haiping. Study on subcritical crack growth and thresholds of rocks[J]. Chinese Journal of Geotechnical Engineering, 2006, 28(3): 415-418.

[7] 赵延林, 曹平, 万文, 等. 岩石裂纹亚临界扩展实验与压剪流变断裂模型[J]. 中南大学学报(自然科学版), 2014, 45(1):276-286.ZHAO Yanlin, CAO Ping, WAN Wen, et al. Rock cracks subcritical propagation test and compression-shear rheological fracture model[J]. Journal of Central South University (Science and Technology), 2014, 45(1): 276-286.

[8] 汪亦显, 曹平, 陈瑜, 等. 膨胀性软岩水腐蚀损伤断裂力学效应实验研究[J]. 中南大学学报(自然科学版), 2011, 42(6):1685-1691.WANG Yixian, CAO Ping, CHEN Yu, et al. Testing study on damage and fracture mechanical effects for swelling soft rock during water corrosion[J]. Journal of Central South University(Science and Technology), 2011, 42(6): 1685-1691.

[9] Ciccotti M, Negri N, Gonzato G, et al. Practical application of an improved methodology for the double torsion load relaxation method[J]. International Journal of Rock Mechanics and Mining Sciences, 2001, 38(4): 569-576.

[10] Saadaoui M, Reynaud P, Fantozzi G, et al. Slow crack growth study of plaster using the double torsion method[J]. Ceramics International, 2000, 26(4): 435-439.

[11] Nara Y, Kaneko K. Study of subcritical crack growth in andesite using the Double Torsion test[J]. International Journal of Rock Mechanics and Mining Sciences, 2005, 42(4): 521-530.

[12] Ciccotti M, Gonzato G, Mulargia F. The double torsion loading configuration for fracture propagation: An improved methodology for the load-relaxation at constant displacement[J].International Journal of Rock Mechanics and Mining Sciences,2000, 37(7): 1103-1113.

[13] 徐芝纶. 弹性力学简明教程[M]. 北京: 高等教育出版社,2005: 173-174.XU Zhilun. A concise course in elasticity[M]. Beijing: Higher Education Press, 2005: 173-174.

[14] 袁懋昶. 断裂力学理论及其工程应用[M]. 重庆: 重庆大学出版社, 1989: 174-196.YUAN Maochang. The theory of fracture mechanics and application in engineering[M]. Chongqing: Chongqing University Press, 1989: 174-196.

[15] 李江腾. 硬岩矿柱失稳及时间相依性研究[D]. 长沙: 中南大学资源与安全工程学院, 2005: 66-77.LI Jiangteng. Study on instability and time dependence of pillar in hard rock mass[D]. Changsha: Central South University.School of Resources and Safety Engineering, 2005: 66-77.