基于蒙特卡罗模拟的区域建筑冷负荷预测模型
2014-04-01王利珍谭洪卫武涌庄智
王利珍,谭洪卫,武涌,庄智
(1. 同济大学 机械与能源工程学院,上海,200092;2. 同济大学 绿色建筑及新能源研究中心,上海,200092;3. 住房和城乡建设部 建筑节能与科技司,北京,100085)
随着城镇化的发展,国内有很多绿色生态低碳城区正在开发建设,为达到区域节能减排的目标,区域的能源规划越来越重要[1]。在规划与方案阶段,区域能源站或区域供冷系统方案的基础是负荷计算,负荷预测具有极大的随机性和未知性[2]。传统的区域负荷预测由面积指标估算法叠加来确定,或者通过估计输入条件由能耗模拟软件进行模拟,带有极大的经验成分。当前,国内外有关单体建筑的负荷计算和能耗计算研究较多,主要包括神经网络法[3-4]、统计回归法[5]、支持向量机法[6]和灰色理论结合改进的遗传算法[7]等,Yao 等[8]等应用组合预测方法将常用的几个空调负荷预测模型有机结合起来,并引入层次分析法建立了空调负荷组合预测的结构模型,这些方法都能在设计阶段对单体建筑进行预测。在建筑设计初期很多因素影响建筑负荷计算,Dominguez-Munozd 等[9]研究单体建筑峰值负荷的不确定性。同样,区域建筑冷负荷具有不确定性和动态变化特性。情景分析法[10]通过设定几种情景,来预测区域冷热负荷,但还存在不确定性。蒙特卡罗模拟的实质是通过大量的随机试验,利用概率论解决问题的一种数值方法[11]。近年来,国内外学者对蒙特卡罗模拟方法进行了大量研究,其主要应用于经济学与金融学、建筑物热模拟、风力发电机、医学统计和可靠性等方面[11-14]。本文作者首先搭建区域建筑冷负荷预测模型,并基于此确定随机变量函数分布,进而采用蒙特卡罗数值模拟方法来解决在规划阶段区域建筑冷负荷的诸多不确定性,进行区域冷负荷预测,以便最终为规划阶段能源系统方案的优化设计和电力规划提供数据和方法支撑,降低风险投资。
1 蒙特卡罗数值模拟方法
蒙特卡罗数值模拟法是通过抽样统计原理建立一个数学或物理模型,从而解决实际问题。本文应用蒙特卡罗数值模拟方法的基本思路为:
第1 步,建立描述区域建筑冷负荷数学模型;
第2 步,确定蒙特卡罗分析模型的主要风险变量,通过调研统计分析确定各个风险变量的概率分布;
第3 步,编制程序按照给定的概率分布抽样生成大量的随机数,这些随机数可以模拟实际问题中随机因素的变化;
第4 步,将这些随机数作为各变量的参数代入随机模型,求出区域建筑冷负荷(即模型的输出变量),经过大量的模拟计算,得到输出变量的计算特征值,从而预测在众多因素影响下的区域建筑冷负荷峰值及其概率分布。
针对本问题,采用Matlab[15]编制程序来实现蒙特卡罗随机模拟,过程见图1。

图1 蒙特卡罗模拟方法流程图Fig.1 Flowchart of Monte Carlo simulation method
2 区域建筑冷负荷预测随机模型
2.1 区域建筑冷负荷预测模型
从建筑形态来看,建筑大多数以长方体或者多个长方体组合而成,本文选用长方形作为建筑的底面形状来进行研究。区域建筑冷负荷的问题可以表述为:在某个区域内有n 类建筑,规划图中各类建筑的功能定位、建筑面积、限高等已确定,简化建筑内部布局分隔将同类建筑看成一个整体,在简易方法[16]的基础上采用冷负荷系数法[17]结合区域建筑负荷不确定性因素,建立区域建筑冷负荷预测随机模型:






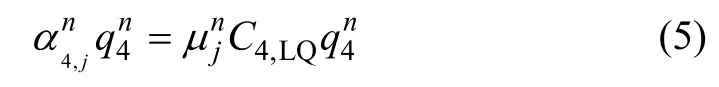

2.2 预测模型关键参数及其概率分布

对规划区所在城市的既有建筑进行问卷调研,结合当地的统计年鉴,同时将未来发展趋势和要求等预测参数设定于随机变量的分布函数中,可得到各项随机变量的隶属度函数。如外墙传热系数分布函数的确定,通过资料调研获得常用的外墙构造以及外墙的传热系数,利用统计学方法可获得外墙的传热系数服从正态分布。

随机变量 分布θIn 均匀分布K1,K2,K3正态分布n dp均匀分布q4,q5n三角形分布n Gn,ε离散型分布
2.3 随机变量的抽样方法
采用反函数法对连续型和离散型随机变量进行直接抽样。
2.3.1 连续型随机变量
对于随机变量X 的分布函数F(x)可以求其反函数G(x),若R 为在[0,1]区间内均匀分布的随机变量,则通过X=G(R)变换,即可得到按F(x)分布的随机变量X。按此方法,可得到三角形分布和均匀分布的变换式X=G(R)。
1) 三角形分布。变量X 概率分布密度函数为

经积分计算得到其分布函数为
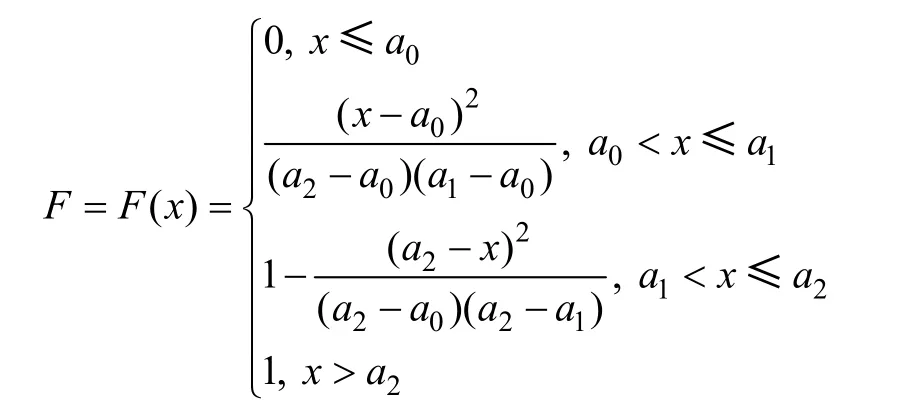
设R 为[0,1]上均匀分布的随机数,三角形分布模型变量X 随机抽样的变换式为

2) 均匀分布:

随机变量X 的分布密度为
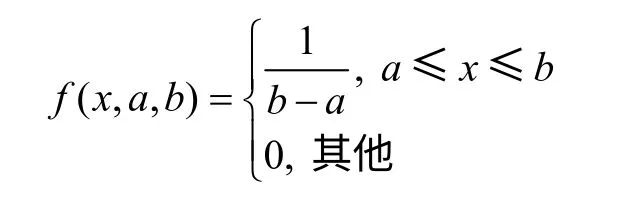
X 服从区间[a,b]上的均匀分布,X~U[a,b]。
3) 正态分布采用Box-Muller 法得到。设R1,R2是区间[0,1]上均匀分布的随机变量,且相互独立。变换式为

x1和x2服从N(0,1)分布,且相互独立。通过公式x =μ+x1×σ变换,即可得到服从 N (μ ,σ )分布的随机变量X。
2.3.2 离散型随机变量

2.4 随机模型的输入和输出
随机模型的输入项和输出项见图2。
3 仿真分析与实际案例
3.1 案例
以夏热冬暖地区某规划区为研究区域(图3),拟打造为办公、宾馆、商业、医疗卫生、教育和住宅为一体的综合行政区,以河以西同期开发的区域为研究对象,利用蒙特卡罗数值模拟法预测该区域建筑冷负荷。

图2 随机模型输入和输出构架Fig.2 Composition of input and output parameters on stochastic model
3.2 随机模型的参数确定
随机模型的输入参数包括确定性参数和随机变量,确定性参数取值方法见表2。随机变量的确定需要对既有城区各类建筑开展调研,调研内容包括当地的经济水平、产业结构、人口状况,在各类建筑中选取部分建筑,调查用户的建筑信息、围护结构、用户信息、当地常规能源、用能模式、能源价格,新能源补贴政策等,建立该地的能耗信息基础数据库。通过Matlab 编制程序产生随机数,如办公类建筑的照明功率密度服从三角形分布,模拟过程中产生随机数如图4 所示。

参数 备注AnA(3A=12=53 76 4009,0A,4A=26=15 64 2470,0,A5=1 296,A6=679 025,m2),h,h0,a,m新区规划图中国建筑热环境分析专用气象数据集θw,hw,Dj,max,Δt1,Δt2,Δt3,hw,φn,λn j,n θj,hj q3,C3,LQ, μ nj,C4,LQ,δ nj,C5,LQ《简明空调设计手册》[18]和《夏热冬暖地区居住建筑节能节标能准设》计[19标]、《准公》共[20建]筑
3.3 蒙特卡罗数值模拟结果
输入项代入Matlab 程序中进行模拟计算。本文设置的模拟次数为2 000 次,从而保障能够得到足够的统计信息。模拟结果见图5 和图6。

图4 办公类建筑照明功率密度分布和随机抽样值Fig.4 Probability distribution sampling value of lighting gain for office buildings
图5 结果表明:区域内6 类建筑仅学校和住宅类建筑的峰值冷负荷服从正态分布。由图6(a)和6(d)可知:区域峰值冷负荷和区域单位建筑面积冷负荷都通过安德森-达令正态性检验,呈正态分布。图6(a)中区域峰值冷负荷均值μ为60 MW,与图5 分类建筑最大概率的峰值冷负荷叠加结果相比降低了10%。
当x 为40~80 MW 时,区域峰值冷负荷的概率密度分布为

当X 为45~90 W/m2时,区域单位建筑面积冷负荷的概率密度分布为

图6(b)中,区域峰值冷负荷在68.3%置信度下为55.4~66.4 MW,均值μ是符合当前节能设计标准的推荐 值, σ 为 正 态 分 布 的 标准 差, (μ ,μ + σ]=(60.9,66.4 ]是常规情景区间, [μ -σ ,μ)=[55.4,60.9)是采用先进技术的低碳情景区间。
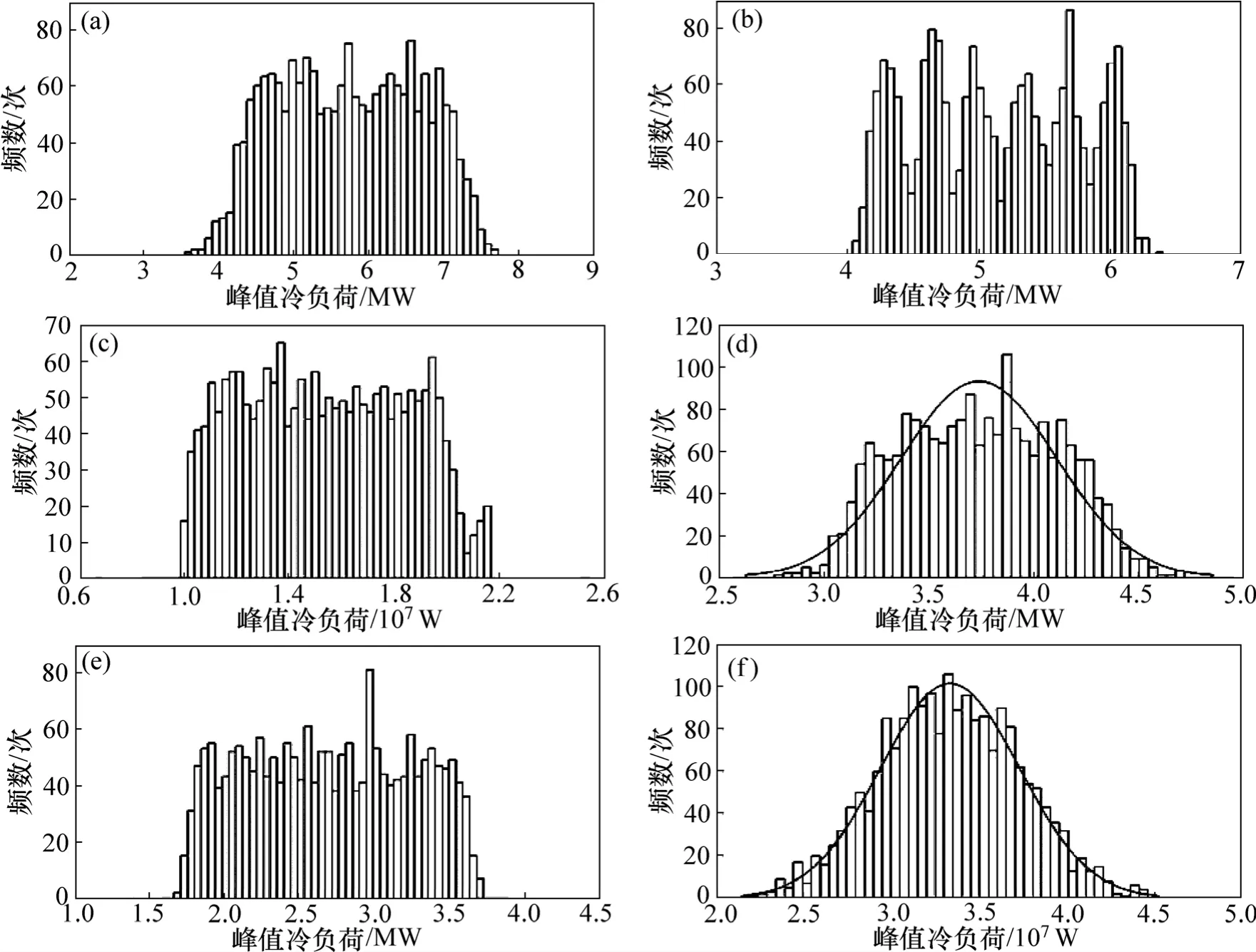
图5 各类建筑峰值冷负荷频数分布Fig.5 Peak cooling load frequency distribution of each type building
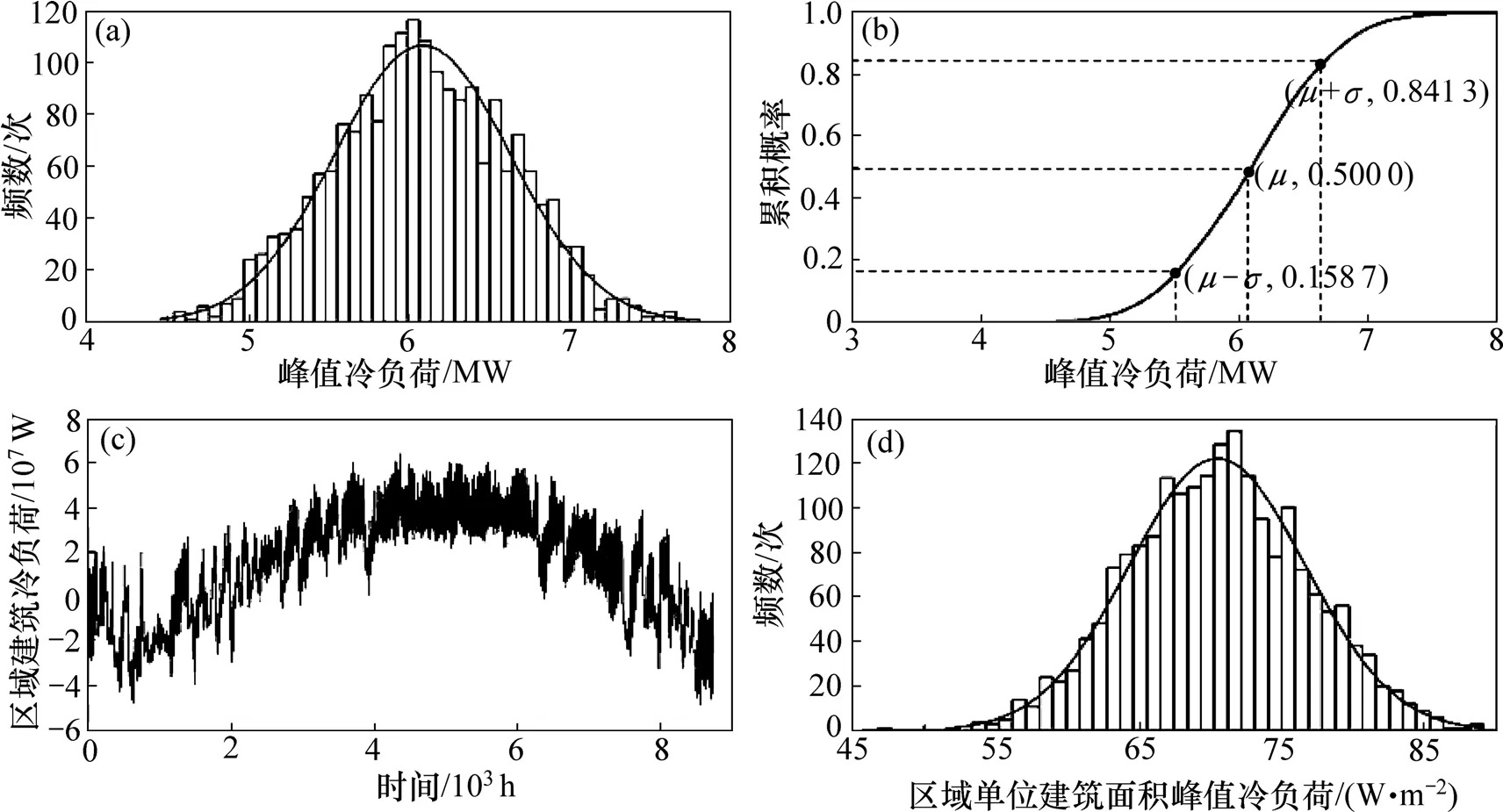
图6 该规划区的冷负荷图Fig.6 Cooling load diagram of study area
4 结论
1) 区域建筑冷负荷预测随机模型解决了区域建筑冷负荷在控制性规划阶段的随机性问题,为区域能源规划提供了新的思路。
2) 确定了随机模型的随机变量分布和随机数的产生方法。
3) 通过随机预测模型得到区域建筑峰值冷负荷的概率分布和累积概率分布,为设计师和决策者提供技术支撑。
4) 提出区域峰值冷负荷推荐值、常规情景区间值和低碳情景区间值预测方法。
5) 在综合考虑随机变量的条件下,得到目标值的概率分布,减少风险投资,提出以区域峰值冷负荷的3 种情景取值,进行系统选型设计,同时还可以降低输送系统能耗,避免系统设备容量选型偏大时导致的设备空置现象。该蒙特卡罗模拟方法简化区域建筑能耗模拟,为下一步进行规划区内电力负荷、燃气负荷、热水负荷预测提供合理的方法支撑。
[1] 王登云, 许文发.低碳城市与建筑区域能源规划[J]. 建设科技,2010(13):68-71.WANG Dengyun, XU Wenfa. Low-carbon city and building energy planning[J]. Construction Science and Technology,2010(13):68-71.
[2] Kavgic M, Mumovic D, Summerfield A, et al. Uncertainty and modeling energy consumption: Sensitivity analysis for a city-scale domestic energy model[J].Energy and Buildings,2013,60:1-11.
[3] Ben-Nakhi A, Mahmoud M A. Cooling load prediction for buildings using general regression neural networks[J]. Energy Conversion and Management,2004,45(13/14):2127-2141.
[4] Papalexopoulos A D,Hao S Y,Peng T M.An implementation of a neural network based load forecasting model for the EMS[J]. IEEE Transactions on Power Systems, 1994, 9(4):1956-1962.
[5] Pagliarini G,Rainieri S.Restoration of the building hourly space heating and cooling loads from the monthly energy consumption[J].Energy and Buildings,2012,49:348-355.
[6] LI Qiong, MENG Qinglin, CAI Jiejin, et al. Applying support vector machine to predict hourly cooling load in the building[J].Applied Energy,2009,86(10):2249-2256.
[7] Lee Y S,Tong L I.Forecasting energy consumption using a grey model improved by incorporating genetic programming[J].Energy Conversion and Management,2011,52(1):147-152.
[8] YAO Ye, LIAN Zhiwei, LIU Shiqing, et al. Hourly cooling load prediction by a combined forecasting model based on analytic hierarchy process[J]. International Journal of Thermal Sciences,2004,43(11):1107-1118.
[9] Dominguez-Munoz F, Cejudo-Lopez J M, Carrillo-Andrs A.Uncertainty in peak cooling load calculations[J]. Energy and buildings,2010,42:1010-1018.
[10] 龙惟定, 白玮, 范蕊, 等. 低碳城市的区域建筑能源规划[M].北京: 中国建筑工业出版社,2011:182-194.LONG Weiding, BAI Wei, FAN Rui, et al. Community energy planning for built environment in low carbon cities[M]. Beijing:China Architecture and Building Press,2011:182-194.
[11] 刘军. 科学计算中的蒙特卡罗策略[M]. 北京: 高等教育出版社,2009:2-15.LIU Jun. Monte Carlo strategies in scientific computing[M].Beijing:Higher Education Press,2009:2-15.
[12] Soratana K, Marriott J. Increasing innovation in home energy efficiency:Monte Carlo simulation of potential improvements[J].Energy and Buildings,2010,42(6):828-833.
[13] Haarhoff J, Mathews E H. A Monte Carlo method for thermal building simulation[J]. Energy and Buildings, 2006, 38(12):1395-1399.
[14] Marmidis G, Lazarou S, Pyrgioti E. Optimal placement of wind turbines in a wind park using Monte Carlo simulation[J].Renewable Energy,2008,33(7):1455-1460.
[15] 曹弋. MATLAB 教程及实训[M]. 北京: 机械工业出版社,2009:150-168.CAO Yi. Training and tutorials of MATLAB[M]. Beijing:China Machine Press,2009:150-168.
[16] LIN Duanmu, WANG Zhenjiang, ZHAI Zhiqiang, et al. A simplified method to predict hourly building cooling load for urban energy planning[J]. Energy and Buildings, 2013, 58:281-291.
[17] 单寄平. 空调负荷实用计算法[M]. 北京: 中国建筑工业出版社,1989:30-71.SHAN Jiping. Cooling load calculation method[M]. Beijing:China Architecture and Building Press,1989:30-71.
[18] 赵荣义. 简明空调设计手册[M]. 北京: 中国建筑工业出版社,1998:26-61.ZHAO Rongyi. Concise handbook of air conditioning system design[M].Beijing:China Architecture and Building Press,1998:26-61.
[19] JGJ 75—2012. 夏热冬暖地区居住建筑节能设计标准[S].JGJ 75—2012. Residential building energy saving standards in hot summer and warm winter area[S].
[20] GB 50189—2005. 公共建筑节能设计标准[S].GB 50189—2005. Design standard for energy efficiency of public buildings[S].
