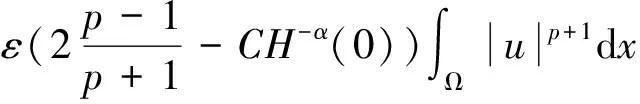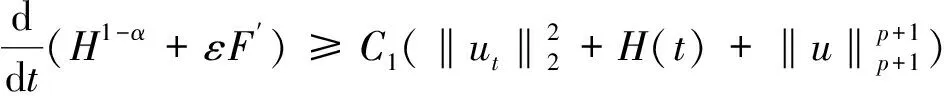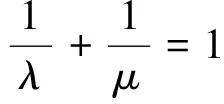具有非线性阻尼及源项的波动方程解的存在性与爆破

李爱萍， 杨慧

(云南师范大学 数学学院，云南 昆明 650500)

1 引言

utt+a|ut|m+1ut-Δu=b|u|p+1u为具有非线性阻尼及源项的波动方程.文献[1-2]中，对a=0时波动方程的Dirichlet初边值问题进行了讨论，并对其解在相应空间的存在性与爆破性作了阐述.对方程的Cauchy问题,文献[3-4]就其能量估计进行了深入讨论.文献[5-6]中对型如utt+δut-φ(x)Δu=λu|u|p-1的非线性波动方程的第一类边值问题解的爆破作了深入讨论.文献[7]中利用能量方法和微分、积分不等式技巧，讨论半线性波动方程具非线性Neumann边界条件的混合问题解的爆破性质.文献[8]中讨论了当a=1、b=1时齐次Dirichlet初边值问题解的存在与爆破问题.本文主要讨论a=1、b=1时，在m和p满足一定条件情况下，如下初边值问题的波动方程解的存在性与爆破：

(1)

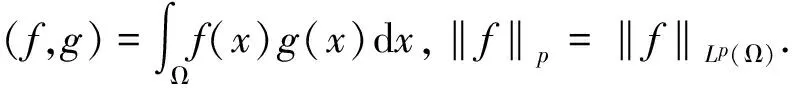
本文的主要结果有：

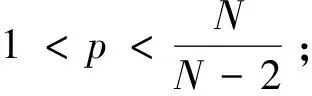
u(t,x)∈L，ut(t,x)∈L(0,T;L2(Ω))∩Lm+1(0,T;Lm+1(Ω)).

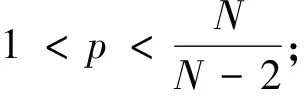
2 定理1的证明

波动方程的形式能量如下：

(2)

首先应用Faedo-Galerkin方法来证明问题(1)弱解的存在性.

(untt,ws)+(un,1≤s≤n

(3)

满足初始条件

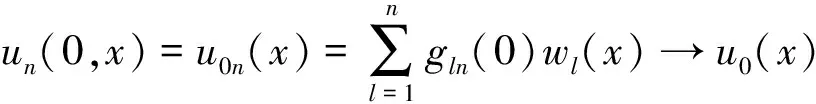
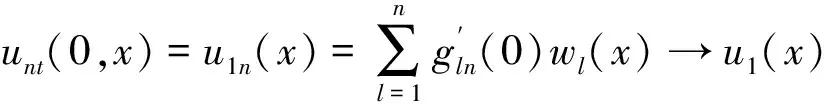
由非线性方程组解的一般结果得方程组(3)的初值问题的解在区间[0,tn]上存在.下面的估计证明了存在与n无关的T，解在区间[0,T]上存在.

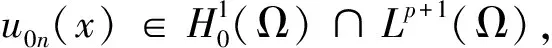
其中

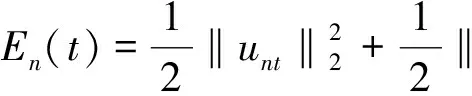
(4)

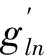
(5)

对上式中的t从0到t积分得

(6)

即

(7)

所以存在与n无关的常数C*使得

(8)

由此得tn=T.

由引理1可知存在{un}的子序列{uv}使得，当v→时，uv→u在L中弱*收敛，且uvt→ut在L(0，T;L2(Ω))中弱*收敛,|uvt|m-1uvt→|ut|m-1ut在Lm+1(0,T;Lm+1(Ω))中弱收敛.

定理1成立.

3 定理2的证明

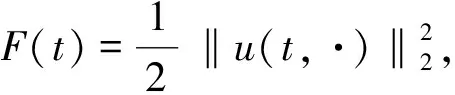
H1-α(t)+εF′(t)

记

(9)

这里ε>0,α>0是小参数，α根据需要适当选取，ε待定.

由能量等式我们得到

(10)

从而H(t)是一个递增函数，注意到条件λQ(u)≤0,所以

(11)

由于

(12)

通过计算得

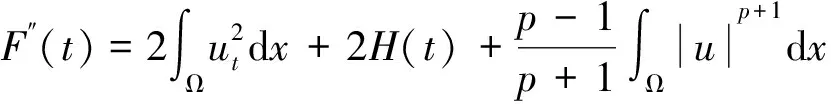
(13)

因此，得到

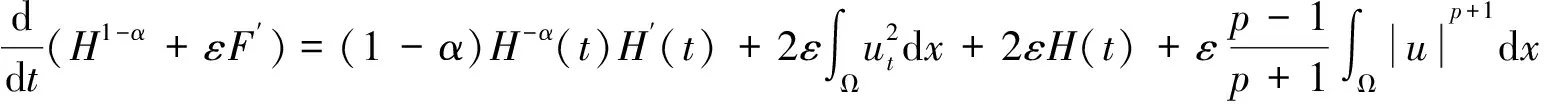
(14)

上式右边项可以通过Hölder不等式并结合m+1

由Young不等式及m+1

其中C、C1>0为常数.

由(10)式,选择适当的α使得

(15)

由定理2 的条件E(0)<0,假设H(0)>1,则有

H-1/(m+1)+1/(p+1)(t)≤H-α(t)≤H-α(0)

因此，我们得到

于是由(14)式并注意到定理2的条件λ[uq(u)-2Q(u)]≤0得到

由(15)式选定α，选取足够小的ε和H(0)足够大，即初值足够大，使得

(16)

从上式我们得到

(17)

(17)式表明H1-α(t)+εF′(t)是一个递增函数.因此选择F′(0)>0,于是对∀t>0得

H1-α(t)+εF′(t)>0

下面我们来证明

(18)

其中C是一个正常数，由(15)式得β=1/(1-α)>1.如果(18)式成立，那么H1-α+εF′在有限时间内爆破，u也在有限时间内爆破.

为了证明(18)式成立，考虑如下两种情况：

(ⅰ)F′(t)≤0.我们有

(H1-α(t)+εF′(t))1/(1-α)≤H(t)，

所以由(11)式和(17)式，得(18)成立.

(ⅱ)F′(t)>0.由Hölder不等式和Young不等式得

由上述不等式及(17)式，得到(18)式，由此定理2得证.

[1] BALL J.Remarks on blow-up and nonexistence theorems for nonlinear evolution equations[J].Quart.J.Math.Oxford,1977,28(2):473-486.

[2] GLASSEY R T.Blow-up theorems for nonlinear wave equation[J].Math.Z.,1973,132:183-203.

[3] HARAUX A,ZUAZUA E.Decay estimates for some semilinear damped hyperbolic problems[J].Achive for Rational Mechanics and Analysis,1988,100(2):191-206.

[4] KOPACKOVA M.Remarks on bounded solutions of a semilinear dissipative hyperbolic equation[J].Comment.Math.Univ.Carolin,1989,30(4):713-719.

[5] LEVINE H.Instability and nonexistence of global solutions to nonlinear wave equations of the formPutt=Au+F(u)[J].Trans.Amer.Math.Soc,1974,192:1-21.

[6] LEVINE H.Some additional remarks on the nonexistence of global solutions to nonlinear wave equation[J].SIAM J.Math.Anal,1974,5(1):138-146.

[7] 田应辉.非线性边界条件下半线性波动方程解的爆破[J].四川师范大学学报:自然科学版,1999,22(5):525-529.

[8] GEORGIEV V,TODOROVA G.Existence of a solution of the wave equation with nonlinear damping and source terms[J].Journal of Differential Equations,1994,109(2):295-308.