单极芒刺静电净化装置芒刺和极板间距对电流密度的影响

桂荔，何源，潘爱强，王灿星*

(1.浙江大学航空航天学院，浙江杭州310027;2.东方汽轮机有限公司，四川德阳618000)

0 引言

高压静电净化设备的电晕极种类有多种，最为常见的为线状电晕放电极。但线-板静电净化装置中存在反电晕现象［1］，离子风与主流叠加会引起二次流或附加湍流［2］，导致净化效率降低。均匀的电流密度分布不仅可以有效地减少流场中大尺度的二次流的产生，利于颗粒的荷电和收集［3］，还可以避免收集板上因局部电荷积累过多而产生的反电晕现象，有利于颗粒的收集［4-5］。与线-板式极配方式相比，芒刺板-板式的电流密度分布更均匀［6］。

电流密度的大小和分布是影响净化效率的重要放电特性。电晕放电极的结构参数中芒刺尖端和收集板的间距、芒刺的间距、芒刺的排布、芒刺长度是电流密度大小及分布的重要影响因素，对净化性能的提高至关重要。单根芒刺的电流密度分布服从t分布［7］，但电晕放电极结构为芒刺板时，放电芒刺受背板和相邻芒刺的影响，在两芒刺之间电流密度急剧衰减，偏离了t分布，因此芒刺要有一定的长度和合适的芒刺间距。向晓东等人［8］确定了芒刺的最优间距为40 mm～60 mm，在此范围内，外加电压和极板间距发生变化时，相邻芒刺的抑制作用很小，放电总电流大，且电流密度分布均匀。芒刺呈正三角形分布时平均电流密度大小和强电流密度都大，电流密度分布比较均匀。McKinney等人［9］定性分析了芒刺板上单根芒刺时芒刺尖端与收集板间距对收集板上电流密度的分布的影响，发现间距小时，电流密度分布与t分布曲线吻合较好，但在背板和相邻芒刺的相互影响下，以及工作电压因素下，间距对电流密度强且分布均匀的定量的优选范围还没有得到。

针对如上状况，本研究采用数值模拟方法对其进行研究。

1 数值模拟方法

1.1 物理模型的建立

为了验证本研究建立的数值模拟方法的可靠性，笔者利用McKinney等人的实验数据加以对比，其单极芒刺板-板静电净化单元装置如图1所示。

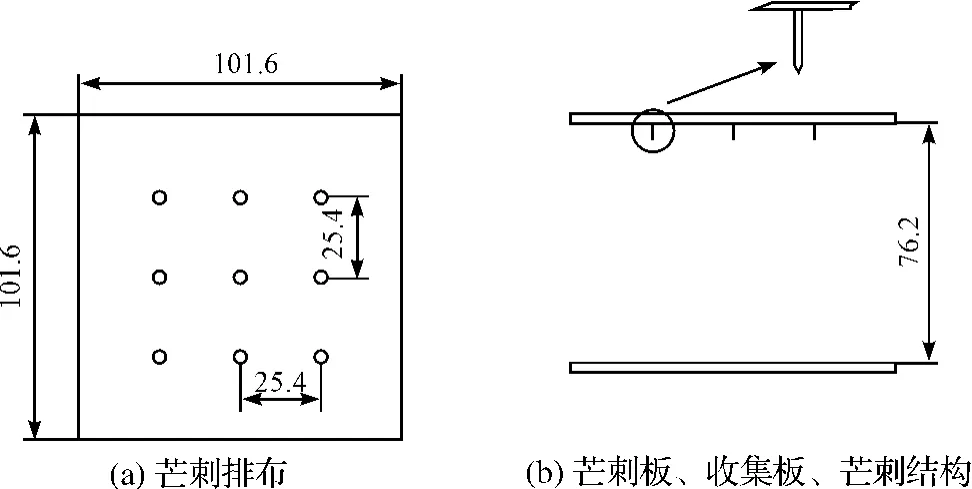
图1 芒刺板-板模型结构图(单位:mm)

上述结构中，极板面积为101.6 mm×101.6 mm，阴极板为3×3根芒刺，芒刺尖端到对面极板距离d=70.7 mm，芒刺的长度L=5.5 mm，芒刺间距s=25.4 mm，芒刺尖端半径r≈0.11 mm，阴极板上的芒刺呈矩阵式分布，行间距和列间距均为25.4 mm。电压为V=50 kV时测得的实验数据为总电流I=97 μA。

1.2 静电场的控制方程

静电场的控制方程为:

式中:Φ—电势，V;E—电场强度，V/m;ρ—空间电荷浓度，C/m2;ε0—真空介电常数，8.854×10-12A/m2。

为了实现数值模拟高压静电场，Alfredo Soldati［10］用直接数值模拟法得出了相应的结果，还有一些学者用有限体积法来离散模拟，都得到了比较好的结果［11］。本研究选用有限体积法，其离散方程格式如下:

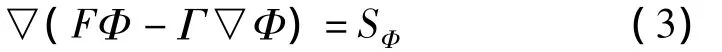
然后利用下式模拟计算电流密度大小及分布:

式中:J—电流密度，A/m2;b—负离子迁移率，2.625×10-4m/s。

1.3 电场的边界条件

芒刺板-板和线-板两种极配方式由于电极结构不同，边界条件也不同，芒刺板-板极配方式的边界条件与线-板式相比更加复杂，在数值模拟中将芒刺尖端近似为半球体，其边界条件如表1所示［12］。具体数值可由Peek方程［13］得到:

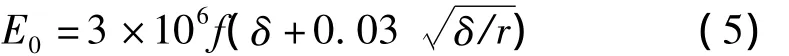
式中:r—芒刺尖端半径，m;f—电晕极粗糙系数，一般为0.6～1;δ—相对空气系数。

且:

式中:T0—标准状态下的绝对温度，273 K;P0—标准状态下的气体压力，1.013×105Pa;T—实际情况下气体绝对温度，K;P—实际情况下的气体压力，Pa。

表1 芒刺板-板静电净化装置的边界条件

1.4 数值模拟结果实验验证

McKinney等人在对9根芒刺矩阵排布的芒刺板电晕放电极的实验中，分析了收集板上电流密度的大小和分布。

电流密度分布的实验结果如图2所示，由图2可以看出，芒刺板状电晕极配方式的收集板的电流密度分布相对均匀，但相邻芒刺对芒刺的电晕放电产生抑制作用，在两芒刺的中间面上，电流密度的急速下降，存在一个“0”区，“0”区内的电流密度值很小。实验数据测得由于相邻芒刺对电晕放电的抑制作用，排布在中心位置的芒刺的放电范围与单根芒刺排布在金属背板上时相比，放电范围由3 cm减小至2.4 cm，但芒刺放电的最大电流密度值不变，近似等于1.91 μA/cm2。

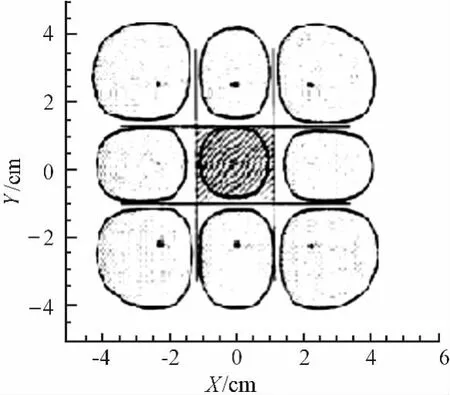
图2 实验测得收集板上电流密度的分布

由数值模拟得出的收集板上电流密度的分布如图3所示，由图3可以看出，中心的芒刺由于周围8根芒刺的放电抑制作用，放电范围为2.5 cm×2.5 cm都小于周围8根芒刺的放电范围。另外收集板上分布在4个角上的芒刺的放电范围最大为2.8 cm×2.75 cm。对比图2可以说明数值模拟结果与实验测得结果大致相同，电流密度分布范围略大。主要原因在于“0”区的电流密度很小，探头的微电流表有一定的精度，此外，数值模拟由简化引起误差。

图3 数值模拟收集板上电流密度的分布

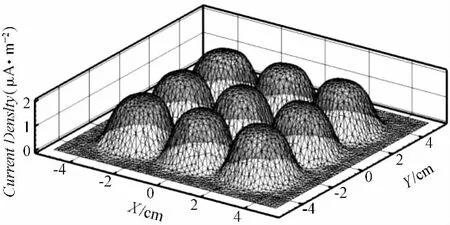
图4 数值模拟收集板上电流密度的大小

数值模拟算得的收集板上电流密度的大小如图4所示，实验测得的收集板电流密度的大小如图5所示。由图4中可以看出9根芒刺的最大电流密度值相同，与图5吻合。且图4中芒刺的最大电流密度值为1.95 μA/cm2，与实验测得的最大电流值1.91 μA/cm2相近。说明本研究采用的数值模拟方法是可靠的。

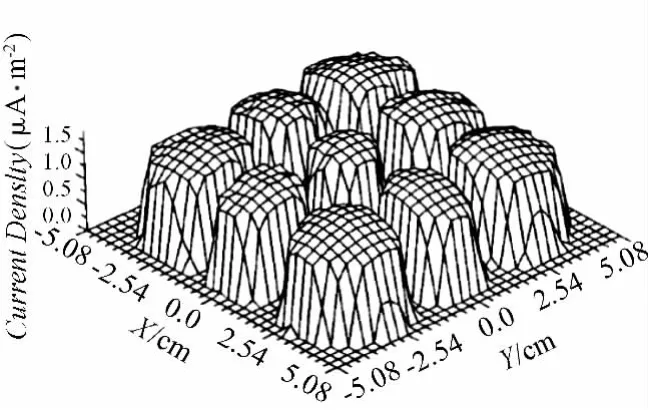
图5 实验测得收集板上电流密度的大小

2 芒刺尖端和收集板间距对电流密度影响分析

芒刺尖端与收集板间距是影响放电特性的重要参数。本研究利用建立的数值模拟方法来研究芒刺尖端与极板间距对电流密度的影响，其装置模型如图6所示。

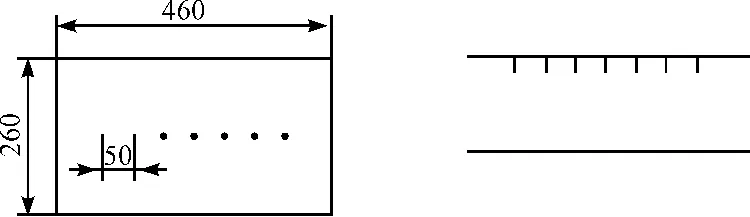
图6 单极芒刺板-板静电净化数值模拟模型(单位:mm)

极板面积为460 mm×230 mm，阴极板为7根芒刺，均布在背板的中心线上，芒刺尖端到对面极板距离可变d=30 mm、40 mm、50 mm、60 mm、75 mm、100 mm、125 mm，芒刺间距选择最优间距范围40 mm～60 mm内的s=50 mm，芒刺的长度L=25 mm，芒刺杆直径D=2.85 mm，锥角为60°，尖端半径r≈0.411 mm。离子的迁移率b=2.3×10-4m/s，T=293 K。

上述模型不同d值的I-V特性曲线如图7所示。图7中，曲线减小d值，在相同的电压下，总电流会增加。通过减小芒刺尖端与收集板间距，空间电荷积聚的空间范围减小，因此对放电的阻碍作用减小，总电流相应会增加，但d过小，击穿电压降低。

图7 不同d值的I-V特性曲线

随后，本研究采用验证过的数值模拟方法模拟了电压V=40 kV时d=30 mm、40 mm、50 mm、60 mm、75 mm、100 mm、125 mm不同间距时的电流密度大小及分布状况，表明不同间距下，随着d值减小，电流密度值增加，但芒刺的放电范围会缩小，且电流密度分布越来越不均匀。结合表2中数据，对于不同间距下电流密度的大小及分布的状况，本研究采用平均电流密度和电流密度几何标准差(两个参数)来定量判断:

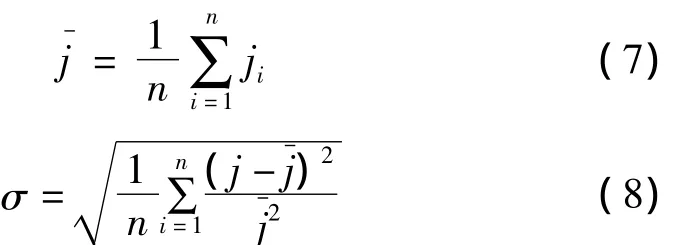
式中:n—n个节点，i—第i个节点。

σ越小表示均匀性越好。从表2中可以看出，d=125 mm时，电流密度分布最均匀，但平均电流密度较小，d=30 mm时平均电流密度值最大，但分布不均匀。收集板电流密度分布均匀是芒刺板-板式极配方式优于线-板式的关键因素，是减少离子风产生的附加湍流和反电晕现象的主要原因。电流密度不均匀时，通常发生反电晕时的电流密度的大小仅相当于理论计算的反电晕发生时的临界电流密度值的1/10，且离子风产生的大尺度二次流容易引起收集颗粒的返混，严重影响净化效率。但电流密度值大时，颗粒的荷电速率也会加快，颗粒达到饱和荷电量的时间缩短，尤其有利于微小颗粒带上更多电荷，在停滞时间内被收集［14］，进而提高总的净化效率。因此，在保证电流密度均匀性的前提下，提高电流密度的大小也同样重要，因此芒刺尖端与收集板之间存在一个最优的间距，在这个间距范围内，电流密度强且分布均匀。

针对单极芒刺板-板式静电净化装置，在结构参数一定时，影响收集板电流密度大小的重要因素是工作电压。性能好的电晕放电极要求起晕电压低，击穿电压高。电场的均匀度对击穿电压有着显著影响，因此放电间隙d越大击穿电压会越高。极不均匀尖-板击穿电压与放电间隙的关系图如图8所示［15］，当放电间隙d=30 mm时，击穿电压小于60 kV，电压工作范围较小。

图8 尖-板空气间隙的直流击穿电压

d=50 mm时，在小于击穿电压的范围内调整电压值从40 kV增加到60 kV时，平均电流密度和电流密度几何标准差的值如表3所示，可以看出电压从40 kV增加到60 kV时，平均电流密度值增加了125%，增幅明显，而电流密度分布的均匀性几乎不受影响，而且由图8可以看出d=50 mm时，击穿电压近似为100 kV，因此电流密度的值可以在分布均匀的情况下有较大空间的提升。

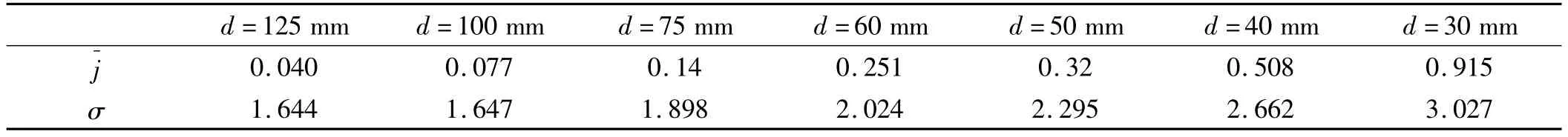
表2 不同d值下，平均电流密度和电流密度几何标准差

表3 不同电压时的平均电流密度和电流密度几何标准差

综合考虑电流密度值的大小和分布情况，本研究提出了芒刺尖端和收集板的合理范围为40 mm～75 mm的范围内，在这个范围内，单极芒刺板-板净化装置的击穿电压高因此工作范围广，且在保证电流密度分布均匀的情况下，电流密度值可以很强。

3 结束语

本研究采用描述电场分布特性的泊松方程和电流连续性方程，将芒刺尖端近似为半球状，并根据线-板极配方式改进边界条件，给出了较为准确的芒刺板状电晕的数值模拟方法，并结合McKinney关于芒刺板电流密度实验结果来验证数值模拟方法的可靠性。数值结果与实验值相比略偏大，这是因为模拟过程中的间化处理，但能很好地捕捉到电流密度大小和分布的规律。

笔者利用建立的可靠的数值模拟方法对芒刺板状电晕极配方式的结构参数中的芒刺尖端与极板间距对电流密度的影响进行研究，得出结论:对于单极芒刺板-板静电净化装置，增大芒刺尖端与收集板的间距，收集板上电流密度分布更加均匀但电流密度值减小。减小芒刺尖端与收集板的间距，在相同工作电压下，总电流会相应增大，收集板上平均电密度值增大，但分布均匀性受影响。收集板电流密度分布均匀是芒刺板-板式极配方式优于线-板式的关键因素，是减少离子风

产生的附加湍流和反电晕现象的主要原因。电流密度不均匀时，反电晕和离子风产生的大尺度二次流严重影响净化效率。但电流密度值大时，颗粒的荷电速率也会加快，有利于微小颗粒带上更多的电荷，在停滞时间内被收集，进而提高总的净化效率。因此，在保证电流密度均匀性的前提下，提高电流密度的大小也同样重要。芒刺尖端与收集板之间存在一个最优的间距范围，在这个间距范围内，电流密度强且分布均匀。随后笔者利用所建立的可靠的数值模拟方法又对工作电压对电流密度的影响进行研究，得出结论:增加工作电压可以相应地提高电流密度值但对电流密度分布均匀性的影响不大。因此在合适的间距范围内，可以通过增强工作电压得到更强的电流密度值，并且电流密度分布均匀性不受影响。本研究在工作电压的影响下，综合考虑电流密度值的大小和分布情况，本研究提出了芒刺尖端和收集板的合理范围为40 mm～75 mm，在这个范围内，单极芒刺板-板净化装置的击穿电压高因此工作范围广，则可以在保证收集板上电流密度分布均匀的情况下，在高工作电压下得到强的电流密度。

［1］JAWOREK A，CZECH T，RAJCH E，et al.Laboratory studies of back-discharge in flyash［J］.Journal of Electrostatics，2006，64(5):326-337.

［2］LARSEN P S，SÖRENSEN S K.Effect of secondary flows and turbulence on electrostatic precipitator efficiency［J］.Atmospheric Environment，1984，18(10):1963-1967.

［3］DAVIDSON J H，MCKINNEY P J.Electrohydrodynamic precipitator flow with a barbed plate discharge electrode［J］.Aerosol Science and Technology，1990，12(2):319-334.

［4］向晓东，邹霖.电收尘极板上沉积尘的附着力与振打加速度［J］.安全与环境学报，2006，6(1):112-115.

［5］JAWOREK A，CZECH T，RAJCH E，et al.Laboratory studies of back-discharge in fly ash［J］.Journal of electrostatics，2006，64(5):326-337.

［6］MCKINNEY P J，DAVIDSON J H.Comparison of electrical characteristics of barbed-plate and wire-plate precipitators［C］//IndustryApplicationsSocietyAnnualMeeting，1993.，Toronto:［s.n.］，1993:1864-1869.

［7］SIGMOND R S.Simple approximate treatment of unipolar space-charge dowinated coronas:The warburg law and the saturation curret［J］.Journal of Applied Physics，1982，53(2):891-898.

［8］郭尹亮，向晓东，盖龄童.芒刺电除尘器板电流密度分布及芒刺间距优化［J］.高电压技术，2010，36(4):1021-1025.

［9］MCKINNEY P J，DAVIDSON J H，LEONE D M.Current distributions for barbed plate-to-plane coronas［J］.IEEE Transactions on Industry Applications，1992，28(6):1424-1431.

［10］SOLDATI A.On the effects of electrohydrodynamic flows and turbulence on aerosol transport and collection in wireplate electrostatic precipitators［J］.Journal of Aerosol Science，2000，31(3):293-305.

［11］LONG Zheng-wei，YAO Qiang，SONG Qiang，et al.A second-order accurate finite volume method for the computation of electrical conditions inside a wire-plate electrostatic precipitator on unstructured meshes［J］.Journal of E-lectrostatics，2009(67):597-604.

［12］DAVIDSON J H，MCKINNEY P J，LINNEBUR P.Threedimensional(3-D)model of electric field and space charge in the barbed plate-to-plate precipitator［J］.Industry Applications，IEEE Transactions on，1996，32(4):858-866.

［13］PEEK F W.Dielectric Phenomena in High Voltage Engineering［M］.McGraw-Hill Book Company，Incorporated，1920.

［14］小奥格尔斯比，尼克尔斯.电除尘器［M］.谭天佑，王励前，译.北京:水利电力出版社，1983.

［15］周泽存.高电压技术［M］.北京:中国电力出版社，2004.