飞机垂尾抖振响应的飞行试验研究
2014-03-29李小路
李小路, 唐 凯, 雷 鸣
(中国飞行试验研究院, 西安 710089)
0 引 言
现代空战形式的发展对作战飞机的机动性能提出了越来越高的要求,以F/A-18等战斗机为代表的现代高性能战斗机应运而生。这些现役的主流战斗机为了适应现代空战的需求,其飞行包线已经扩展到有气流分离、脱体涡、涡破裂等现象发生的大迎角范围。为提高和改善大迎角飞行性能,现代战斗机常采用前缘襟翼、边条翼、鸭翼等,以提供一定的涡升力,而且当这些分离涡带着气流掠过垂尾时还可以维持飞机的稳定性。但是,在有些情况下这些分离涡在到达垂尾前就发生破裂,从而形成高度紊乱、旋转的非定常尾涡流。这种涡流在一定的频率带宽内具有集中显著的能量,如果这种尾涡流所具有的频带范围覆盖了垂尾结构的某一阶或几阶模态的固有频率,涡流作用在垂尾结构上将会诱发严重的垂尾抖振现象。图1是NASA的研究人员在F/A-18飞行中利用烟雾法进行涡流破裂现象演示试验的两张照片。

(a) 20°迎角 (b) 30°迎角
这些来自机翼和机身前缘的非定常尾涡流打在处于其后方的垂尾上,会导致非常大的抖振力作用于垂尾结构的主要承力部件上,会对结构的疲劳寿命产生非常显著的不利影响。实践证明,这种高度紊乱、旋转的非定常尾涡流,对双垂尾布局的战斗机(如F-35、F-22、F/A-18)的垂尾结构是极为有害的[1-2]。这些高性能双垂尾战斗机在服役不久,就发现在数次大迎角飞行后,垂尾产生了疲劳裂纹,究其原因是由垂尾抖振引起的[3]。随之而来的是巨额的垂尾维修、更换费用,美国军方仅对F-15飞机由于疲劳损伤所导致的垂尾维修和更换所耗费的费用大约为每年600万美元[4]。F-22、F-35也在试飞早期出现了因为垂尾抖振引起的结构疲劳破坏问题。所以,双垂尾飞机的抖振问题一直是当今美国飞行试验的核心。
F-22试验团队为解决因为抖振引起的大的方向舵激励载荷问题,通过机体上加装的振动加速度传感器和载荷应变,在跨声速和亚声速范围内开展了一系列以收敛转弯和破S机动在内的抖振试飞工作。通过试验发现产生大响应的抖振激励模态在30~60Hz之间,在马赫数0.5时,以30Hz作为主要的抖振响应频率;在马赫数0.8~0.9时主要响应频率范围则变为50~60Hz;且抖振响应随空速、动压和迎角的增加而增加[1,5-6]。
F-18在早期的试飞过程中,也发现飞机在大迎角下,从LEX上脱落的涡流与机身后部发生撞击而产生严重的抖振问题。为解决此问题,试验人员在垂尾上加装了脉动压力传感器和振动加速度传感器。试验在一个较宽的飞行包线范围内一共完成了包括收敛转弯、破S机动以及平飞加减速等飞行机动共计309次,给出了飞行试验和风洞试验过程中测得的压力和加速度自功率谱密度数据的对比结果,试验发现实际飞行中的抖振载荷要明显比先前预测的数据大,抖振响应模态主要为第一弯曲和第二弯曲模态,且最大响应出现在30°迎角附近[7-8]。
F-15的双垂尾抖振则是由机翼分离流尾迹作用在其表面的脉动载荷引起,试验发现其尾迹的脉动载荷带宽很窄但包含了垂尾的一阶扭转频率,从而使垂尾抖振响应主要表现为一扭模态,并在迎角22°左右达到最大值[4]。
我国的西工大低速风洞实验室及中国空气动力研究与发展中心都对垂尾抖振产生的机理做了大量的风洞试验,分别通过在半刚性垂尾模型上加装加速度传感器、脉动压力传感器以及应变片,对在低速大迎角下,F-18、F-22的垂尾抖振情况进行了的风洞试验模拟,并就垂尾的不同结构、不同位置对抖振的影响进行了研究[9-11]。在上世纪90年代国内曾进行过歼击机的抖振风洞和飞行相关性方面的工作,并通过飞机上的翼尖加速度和翼根弯矩数据对歼击机抖振边界进行了试飞研究,对包括平飞拉起、稳定盘旋、收敛转弯在内的各种抖振机动进行了对比分析,并通过建立均方根、功率谱密度与迎角的关系曲线得到了飞机的初始抖振边界[12-15]。但对飞机在实际飞行中垂尾的抖振情况尚未展开相关的研究工作。为了研究飞机垂尾在飞行中的抖振变化规律,通过在飞机上加装相关测试设备,对其飞行方法、机动动作过程中垂尾的响应以及抖振初始迎角的确定等工作做了相关研究。
1 抖振飞行方法的选择
为了能够准确得到飞机在飞行过程中的抖振响应数据,就必须选择合适的飞行方法,由于飞机在做稳定水平飞行时,有:
式中:L为飞机的升力,W为飞机的重量,CL为升力系数,q为动压,S为飞机翼展面积,ρ为大气密度,M为马赫数,c0为标准大气压下声速。
对于更为普遍的非稳定飞行情况,引入过载n:
n=L/W
则可得到更为普遍的公式:
由于飞机翼展面积S和标准大气压下声速c0是已知量,式中的变量包括过载系数n,飞行马赫数M,与迎角有关的升力系数CL,以及与高度、大气环境有关的系数ρ[16]。
由于在接近等高度的情况下,ρ的变化很小,可以假定ρ为定值,为了能更好的分析飞机抖振响应随飞行参数变化的规律,可以让n、M、CL3个变量中的一个为定值,即可得出另两个参数间的关系曲线,从而得到飞机在实际飞行中的抖振响应情况。
所以,抖振飞行在选择机动动作时,一般可以根据以下3种原则来选取:
(a) 保持马赫数M不变,改变载荷因子n和升力系数CL(如收敛转弯、破S机动等);
(b) 保持载荷因子n不变,改变马赫数M和升力系数CL(如平飞加减速);
(c) 保持升力系数CL不变,改变载荷因子n和马赫数M(如固定迎角的减速机动)。
此次抖振飞行采用的收敛转弯机动,即是在保持高度(即ρ)和马赫数M基本不变的情况下,逐步增大飞机迎角(即升力系数CL),以得到该马赫数下的抖振响应[8]。
2 抖振飞行试验
为了研究实际飞行过程中飞机垂尾的抖振情况,在飞机垂尾上加装了6个振动加速度传感器,分别位于左、右垂尾翼尖前缘、后缘以及垂尾中部前缘附近刚度相对较高的结构上。具体位置如图2所示(左、右垂尾上振动传感器位置一致)。
飞行选取的气压高度都在10km,按规定的马赫数(马赫数分别选取0.65、0.7、0.75、0.8、0.85、0.9和0.95)稳定平飞开始进入收敛转弯机动。
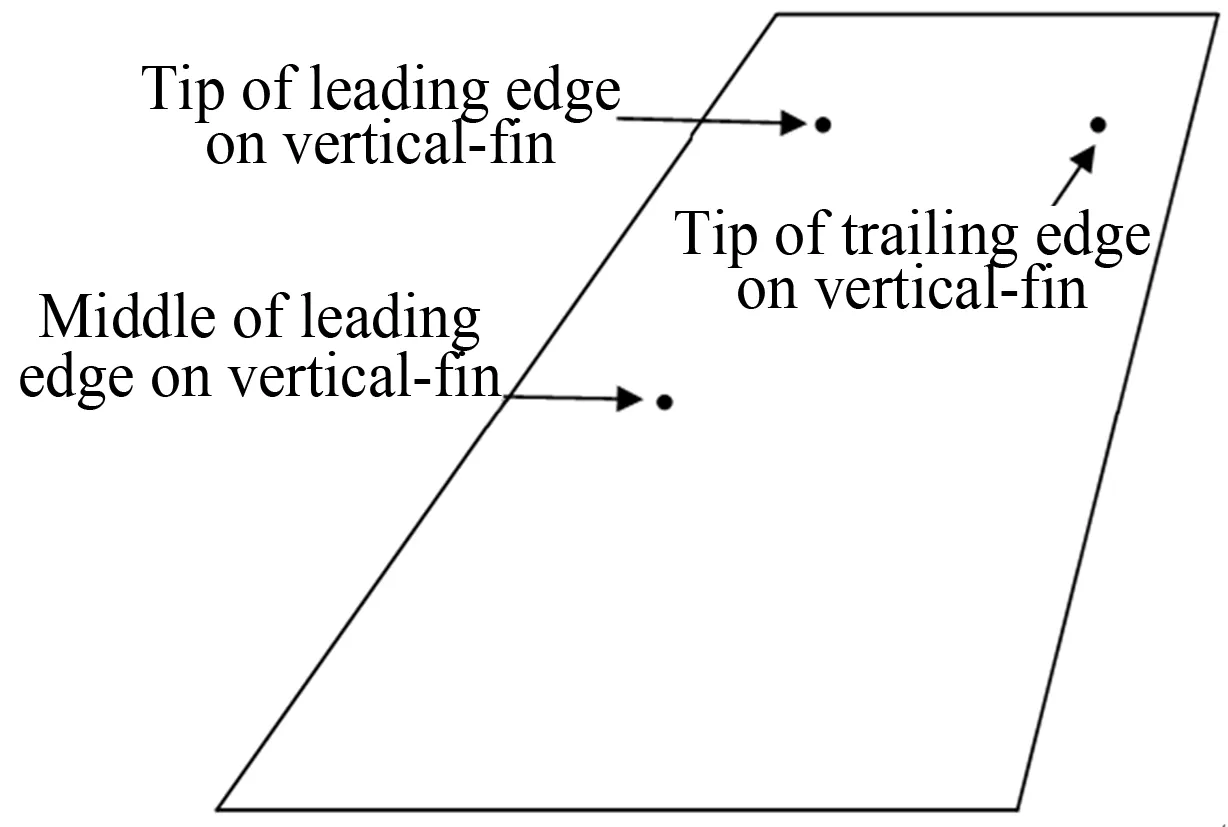
图2 垂尾上振动加速度传感器位置示意图
2.1垂尾振动加速度均方根值随迎角的变化曲线
图3和4分别给出了飞机在气压高度10km,马赫数0.65和0.85进行收敛转弯的过程中,垂尾上各点振动加速度时域均方根值随迎角的变化曲线。从图中可以看出,振动加速度响应均方根值在垂尾翼尖后缘处大于垂尾翼尖前缘处,而垂尾翼尖中部位置的响应最小。
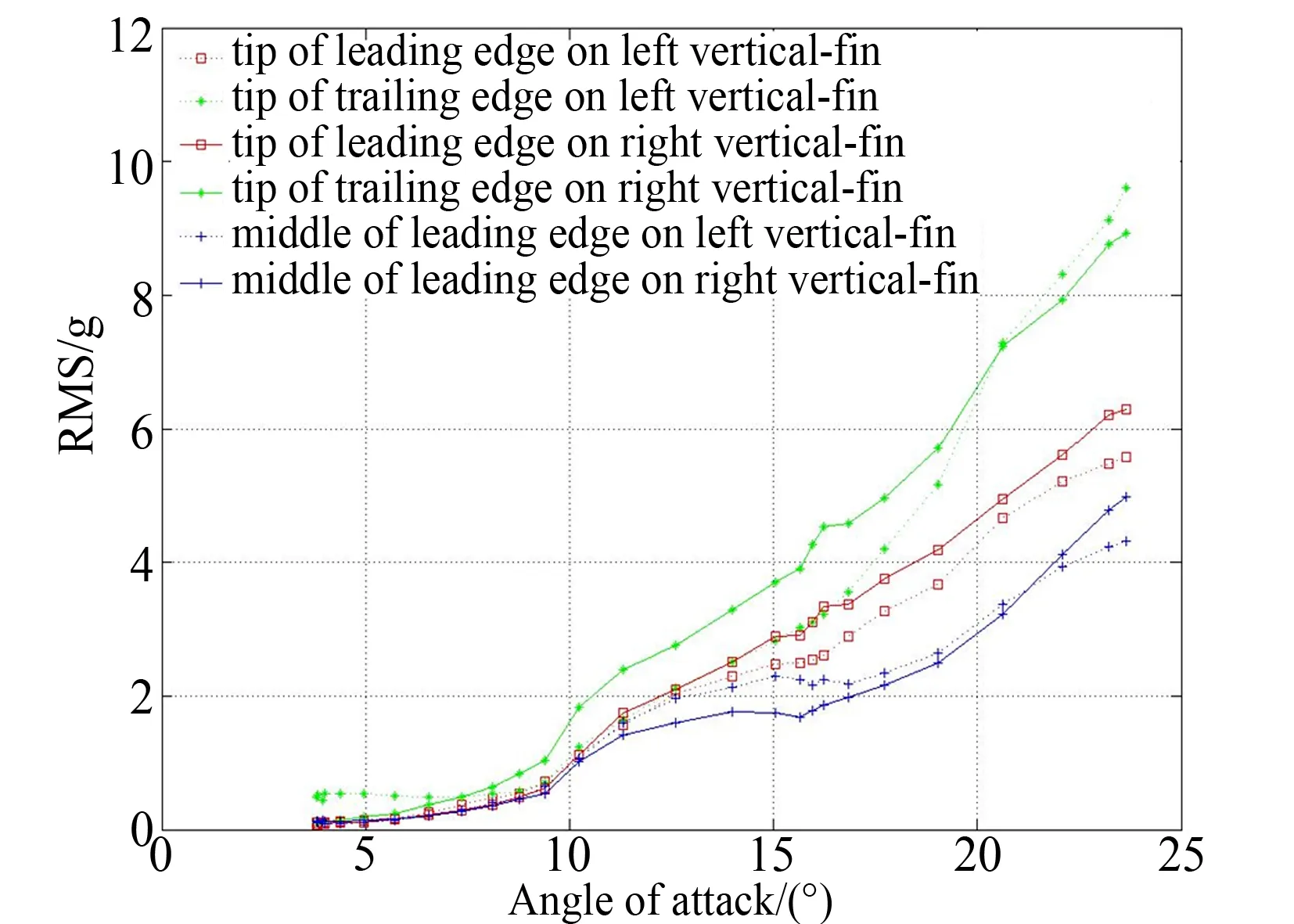
图3 气压高度10km、马赫数0.65时,垂尾各点振动加速度均方根值随迎角的变化曲线
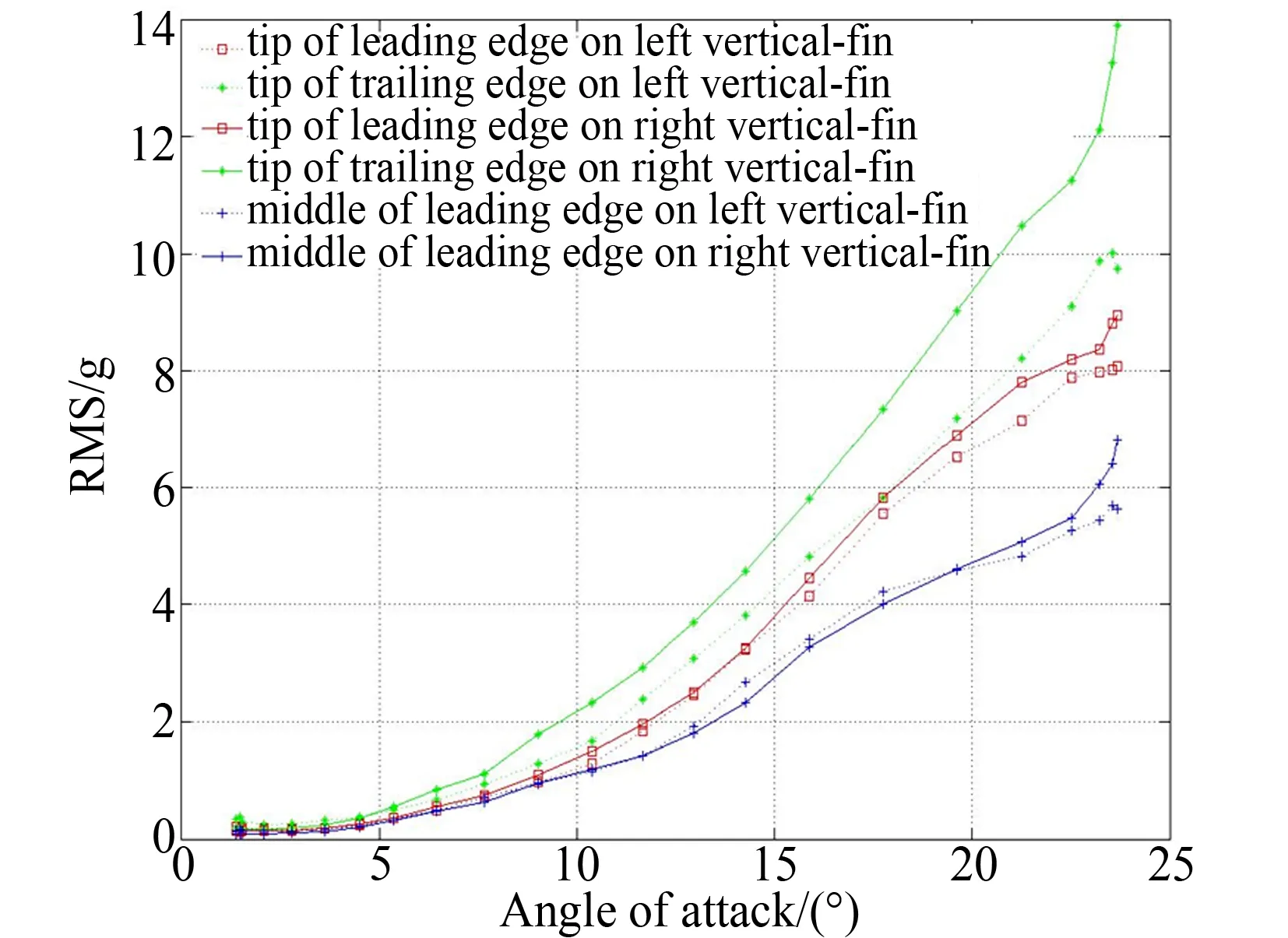
图4 气压高度10km、马赫数0.85时,垂尾各点振动加速度均方根值随迎角的变化曲线
左、右垂尾上各点的振动响应随迎角的变化趋势基本一致,随迎角的增大,垂尾后缘处响应的增长明显大于垂尾前缘处,这可能与机翼前缘边条翼脱落涡随迎角的增大以及破裂点逐渐后移有关。
马赫数0.85时垂尾上各点的振动响应在相同迎角的情况下均较马赫数0.65时要大,说明了抖振的峰值响应随马赫数的增加而增加。
在垂尾翼尖处,右垂尾响应较左垂尾略大。这可能是由于测滑角的影响或在做机动动作过程中试验环境不对称导致的。
2.2垂尾振动加速度时频分析
为了观察在整个收敛转弯过程中各点振动加速度响应在频域上的变化趋势,通过对数据滤波后进行的时频分析,给出了垂尾上各点振动加速度的时频分析结果。图5由上到下依次是收敛转弯过程中马赫数、气压高度、迎角随时间的变化曲线(a)以及垂尾翼尖前缘(b)、垂尾翼尖后缘(c)、垂尾翼尖中部(d)的时频分析图(颜色越亮表示该时刻对应的频率响应越大)。
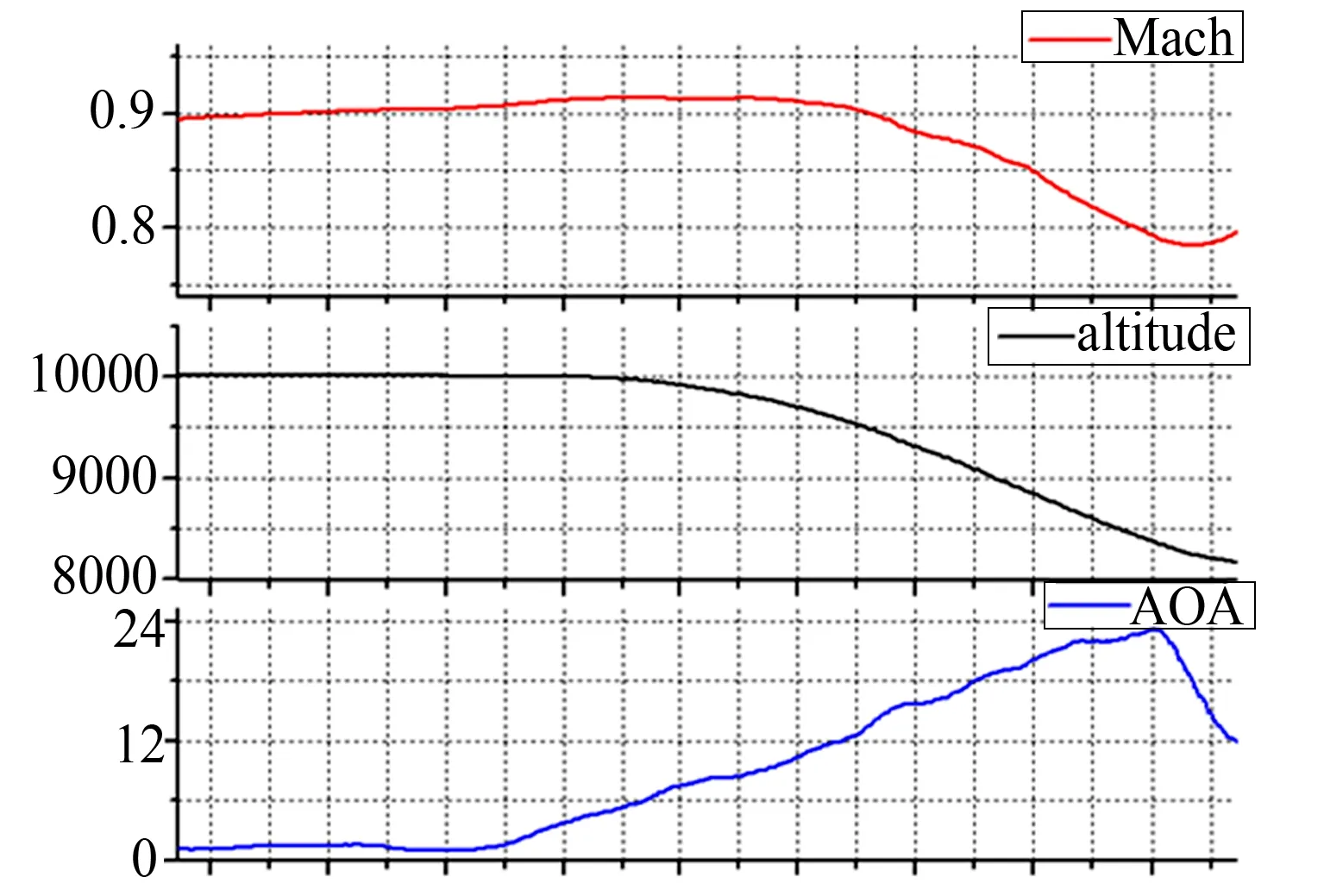
(a)
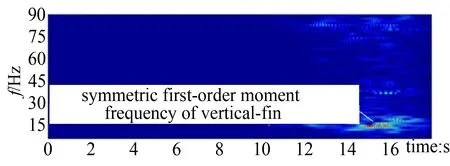
(b) Time-frequency analyses for tip of leading edge on vertical-fin
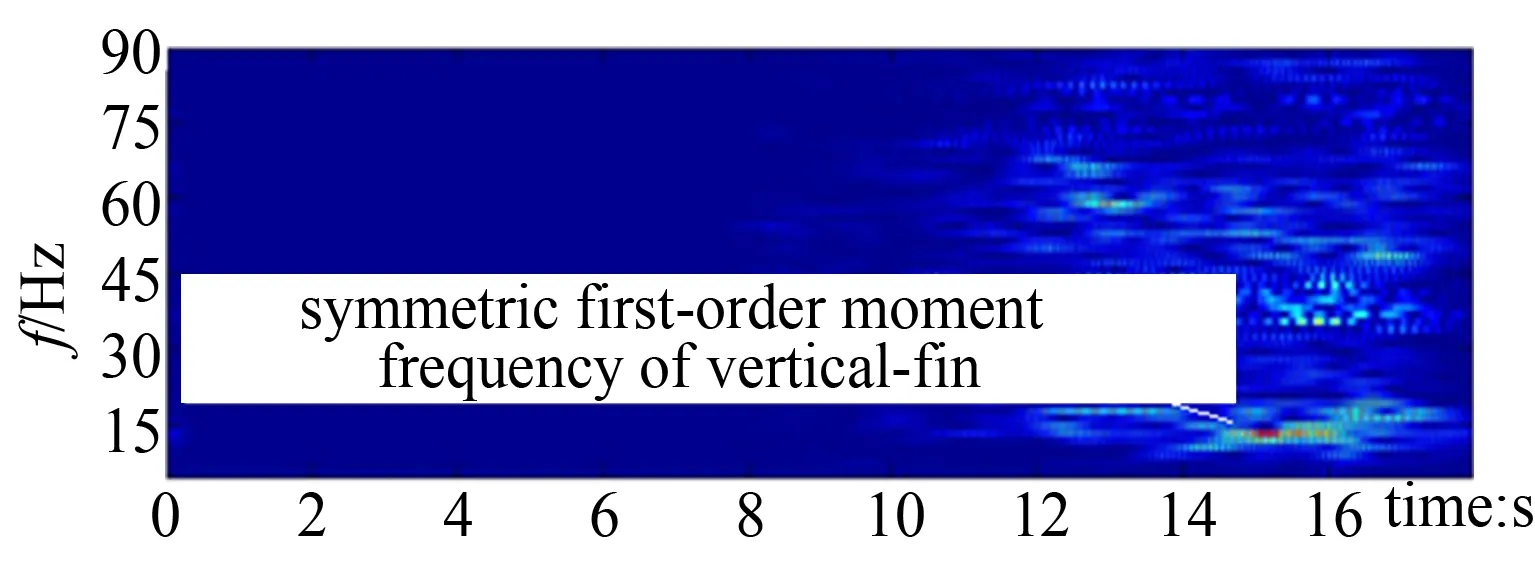
(c) Time-frequency analyses for trailing of trailing edge on vertical-fin

(d) Time-frequency analyses for middle of trailing edge on vertical-fin
从图中可以看出,当迎角大于12°时,飞机随着迎角的增大,在整个频域范围内的振动响应都有所增强;而当迎角大于19°时,垂尾上各点的振动响应主要表现在13.5和39Hz左右对应的频率点上。上述两个频率点恰好在飞机垂尾的对称一弯(12.9Hz)和对称一扭(38.4Hz)模态附近。这与飞机的升力型抖振的特点是吻合的,说明飞机垂尾在迎角超过19°以后确实受到了飞机机翼脱落涡破裂的影响而发生抖振,而且破裂涡的能量主要集中在低频上,该频带范围包含了垂尾一弯和一扭模态频率。
由于受垂尾模态振型的影响,垂尾上不同位置的振动响应有所区别。在抖振发生时,垂尾翼尖处的振动,以13.5Hz左右的频率为主;而在垂尾中部的振动,主导频率则为39Hz。从图上还可以看出,在整个收敛转弯过程中,39Hz左右的频率首先被激发出来,其次才是13.5Hz。这与表征涡流特征的Strouhal公式反映的变化规律一致:
Strouhal=fc/U
式中:Strouhal数与流体流动状态的雷诺数有关,在机动过程中,可认为该值基本不变。 所以,从公式看出,在迎角增加(机翼特征长度c变大)、马赫数减小(自由流的来流速度U值减小)的过程中,要保持Strouhal数不变,漩涡频率f必然减小。
2.3抖振初始迎角分析
抖振初始迎角是判断飞机是否进入抖振的标志,从以往国内外资料来看,抖振初始迎角往往是通过时域或半功率谱密度的均方根值随迎角的变化曲线进行确定,但由于飞机在空中机动飞行过程中姿态难以保持,且受紊流及气动刚度的影响,用上述方法往往存在困难。为了更准确地进行判断,在分析时利用了时频分析方法,该方法可以很直观的反映振动响应在时域和频域上的变化规律。图5中,垂尾的振动响应主要集中在垂尾一弯和一扭频率上,但因为一扭模态频率相对较高,在抖振发生时,以一弯模态对垂尾的影响最为显著,所以在确定抖振初始迎角时,以垂尾一弯模态(13.5Hz)响应的变化情况进行判定。从图中可以看出,在该频率点上响应显著增加时对应的马赫数和迎角分别是0.86和19°。据此可以认为,在气压高度10km、马赫数0.86时的初始迎角为19°。同样的,对其他状态下的数据进行分析后,给出了该机型在气压高度10km左右,不同马赫数对应的抖振初始迎角,如表1所示。

表1 不同马赫数下对应的抖振起始迎角
2.4自功率谱密度分析
为了比较飞机在不同状态下垂尾抖振的响应情况,对垂尾翼尖前缘位置在每个收敛转弯机动过程中,最大抖振响应时的振动加速度响应情况进行了功率谱密度分析。各机动过程中,最大抖振响应时对应的马赫数及其迎角值如表2所示:

表2 每个收敛转弯机动过程中,最大抖振响应时对应的马赫数和迎角值
图6给出了在迎角28°左右,不同马赫数下(马赫数分别为0.58、0.63、0.68和0.71)垂尾翼尖前缘处振动响应的功率谱密度曲线。可以看出,所有状态下垂尾翼尖前缘处的能量都主要集中在12.5Hz(即垂尾的对称一弯模态频率)左右。其中,最大响应出现在马赫数0.71、迎角27°的时候,在12Hz的频率点上功率谱密度值达到11.20g2/Hz。在迎角基本相同的情况下,垂尾峰值频率处的抖振响应同马赫数成正比,抖振峰值频率由于受气动刚度的影响随马赫数的增加略有减小。
图7给出了不同状态下(3种状态分别为马赫数0.71、迎角27°,马赫数0.81、迎角23°,马赫数0.91、迎角16°),垂尾翼尖前缘处振动响应的功率谱密度曲线。从图中可以看到,随着马赫数的增大,由于受最大响应时抖振迎角减小的影响,抖振响应明显减小。
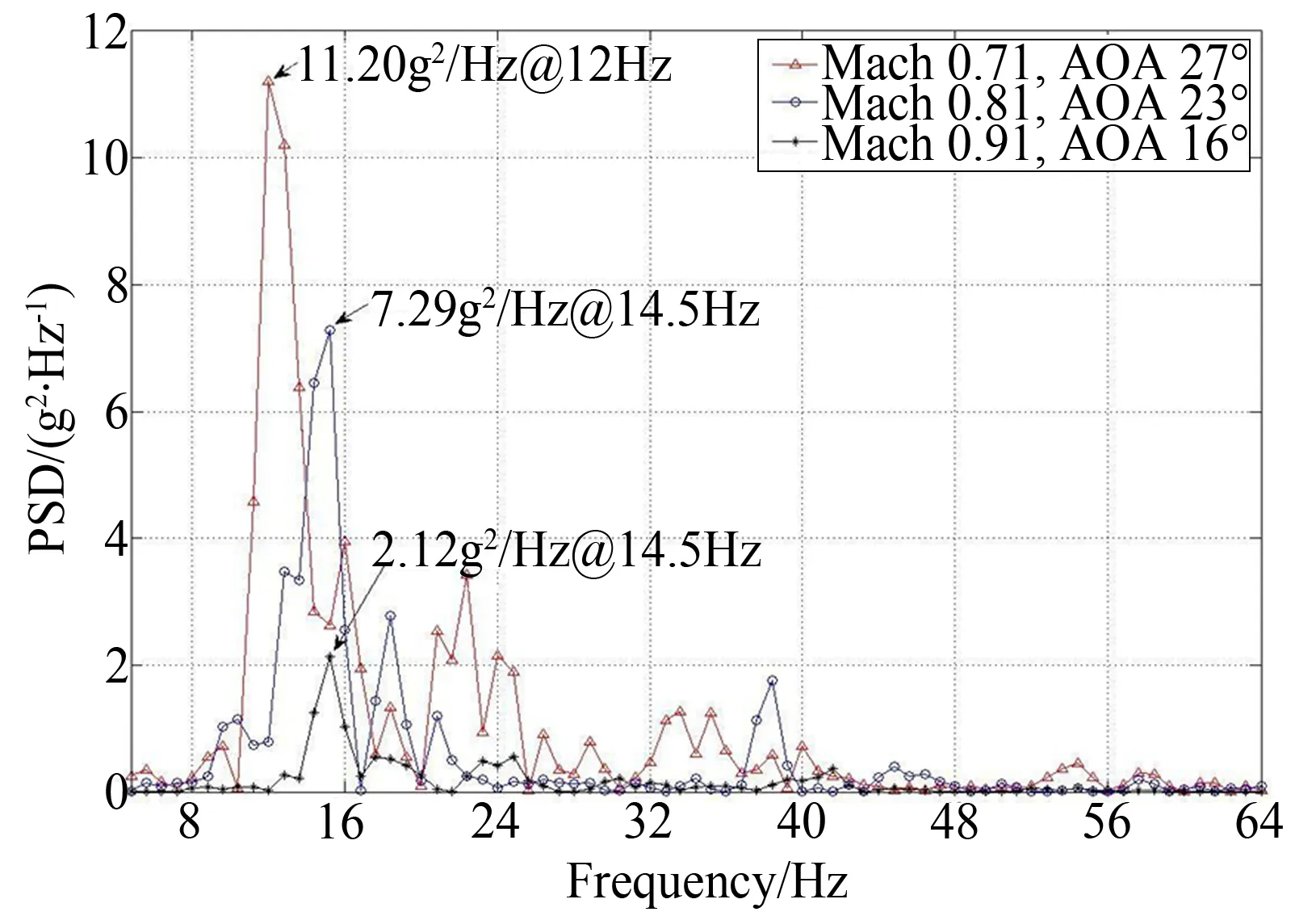
图7 垂尾翼尖前缘振动加速度在不同的马赫数和迎角状态下的功率谱密度曲线
由此可以发现,飞机垂尾的最大抖振响应受迎角的影响最为突出。在一定的马赫数范围内,由于垂尾最大抖振响应时对应的迎角变化不大,在此过程中,垂尾抖振的峰值响应随马赫数的增加而增加;但随着马赫数的继续增加,飞机迎角受抖振迎角的限制而急剧减小,导致垂尾抖振的峰值响应也显著降低。
3 结 论
就飞机抖振试验中可以采用的飞行方法进行了分析;并通过在飞机垂尾上加装振动加速度传感器,对飞机在飞行过程中垂尾的抖振响应情况进行了研究,试验结果发现:
(1) 垂尾的抖振响应主要集中在垂尾的一弯模态和一扭模态频率附近,垂尾在不同模态频率下的响应大小同马赫数、迎角以及测点位置有关;
(2) 通过结合时频分析中一弯模态频率处响应的变化情况给出了各马赫数下飞机的抖振初始迎角,抖振初始迎角随马赫数的增加而减小;
(3) 由于受脱落涡破裂点位置的影响,随迎角的增加,垂尾翼尖后缘处的抖振响应明显大于垂尾翼尖前缘位置;
(4) 在高度基本相同的情况下,垂尾的抖振响应受迎角的影响大于受马赫数的影响,垂尾抖振响应均随迎角和马赫数的增加而增加。
参考文献:
[1]William D Anderson. F/A-22 high angle of attack buffet-test adequacy analysis[R]. AIAA 2004-5084, 2004.
[2]Robert W Moses. Spatial characteristics of F-18 vertical tail buffet pressures measured in flight[R]. AIAA 98-1956, 1998.
[3]Hanagud S. Tail buffet alleviation of high performance twin tail aircraft using piezo-stack actuators [R]. AIAA 99-1320, 1999.
[4]Hanagud S. F-15 tail buffet alleviation: A smart structure approach[R]. Georgia Institute of Technology, 1996.
[5]Suresh R. Patel. Statistical modeling of F/A-22 flight test buffet data for probabilistic analysis[R]. AIAA 2005-2289, 2005.
[6]Suresh R. Patel. F/A-22 Vertiacl buffet strength certification[R]. AIAA 2005-2292, 2005.
[7]Scott A Morton. High resolution turbulence treatment of FA-18 tail buffet[R]. AIAA 2004-1676, 2004.
[8]Healey M D. F/A-18 EF vertical tail buffet design, analysis and test[R]. AIAA 2003-1886, 2003.
[9]李劲杰, 杨青, 杨永年, 等. 边条翼布局双垂尾抖振特性与机理风洞实验研究[J]. 空气动力学学报, 2006, 24(4): 397-402.
Li Jinjie, Yang Qing, Yang Yongnian, et al. The wind-tunnel investigation of the characteristica and mechanism of twin-vertical tail buffet of leading-edge extension configuration[J]. Acta Aerody Namica Sinica, 2006, 24(4): 397-402.
[10] 杨永年, 杨青, 肖春生, 等. 边条翼布局流场及其双垂尾抖振特性研究[J]. 航空学报, 2006, 27(3):395-398.
Yang Yongnian, Yang Qing, Xiao Chunsheng, et al. Investigation of flow and twin-vertiacl tail buffet characteristica of leading-edge extension configuration[J]. Acta Aeronautica et Astronautica Sinica, 2006, 27(3):395-398.
[11] 陈忠实. 2.4m风洞飞行器抖振边界试验技术研究[C]. 低跨超声速空气动力学交流会论文集, 2004.
Chen Zhongshi. Study on the buffeting boundary test technology of 2.4 meters wind tunnel aircraft[C]. Article Collections of Low Transonic and Supersonic Aerodynamics Exchange Conference, 2004.
[12] 钟德均. 歼击机抖振边界试飞技术研究[J]. 飞行试验, 1995,11(2): 14-19.
Zhong Dejun. Research on flight test technique of fighter buffet boundary[J]. Flight Test, 1995,11(2): 14-19.
[13] 孙勇军, 卢晓东, 刘娟. JL-6飞机抖振边界试飞技术及相关性分析[J]. 飞行力学, 2010, 28(2): 85-88.
Sun Yongjun, lu Xiaodong, Liu Juan. Flight buffet boundary test technique and correlation analysis for JL-6 aircraft[J]. Flight Dynamics, 2010, 28(2): 85-88.
[14] 李劲杰, 杨青, 杨永年, 等. 边条翼布局双垂尾抖振表面脉动压力风洞实验研究[J]. 实验流体力学, 2006, 20(3): 29-32.
Li Jinjie, Yang Qing, Yang Yongnian, et al. The wind-tunnel unsteady pressure measurements of twin-vertical tail during buffet of strake-wing configuration[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(3): 29-32.
[15] 吕志咏, 张明禄, 高杰. 双立尾/三角翼布局的立尾抖振研究[J]. 实验流体力学, 2006, 20(1): 13-16.
Lü Zhiyong, Zhang Minglu, Gao Jie. Study on vertical tail buffeting of configuration with twin vertical tails/delta wing[J]. Journal of Experiments in Fluid Mechanics, 2006, 20(1): 13-16.
[16] 李矩. 确定运输类飞机抖振边界的试飞方法[J]. 飞行力学, 1991, 9(3): 84-91.
Li Ju. Flight test technique for determining buffet boundary of transport category airplanes[J]. Flight Dynamics, 1991, 9(3): 84-91.
作者简介:

李小路(1983-),男,湖北荆州人,硕士,工程师。研究方向:飞机振动、抖振飞行试验。通讯地址:西安市阎良区中国飞行试验研究院飞机所(710089)。E-mail: 89233848@qq.com
