超临界压力正十烷对流传热实验及计算研究
2014-03-29张若凌肖世德张香文乐嘉陵
张 磊, 张若凌, 肖世德, 张香文, 乐嘉陵
(1. 西南交通大学 机械工程学院, 成都 610031; 2. 中国空气动力研究与发展中心 高超声速冲压发动机技术重点实验室, 四川 绵阳 621000; 3. 天津大学 化工学院, 天津 300000)
0 引 言
主动冷却是解决超燃冲压发动机热防护问题的重要技术途径,此时碳氢燃料在喷入燃烧室燃烧前,将作为冷却剂吸收发动机壁面热量[1]。
主动冷却通道呈现典型的细长特征[2],而且通道壁面的热流很大,导致燃料在通道内的流动和传热过程十分复杂。冷却通道内燃料的工作压力一般高于其临界压力(~2.2MPa),温度也将超过其临界温度(~620K),在此过程中燃料的物理化学性质变化剧烈。冷却通道入口附近燃料的流动状态一般为层流,燃料在通道内吸热后,其流动状态往往由层流转变为过渡状态,最后发展为湍流。超临界压力下碳氢燃料对流传热关联式对于超燃冲压发动机的冷却结构设计至关重要[3-4]。
Huber[5]等将过渡区单相对流传热的努赛尔数Nu与Petukhov、Gnielinski和Churchill关联式进行了对比,发现Gnielinski和Churchill关联式与实验数据吻合较好。Nathman[6]等根据Dittus-Boelter(以下简称D-B)关联式和实验数据,采用曲线拟合的方法发展了适用于大高宽比冷却通道内湍流区的传热关联式。Ghajar[7-8]等采用人工神经网络的方法研究了3种不同入口构型的过渡区传热关联式。Yang[9]等通过唯象分析和实验数据评估,采用无因次数对传统的D-B传热关联式进行修正。上述文献中,仅单独针对过渡区或湍流区的传热关联式进行研究,对于流动状态发生剧烈变化的对流传热关联式缺乏系统性的研究,也未结合超燃冲压发动机主动冷却通道的实际应用条件。
在发动机冷却结构设计中,需要比较不同的传热关联式,并检验其适用性,尤其是超临界压力下碳氢燃料在层流和过渡区的传热关联式。本文根据超燃冲压发动机主动冷却通道实际工作条件,开展正十烷电加热管实验,系统地研究超临界压力下层流、过渡和湍流区正十烷的传热关联式。本文的研究结果可以为主动冷却超燃冲压发动机的传热设计提供技术基础。
1 实验装置
如图1所示,电加热管实验装置一般由燃料供应系统、加热系统、数据显示与采集系统、燃料冷却与回收系统等组成。实验工作过程如下:燃料供应系统将液体燃料由燃料贮箱输送至电加热管入口;燃料流过管壁通有电流的管道,并与管壁发生强制对流传热而吸热升温;电加热管出口的高温燃料经冷凝器冷却回收并进行采样分析。
电加热管实验在天津大学电加热设备上进行。电加热管垂直安装在一箱体(长宽高为0.6m×0.6m×2.0m)内。电加热管材料为1Cr18Ni9Ti,与实际发动机冷却通道尺寸相似,内径1.5mm(外径3.0mm),长度1300mm。燃料为正十烷(pc=2.1MPa;Tc=617.7K),燃料供应压力约为4.3MPa。
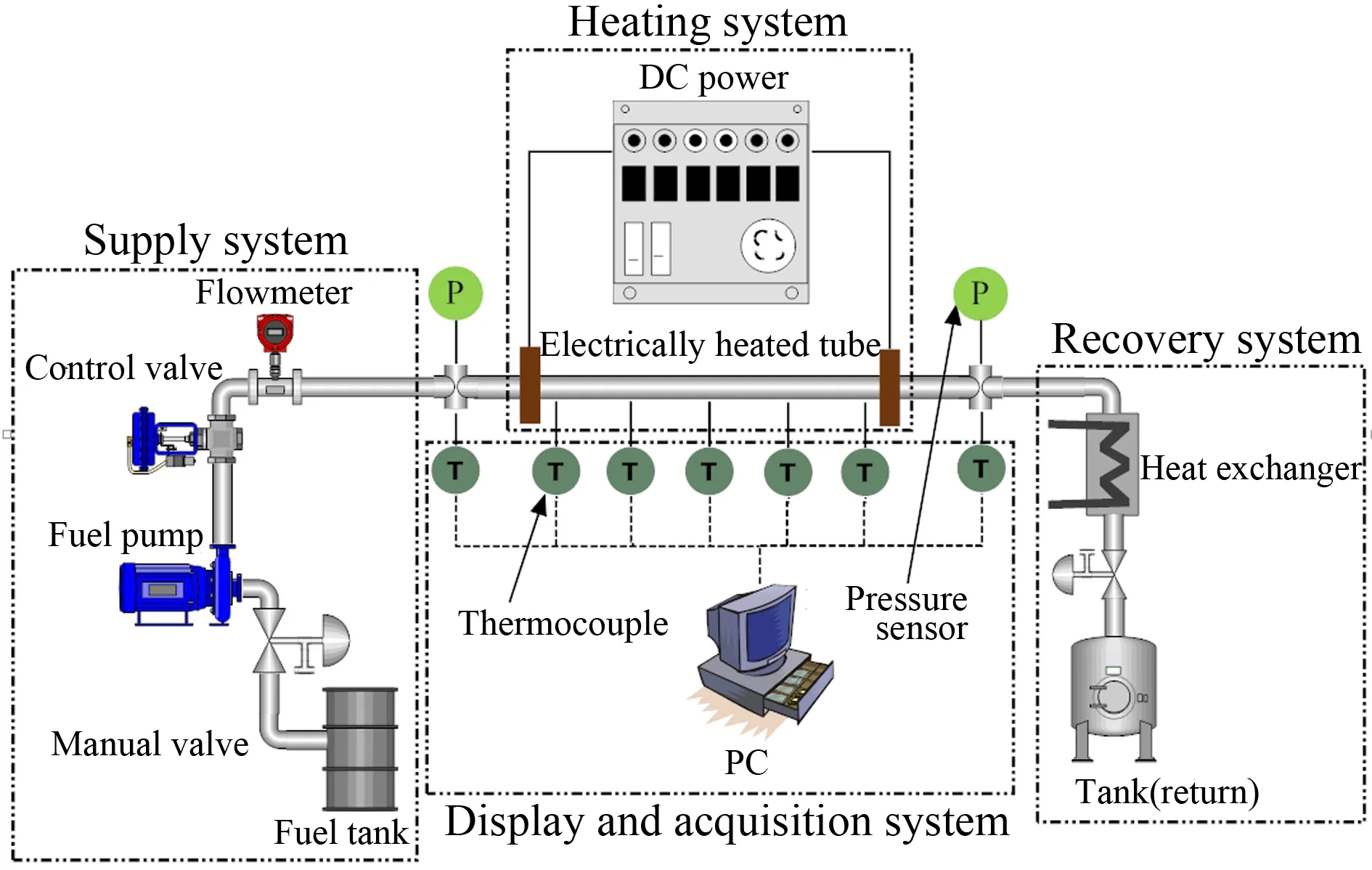
图1 电加热管设备原理图
采用点焊在电加热管外壁上的17个外径0.3mm的K型热电偶测量外壁温度,最大测量误差±3K;采用压阻式压力传感器测量电加热管入口及出口处燃料压力,最大测量误差±0.2%F.S;采用直流电阻电桥测量电加热管的电阻,最大测量误差±0.001Ω;采用铠装热电偶测量电加热管入口及出口处燃料温度,最大测量误差±3K;采用称重法测量燃料的质量流量,最大测量误差±0.01g/s。
一共进行了3次实验,每次实验完成多个稳定工作状态,燃料质量流量分别为0.93、1.24和1.86g/s。实验中通过调节电加热管两端的电压,以控制燃料与管壁之间的热流密度。如图2所示,当管壁的温度达到稳定状态时,对流传热的热流密度也恒定。
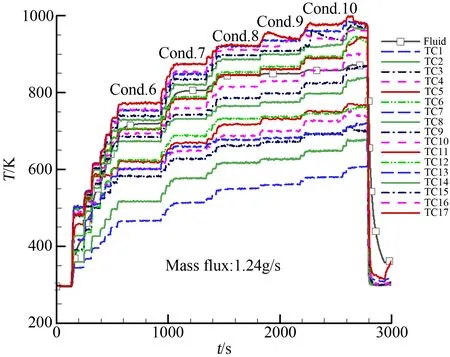
图2 外壁温随时间变化
采用空管校正的方法对电加热管热损失进行标定。由于电加热管内无流体流动,其热损失包括外壁与箱体内空气自然对流传热和管壁的热辐射两部分。假设箱体及其内部的环境温度相同且保持不变,则热损失qloss是外壁温Two和箱体内环境温度Tair的函数:
(1)
当电加热管达到稳定工作状态时,管壁的发热量等于其热损失,不同位置的热损失有所不同。根据实验数据,采用曲线拟合的方法获得外壁温测点处的热损失函数,测点之间管壁的热损失采用线性插值法计算得到。第10个热电偶处(x=0.9m)的管壁热损失曲线如图3所示(Tair=298K)。
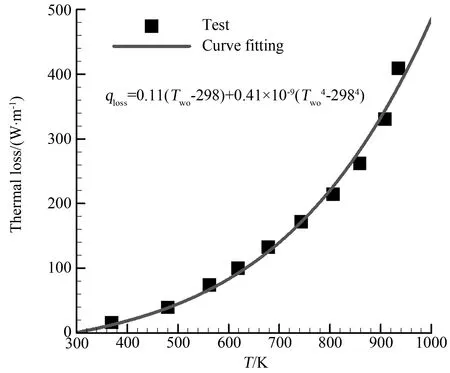
图3 热损失曲线
2 传热关联式计算方法
2.1不同流态的传热关联式
燃料在管内的流动状态取决于当地雷诺数Re,一般准则是:Re<2300时为层流;2300≤Re≤104时为过渡状态;Re>104时为完全湍流[10]。
根据文献[10-11],对于具有常物性,均匀表面热流密度的圆管中充分发展的层流,Nu是个常数,与Re、普朗特数Pr以及轴向位置无关:
Nul0=4.36
(2a)
当燃料主流区温度与表面温度的不同引起燃料物性差别较大时,由上式计算的Nu将会产生影响。对于液体,粘性系数的变化十分重要,特别是对于油类。文献[10-11]建议,对于液体,层流区的传热关联式修正如下:
Nul=Nul0(μ/μw)n
(2b)
式中:μ、μw为燃料平均温度下和表面温度下的动力粘度。上式中的修正系数,可以应用于圆管内充分发展或入口区的层流流动。
过渡区广泛采用的是Gnielinski整理的两种关联式[10,12]。Gnielinski关联式1的形式如下:
f=(1.82lgRe-1.64)-2
上式的适用范围为:0.5≤Pr≤2000,2300≤Re≤5×106。
Gnielinski关联式2的形式为:
Nutr2=0.012(Re0.87-280)Pr0.4
(3b)
上式的适用范围为:1.5≤Pr≤500,3000≤Re≤106。
过渡区采用的另一种形式是Petukhov关联式[5,12],
C=1.07+900/Re-[0.63/(1+10Pr)]
上式的适用范围为:1.5 计算光滑圆管内充分发展的湍流,采用的是D-B关联式[10-11,13] Nut1=0.023Re0.8Prn (4a) 其中,加热时n=0.4。实验证实上式的适用范围为:0.7 D-B关联式可用于小到中等的温差,对于物性变化较大的流动,广泛采用的是Sieder-Tate(以下简称S-T)关联式[10,11,13] Nut2=0.027Re0.8Pr1/3(μ/μw)0.14 (4b) 上式的适用范围为:0.7 以上各式中,如果已知Nu、Re和Pr,以及燃料的动力粘度,则可以采用最小二乘法拟合传热关联式中的各系数或者给出新形式的传热关联式。Nu、Re和Pr的计算方法参见下节。 2.2努赛尔数的确定方法 电加热管传热示意如图4所示。电流流经管壁时会产生热量使管壁升温,管壁与管道内的燃料发生对流传热,燃料温度在流动方向上逐渐升高。这一过程相当于有内热源的圆管内部强制对流传热。 图4 电加热管传热示意 由于沿轴向传热的热流密度和热流量相比于径向很小,故可忽略。采用一维对流传热来处理电加热管内燃料的流动。 实验努赛尔数Nue按下式进行计算[10-11] Nue=hdi/λ (5) 式中:h是燃料与内壁面的对流传热系数,di是管子的内径,λ是燃料的热导率。h的计算式为[10-11] h=q/(Twi-Tl) (6) 式中:q是内壁处的热流密度,Twi是内壁温,Tl是燃料在截面上的平均温度。热流q与电流I、单位管长电阻R以及热损失qloss相关,按下式计算: q=(I2R-qloss)/πdi (7) 对于管壁内有热源的圆管,内外壁温的关系为 (8) 式中:do是管子外径,λw是管壁的热导率。 燃料的雷诺数Re和Pr计算公式如下 Re=ρudi/μ (9) Pr=cpμ/λ (10) 式中:cp是定压比热,u和ρ为燃料流速和密度。燃料流速u可以根据质量守恒关系得到 (11) 以上公式中燃料的密度、定压比热、粘性系数以及热导率是根据微元段入口燃料的温度和压力,利用碳氢混合物物性程序计算得到。从电加热管入口沿流向进行推进计算中,需要确定微元段燃料的温升和压力损失。 对于微元段Δl,根据能量守恒计算燃料的温升 (12) 式中:ΔhT是显焓增加量。假定燃料不发生裂解反应,则燃料所吸收的热量均转化为显焓。 燃料的压力损失按下式进行计算 Δp=0.5fρu2Δl/di (13) 其中,摩擦系数f简单定义为[10-11] (14) 3.1管壁热流密度 一个实验状态中,内壁热流密度沿管长分布如图5所示。在管长0~0.2m及1.2~1.3m之间,由于电加热管向两端连接物体传热的影响,使得热流密度下降比较严重,这与超燃发动机实际工作条件有所不同。下文中将采用管长0.2~1.2m之间的数据进行研究。 图5 热流沿管长分布 3.2外壁温及燃料温度 4个实验状态中外壁温沿管长分布如图6所示。不同实验状态中,电加热管最高外壁温范围400~996K,电加热管出口正十烷温度范围335~870K。 图6 外壁温沿管长分布 一个实验状态中,根据一维质量和能量守恒关系计算的正十烷温度沿管长方向分布如图7所示。 一个实验状态中,燃料Re由入口处约1100升高至出口处约55000;Pr由入口处约14减小至出口处约1,如图8所示。由此可见,管内正十烷物性变化范围很大,燃料的流动状态经历了层流、过渡和湍流。 图7 正十烷温度沿管长分布 图8 Re和Pr沿管长分布 3.3传热关联式计算 3.3.1层流区 一个实验状态中,Re、Nue分布如图9所示。由Re分布可知,在管长0.2~0.9m之间,正十烷流动状态属于层流(管长0~0.2m之间,Nue有较明显的入口效应[10])。 在本实验条件下得到的实验数据表明,层流区Nu强烈与入口雷诺数Reen相关,假定其形式为 采用最小二乘曲线拟合的方法,对层流区Nue进行分析,得到层流区正十烷传热关联式的结果为 将上式与实验结果进行对比,如图9所示。上式的计算结果比式(2b)大,可能是由壁面粗糙度以及入口效应引起。 图9 层流区Nu沿管长分布 3.3.2过渡区 将Gnielinski关联式1和关联式2、Petukhov关联式应用在一个实验状态中,与Nue进行对比,如图10所示。由图可见,在过渡区Gnielinski关联式1和Gnielinski关联式2比Petukhov关联式具有更好的适用性,但与实验值的误差也较大。 图10 过渡区不同关联式与实验值对比 在图10中作者给出了一个过渡区的传热关联式,其形式为 Nutr=(1-f(θ))Nul+f(θ)Nut (16a) (16c) 式中:Nul是式(15b)表示的层流区努赛尔数,Nut是湍流区努赛尔数(见下节式(17)),采用上式的计算结果如图10所示。可以发现,采用上式的计算结果与实验值吻合得更好。 3.3.3湍流区 将Gnielinski关联式1和关联式2、S-T和D-B关联式应用在一个实验状态中,与Nue进行对比,如图11所示。由图可见,S-T关联式具有较好的适用性。Gnielinski关联式1和关联式2,D-B关联式的计算结果偏低。 图11 湍流区不同关联式与实验值对比 针对S-T关联式的形式,采用最小二乘曲线拟合的方法,对实验中湍流区Nue进行分析,得到湍流区正十烷的传热关联式如下: Nut=0.020Re0.82Pr0.40(μ/μw)0.16 (17) 将上式的计算结果与S-T关联式进行对比,如图11所示。由图可知,式(17)和S-T关联式的结果数值很接近,与实验结果吻合得较好。 研究中发现湍流区Nu对外壁温十分敏感,需要提高外壁温测量的精度以获得更加准确的Nu。 3.4外壁温对比 检验传热关联式的适用性对超燃冲压发动机冷却结构设计至关重要。根据传热关联式和壁面热流密度,可以计算外壁温,并与实验结果进行对比。这与超燃冲压发动机主动冷却传热计算中获得外壁温的过程类似,但是与获得传热关联式的步骤相反。因此,需要选择与计算传热关联式不同的实验状态进行计算。 根据本实验得到的传热关联式(式(15)~(17)),以及其余实验状态中的质量和能量守恒关系,可以计算电加热管的外壁温,并与外壁温的测量值进行对比。根据式(5)、(12)计算燃料温度,由式(6)、(7)计算内壁温,然后根据式(8)计算外壁温。 3个实验状态中,将外壁温的计算值与实验值进行对比,如图12(a)、(b)和(c)所示。 图12表明,对于3种流态下外壁温的计算值与实验值吻合得均较好。 (a) Laminar flow region (b) Transition flow region (c) Turbulent flow region 利用电加热管设备,开展了超临界压力正十烷对流传热实验及计算研究,得出以下结论: (1) 正十烷在电加热管物性变化范围大,流动经历了层流、过渡和湍流3种流动状态; (2) 利用燃料管道传热关联式计算方法,利用实验数据,得到了超临界压力正十烷的层流、过渡和湍流区对流传热关联式; (3) 根据给出的传热关联式,进行了电加热管外壁温计算值与实验值的对比研究。结果表明,本实验得出的正十烷传热关联式具有较好的适用性。 参考文献: [1]江晨曦, 仲峰泉, 范学军, 等. 超临界压力下航空煤油流动与传热特性实验[J]. 推进技术, 2010, 31(2): 230-234. Jiang C X, Zhong F Q, Fan X J, et al. Experiment on convective heat transfer of aviation kerosene under supercritical pressures[J]. Journal of Propulsion Technology, 2010, 31(2): 230-234. [2]Kandlikar S G, Grande W J. Evolution of microchannel flow passages-Thermo-hydraulic performance and fabrication technology[J]. Heat Transfer Engineering, 2003, 24(1): 3-17. [3]Jackson T A, Eklund D R, Fink A J. High speed propulsion: Performance advantage of advanced materials[J]. Journal of Materials Science, 2004, 39: 5905-5913. [4]Faulkner R F, Weber J W. Hydrocarbon scramjet propulsion system development, demonstration and application[R]. AIAA 1999-4922. [5]Huber D, Walter H. Forced convection heat transfer in the transition region between laminar and turbulent flow for a vertical circular tube[C]. Latest Trends on Theoretical and Applied Mechanics, Fluid Mechanics and Heat & Mass Transfer, Corfu Island, Greece, July 22-24, 2010. [6]Nathman J, Niehaus J, Sturgis J C, et al. Preliminary study of heat transfer correlation development and pressure loss behavior in curved high aspect ratio coolant channels[R]. AIAA 2008-5237. [7]Ghajar A J, Tam L M, Tam S C. Improved heat transfer correlation in the transition region for a circular tube with three inlet configurations using artificial neural networks[J]. Heat Transfer Engineering, 2004, 25(2): 30-40. [8]Ghajar A J, Tam L M. Heat transfer measurements and correlations in the transition region for a circular tube with three different inlet configurations[J]. Experimental Thermal and Fluid Science, 1994, 8: 79-90. [9]Yang Y H, Xu C, Huang S F. A new heat transfer correlation for supercritical fluids[J]. Front Energy Power Eng, 2009, 3(2): 226-232. [10] Bergman T L, Lavine A S, Incropera F P, et al. Fundamentals of heat and mass transfer[M]. 7th edition. New York: John Wiley & Sons, Inc., 2011. [11] Kays W, Crawford M, Weigand B. Convective heat and mass transfer[M]. 4th edition. New York: McGraw-Hill Book Company, Inc., 2005. [12] Rohsenow W M, Hartnett J P, Cho Y I. Handbook of heat transfer[M]. 3rd edition. New York: McGraw-Hill Book Company, Inc., 1998. [13] Linne D L, Meyer M L, Edwards T, et al. Evaluation of heat transfer and thermal stability of supercritical JP-7 Fuel[R]. AIAA 97-3041. [14] 王英杰, 徐国强, 邓宏武, 等. 超临界RP-3管内换热特性实验[J]. 推进技术, 2009, 30(6): 656-660. Wang Y J, Xu G Q, Deng H W, et al. Experimental investigation on heat transfer of supercritical RP-3[J]. Journal of Propulsion Technology, 2009, 30(6): 656-660. 作者简介: 张磊(1985-),男,湖北襄阳人,博士生。研究方向:碳氢燃料冷却超燃冲压发动机。通讯地址:四川省绵阳市211信箱高超中心二室(621000)。E-mail: zl20051038@163.com
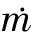
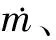
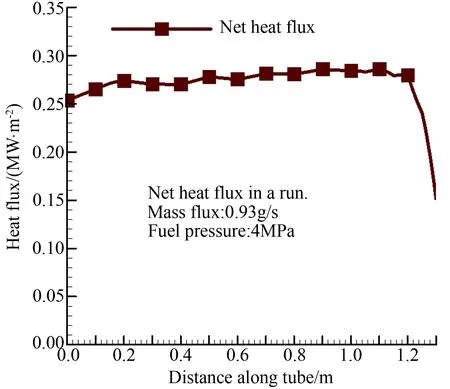
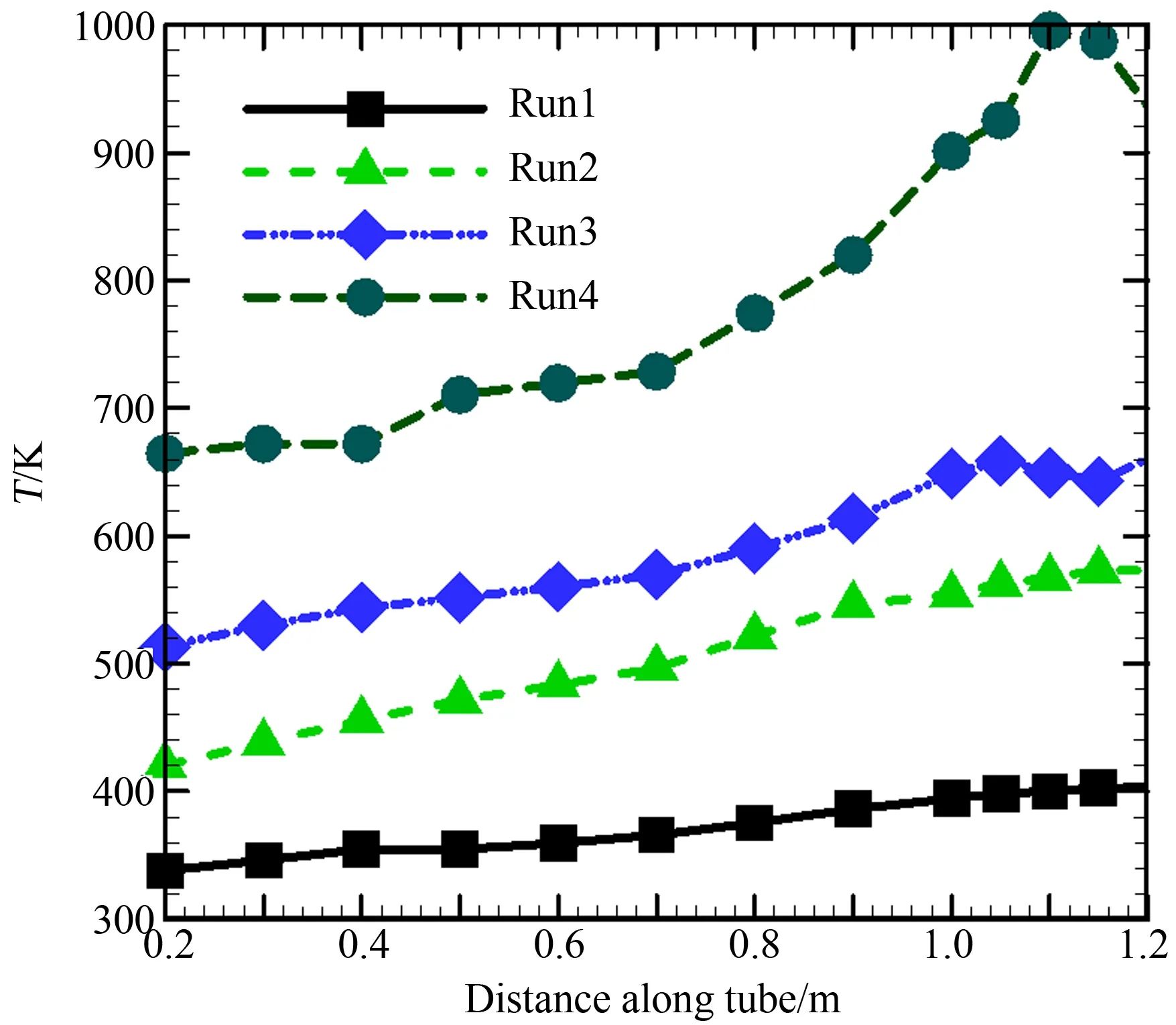
3 实验结果及计算分析


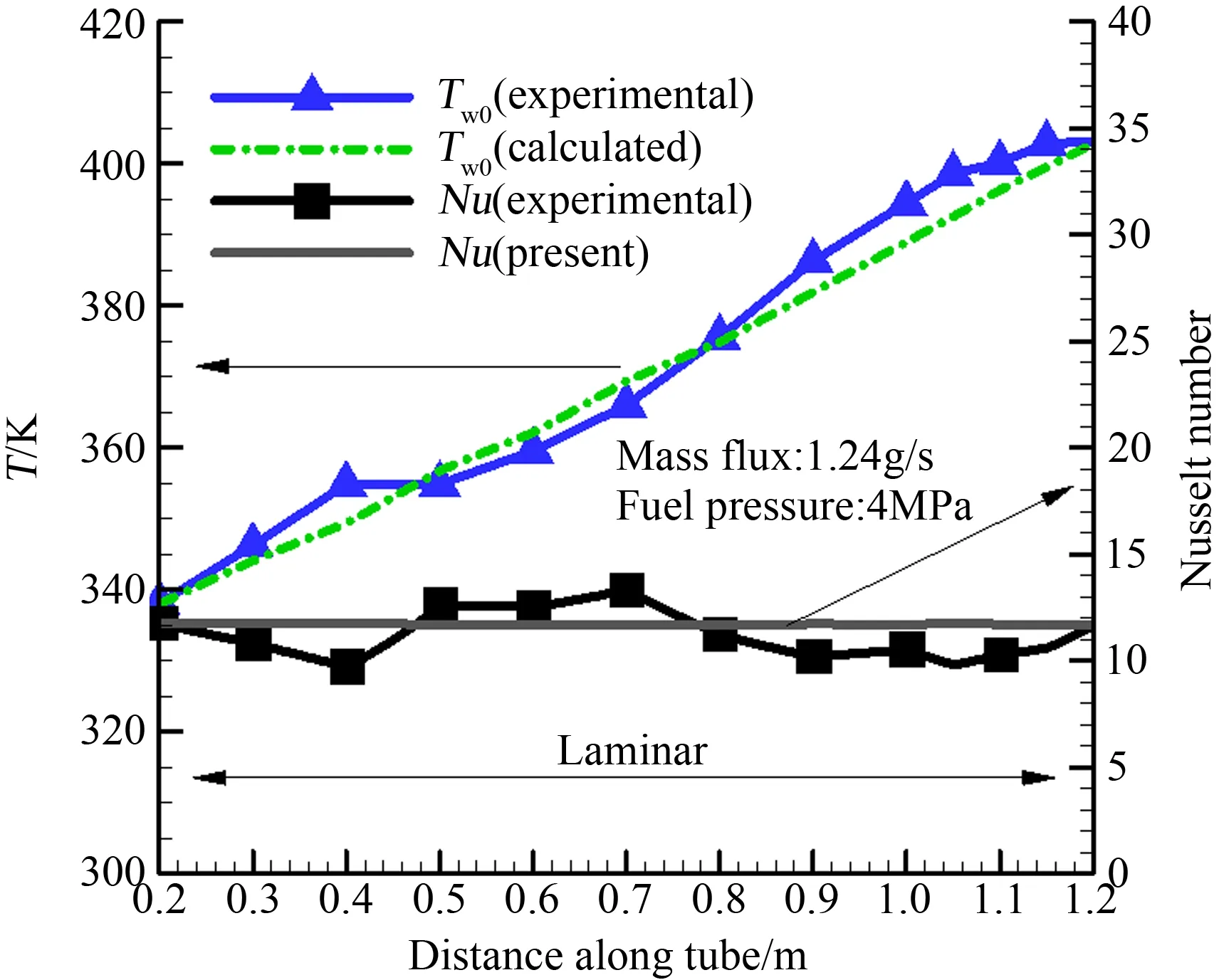
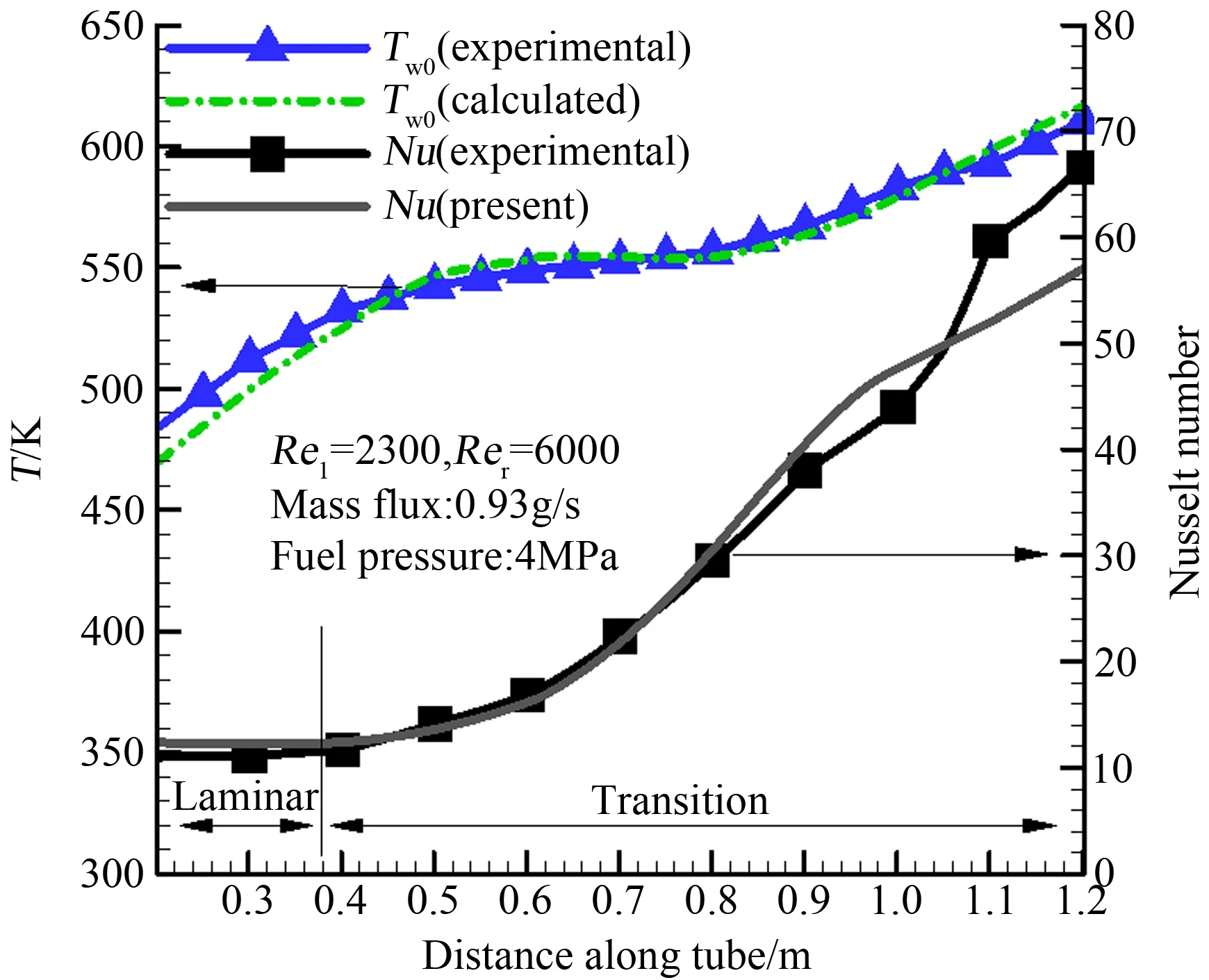
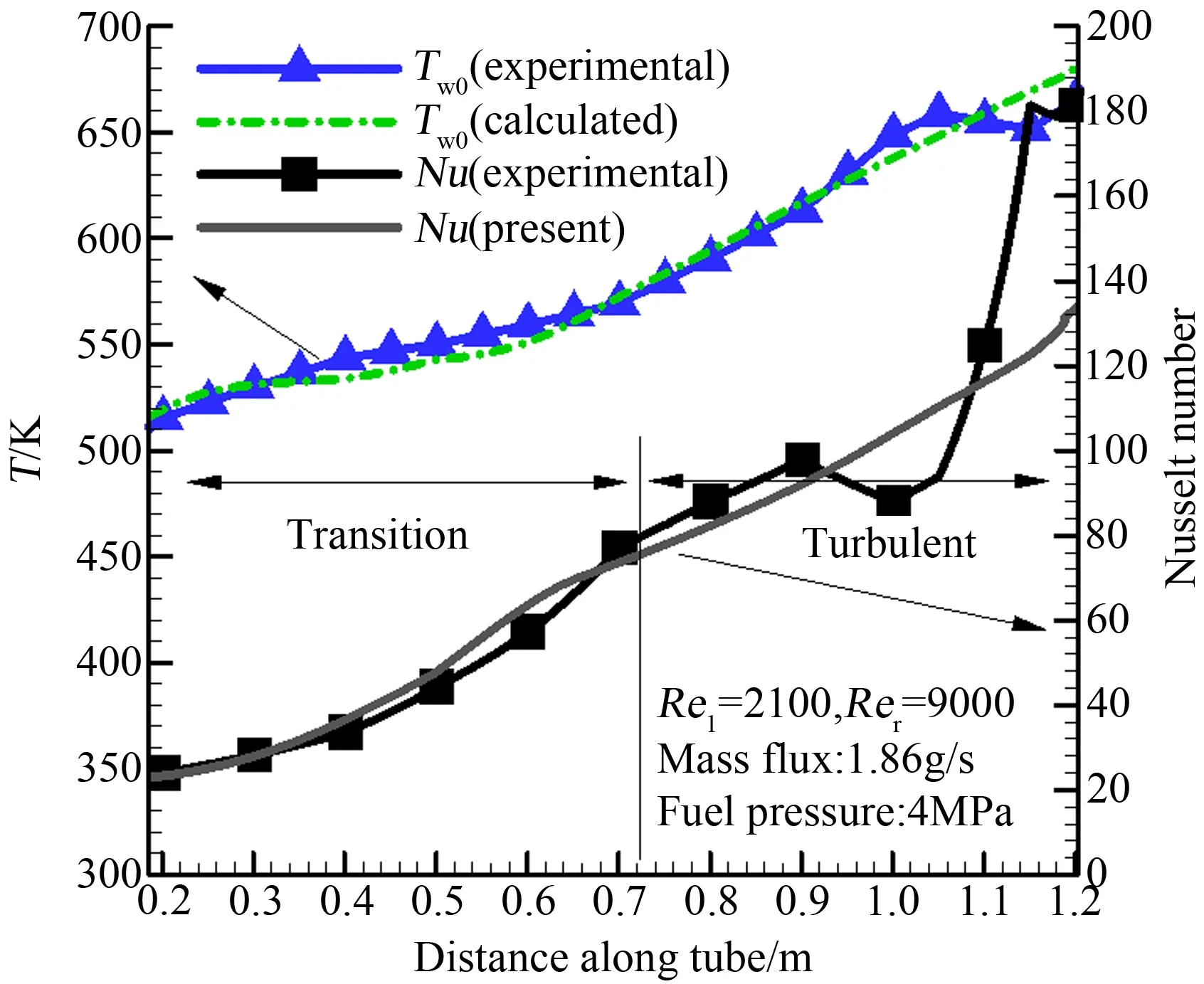
4 结 论

