基于上升管压力脉动标准差快速预报喷动床颗粒聚团现象
2014-03-28周云龙李洪伟
周云龙,杨 宁,李洪伟
(东北电力大学能源与动力工程学院,吉林 吉林 132012)
喷动床具有良好的传热、传质能力,但其气固两相流动复杂多变,因此关于其动力学特性的认识至今仍是许多学者研究的热点[1]。喷动床在较低的喷动气流速度下会出现颗粒的聚团现象,这种现象的发生将会影响喷动床颗粒的流动以及传热过程,严重时还会导致喷动床的反流态化状态。
喷动床压力脉动信号是床内两相动力学众多内在因素的综合反应。为改善喷动床内气固流动特性,近年来国内外学者普遍致力于提取压力脉动信号的相关信息并加以利用,其中常用的方法有傅里叶分析、短时傅里叶分析Wigner-Ville分布、Wavelet分析等时频二维谱分析[2-5],通过这些分析方法在压力脉动信号中获取了大量的线性和非线性的特征信息与参数,但上述方法受Heisenberg不确定原理的制约以及时频分辨率、傅里叶分析的局限,存在截断与泄漏等问题。混沌分析和重复率分析方法[6-10]是研究气固流化床混沌动力学特征的有效手段,然而由于特征参数提取的长时间序列的计算要求和流化状态瞬变之间的矛盾难以解决,使得计算结果随参数设置的变化很大。
虽然国内外学者在喷动床内颗粒流动状态的改进以及预测方面做了大量的工作,但未能研制出一种快速有效的预测喷动床颗粒聚团现象的方法。本工作通过在上升管压力测点的下方布置清洗气流,调节通带滤波的界限频率,在消除清洗气流对压力脉动信号影响的前提下,采用了上升管压力测点脉动标准差的方法进行了喷动床颗粒聚团现象的预报,并与Sasic等[11]采用的平均压力降测量方法在颗粒聚团现象的表观速度识别率以及响应时间方面进行了比较。
1 实验流程
本实验在多路差压喷动床实验装置上进行,实验流程如图1所示。来自罗茨风机的空气经过涡街流量计后进入上升管道,颗粒由给料机送入上升管道与空气混合后,由锥形喷嘴引入床内,最后经过旋风分离器过滤后排空。本实验使用的颗粒是玻璃颗粒,颗粒SMD索特尔平均直径为1 mm,颗粒的尺寸分布见图2所示。

图1 实验流程Fig.1 Spouted bed test system

图2 玻璃颗粒的尺寸分布Fig.2 Glass particle size distribution
喷动床上升管自下而上标高为82,115,145,182,225,264 mm的位置设置压力测点,通过罗斯蒙特压力变送器测量每一个测点处的压力,在每一个压力测点的下面都设有清洗气流,可以及时对进入压力测点的颗粒进行吹扫,避免了固体颗粒对压力测点产生堵塞。清洗气流的存在势必会对压力的测量过程造成影响,采用通带滤波对压力变送器采集的数据进行处理,通过调节通带滤波能够使喷动床上升管流体流动对应的频率分量通过,将清洗气流所带来的附加频率分量衰减到极低水平。
以上升管标高为82 mm的测点在表观气速u0为16 m/s时所测量的压力脉动时序图像为例来研究通带滤波器的滤波频率界限设置。喷动床压力脉动的响应时间过长会导致颗粒聚团现象预报失误,如图3(a)所示,滤波器中使用的下限截断频率为0.15 Hz,在100 s突然关闭气流时,压力并没有直接变化到0,而是先降低然后再逐渐变化到0,说明这种滤波状态下压力脉动的响应时间较长,不能很好地反映床内气固两相流的运动状况。逐渐将下限截断频率增加到0.45 Hz时,虽然压力脉动的响应时间有所减小,但关闭气流的瞬间压力均呈现先降低然后逐渐变化到0的趋势。当下限截断频率提高到0.5 Hz时,从图3(b)可以看到,100 s突然关闭气体后,压力脉动较快地降低到0,响应时间被大大缩短。经对比选用下限截断频率为0.5 Hz的滤波方法可以较快、较准确的反映喷动床气固两相流的流动状态。

图3 压力时间序列Fig.3 Pressure time-series
图4为清洗气流分别为2,3,5 m/s对应的压力脉动功率谱,当频率大于6 Hz时,由于清洗气流流速的变化,导致压力脉动的功率谱密度发生较大的变化,当频率小于6 Hz时,压力脉动的功率谱密度几乎不随清洗气流流速的变化而变化,说明在此频率范围内,清洗气流对喷动床的压力脉动特性影响最小,综上所述,选取通带滤波的的频率为0.5~6 Hz。
尽管清洗气流的流速对压力脉动信号的影响可以通过前述通带滤波方式降低,但是实验研究发现,在清洗气流流速为2 m/s时就可以保证颗粒不会对压力测点造成堵塞,所以本实验使用的清洗气流流速为2 m/s。实验数据采集系统使用的是IDTS-4516U型16通道数据采集器,数据采集器将经过通带滤波处理后上升管不同标高处的压力信号传送给电脑。实验数据采样频率为400 Hz,采样时间为120 s,实验表观气速的变化范围为0~20 m/s,实验测得颗粒的最小喷动速度为1.5 m/s。
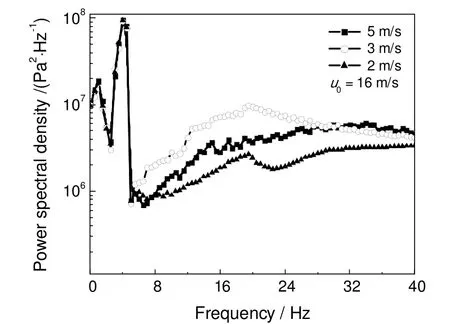
图4 不同清洗气速下功率谱Fig.4 Power spectrum at different purge air velocity
2 实验结果与分析
工业上经常利用床体的平均压力降来检验喷动床内颗粒的流动状态,这是因为喷动床内的压力信号可以体现床内气、固两相流动的许多动态信息,是中心射流、气泡、颗粒特性以及床体几何特性等多种因素的综合反映,对床内流体力学、气固混合、传热传质和化学反应都有较大的影响[11-12]。但是喷动床内的颗粒聚团现象经常发生在表观气速相对较小的工况,为了验证本研究提出的压力脉动标准差方法在表观气速识别能力以及聚团现象预报响应时间方面的优越性,将压力脉动标准差预报方法与Sasic等[11]提出的床层压力降预报方法进行了比较。
2.1 表观气速识别能力
本实验中压力降定义为给定标高处的测点压力与上一测点压力之差。图5不同表观气速下,喷动床上升管不同标高处压力测点平均压力降的变化趋势。从图中可以看出平均压力降随着表观气速的变化不是十分明显,这是因为影响各测点处平均压降变化的主要因素是床层密度,表观气速为1.5~20 m/s时,喷动床内颗粒是稳定喷动状态,床层的密度是恒定的,对应的平均压力降几乎不受表观气速的影响,只有当表观气速从1.5 m/s降低到0 m/s时,喷动床内的颗粒逐渐由稳定喷动状态向固定床状态转变,床层密度发生改变,床层的平均压力降随着表观气速的减小迅速降低到0。表明在使用平均压力降进行颗粒聚团的预报时,仅仅当喷动床转变为固定床状态时,平均压力降才发生较大的变化,此时喷动床内的颗粒早已发生聚团,本方法的速度识别范围较窄,不能够在聚团状态发生之前给予一定的预报。
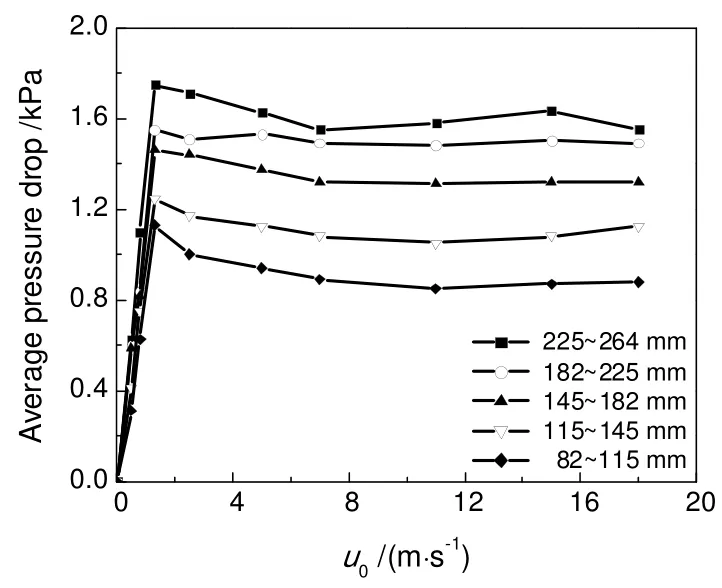
图5 不同表观气速下上升管平均压力降分布Fig.5 Average pressure drop distribution along rising pipe at different superficial gas velocity
相比于平均压力降的预报方法,考察了本研究提出的随着表观气速变化的压力标准差测量法。图6为喷动床在不同表观气速时,上升管不同标高处压力测点压力脉动标准差的变化趋势,从图中可以看到,这种预报方法在相应的表观气速范围内,压力脉动的标准偏差随着表观气速的增加发生了较为剧烈的变化。这就意味着利用压力脉动的标准差预报方法相比于平均压力降预报方法可以更好的识别不同的表观气速。从而实现了在较低的表观气速范围内进行颗粒聚团现象的预报。
2.2 预报响应时间
由于颗粒聚团现象发生在表观气速相对较低的范围,从图6可以看出,在表观速度相对较低的区域,不同标高处压力脉动标准差随着表观气速的变化呈现线性变化规律。压力脉动标准差E(S)与表观气速的关系可以通过式(1)的形式表示

图6 压力脉动标准差随表观气速变化曲线Fig.6 Pressure pulsation standard deviation curve along with the superficial gas velocity

式中,σ为压力脉动标准差;S为压力脉动标准差的期望值;a,b为常数,b大于等于0。压力脉动标准差期望值S服从标准正态分布。
若n个变量S1、S2、……、Sn独立且均为标准正态分布,则这n个服从标准正态分布的随机变量成一个新的随机变量x2,其分布规律称为卡方分布[13]。若服从卡方分布的变量包含有n个独立的随机变量和由它们所构成的k个样本统计量,则卡方分布表达式的自由度为n-k。因此当测量n个压力脉动标准差时,卡方分布具有n-1阶自由度,压力脉动标准差的卡方分布表达式如下

通过(1)(2)两式,可以得到式(3)压力脉动标准差S小于一个给定的颗粒聚团预报压力T的发生率关系式

从式(3)可以看出颗粒聚团预报发生率P与表观流速 、预报压力T有关。其中预报压力T即颗粒发生聚团现象时对应的压力,当上升管压力小于预报压力时颗粒的聚团现象随即发生,通过式(3)可以计算出在不同的表观气速下,压力脉动标准偏差小于给定颗粒聚团预报压力的发生率,以上升管标高为82 mm的测点为例,计算结果如图7所示。
为了验证上述计算所得颗粒聚团发生率模型的正确性,通过调节表观气速,观察喷动床内颗粒的运动情况,当喷动床聚团现象发生时,记录上升管不同标高位置对应的压力值并将其转换为相应的压力脉动标准差。上升管标高为82 mm的测点压力脉动标准差在不同表观气速的测量结果见表1,通过表1可以发现压力脉动标准差的测量值和颗粒聚团发生率模型计算值的误差范围均小于5%,这说明计算所得颗粒聚团发生率模型成立。

图7 颗粒聚团发生率曲线Fig.7 Particle agglomerate incidence curve

表1 不同表观气速下颗粒聚团模型计算压力脉动标准差及实验值Table 1 Model and experiment pressure pulsation standard deviations at different superficial gas velocities
选用喷动床压力测点标高为82 mm,表观气速为3 m/s,颗粒聚团预报压力值50 Pa的实验工况,比对平均压力降预报方法与压力脉动标准差预报方法在检测颗粒聚团现象时的速度,当60 s时刻,完全关闭气流,平均压力降、压力脉动的标准差随着时间的变化曲线如图8所示。

图8 压力脉动标准差、平均压力降随时间变化曲线Fig.8 Pressure pulsation standard deviation and average pressure drop curve along with time
从图8中可以看到,在小于60 s时,压力脉动标准差与平均压力降随着时间的变化相对比较平稳,这是因为此时喷动气流比较平稳,喷动床内的固体颗粒处于完全流化的状态,然而当60 s时,表观流速突然减小至0 m/s时,压力脉动的标准差与平均压力降都呈现不同的下降趋势,上升管压力脉动标准差在时间为89 s时达到了颗粒预报压力50 Pa,而平均压力降在时间为97 s的时刻才达到预报压力。上升管压力脉动的标准差在达到颗粒聚团预报压力时所对应的时间明显低于平均压力降所对应的时间,这说明上升管压力脉动标准差预报方法实现了对颗粒聚团现象的快速预报。
3 结 论
a)为了保证压力测量过程中颗粒对压力测点不产生堵塞,在每一个压力测点的下面都布置有流速为2 m/s的清洗气流。通过将通带滤波的界限频率设置为0.5~6 Hz,可以保证采集压力数据的响应时间较快,并且在数据采集过程中不受清洗气流的影响。
b)颗粒聚团现象发生在较低的表观气速下,上升管平均压力降预报方法随着表观气速的变化不是十分明显,只有当表观气速接近于0 m/s时,平均压力降才会降低到0。上升管压力脉动标准差预报随着表观气速的增加线性增加,上升管压力脉动标准差预报方法对不同的表观气速有较高的识别性。
c)在较低的表观气速下,基于上升管压力脉动标准差服从卡方分布,提出了预报颗粒聚团发生率模型,通过实验测量颗粒聚团时对应的压力脉动标准差与模型计算结果进行对比,验证了模型的正确性。相比于上升管平均压降预报方法,上升管压力脉动标准差预报方法将颗粒聚团现象预报的响应时间缩短到89 s,实现了颗粒聚团现象的快速预报。
[1] 张 勇, 金保升, 钟文琪. 喷动气固流化床颗粒混合规律的实验研究 [J]. 中国电机工程学报, 2008, 28(20):8-14.Zhang Yong, Jin Baosheng, Zhong Wenqi. Experimental investigation on particle mixing in spout-fluid bed [J]. Proceedings of the CSEE,2008, 28(20):8-14.
[2] Sedighikamal H, Zarghami R. Dynamic characteristics of bubbling fluidization through recurrence rate analysis of pressure fluctuations [J]. Particuology, 2013, 11(3):282-287.
[3] 黄 海, 黄轶伦, 张卫东. 气固流化床压力脉动信号的Wigner谱分析 [J]. 化工学报, 1999, 50(4):477-482.Huang Hai, Huang Yilun, Zhang Weidong. Pressure fluctuations analysis of gas-solid fluidized bed using the wigner distribution [J].Journal of Chemical Industry and Engineering, 1999, 50(4):477-482.
[4] 钟文琪, 章名耀. 基于信息熵分析的喷动流化床流动特性 [J]. 化工学报, 2005, 56(12):2303-2308.Zhong Wenqi, Zhang Mingyao. Flow characteristics in spou-t fluid bed by Shannon entropy analysis [J]. Journal of Chemical Industry and Engineering, 2005, 56(12):2303-2308.
[5] Zhen L, Wang X P, Huang H, et al. Wavelet analysis of pressure fluctuation signals in a gas-solid fluidized bed [J].Journal of Zhejinag University (Science), 2002, 3(1):52-56.
[6] Bai D, Bi H T, Grace J R. Chaotic behavior of fluidized beds based on pressure and voidage fluctuations [J]. AIChE Journal, 1997,43(5):1357-1361.
[7] Daw C S, Lawkins W F, Downing D J, et al. Chaotic characteristics of a complex gas-solids flow [J]. Physical Review A, 1990,41(2):1179-1181.
[8] Fan L T, Kang Y, Neogi D, et al. Fractal analysis of fluidized particle behavior in liquid-solid fluidized beds [J]. AIChE Journal, 1993,39(3):513-517.
[9] Hay J M, Nelson B H, Briens C L, et al. The calculation of the characteristics of a chaotic attractor in a gas-solid fluidized bed [J].Chemical Engineering Science, 1995, 50(3):373-379.
[10] 黄 蓓, 陈伯川, 黄轶伦. 算法复杂性在气固流化床动力学中的多尺度分析 [J]. 化工学报, 2002, 53(12):1270-1275.Huang Bei, Chen Bochuan, Huang Yilun. Analysis of pressure fluctuation in fluidized bed through algorithm complexity in various dcales [J]. Journal of Chemical Industry and Engineering, 2002, 53(12):1270-1275.
[11] Sasic S, Leckner B, Johnsson F. Characterization of fluid dynamics of fluidized beds by analysis of pressure fluctuations [J]. Progress in Energy and Combustion Science, 2007, 33(5):453-496.
[12] 罗 娅, 马增益, 严建华, 等. 图像法用于气-固两相流化床中气泡行为的研究 [J]. 热力发电, 2005, 34(1):16-19.Luo Ya, Ma Zeng yi, Yan Jian hua,et al.Study on gas bubbles behavior in gas solid two phase fluidized bed by using image method [J].Thermal Power Generation, 2005, 34(1):16-19.
[13] Christopher S W, Saralees N, et al. Expansions for the distribution of asymptotically chi-square statistics [J]. Statistical Methodology,2013, 12(5):16-30.
