基于小波和奇异值分解的图像边缘检测

朱晓临， 李雪艳， 邢 燕， 陈 嫚， 朱园珠

(合肥工业大学数学学院，安徽 合肥 230009)

对图像信号而言，剧烈变化的部分如边缘和轮廓携带了重要的特征信息，边缘检测可以找出物体的边界轮廓达到目标识别的目的，因此它在图像处理、计算机视觉、故障诊断、流体力学、地震信号分析、数据压缩等诸多领域具有广泛的应用。基于梯度的边缘检测算子实际上是一个用来增强图像中边缘点的高通滤波器，比如Roberts, Sobel和Prewitt算子[1-3]。经典的边缘检测算子对于高信噪比的图像处理效果很好，但是，因为它们使用一个小模板与图像进行卷积，所以对含有噪声图像处理的效果不佳。为了克服这些问题，Canny[4]提出了一种基于梯度边缘检测的方法，它的滤波器非常近似于高斯函数的一阶导数，但Canny算法在实际应用中存在抗噪能力和边缘定位能力相矛盾的问题。Mallat和Zhong[5]所研究的标准小波变换(WT)也是具有代表性的梯度方法，并且证明Canny边缘检测等同于找出小波变换模的局部极大值。

因为小波变换具有时频局部化的特点和多分辨分析的性质，所以小波分析很适合处理非平稳的信号[6-7]。标准的二维(2-dimensional, 2D)小波变换作为有效的图像处理工具有一段较长且成功的历史。在实际应用中，常常用可分离小波来处理问题；换言之，图像中的行和列被分开处理。这样降低了滤波器设计的复杂性同时使得计算较为简便[8]，所以小波变换常用来作为边缘检测的工具。但是，当检测的图像中含有噪声时，小波边缘检测算子的检测效果要大打折扣[9-10]。

边缘检测在实际生活中的重要应用要求它在处理图像时具有精准的定位。因为图像往往会受到噪声的干扰，影响边缘检测的准确性，而且没有统一的检测方法适用于所有的图像，所以边缘检测仍是图像处理研究的热点。为了充分利用小波变换准确检测突变信号的优良特性，近年来，很多学者对小波边缘检测提出了各种改进的方法。有的方法是将新型小波应用于传统的小波边缘检测[8,11]；有的是将小波和其他方法相结合[9,12]，扬长避短，取其优点；有的是针对小波边缘检测中的阈值选取进行改进[13]。但是上述大部分方法都是针对不含噪的图像进行边缘检测，能取得良好的检测效果，但是对于含噪图像的效果却未必理想；文献[9]中的方法虽然能抑制椒盐噪声，但是得到不是单边缘像素，也就是说，边缘没有被准确定位。

本文首先对图像进行小波变换求取梯度。这样做能够利用小波变换时频分析特点和多分辨分析的性质，尽可能多地找出边缘特征同时抑制噪声。此外，奇异值具有很多良好的性质，而且在图像去噪[14-15]，人脸识别，数字水印[16]等图像处理中有广泛的应用。因为奇异值具有鲁棒性，能够减少噪声的影响。本文将奇异值分解引入边缘检测，在梯度场内应用局部梯度奇异值分解，改良了梯度模值和梯度方向的计算方法，而且用奇异值定义的梯度模值既能增强图像的边缘特征又能抑制噪声。本文方法在无噪声影响的图像中能提取出弱边缘，检测出清晰完整的单边缘，而在有噪声干扰的情况下仍能提取出理想的边缘。

1 二维小波变换

小波变换(wavelet transform, WT)是具有时频分析能力的有力数学工具，在图像消噪和特征提取方面都有很多应用[7]。图像经过小波变换后，对应于突变点处(边缘点)的小波系数绝对值往往都是比较大的，所以信号的局部奇异性与小波变换的模极大值具有十分密切的联系。若取光滑函数的一阶导数作为小波母函数将信号作小波变换，则小波变换的模极大值点对应于信号突变点的位置。通过计算图像信号f的梯度矢量的模极大值来寻找图像边缘的位置，梯度矢量的方向指出了图像灰度值变化最快的方向[6]。为了计算图像信号的两个偏导数，需要具有方向性的可分离二维小波对图像的行和列分别处理。因此，本文对输入的二维图像信号f进行小波变换时，选取光滑函数：

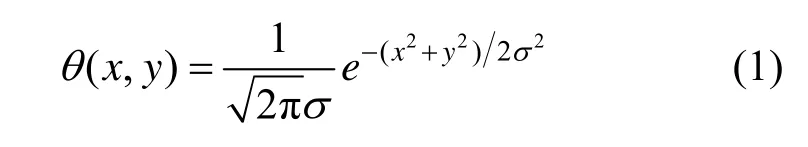
的一阶导数作为母小波：

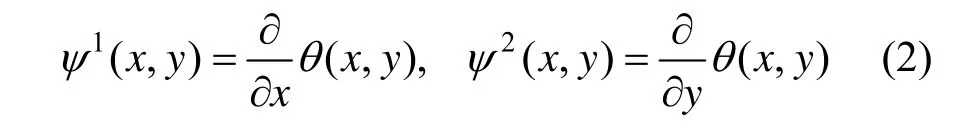
其中*表示定义在L2(ℝ2)上的二维卷积。

用向量的形式表示，f的小波变换可以记为：

其模值和相分别由下式给出：

可以计算在尺度s上的图像边缘：

其中，T是阈值。∠Wsf(x,y)确定图像灰度变化的方向，与边缘方向垂直。

2 图像处理中的奇异值分解

奇异值分解(singular value decomposition, SVD)是数值分析最基本和最重要的工具之一，已经成功应用于去噪、水印、人脸识别等许多图像处理问题。下面简单介绍图像处理中SVD的过程[17-19]。

设一幅图像可表示成m×n矩阵A，A的秩为r,r≤min(m,n)。对A进行奇异值分解：

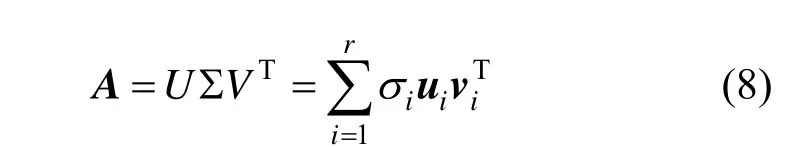
对任意p=1,2,…,m，q=1,2,…,n，up和vq分别称为A的左奇异向量和右奇异向量。

3 基于小波和奇异值分解的边缘检测

图像信号一般都是非平稳信号，而且实际生活中的图像往往还含有噪声。经典边缘检测算子的尺度是不能调整的，但是小波可以随意调整尺度。因为小波的尺度因子和平移因子构成了一个滑动的时频窗，所以，用小波变换对图像进行多分辨分析，就相当于用一个形状、大小和放大倍数可以变换的自适应“放大镜”，可以在时域频域内移动。小尺度下的变换系数对应图像的高频分量，大尺度下的变换系数对应信号的低频分量。于是图像被分解成各个频率下的分量，这样就可以检测对应不同频率的信号。

小波变换还是一种很好的去噪工具。边缘与噪声的区别在于，随着尺度的增加，噪声对应的小波模极大值迅速减小，而边缘的小波模极大值不随尺度的变化而变化，故小波可以在低信噪比的信号中检测出噪声和边缘[7]。本文首先对m×n大小图像进行二维二进小波变换，得到二维二进小波变换的两个分量等价于二维图像f被平滑后图像的梯度矢量的两个分量，则在点(xi,yi)的梯度为：

为了计算局部主方向[20-21]，本文用b×b(模板的大小可以是3×3，5×5，7×7等)大小的模板在m×n的梯度场内移动，然后在b×b的模板内作局部梯度场内的奇异值分解，具体过程如下：首先将模板内梯度排列成如下N×2(N为局部区域内像素的个数)的矩阵G：

然后对矩阵G作如下奇异值分解：

其中，U是一个N×N的正交矩阵，V是一个2×2的正交矩阵，Σ是N×2大小的矩阵：

若将b×b小模板内的梯度场看成一幅图像W，图像W的SVD表明图像W可以用r个基图像的加权表示，其中r是W的秩。奇异值iσ表示第i个基图像Bi对原图W重构的“贡献”大小。Bi对W起作用的图像是

其中，upi和vqi分别是ui和中的元素。若从能量角度看，则图Ci的能量可由下式算出：

因为ui和vi是正交向量，所以

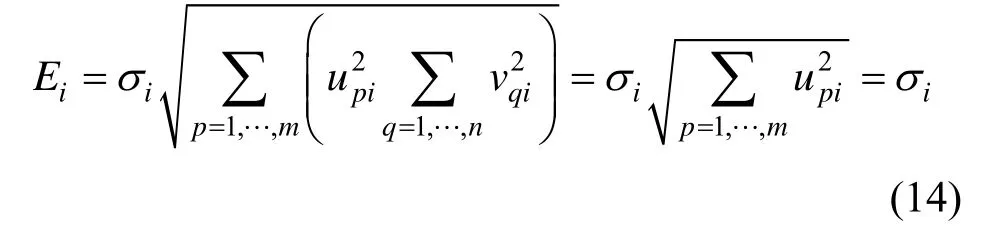
σi表示图像Ci的能量，即σi表示主方向能量[19-20]。

基图像可以和原图很好的匹配，如果增强某些基图像可以突出图像中的细节。现用非线性权和

处理图像，上式可以看作“低通-高通”非线性滤波器。当α＞1时，可以增强较大的奇异值对应的基图像特征；当α＜1时，可以增强较小的奇异值对应的基图像的特征；当α=0时所有的基图像的特征没有改动[22]。

综上所述，奇异值既可以代表图像的能量信息，又能增强图像。本文将局部区域b×b内中心元素(xi,yi)的梯度模值定义如下：

采用Mod(i)作为梯度模值，既可以寻找图像的边缘位置，又对图像中的边缘信息进行了非线性增强，抑制了噪声，这样使得图像中原有内蕴边缘表现得更加突出明显，有利于后续的边缘检测工作。如果Mod值较大，那么这块区域包含丰富的细节信息通过Mod得到强化；如果Mod较小，那么当前区域灰度值变化不明显，几乎没有边缘信息存在。

矩阵V的第2列向量表示局部区域主方向，相应的方向角为：

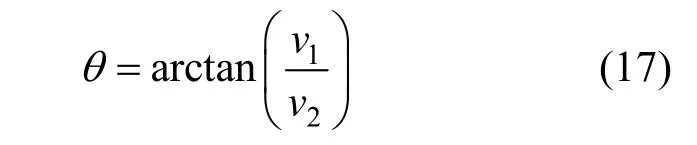
基于SVD具有良好的鲁棒性，以及采用Mod(i)对边缘特征进行了强化，增强了图像的对比度，本文方法能够检测出弱边缘，如图3中第(E0, F1)个图像。当图像受到噪声干扰时，通过上述方法求出的梯度大小和方向不会受到太多影响，使得本文提出的方法对于受到噪声污染较为严重的图像仍能检测出良好的边缘。

本文算法的步骤：

步骤1.对图像进行小波变换。这里选取高斯函数θ(x,y)在x和y方向的一阶方向导数作为母小波，分别沿着水平和垂直方向与图像f进行卷积。若图像中不含有噪声，则小波变换使用小尺度来定位准确的边缘位置；若图像中含有噪声，则小波变换使用大尺度来消除噪声的影响。

步骤2.对于小波求取的梯度矩阵，选取一个b×b大小的模板在梯度场内移动。对于模板内的梯度，作局部梯度奇异值分解。首先是要将模板内的梯度重新排列为N×2的矩阵，然后进行奇异值分解。用得到的奇异值σ1、σ2计算梯度模模值Mod(i)，用矩阵V=[v1v2]的第二列向量计算方向角θ：

这样求取的梯度模值具有增强边缘特征的作用，可以提取出弱边缘。且由于奇异值的稳定性，由上述求取的Mod(i)和θ受噪声影响小，具有良好的抗噪性能。

步骤3.非极大值抑制。对每个像素，沿着梯度方向检测它是否是极大值，若是就保留；若不是这个像素值设为0。

步骤4.用双阈值检测和连接边缘。选择一个高阈值τ1，作用于非极大值抑制后的图像，使得所有梯度模值大于τ1的像素归为边缘。选择一个低阈值τ2＜τ1使得所有梯度模值小于τ2的像素灰度值设为0。若梯度模值大于τ2小于τ1，则该像素归为候选边缘。如果候选边缘点的相邻像素中存在大于τ1的边缘像素，则候选边缘重新列为边缘，否则不是。

4 实验结果

4.1 边缘检测评价标准

边缘检测的质量通常需要考虑主、客观两个方面。图像边缘检测的主观评价标准通常是从人的视觉感受考虑。图像边缘的连续性和光滑程度对于边缘检测算子来说非常重要。在客观评价方面，文中用Pratt品质因数[13]定量评价图像边缘检测算子的性能。

其中，NI和NA分别是理想边缘点的个数和实际检测到的边缘点的个数。α是用于惩罚错位边缘而设定的常数，d是实际检测到的边缘点与理想边缘点的距离，PFOM值越接近1，说明边缘检测效果越好。Pratt品质因数需要给出所测图像的理想边缘，这在实际应用中很难做到。本文将主观判断与Pratt品质因数相结合来评判边缘检测结果的好坏。设在不含噪声情况下用Canny算法检测到的边缘为理想边缘。

4.2 实验结果

为了验证本文所提方法在边缘检测中的有效性，尤其是对于受到噪声污染图像进行边缘检测时的优越性，实验中会对图像分别添加高斯噪声和椒盐噪声进行实验。实验采用大小为256×256的Lena、House图像和大小为232×205的Tire图像，分别采用MATLAB2010a中Canny算法检测边缘，先用非局部均值滤波(non-local means filtering, NLC)去噪后用MATLAB2010a中Canny算法(下面简称为NLMF-C方法)检测边缘，标准2D WT检测边缘，以及本文提出的方法(下面称为Proposed)检测边缘的结果进行比较。由图可以看出：

(1) 在图像未受到噪声干扰的情况下，分别比较图1～3中的A0，C0，E0，G0列可以看出用本文方法检测出来的边缘细节丰富，明显优于小波边缘检测算法，这可由表2中Proposed得到的Pratt品质因数明显高于WT的品质因数看出。有些检测结果比Canny算子的边缘检测效果好。如图2对Tire图像的检测可以看出Proposed方法检测出Tire图像较为完整、连续的轮胎轮廓，而Canny算子检测出的轮胎轮廓是不完整、不连续的。

(2) 在图像受到噪声污染的情况下，本文方法具有良好的抗噪能力，明显优于其他3种方法，下面会给出Pratt品质因数定量评价图像边缘检测算子的性能。

图2中，比较D1行和D4行中的图像，当没有受到噪声污染时，本文方法优于NLMF-C；当受到噪声污染时，两行图像效果相当，但是，本文方法的计算时间远小于NLMF-C方法。两种方法对于处理噪声图像所需时间见表1。

图1 Lena图像(A0，A1，A2，A3列图像是分别对Lena图像添加方差σ=0，10,20,30的高斯噪声进行边缘检测的结果；B0行是Lena图像，B1，B2，B3，B4行是分别采用本文方法(Proposed)，小波方法(WT)，Canny，NLMF-C方法进行边缘检测的结果)

图2 Tire图像(C0，C1，C2，C3列图像是分别对Tire图像添加方差σ=0，10,20,30的高斯噪声进行边缘检测的结果；D0行是Tire图像，D1，D2，D3，D4行是分别采用本文方法(Proposed)，小波方法(WT)，Canny，NLMF-C方法进行边缘检测的结果)

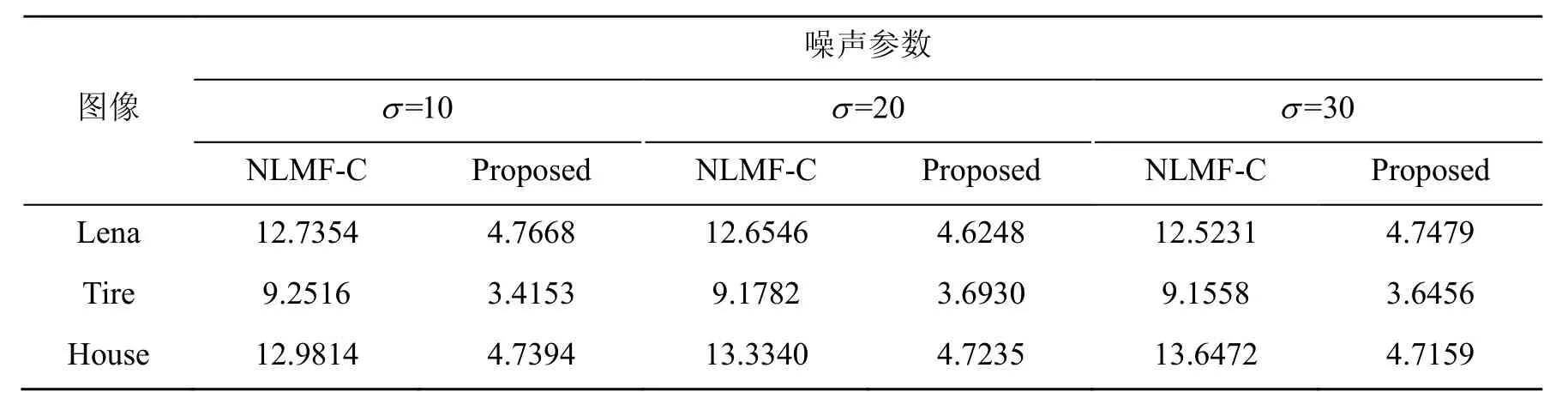
表1 用NLMF-C和本文提出方法(WT-SVD)分别对不同方差(σ=10,20,30)的高斯噪声图像进行边缘检测所需时间对比表

图3 House图像 (E0，E1，E2，E3列图像是分别对House图像添加方差σ=0,0.01,0.02,0.03的椒盐噪声进行边缘检测的结果；F0行是House图像，F1，F2，F3，F4行是分别采用本文方法(Proposed)，小波方法(WT)，Canny，NLMF-C方法进行边缘检测的结果)

表2 不同边缘检测算子分别对不同方差(σ=10,20,30)的高斯噪声Lena图进行边缘检测的Pratt品质因数

5 结 论

小波变换具有“变焦”特性，当尺度较大时，视野宽，主要对低频成分进行分析，可以观察信号的概貌；反之，当尺度较小时，视野窄，主要对高频成分进行分析，可以观察信号的细节。本文方法对图像进行小波变换求取梯度矩阵，旨在利用小波的这一特性提取更多的图像边缘特征。然后在用小波求取的梯度场内进行局部梯度奇异值分解。因为图像的奇异值代表图像的能量信息，表现的是图像的本质特征，具有良好的鲁棒性，利用奇异值定义的经过非线性增强的梯度模值得到的边缘方向信息稳定且准确。因此，本文方法能检测出弱边缘同时抑制噪声。对于不含噪的图像，本文检测出的边缘清晰完整，细节丰富，明显优于小波边缘检测方法。尤其是对于含噪的图像，本文方法对于噪声抑制和边缘检测的效果明显优于其他方法。

[1]Raman M.Himanshu A.Study and comparison of various image edge detection techniques [J].International Journal of Image Processing, 2009, 3(1):1-11.

[2]Nadernejad E, Sharifzadeh S, Hassanpour H.edge detection techniques: evaluation and comparisons [J].Applied Mathematics Sciences, 2008, 2(31):1507-1520.

[3]Maini R.Analysis and development of image edge detection techniques [D].Punjabi University: College of Engineering, 2012.

[4]Canny J.A computational approach to edge detection[J].Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1986, PAMI-8(6): 679-698.

[5]Mallat S, Zhong S.Characterization of signals from multiscale edges [J].Pattern Analysis and Machine Intelligence, IEEE Transactions on, 1992, 14(7):710-732.

[6]王慧琴.小波分析与应用[M].北京: 北京邮电大学出版社, 2011: 178.

[7]Li Jun.A wavelet approach to edge detection [D].Sam Houston State University: The Department of Mathematics and Statistics, 2003.

[8]Zhang Zhen, Ma Siliang, Liu Hui, Gong Yuexin.An edge detection approach based on directional wavelet transform.Computers and mathematics with applications [J].Computers and Mathematics with Applications, 2008, 57(8): 1265-1271.

[9]Ma Weifeng, Deng Caixia.An improved wavelet multi-scale edge detection algorithm [C]//Wavelet Analysis and Pattern Recognition (ICWAPR), 2012 International Conference on, 2012: 302-306.

[10]Ricardo D.Adaptive edge-preserving image denoising using wavelet transforms [J].Pattern Analysis and Applications, 2013, 16(4): 567-580.

[11]Bai Jing, Zhou Huaji.Edge detection approach based on directionlet transform [C]//Multimedia Technology(ICMT), 2011 International Conference on, 2011:3512-3515.

[12]Pan Jianjia.Edge detection combining wavelet transform and Canny operator based on fusion rules[C]//Wavelet Analysis and Pattern Recognition, 2009.ICWAPR 2009.International Conference on, 2009:324-328.

[13]Al-Azzawi A K, Saripan M I, Jantan A, Rahmat R W O K.Edge detection innovator based on wavelet coefficients for images corrupted by the white-Gaussian noise [J].Scientific Research and Essays, 2011, 6(28):5951-5965.

[14]Workalemahu T.Singular value decomposition in image noise filtering and reconstruction [D].Georgia State University: College of Arts and Sciences, 2008.

[15]Hou Zujun.Adaptive singular value decomposition in wavelet domain for image denoising [J].Pattern Recognition, 2003, 36(8): 1747-1763.

[16]刘瑞祯, 谭铁牛.基于奇异值分解的数字图像水印方法[J].电子学报, 2001, 29(2): 168-171.

[17]Klema V, Laub A J.The singular value decomposition: Its computation and some applications [J].Automatic Control, IEEE Transactions on, 1980, 25(2): 164-176.

[18]Stewart G W.On the early history of the singular value decomposition [J].SIAM Review, 1992, 35(4): 551-566.

[19]Cang Y E, GuruPrasad M H.Robust edge detection for Swiss Ranger SR-3000 range image by singular value decomposition filtering and Hough transform [J].International Journal of Intelligent Control and Systems,2010, 15(4): 41-48.

[20]Takeda H, Farsiu S, Milanfar P.Kernel regression for image processing and reconstruction [J].IEEE Transactions on Image Processing: a Publication of the IEEE Signal Processing Society, 2007, 16(2): 349-366.

[21]Thaipanich T, Oh B T, Wu Pinghao, Xu Daru, Kuo C C J .Improved image denoising with adaptive nonlocal means(ANL-Means) algorithm [J].Consumer Electronics, IEEE Transactions on, 2010, 56(4): 2623- 2630.

[22]Andrews H C, Patterson C L.Singular value decompositions and digital image processing [J].IEEE Trans.on Acoustics, Speech and Signal Processing,1976, 24(1): 26-53.