燃气燃爆实验数据的多约束B样条曲线拟合

杨铮园， 申立勇

(中国科学院大学数学科学学院，北京101408)

数据点拟合在计算机辅助几何设计、计算机图形学和数控加工等领域都有广泛的应用，拟合中较常使用B样条曲线。B样条曲线具有较好的造型能力[1-2]。在拟合算法及提高精确度和效率方面，前人已做了许多研究。通常把平方距离和作为拟合误差，这样拟合过程就可以描述成一个求最小拟合误差的最优化问题。在优化迭代中，怎样估计拟合误差是一个关键的问题。目前已有很多估计拟合误差的方法，包括PDM，TDM，SDM，GTDM和CDM[3-4]等，在拟合效果和速度上都各有优缺点。Yang等[5]提出了隐式B样条曲线拟合算法，适用于更一般的情形，比如几条分离的闭曲线的拟合。Flöry[6]提出了在障碍存在下的B样条曲线曲面拟合算法，该算法能够进行点云边界的重构，并推广到避开一般真实障碍物的曲线曲面重构。本文针对实际实验数据，采用多约束条件下的样条拟合，处理油气爆炸界限的估计问题，得到不同氧气浓度下油气浓度和爆炸强度曲线，应用于燃爆预判。

近年来，工业生产过程危险化学品事故频繁发生，事故造成了生命和财产的重大损失。因此，危险化学品事故的预测是众多学者积极研究的主题[7-9]。Chang和Lin[10]整理了在2006年之前的40年间有记载的工厂事故，其中约74%的事故发生在石油精炼厂、石油港口和油库。近年来这类事故的数量还在上升，包括2010年大连港油库爆炸事故。油罐爆炸可能会导致多米诺骨牌效应，加剧意外事故所造成的损害[11]。油罐爆炸主要是油气燃爆引起的，因此对油气爆炸范围进行分析非常必要，良好的分析结果将有助于防止油气爆炸事故的发生。之前人们主要应用不同分类器对某种油气的实验数据进行分析，通过训练得到合适的分类器参数，从而可以对新数据进行是否属于可以燃爆范围的预判。常用的分离器包括支持向量机(SVM)方法[12]、逻辑回归(LR)方法[13]等。这类基于统计分析的分类器一般适合给出逻辑变量分类，即是否可燃爆。例如目前常用的燃气容积比作为因变量，而它的可燃性作为目标变量。但是实际生产中人们不仅关注燃气是否爆炸，还关注其爆炸程度强弱，以便对后援工作进行有效安排。因此，本文基于此实际需求，对某油罐燃气可燃性以及燃爆强度进行分析，其影响因素涉及其中的油气浓度和氧气浓度等。我们通过在特制的密闭管道内进行油气爆炸试验，从而获取在常温常压条件下不同油气浓度、氧气浓度预混气体的爆炸极限及爆炸强度值(图1)。然后分析不同氧气浓度下的油气燃爆界，以及可燃爆情况下的爆炸强度。

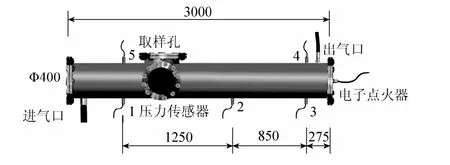
图1 实验装置示意图(单位：mm)

本文在关注油气数据拟合中，首先根据问题的物理化学背景和实验数据特征，对拟合曲线的预期性质进行估计。然后把这些性质转化为曲线拟合中的约束条件，对拟合曲线进行带约束的优化。包括，不同氧气浓度下的爆炸强度曲线应该互不相交；爆炸强度曲线是凸曲线；爆炸强度曲线应该为安全曲线等。这些要求在转化为约束条件时又有不同的转化和实现方式，需要不同的尝试。本文首先回顾了B样条曲线拟合的一般过程、SDM误差项估计方法和Flöry的障碍约束方法，然后根据数据特征和问题背景导出曲线组拟合的约束条件，最后在实际实验数据上实现算法，在分析、比较拟合效果后选择合适的方案。

1 实验数据和样条拟合

1.1 实验数据采集

在实验装置中(图1)，首先测量实验油气(HC)浓度、氧气(O2)浓度和惰性气体(CO2)浓度，惰性气体主要是用来调整前两种实验气体浓度。然后通过点火装置，再由传感器测量并记录引爆后的各自气体浓度，包括油气、氧气、一氧化碳、二氧化碳。在3个位置安装了浓度传感器，将数据平均值作为最终实验数据进行分析。另外，还安装了5个压强传感器，测量爆炸瞬间的压强，其平均值作为实验压强值，该瞬时压强称之为燃气爆炸强度。而燃气燃爆界是指固定氧气浓度下油气发生爆炸的浓度边界，通常用上下界区间表示。表1和表2分别给出了引爆后发生爆炸和没有爆炸的两组实验数据；表3为爆炸瞬间压强表。

整个实验过程中，共采集、整理了44组数据(图2)。经初步分析发现，随着氧气浓度的增大，油气爆炸范围增大、爆炸强度也增强。因此，将数据按氧气浓度分类，然后对每一组数据进行拟合。但是每组数据拟合不是独立的，不同氧气浓度下爆炸曲线有相互约束关系。

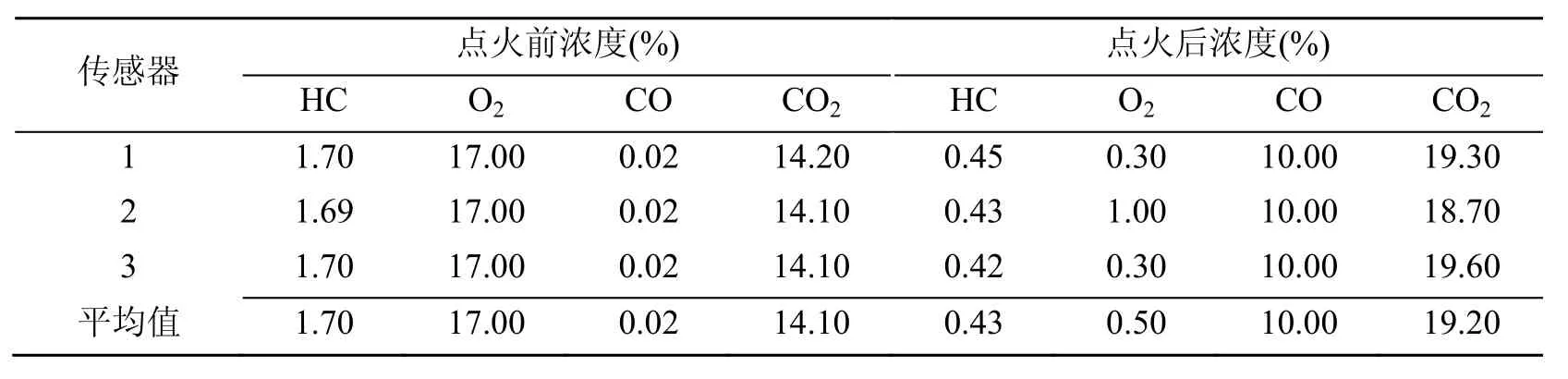
表1 爆炸实验数据(No.21)

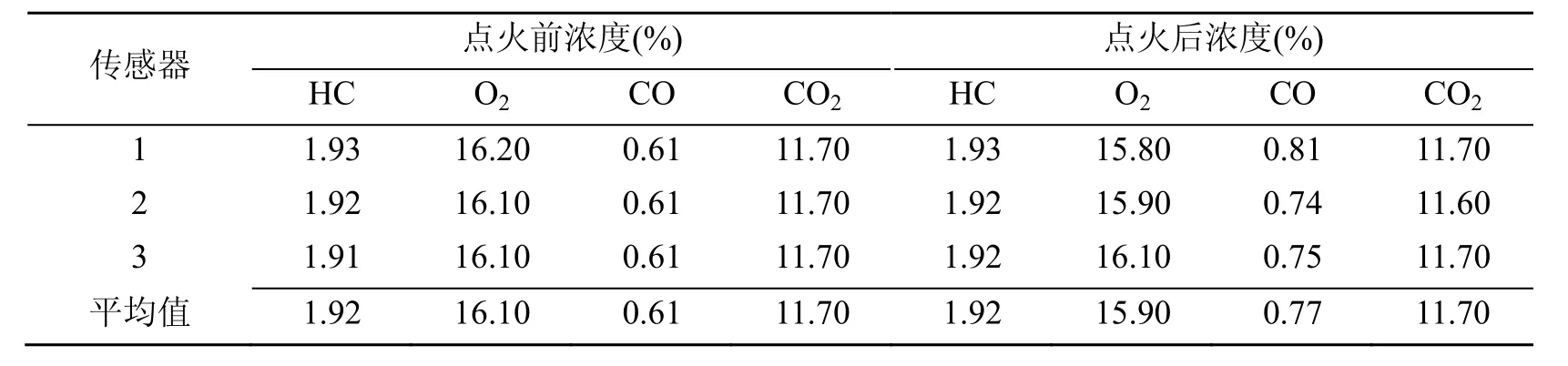
表2 未爆炸实验数据(No.19)

表3 爆炸瞬间压强(MPa)

图2 实验数据

1.2 B样条曲线拟合

设f:ℝ→ℝ2:t↦f(t)是平面上的一条参数曲线。已知有n个控制点的B样条曲线的一般表示为：

其中，Bk,i(t)∈ℝ是k次B样条基函数，是曲线的控制点。令：

则式(1)可以写成矩阵表示：

给出平面上的一组无序数据点pk,k=1,…,m，用一条B样条曲线来拟合这些点，使得这条曲线尽可能地描述这些点的轨迹形状。这一过程可以描述为如下一个非线性优化问题：已知点集求一组控制点c,i=1,…,n,∈ℝ2，使i得目标函数：

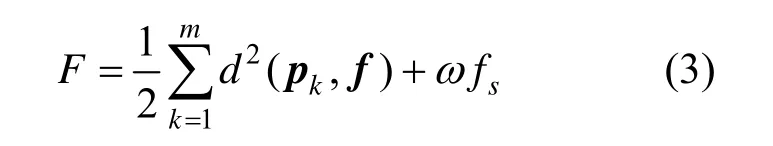
的值最小。其中|d(pk,f)|是pk到曲线f(t)的距离，ωfs是平滑项。

式(3)的最优化问题可以用迭代过程解决。我们不妨设f(tk)是已知曲线f(t)上距离pk最近的点，pk到曲线f(t)的距离定义为|d(pk,f(tk))|。对控制点向量C做位移为δC的扰动，则原始曲线f(t)变为：

pk到曲线的距离未知，但是可以用合理的方法来估计。优化问题的关键在于如何估计曲线的拟合误差d2(pk,）。Wang等[3]提出的SDM方法给出的误差项：

其中，Tk和Nk分别是f(tk)点的单位切向量和单位法向量，ρk是f(tk)点的曲率半径。|dk|=||pk-f(tk)||，当ρk与曲率中心K在曲线f(t)同侧时dk＞0，异侧时dk＜0。显然dk＜ρk。式(5)可展开计算并求和，

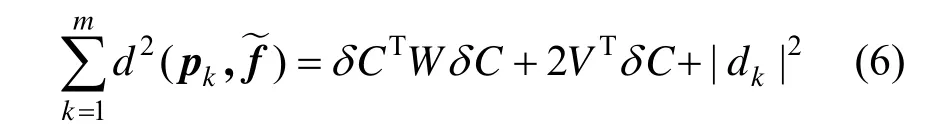
其中：

另一方面，平滑项部分在实际应用中常用最小化薄板能量，使用二阶导数的平方[14]，因此fs也是C的二次函数：

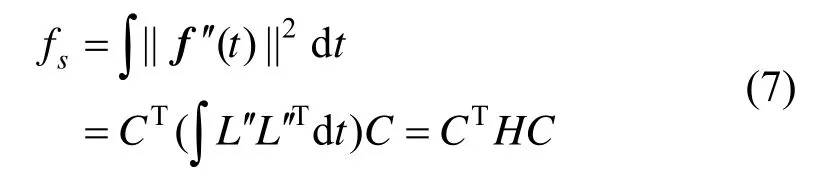
于是式(3)的无约束最优化问题等价于在现有值C的情况下，每次迭代中最小化如下函数：

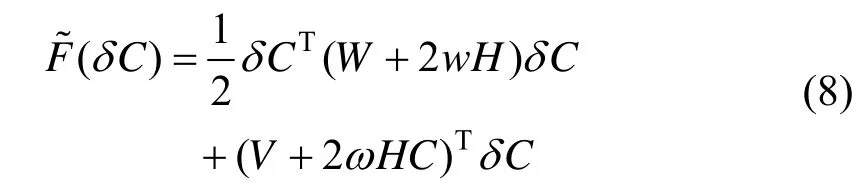
根据以上记号，B样条曲线拟合算法可描述如下：

输入：需要拟合的一组二维无序数据点pk,k=1,…,m,∈ℝ2。

输出：一条B样条拟合曲线f(t)。

(1) 根据所要拟合的数据点，合理设置初始控制点,i=1,…,n，根据式(2)计算出初始的B样条曲线f0(t)。

(2) 对每个数据点pk，计算其在当前的曲线fr(t)上的最近点fr(tk)。

(3) 通过求解式(8)的最小值，计算拟合曲线控制点Cr的位移δCr。则新的拟合曲线为fr+1(t)=LT(t)(Cr+δCr)。如果新的拟合曲线满足了事先设定的条件（比如迭代步数或者误差阈值的控制），则转到第4步；否则转到第2步。

(4) 输出拟合曲线fr+1(t)。

在样条拟合的一般算法的基础上，Flöry[6]提出了在一般障碍物存在的情况下拟合点云的方法。

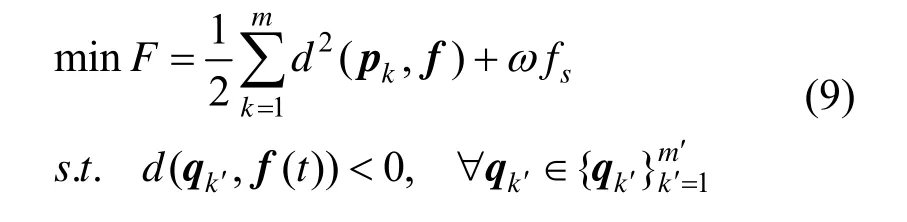
同上文类似的记号，并记f()处的向外单位法向量n)，则式(9)的约束等价于：

由于每个数据点对应的与当前的拟合曲线的控制点相关，故可写成f(t)的控制点向量C的函数，并记式(10)左侧的线性近似为′(C)，则：

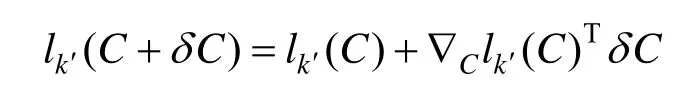
因此，约束(10)可以近似写成：

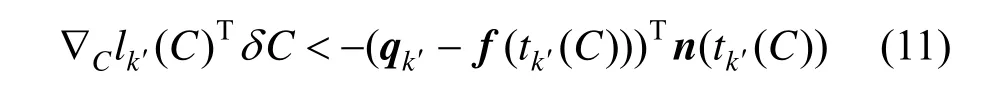
′(C)对每个控制点ci求偏导：

其中，I是二阶单位矩阵，J是将切向量向曲线外旋转π/2的矩阵。经整理后可写出梯度矩阵∇Clk′(C)，式(12)的具体推导过程可参见文献[6]。

2 多约束的B样条曲线拟合

根据爆炸数据的物理化学特征，将不同的拟合约束转化为合理的数学条件，并对条件做进一步简化。

2.1 多条互不相交的曲线拟合

爆炸反应的原理显示，在相同的油气浓度下，爆炸强度的大小跟氧气浓度有关。不同氧气浓度下的爆炸强度曲线应该互不相交。因此在实际应用于爆炸数据的拟合中，需要针对曲线性质的特殊要求，对拟合曲线进行带约束的优化。对于本文的实验数据，不能直接应用上一节的方法。因为Flöry的算法处理的障碍物都是处于静止状态下，拟合的多条曲线分别作为其他曲线的边界约束在每一次迭代中会发生变化，因此约束曲线上取的样点作为障碍点也在变化。

上述问题的拟合可以用两种方法来完成。首先很直接地想到第一种方法：先拟合其中一条曲线，比如f2(t2)，然后拟合另一条曲线f1(t1)时，在f2(t2)上取足够多的样点作为障碍点集，即可用上一节的带约束的算法来拟合f1(t1)。这样的做法能够满足曲线互不相交，但是曲线拟合顺序的不同可能导致产生不同的拟合效果，尤其在两组点云重叠部分会有明显的偏差，较先拟合的曲线对拟合结果的影响较大。

第二种方法旨在解决第一种方法中可能出现的问题，避免因曲线拟合的顺序不同产生较大的偏差，对{p1,k1}和{p2,k2}同时进行拟合。把两个控制点向量C1和C2写成一个列向量，第r步迭代中，在当前曲线f2(t2)上取足够多的样点f2(t2,k′),k′=1,…,m′。下一步迭代中由于曲线f2(t2)的变化，f2(t2,k′)也随之移动，记为(t2,k′)，要求(t2,k′)都在(t1)的内侧。于是可转化为解问题：

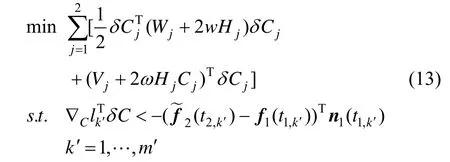
记号定义同上文。曲线f2(t2)上的样点f2(t2,k′)可以写成C2的函数，故是C1和C2的函数。对属于C1的控制点的偏导可参照式(12)，对属于C2的控制点c2,i的偏导：

B2,i(t2)是f2(t2)的B样条基函数。于是式(13)的约束可写成：

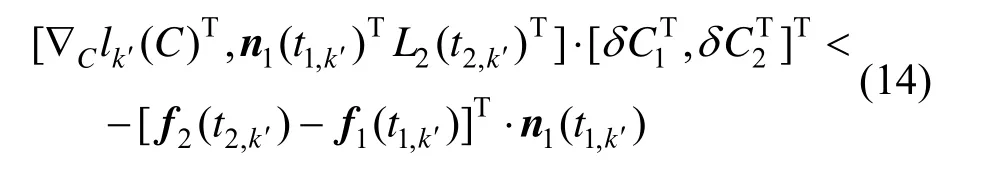
多组数据的相互约束拟合可基于上述两组数据拟合的约束条件。lk对不与当前拟合曲线有边界约束关系的曲线的控制点的偏导均为0，因此整理后也可写成如(14)的线性不等式约束。

2.2 凸曲线的拟合

根据燃气爆炸实验的特点，在氧气浓度固定的情况下，油气浓度达到爆炸区间的某一值时，爆炸强度可达到最大，爆炸强度曲线应是凸曲线。在上一小节的的约束拟合中加入新的约束用以保证拟合曲线的上凸性质。不妨设拟合函数f(t)需要保持向外凸的性质，故在曲线的任一点处的曲率中心均在曲线的内侧。这一条件也可叙述为f′′(t)始终与f(t)的向内法向量同向。沿用上文的记号，J是将f′(t)向曲线外旋转π/2的矩阵，则JT是将f′(t)向曲线内旋转π/2的矩阵。曲线f(t)=L(t)TC应满足：

写成控制点向量C的约束：

上式的左侧发生扰动δC后在C处展开并线性化：

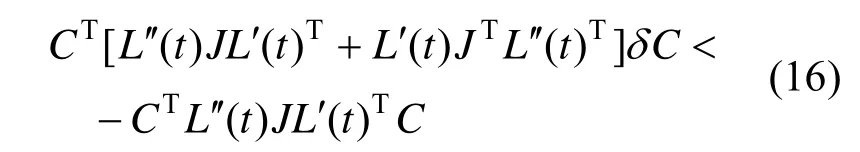
式(16)就是保持拟合曲线外凸性质的约束条件。在实际应用中，可以在每一次迭代中在f(t)上取足够多的样点，用式(16)的约束求解子问题的最优化问题。

上述条件实现中，算法需要在f(t)上取足够多的样点，因此存在如何控制所取样点数目的问题。下面我们根据样条的变差缩减性质直接给出控制点约束，从而导出线性的简化条件。设拟合函数f(t)是外凸，由B样条曲线变差缩减性，曲线的凸性受控于其控制多边形凸性。如前文，J是将向曲线外旋转π/2的矩阵，则JT=-J是向曲线内旋转π/2的矩阵。外凸曲线f(t)应满足：

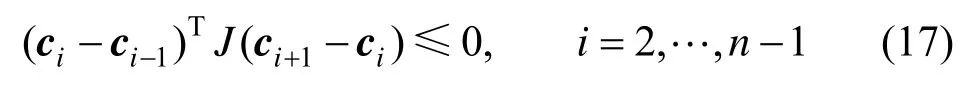
上式的左侧发生扰动δC后在C处展开并线性近似，设ai=ci+1-ci,i=1,…,n-1，整理后得：

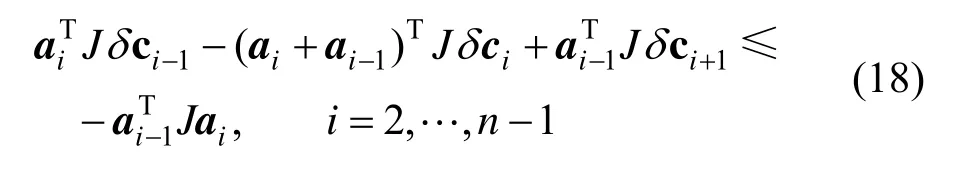
式(18)就是用变差缩减性质保证曲线外凸的约束条件，只使用了控制点之间的关系，比直接用曲线上点的曲率构成的式(16)简单得多。

2.3 外边界约束的曲线拟合

油气爆炸曲线拟合的目的在于对有爆炸危险的浓度预警，在应用中可能出现两种错误：一种是可燃爆数据被判定为安全；另一种则是不可燃爆数据被判定为可燃爆。在实际生产中，前一种错误显然更加危险，一旦诱发燃爆，带来的损失将远远大于后一种错误。因此，爆炸强度曲线应为安全曲线，即至少保证安全曲线之外没有任何燃爆数据点。另一方面，还需考虑预警的准确性，即希望拟合曲线尽量靠近实验数据。综合两个要求，需对爆炸数据作外边界拟合。对于每一组数据的拟合曲线，把这组数据作为障碍点约束用于拟合数据点的外边界。数据点的边界拟合是Flöry算法的一种特殊情形，通过设置d(pk,f(t))＜0或d(pk,f(t))＞0即可拟合出的外边界或内边界。约束条件应为：

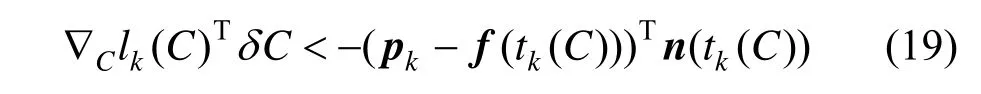
3 数据拟合结果与分析

通过油气爆炸实验中获取了四组数据点，分别记为{p20},{p18},{p16},{p15}，表示实验反应在氧气浓度为20%、18%、16%、15%采集到的爆炸压强。用横坐标表示爆炸反应前气体中油气的浓度，纵坐标表示爆炸时测得的平均压强，需要用四条B样条曲线f20(t),f18(t),f16(t),f15(t)分别拟合这四组爆炸数据。首先用B样条曲线拟合的一般方法分别拟合四组数据点，可以粗略地看一下爆炸曲线的走势，得到的拟合结果如图3。

图3 一般B样条拟合

从图3可以看出，曲线无凸性且两条曲线有交点，不符合燃气燃爆特性。依据曲线不相交约束的拟合算法，使用第一种方法，先对其中一组数据点做曲线拟合，然后对其他数据点分别做拟合时，在已拟合好的曲线上取若干点作为边界约束。用第一种方法得到自上而下的约束拟合图4(a)和自下而上的约束拟合图4(b)，相应的曲线拟合优先顺序分别是f20(t)＞f18(t)＞f16(t)＞f15(t)和f15(t)＞f16(t)＞f18(t)＞f20(t)。从图中可以看出，由于曲线拟合顺序的不同，图4(a)和图4(b)有不同的拟合效果，这里较明显的不同表现在曲线f18(t)和f16(t)上。与图3没有约束情况下的拟合结果相比，显然在图4(a)中，f18(t)和图3中相应的曲线形状大致相同，而f16(t)则因为f18(t)的限制而有明显的变化，在图4(b)中则相反。这一结果验证了先拟合的曲线对整体拟合结果影响较大，而后拟合的曲线对先拟合的曲线没有约束效果。

图4 带边界约束的爆炸数据拟合

用第二种方法，式(14)，四条拟合曲线相互约束，互为上/下边界，拟合结果如图5。与图4(a)和图4(b)的按顺序分别拟合的效果相比，图5的相互拟合在直观上有折中的效果，尤其在f18(t)和f16(t)上表现得比较明显。从原理上来说，实验测得的数据由于一些未知原因产生误差，因此不能确定哪一组数据比较准确或者靠近理论值。如果较先拟合的数据不准确，那么整体的拟合效果就会受到较大的影响。因此，采用第二种方法将曲线彼此作为约束条件能够较好地平衡这种关系，减小由于测量误差导致的拟合误差的增大。

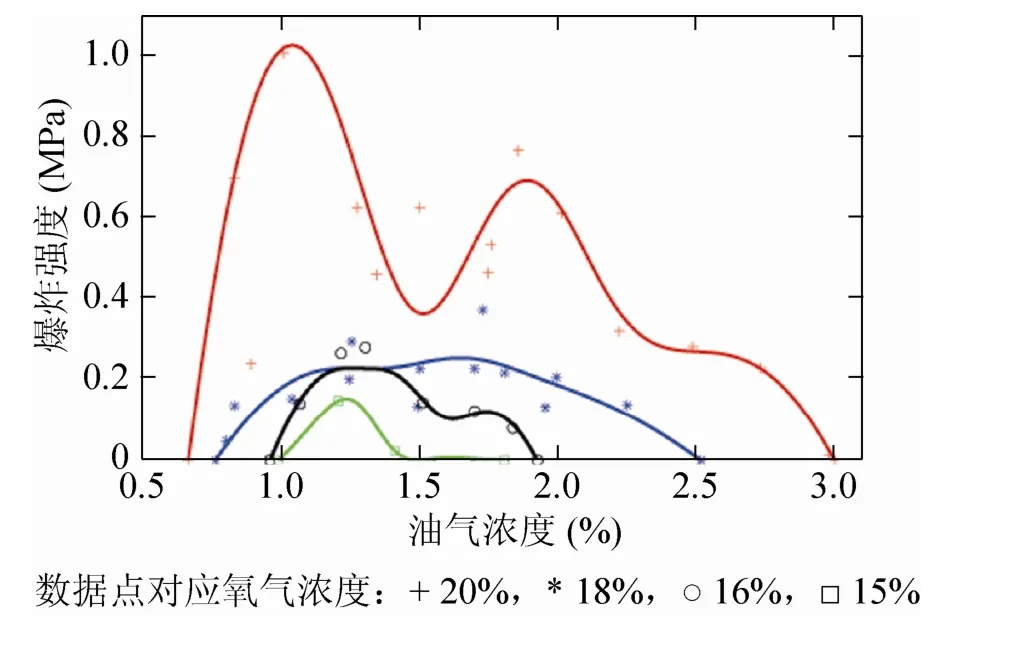
图5 互为边界约束的爆炸数据拟合

从理论上看，固定氧气的浓度，实验爆炸时的压强对于油气的浓度作图会呈现上凸的形状。前面的拟合曲线都呈现出波动的状态，要避免这种波动可以加上上凸曲线的约束。如果只用式(18)的约束来做拟合，得到图6(a)，与图3类似，曲线之间有交点。图6(b)在式(18)的基础上加上式(14)，更加符合理论上对爆炸压强拟合曲线走向的预期。

为了得到爆炸强度的安全曲线，我们对四组数据点做相互约束的外边界拟合，得到图7(a)，直观上是将爆炸点都包在曲线内部。但如前讨论，曲线呈现出不合理波动状态。加上了上凸约束之后的图7(b)与图6(b)相比，图7(b)的爆炸强度曲线形状相似度更高一些。综合考虑到拟合曲线的准确性、曲线形状与真实情况的比较、以及危险预警的安全性，图7(b)是本文推荐的爆炸强度曲线的拟合结果，当氧气浓度为15%、16%、18%、20%时，其对应的油气燃爆界限分别为[0.98,1.81]、[0.95,1.91]、[0.75,2.53]、[0.72,3.02]。值得注意的是，具有凸性的安全曲线之间没有交点，因此这组实验数据拟合中，不必添加互为边界的约束。

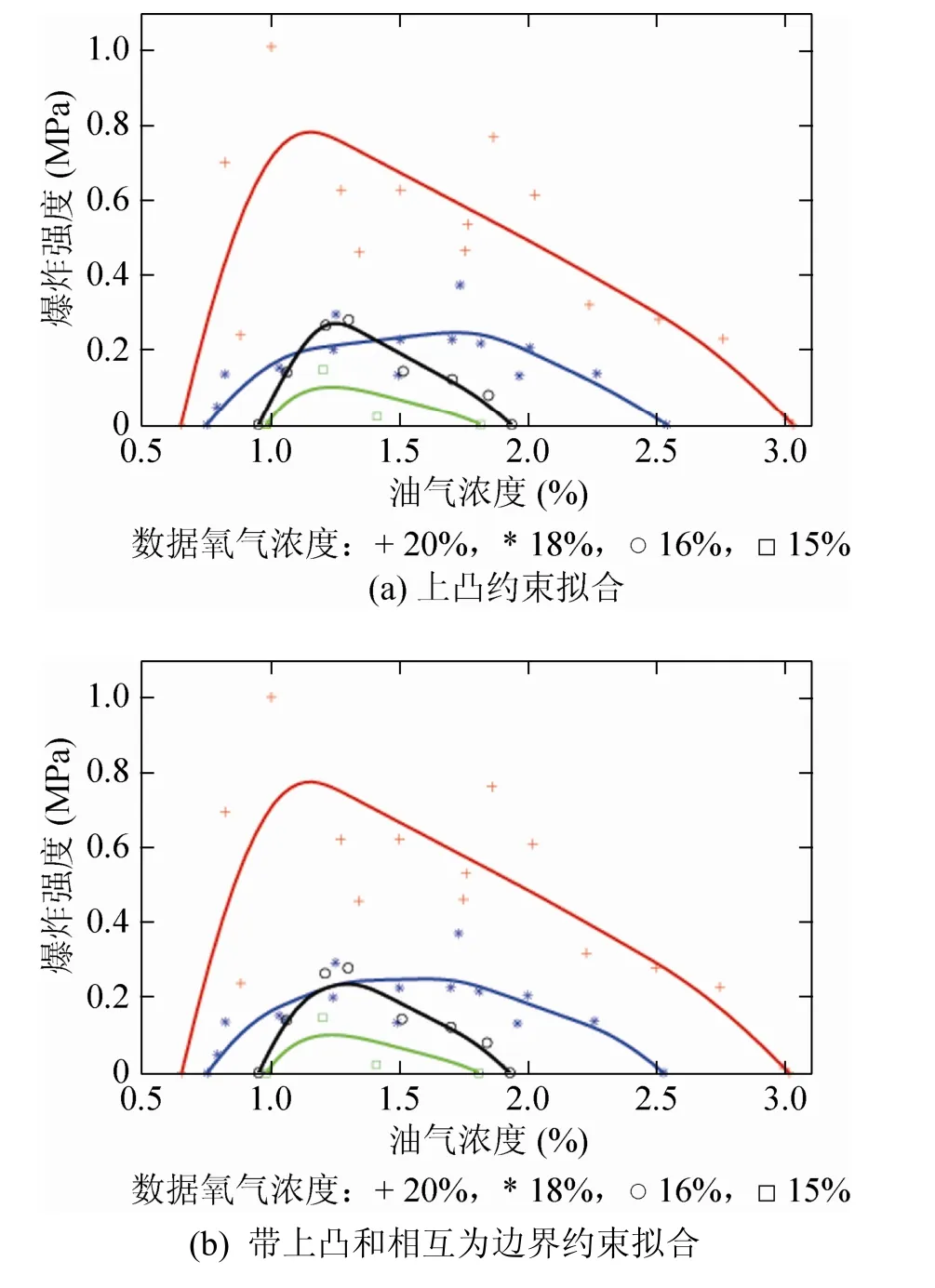
图6 上凸约束的爆炸数据拟合

图7 爆炸强度的安全曲线拟合

4 结束语

本文针对某燃气燃爆实验数据，给出了多约束条件样条拟合的一个应用实例。该实例本质上是给定数据的多条件曲线拟合问题，本文主要在于约束条件数学化、条件合理简化以及拟合算法的实现。经过分析和比较，我们选择具有上凸性质的安全曲线拟合为最终分析方案。拟合得到安全曲线和爆炸界限都比较合理，并且得到合作消防公司的认可。更为重要的是，该方法可以推广到多因素燃爆模型。实际工程生产中，燃爆影响因素除了本文涉及的各种混合气体浓度和压强，还可以有温度、湿度等。添加新的影响因素，在我们的分析方法中转化为增加样条拟合维数，即多约束曲线拟合转化为(超)曲面拟合。

[1]Pottmann H,Leopoldseder S,Hofer M.Approximation with active B-spline curves and surfaces [C]//10th Pacific Conference on Computer Graphics and Applications,Proceedings,2002: 8-25.

[2]Shen Liyong.Error Bounded Conic Spline Approximation for NC Code [C]//Proc.of International Conference on Machine Vision (ICMV2011),SPIE 8349,2011: 1-7.

[3]Wang Wenping,Pottman H,Liu Yang.Fitting B-spline curves to point clouds by curvature-based squared distance minimization [J].ACM Transactions on Graphic,2006,25(2): 214-238.

[4]Liu Yang,Wang Wenping.A revisit to least squares orthogonal distance fitting of parametric curves and surfaces [J].Lecture Notes Computer Science,2008,4975: 384-397.

[5]Yang Zhouwang,Deng Jiansong,Chen Falai.Fitting unorganized point clouds with active implicit B-spline curves [J].The Visual Computer,2005,21(8-10):831-839.

[6]Flöry S.Fitting curves and surfaces to point clouds in the presence of obstacles [J].Computer Aided Geometric Design,2009,26(2): 192-202.

[7]Rasbash D.Review of explosion and fire hazard of liquefied petroleum gas [J].Fire Safety Journal,1980,2:223-236.

[8]Bakke J R,Van Wingerden K,Hoorelbeke P,Brewerton B.A study on the effect of trees on gas explosions [J].Journal of Loss Prevention in the Process Industries,2010,23(6): 878-884.

[9]Cheng Jianwei,Yang Shengqiang.Improved coward explosive triangle for determining explosibility of mixture gas [J].Process Safety and Environmental Protection,2011,89(2): 89-94.

[10]Chang J I,Lin Chengchung.A study of storage tank accidents [J].Journal of Loss Prevention in the Process Industries,2006,19: 51-59.

[11]CCPS.Guidelines for Chemical Process Quantitative Risk Analysis [M].2nd ed.Wiley-AIChE,1999: 57-283.

[12]Vapnik V.The Nature of Statistical Learning Theory [M].NY,Springer,1999: 137-170.

[13]王济川,郭志刚.Logistic回归模型——方法与应用[M].北京: 高等教育出版社,2001: 146-181.

[14]Brunnet G,Hagen H,Santarelli P.Variational design of curves and surfaces [J].Surveys on Mathematics for Indestry,1993,3: 1-27.