无失效数据情形可靠性参数的分析
2014-03-28罗学刚任占勇武月琴
罗学刚 任占勇 武月琴 王 欣
(中航工业综合技术研究所,北京 100028)
目前在航空装备的可靠性鉴定试验中,一般采用GJB 899A-2009《可靠性鉴定和验收试验》的试验统计方案和可靠性参数评估方法。试验中获得的数据经常是各种截尾数据。在定时截尾试验中,如果失效(或故障)数大于零,对由这种试验方式获得的数据(称为有失效数据)进行可靠性研究,己有相对比较成熟的方法。但由于科学技术的进步,高可靠性产品迅速发展,在定时截尾试验中获得的数据有时是“无失效数据”,即在规定的试验时间内没有产品失效。
对于有失效数据的情形,GJB 899A-2009给出了可靠性参数的评估方法。在无失效数据情形下,如何对产品进行可靠性统计分析,对于建立在失效数据分析基础上的可靠性理论来说,是一个有一定难度的问题。寻找在无失效数据条件下进行科学、有效的可靠性分析方法,现已成为可靠性研究中一个新的而又十分重要的领域。本文对故障前工作时间服从指数分布的产品,介绍了目前最优置信限法、卡方分布的分位点法、修正似然函数法、配分布曲线法、参数的综合估计法等无失效数据情形下的可靠性评估方法,对上述方法的特点及工程适用性进行了分析,证明了最优置信限法与卡方分布的分位点法结果的一致性。
1 无失效数据可靠性评估
设产品的寿命服从指数分布,其密度函数为:

λ为产品的失效率。
设对故障前工作时间服从指数分布的产品进行了m次定时截尾试验,截尾时间分别为ti,i=1,2,…,m,且在ti处有ni个产品进行定时截尾试验,所有样品无一失效,获得的无失效数据为(ti,ni),i=1,2,…,m。下面分别用不同的方法评估产品的可靠性。
1.1 最优置信限法
根据产品的无失效数据为(ti,ni),i=1,2,…,m,最优置信限法给出的产品的平均故障间隔时间(MTBF)在置信水平为1–α时的置信下限为:
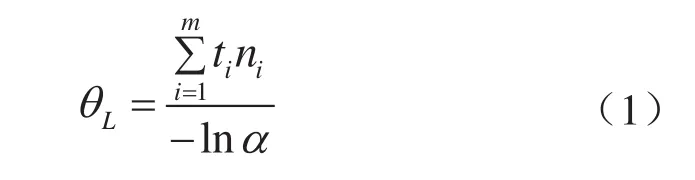
陈家鼎等首先对ni=1的情形得到上述的结果[1],i=1,2,…,m。韩明在指数分布情形方面推广了陈家鼎等的无失效数据情形下可靠性参数的最优置信限法[2],研究了在定时截尾试验中,在各截尾时刻试验样品数分别为ni的情况,并得到公式(1)。若令,则公式(1)可写为:

1.2 卡方分布的分位点法
戴树森在定时截尾试验总试验时间为T,失效次数为零时给出了MTBF在置信水平为1–α时的置信下限为[3]:

1.3 修正似然函数法
王玲玲等提出了无失效数据的统计分析方法──修正似然函数法[4]。根据修正似然函数,得到了产品MTBF的修正极大似然估计为:


其中α=0.7,0.6,0.5,这3个值得到的MTBF的修正极大似然估计,α越小得到的结果越保守。
1.4 配分布曲线法
配分布曲线法,其基本思想是:先估计失效概率,然后用最小二乘法给出分布参数的估计,最后给出可靠度的估计。其具体步骤如下:
1)在截尾时间ti处(i=1,2,…,m)获得失效概率的估计,其中T为产品的寿命;
2)通过诸点(ti,)(i=1,2,…,m)配一条分布曲线,这相当于在分布曲线族中选一条曲线最靠近诸点(ti,),这里靠近的标准选用最小二乘的标准;
3)由确定下来的分布曲线求得可靠性参数的估计。
1.5 可靠性参数的综合估计法
利用产品的无失效数据为(ti,ni),i=1,2,…,m 得到失效率的最小二乘估计为:
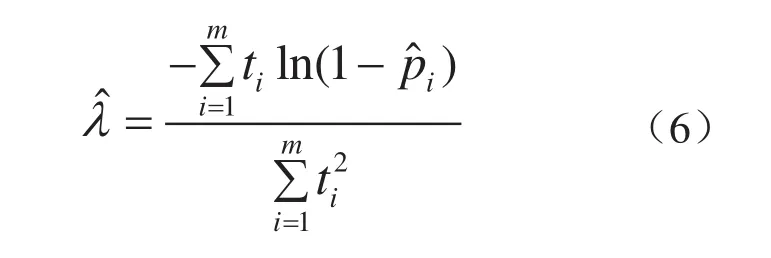
2 可靠性评估方法的分析与比较
上面给出了5种常用的在无失效数据情形下产品可靠性的评估方法,如何评价一种评估方法的好坏是一个新的问题。下面对这些评估方法进行分析与比较,配分布曲线法适用于截尾次数较多的情况;可靠性参数的综合估计法要用到Bayes方法,先验分布的选择直接影响评估结果;修正似然函数法得到是可靠性参数的点估计,其实就是产品平均故障间隔时间的置信度为0.7(0.6或0.5)时的置信下限。当两种方法给出的是同一置信度下可靠性参数的下限估计时,则下限越大越好。为了比较最优置信限法及卡方分布的分位点法,我们首先证明下述引理。

证明:服从自由度为n的χ2分布的随机变量的密度函数为,即此随机变量的分布函数为形状参数为n/2,尺度参数为1/2的gamma分布,因此随机变量的密度函数为:

当n=2时,可以得到服从自由度为2的χ2分布的随机变量的密度函数为:
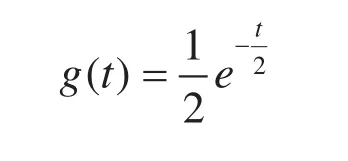
根据分位数的定义有:

即
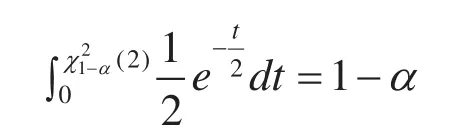
化简得:
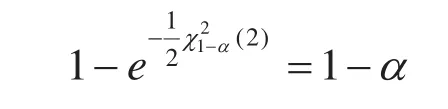
即
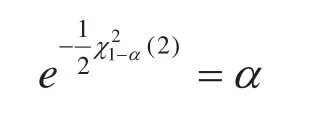
两边取对数得:
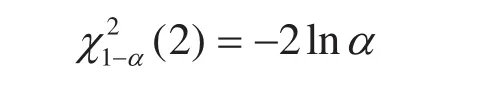
根据引理可得
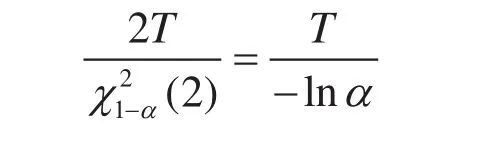
因此可知根据最优置信限法与根据卡方分布的分位点法得到的产品MTBF的置信下限是相同的。
在美国国防部指令性文件DoD 3235.1-H《系统可靠性、可用性和维修性试验和评估入门》中给出了在失效次数r≠0时,产品的MTBF在置信水平为1–α时的置信下限为:

[1] 陈家鼎,孙万龙,李补喜. 关于无失效数据情形下的置信限[J].应用数学学报. 1995,18(1): 90-100.
[2] 韩明.无失效数据情形可靠性参数的置信限[J].工程数学学报. 2004,21(2):245-249.
[3] 戴树森.关于寿命试验的某些统计分析[J].数学的实践与认识. 1982,3:47-60.
[4] 王玲玲,王炳兴.无失效数据的统计分析一修正似然函数方法[J].数理统计与应用概率. 1996,11(1):64-70.
[5] 韩明.无失效数据可靠性参数的综合估计[J].数学理论与应用. 2000, 20(3):36-44.
