基于GA-BP 神经网络的粮仓通风控制研究

孙彪瑞，廉飞宇，王 珂，苏庭奕，赵中原，张 元

（河南工业大学 信息科学与工程学院，河南 郑州 450001）

0 引言

如何控制和减少粮食产后损失、保障国家粮食安全，是我国粮食行业致力解决的重要问题，而针对实际粮情，实现科学有效的粮仓通风管理是减少粮食仓储损耗的重要方法之一.机械通风技术是目前国内外应用最广泛的粮食储藏技术之一[1].而在大多数的粮库机械通风控制中采用的都是基于专家系统的通风决策控制，专家系统虽然具有符号知识处理能力、提供领域专家级的指导服务等优点，但也存在领域知识获取困难、容错能力差、处理偏离知识领域的问题时性能将急剧下降等缺点[2].随着信息化技术向社会各个领域的渗透和扩展，粮食行业也提出了信息化的要求，继而粮食仓储智能通风的概念[3]被提了出来.目前已经有很多学者和团体在研究智能化的粮仓通风控制系统且已有了相应的成果[4-6]，然而许多智能通风控制系统只是在结合了粮情测控系统[7]的基础上实现了粮仓通风设备的自动控制，也就是说对通风决策方案的研究还不够深入，智能化程度还不够高.在粮仓智能通风控制系统中，通风决策方案的选择直接决定智能通风控制系统的好坏，所以寻求一种准确、高效的通风决策方法是很有必要的.

BP（Error Back Propagation）神经网络又称误差反向传播神经网络，是诸多神经网络模型中应用最广泛的一种，也是解决非线性问题的有力工具，它将信息全部存储于网络的连接权系数中，使网络具有一定的泛化能力和容错性.BP 神经网络可以将多种粮情信息进行融合处理，从而给出更加真实可靠的通风决策结果.但传统的BP 算法采用的是梯度下降法，收敛速度较慢，训练时也易陷入局部极小值.而遗传算法（Genetic Algorithm，GA）是一种自适应启发式全局搜索算法，它仿效生物的进化和遗传，根据适者生存和优胜劣汰的进化原则，不断得到更优的群体，同时以全局并行搜索的方式来搜索优化群体中的最优个体，使待解决的问题一步一步逼近最优解或近似最优解.

作者在传统BP 神经网络的基础上，利用GA对BP 神经网络的连接权值和阈值进行优化并进行二次寻优，建立GA-BP 神经网络通风控制模型，利用GA 全局搜索能力摆脱了传统BP 神经网络收敛速度慢和易陷入局部极小值的缺点.GABP 神经网络应用于粮仓通风控制中，可以根据粮情测控系统采集到的实时粮情数据对通风模式做智能化的决策，这就为粮仓通风决策又提供了一种高效、可靠的方法，提高了智能通风控制系统的智能化程度.

1 理论分析与模型建立

1.1 BP 神经网络

BP 神经网络是典型的有监督学习型前馈神经网络，它由输入层、隐含层和输出层组成，隐含层可以由一层或多层组成.Kolmogorov 定理[8]指出，包含一个隐含层的3 层BP 神经网络在闭集上可以以任意精度逼近任意连续函数.所以，作者采用简单的3 层BP 神经网络建立模型，其网络结构如图1 所示.

图1 3 层BP 神经网络的网络结构

在图1 中，x1，x2，…，xN为神经网络的输入变量；y1，y2，…，yM为网络输出值；ωij和νjk分别为输入层与隐含层、隐含层与输出层的连接权系数；αj和βk分别为隐含层和输出层各神经元的阈值，j=1，2，…，L；k=1，2，…，M；N、L、M 分别为输入层、隐含层和输出层神经元的个数.设X=（x1，x2，…，xn）T，Y=（y1，y2，…，ym）T，则神经网络就建立了从X到Y 的一种函数映射关系，实现了从N 维空间到M 维空间的非线性映射.对于这3 层BP 神经网络，输入输出函数关系为：

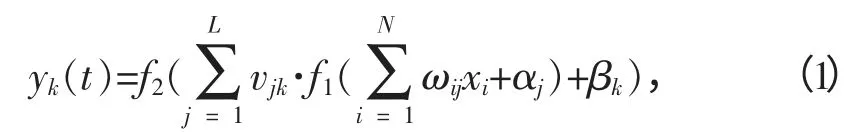
式中:f1（x）为隐含层神经元激活函数；f2（x）为输出层神经元激活函数；t 表示网络训练次数.

建立BP 神经网络时需要考虑的一个重要因素就是神经元激活函数f 的选取，常用的激活函数有阶跃型、线性和Sigmoid 函数等.为了便于输出结果和实际通风模式的编码映射，再结合各激活函数的性质，隐含层和输出层均选择Sigmoid 函数作为神经元的激活函数.另外，在BP 神经网络模型的建立过程中，隐含层神经元的个数确定是一件十分重要的事情，如果隐含层神经元的个数取得太少，就会因为网络无法获取到足够的信息而使问题无法得到解决；如果神经元个数太多又容易引起“过度拟合”现象，而且还会大大增加网络的训练时间.目前，神经网络隐含层神经元个数的选取还缺乏有力的理论知识作指导，大多是针对特定问题基于经验的选取.作者采用经验公式来选取隐含层神经元个数[9]：

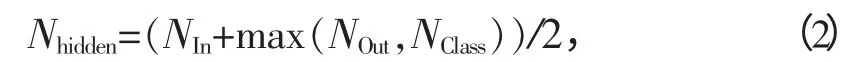
式中:Nhidden为隐含层节点数；NIn、NOut、NClass分别为神经网络的输入层节点数、输出层节点数和所需分的目标分类数;max（x，y）为求最大值的函数.

相对于隐含层，输入层和输出层的神经元个数的选取相对比较固定.对于一般的3 层BP 神经网络，输入层的神经元个数一般取为神经网络输入特征向量的维数，而输出层神经元个数取为目标结果（类别）数.

1.2 遗传算法

GA 是一种模拟生物进化论和自然选择的计算模型，它采用了全局搜索技术，把种群看作是一组问题的解，通过对当前种群施加复制、交叉和变异等遗传操作，并在每一代中利用适应度函数来决定遗传到下一代的种群个体，产生新一代的种群.依次循环下去，进化的末代种群将包含近似最优解.与生物的进化过程类似，GA 对变量集合的编码进行处理而非变量本身，是直接对结构对象的操作，不存在函数连续性和求导的限制.且GA 具有内在的隐并行性和更好的全局寻优能力，直接以适应度函数作为搜索条件，运用概率化寻优方法，可以自动获取和指导优化的搜索空间，自适应调整搜索的方向，不需要确切的规则，是一个全局自适应搜索算法，被广泛应用于函数优化、组合优化、机器学习和自动控制等领域[10].GA 的实施过程包括编解码、产生群体、计算适应度、复制、交换和变异等操作，其具体算法实现参照文献[11].

1.3 GA-BP 神经网络通风决策模型建立

传统的BP 神经网络在初始化网络权系数时一般采用的是随机给出一组初始权系数，然而BP算法所采用的是梯度下降法，对于给定的不同初始权值，往往得到的精度和稳定性是有差异的，而且不同的初始权值可能产生不同的极小值，甚至导致网络震荡，从而找不到最优解.

将GA 应用到BP 神经网络中，利用GA 的全局搜索能力，摆脱了基于梯度下降法的易陷入局部最小值的问题，并且有利于提高网络的收敛速度和泛化能力.GA 优化BP 神经网络权值和阈值的基本思想是:摒弃BP 算法利用梯度信息的指导来调整网络连接权值的方法，改用GA 直接对网络进行优化，找寻最优或近似最优的网络阈值和连接权值.

遗传-神经网络的优化问题数学描述为[12]：

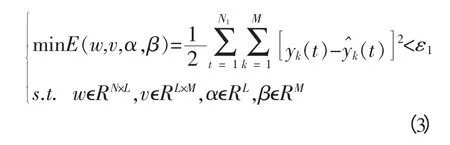
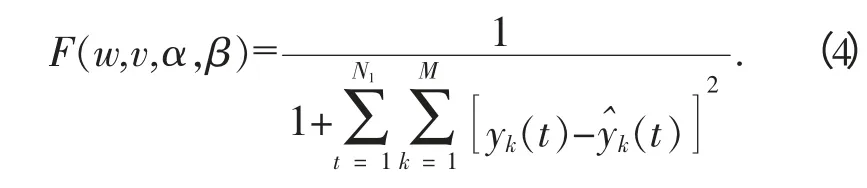
为了减少GA 的算法复杂度和网络训练时间，BP 神经网络中隐含层神经元的个数利用式（2）来确定，只利用GA 对网络的阈值和连接权值进行优化.在具体过程中，把全部样本分成训练样本集Ψ1、训练样本集Ψ2和测试样本集Φ 3 部分.具体的实现为：

（1）确定基本解空间.设定网络的训练误差，输入训练样本集Ψ1对网络进行训练，使其满足式（3），然后找出网络连接权值与阈值中的最小值和最大值分别记为umin和umax，以区间[umin-δ1，umax+δ2]（δ1，δ2为调节参数）作为连接权和阈值的基本解空间.

（2）对基本解空间编码.由于网络阈值和连接权值的学习是一个连续参数优化的复杂问题，采用二进制编码会造成码串过长，而且最终还要解码为实数，为了提高网络的学习效率和精度，直接采用实数编码.将网络的各个阈值和连接权值按输入层到隐含层的连接权w、隐含层到输出层的连接权v、隐含层阈值α 和输出层阈值β 的先后顺序连接为一个长串，构成种群的个体Pi.

（3）生成初始群体.根据确定的变量取值范围随机生成种群规模数量的个体Pi，组成初始群体.

（4）计算种群中每个个体的适应度值.将训练样本集Ψ1输入，按照式（4）定义好的适应度函数计算种群中每个个体的适应度值.

（5）遗传操作.①选择算子：为防止已搜到的最优解丢失，直接将上一代中适应度值最大的个体复制到下一代，而对其他个体采用轮盘赌法进行选取.②交叉算子：由于网络阈值和连接权采用的是实数编码，无法像二进制编码中采用等位交换的方式实施交叉操作，在这里使用整体算数交

叉实现交叉，整体算数交叉的交叉算子为[13]：

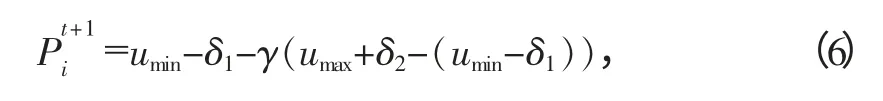
式中：Pt+1i 为父代在第i 个基因位置发生变异后产生的个体；umin，umax，δ1和δ2同步骤（1）；γ 为区间[0，1]内符合均匀分布的一个随机数.

（6）生成新一代群体.反复执行（4）（5）步，不断使种群进化，直至达到指定的进化代数.

（7）将进化产生的最后一代群体中适应度值最大的个体解码，得到相应的1 组神经网络的阈值和连接权值，将阈值和连接权值赋予网络.然后输入训练样本集Ψ2，对优化后的BP 神经网络采用BP 中的Levenberg-Marquardt（L-M）学习算法[15]对网络继续寻优.

（8）对最终得到的神经网络，利用检测样本Φ检测网络的泛化能力.

该算法采用了二次训练的方法来确定网络的阈值和连接权，充分发挥了GA 的全局搜索性能和BP 算法的局部寻优能力，克服了传统BP 神经网络的缺点，提高了网络的泛化能力.

2 试验与结果分析

2.1 确定网络结构

以山西洪洞直属库的粮仓通风来建立GA-BP神经网络粮仓通风决策模型，以记录的粮温、仓温（储粮顶部到仓顶之间的温度）、外温（外界大气的温度）、仓湿（储粮顶部到仓顶之间的湿度）和外湿（外界大气湿度）5 种特征信息组成特征向量作为输入信息，以粮仓的降温通风、降水通风和不通风3 种模式作为输出信息.根据前述理论分析，GABP 神经网络的输入层应取5 个神经元，输出层取3 个神经元.由式（2）计算可得，隐含层应取4 个神经元，则试验确定为5-4-3 结构的BP 神经网络.

2.2 处理样本

采集粮库最近两年成功通风案例的粮情数据组成试验样本集，由于温度和湿度的粮情数据是以时间为主键分别存储在不同的表中，首先需要以时间为依据作数据的关联与配准.其次，由于选取Sigmoid 函数作为神经元的激活函数，而Sigmoid函数只有在区间[-1，1]时才比较灵敏，而对于此区间外的数据变化则非常缓慢，为了加快网络的收敛速度，前期需对输入数据作预处理，使输入数据尽量位于[-1，1]区间内.对数据做预处理的另一个好处就是可以消除输入样本各元素取值范围的不一致性，减少网络优化过程的波动性，从而加速网络的训练.这里采用一种简单有效的处理方法，将数据归一化到区间[0，1]，具体处理为：以输入样本集里的样本为行向量组成一个样本矩阵，则矩阵的各列对应构成输入样本的各同质元素；找出矩阵每列的最小值和最大值；然后通过下式对数据进行处理：

其中，bij为变换后矩阵元素（实际输入特征向量元素），aij为原样本矩阵元素，aminj和amaxj分别为原样本矩阵中第j 列元素中的最大值和最小值.最后，将样本分成训练样本集Ψ1、训练样本集Ψ2和测试样本集Φ 3 组，其中，训练样本集Ψ1由降温通风、不通风和降水通风各25 组样本组成；训练样本集Ψ2由降温通风、不通风和降水通风各15 组样本组成；测试样本集Φ 由降温通风、不通风和降水通风各10 组样本组成.

2.3 输出的编码转换

为了网络的数据化处理，这里将3 种通风模式进行二进制编码映射：

2.4 参数设定及网络训练

设定GA 的初始种群S=20，进化代数K=100，交叉概率Pc=0.85，变异概率Pm=0.005，BP 的误差精度为0.000 1.按照建立模型的步骤建立GA-BP神经网络通风决策模型，将训练样本输入网络，在GA 优化网络过程中适应度函数进化曲线如图2所示；图3 为L-M 学习算法二次优化网络的收敛结果.将测试样本输入训练好的网络，该模型对测试样本集Φ 的部分通风决策结果如表1 所示.

2.5 结果分析

对于反映网络输出误差的式（4）中定义的适应度函数，从图2 中可以发现，用GA 优化网络可以在一定代数内使误差达到指定要求；从图3 可以看出，用L-M 学习算法对GA 优化过的网络进行二次优化可以在很少的步数内达到很高的误差精度，克服了传统BP 神经网络中存在的问题.另外，从表1 可以看出，作者介绍的通风决策模型具有较好的泛化能力，在实际输出和期望输出误差满足5%以内时对测试样本的模式决策和实际采取的通风模式完全符合，试验结果达到预期目标.在实际应用过程中，获取的5 种特征信息会受采集这些信息的传感器的误差和位置影响，单一的通风决策结果有时会有偏差甚至是与实际相悖的通风决策.因此，为了消除这种影响，同时考虑到粮堆内部可能出现局部聚热现象对内部传感器产生影响，可以选择靠近仓壁的传感器来抽取多组数据，组成一个测试样本集，然后用训练好的神经网络对测试样本逐一进行通风决策，最后应用统计学原理进行最终的通风模式决策.

表1 测试样本通风决策结果

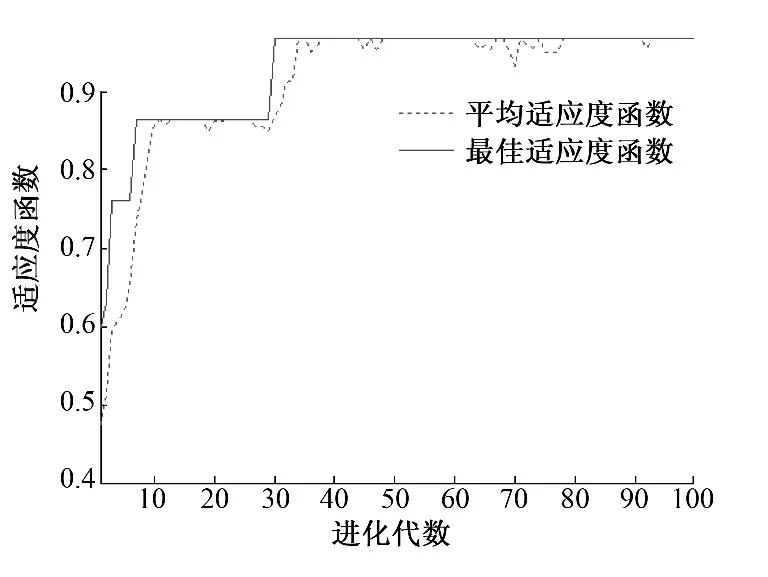
图2 适应度函数进化曲线

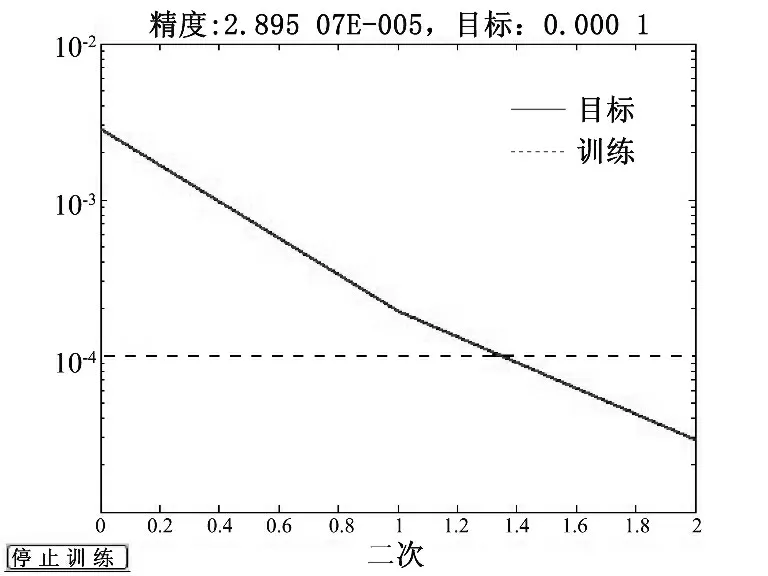
图3 L-M 学习算法二次优化网络收敛结果

3 结论

作者在剖析原有基于专家系统的粮仓通风决策存在问题的基础上，给出了一种遗传算法优化BP 神经网络并进行二次优化的GA-BP 神经网络粮仓通风决策模型.该模型有利于在实时粮情监测的环境中对通风模式进行智能决策（包括不通风模式），充分捕捉有利的通风时机，避免无效通风和有害通风等现象的发生.另外，作者所采用的建模方法充分利用了GA 的全局搜索性能力和BP神经网络的局部寻优能力，克服了传统BP 神经网络易陷入局部极小值和收敛速度慢等缺点，提高了网络的收敛速度和精度.应用该模型对山西洪洞粮库的通风决策进行试验，结果表明，该模型具有较好的泛化性能，测试样本集的通风决策结果和实际通风模式有较好的符合度，说明应用该模型进行粮仓的智能通风决策具有可行性.

［1］张来林，金文，朱庆芳，等.储粮通风技术的应用及发展［J］.粮食加工，2011，36（3）:66-70.

［2］刘卫红.基于神经网络与专家系统集成的智能决策系统的应用研究［D］.重庆:重庆大学，2002.

［3］付鹏程，赵小军，王伟，等.智能通风储粮技术在中国的发展应用概况［J］.粮食储藏，2012，41（5）:143-146.

［4］陈德发，秦维平，马飞.改进型储粮智能通风系统实仓应用效果［J］.粮油仓储科技通讯，2013，29（3）:43-45.

［5］冯黎明，陈卫东，吕宗旺，等.储粮智能通风系统研究［J］.电脑知识与技术，2013，9（15）:3588-3590.

［6］余吉庆，李宗良，周智华，等.智能通风在储粮降温中扩大应用的研究［J］.粮食储藏，2012，41（6）:22-26.

［7］黄志宏，林春华.智能化粮库建设的探讨与构想［J］.粮食储藏，2012，41（1）:52-56.

［8］Krylov N V.Introduction to the theory of random processes［M］.Providence，Rhode Island：American Mathematical Society，2002.

［9］林开平.人工神经网络的泛化性能与降水预报的应用研究［D］.南京:南京信息工程大学，2007.

［10］葛继科，邱玉辉，吴春明，等.遗传算法研究综述［J］.计算机应用研究，2008，25（10）:2911-2916.

［11］钟珞，饶文碧，邹承明.人工神经网络及其融合应用研究［M］.北京:科学出版社，2007:69-81.

［12］Hopfield J J.Neural networks and physical systems with emergent collective computation abilities［C］.Washington:Proceedings of the National Academy of Science，1982，98（11）:2554-2558.

［13］玄光男，程润伟.遗传算法与工程设计［M］.北京：科学出版社，2000:85-87.

［14］雷英杰，张善文，李续武，等.MATLAB 遗传算法工具箱及应用［M］.西安:西安电子科技大学出版社，2005:55-57.

［15］张德丰，何正风，周品，等.MATLAB 神经网络应用设计［M］.北京:机械工业出版社，2012:146-158.