基于光学相关器的光学稳像器研究

唐武盛，隋京高，张小亚，张圣辉，陈怡休，贾 辉，杨建坤

(国防科学技术大学 理学院，湖南 长沙 410073)

引言

随着对光学成像要求的提高，拍摄时相机抖动对成像质量造成的影响必须得到有效克服，因此人们提出了稳像的概念。流行当前的稳像技术大多是用电子和机械的方法实现的。美军军事研究实验室(ARL)研制的应用在无人驾驶越野车上的稳像系统，稳像速度达到30帧/s，稳像精度已优于1个像元[1]。传统电子和机械稳像技术在处理速度上存在极限，同时也由于精度不高只能应用在相机等普通器件上。基于光学相关器的稳像方法是综合较早出现的光学相关运算的概念[2]，用光学计算的方法实现稳像，摆脱传统电子与机械稳像的性能瓶颈。在国外，K. Janschek等人于2007年提出了基于联合变换相关器的适时运动补偿(即稳像)结构，在SNR较低的条件下达到了2 000次/s的相关运算速度(256像元×256像元)，其相关运算输出的RMS误差达到0.05像元[3]。在国内，中国科学院西安光学精密机械研究所于2010年提出了基于联合变换相关器的光电数字混合稳像系统的概念[4]，成为稳像器的重要理论支撑。本文以光学联合变换相关器为核心，充分发挥光学计算的速度优势，通过优化相关峰提取方法和补偿算法，大大减少了系统误差，提高了稳像器的测量精度，实现了高速视频的实时、高精度稳像。相较于前文提到的各种稳像技术，该稳像器能够进行实时处理，大大减小了亚像元误差，并在实验室条件下实现了旋转稳像。

1 基于光学相关器的稳像原理

基于光学相关器的稳像系统基本原理：通过对高速视频前后两帧图像进行光学联合相关变换(joint transform correlation，JTC)，产生相关峰，而相关峰位置信息反映了两帧图像的像移差，利用该像移差可进行图像的稳像。

1.1 用于稳像的光学相关器

光学稳像器的核心是光学联合变换相关器[5]，简称光学相关器，它可以通过高速视频流前后两帧的对比，探测出两帧图像的微小像移差。光学联合变换器一般采用4-f系统，其原理如图1所示。图1中，P1、P2、P3分别是物平面、谱平面和像平面，它们和2个傅里叶透镜L1、L2的距离均为焦距f。参考图像和目标图像中心相距2b，经过2个透镜傅里叶变换后，相关峰距离4b。

图1 联合变换相关器原理Fig.1 Principle of joint transform correlation

为实现稳像功能，对图1光路进行重新设计，达到进一步缩小尺寸及小型化要求，采用如图2(a)所示的折叠光路，实现相关处理。上述光路中，核心器件是基于反射式数字微镜元件(digital mirror device，DMD)的空间光调制器(spatial light modulator，SLM)，速率可达10 000帧/s，能够满足实时性要求。DMD按时序控制依次显示拼接视频(连续两帧分别作为参考图像和目标图像)和频谱图，频谱图再次经过傅里叶透镜(L2)，得到相关峰图像，由高速CCD(每秒千帧图像探测)接收。用来加载图像的激光由氦氖激光器提供，准直扩束系统(L1)和全内反射棱镜(TIR)是为了保证激光到DMD的入射角度而设计。图2(a)中，光学相关器的3个主要部件DMD、傅里叶透镜(L2)、CCD都被复用，系统大大缩小了稳像器的体积，实物如图2(b)。

图2 光学稳像器结构示意图Fig.2 Optical image stabilization layout

1.2 像移差的产生及补偿

对平移稳像来说[6]，取DMD中心为坐标原点，以当前帧f0(x,y)作为参考图像，下一帧f1(x,y)作为对比图像，横向拼接后对称地输入DMD，输入坐标为(x0,0)和(-x0,0)，则当前帧为f0(x+x0,y)。假设下一帧相对当前帧有(Δx1,Δy1)的位移矢量，则表示为f1(x-x0-Δx1,y-Δy1)。输入面就有以下形式:

f(x,y)=f0(x+x0,y)+f1(x-x0-Δx1,

y-Δy1)

(1)

该面经过傅里叶透镜，在CCD处得到f(x,y)的频谱图为

(2)

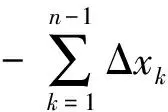
就旋转稳像来说，其核心仍旧是对参考帧和对比帧进行光学联合相关变换，只是在补偿算法上，与平移稳像有所不同。取当前帧f0(x,y)作为参考图像，下一帧f1(x,y)作为对比图像。假设下一帧f1(x,y)是参考帧f0(x,y)逆时针旋转Δθ1得到的图像，则两者之间在理论上满足[5]：

f1(x,y)=f0(xcosΔ1+ysinΔθ1,-xsinΔθ1+

ycosΔθ1)

(3)

通过水平和垂直方向上的位移差得到旋转角度Δθ1。同样的方法依次得到每帧图像之间的Δθk，补偿之后完成旋转稳像。

1.3 稳像原理

综合上述过程，运用光学稳像器能够探测出一系列像移差，在系统的一次曝光周期内，根据这些像移差组成的累计运动矢量对每一帧都进行运动补偿，其技术原理如图3所示。

图3 光学稳像器技术原理示意图Fig.3 Principle diagram of optical image stabilization technology

连续2次傅里叶变换能够得到相关峰位置变化信息，提取出像移差反馈给计算机，补偿输出稳定视频流。

2 稳像实验

为提高稳像精度，减小系统误差和相关峰位置提取亚像元误差，对相关峰位置提取算法和图像补偿算法进行优化，并利用光学计算的速度优势完成了旋转稳像的实验。

2.1 实验过程

按照光学稳像器的原理要求，利用前端相机随机采集了景物视频流图像，将其输入计算机进行预处理。采用Labview软件将视频第一帧与第二帧拼接后输入DMD，如图4(a)所示。输入图像经过第一次傅里叶变换后，在CCD上得到两幅图像的联合频谱图，再经过第二次傅里叶变换，产生相关峰输出，如图4(b)所示。当输入的图像稳定时，相关峰的相对位置不变。某一时刻引入不规则抖动时，图像因为相机的平移产生像移。相关峰的位置随之改变，与起始坐标产生差值。采用软件进行实时补偿，输出处理后的稳定图像。

图4 实验中计算机显示内容Fig.4 Image displaying on computer

实验中计算机实时显示预处理后相邻两帧的拼接图像(分辨率1 024像元×768像元)。每一次光学处理后，均会得到频谱图以及相关峰的坐标信息。待稳视频和经过光学稳像器处理后的稳定视频同时显示在屏幕上，可以动态地观察稳像效果。如图5所示，待稳视频中的某一帧图像经过光学稳像器后得到稳定图像。

图5 稳像前后视频图像效果对比Fig.5 Before and after video image stabilization

2.2 相关峰位置提取及亚像元误差分析

在稳像过程中，稳像器在补偿一定数量的单帧图像后，产生固定的补偿误差。为得到稳像误差，用一个特定目标(本文采用黑色圆)的可控运动来模拟相机的运动。保持前后两幅图像在DMD上相对位置不变，使用2种不同口径(25 mm和80 mm)傅立叶透镜，得到的误差波动范围分别约为0.2像元和0.1个像元。目标图像在DMD的不同位置对应于目标在进行光学傅里叶变换时的不同入射角，经光学稳像器计算后，得到相关峰位置的波动。然后，利用二次加权质心提取算法[7]得到相关峰位置变化值。经过分析，本系统主要误差应该是由傅里叶透镜的像差以及算法累积误差引起。如图6(a)所示。为检验亚像元提取误差对结果的影响，实验中采用固定DMD中的一个目标，另一个目标每20帧移动1个像元进行匀速运动。处理后得到相关峰位置信息随运动目标图像的变化关系，如图6(b)所示的实线。利用最小二乘法的原理，用一条斜直线拟合，得到相关峰位置真值，如图6(b)所示的虚线。

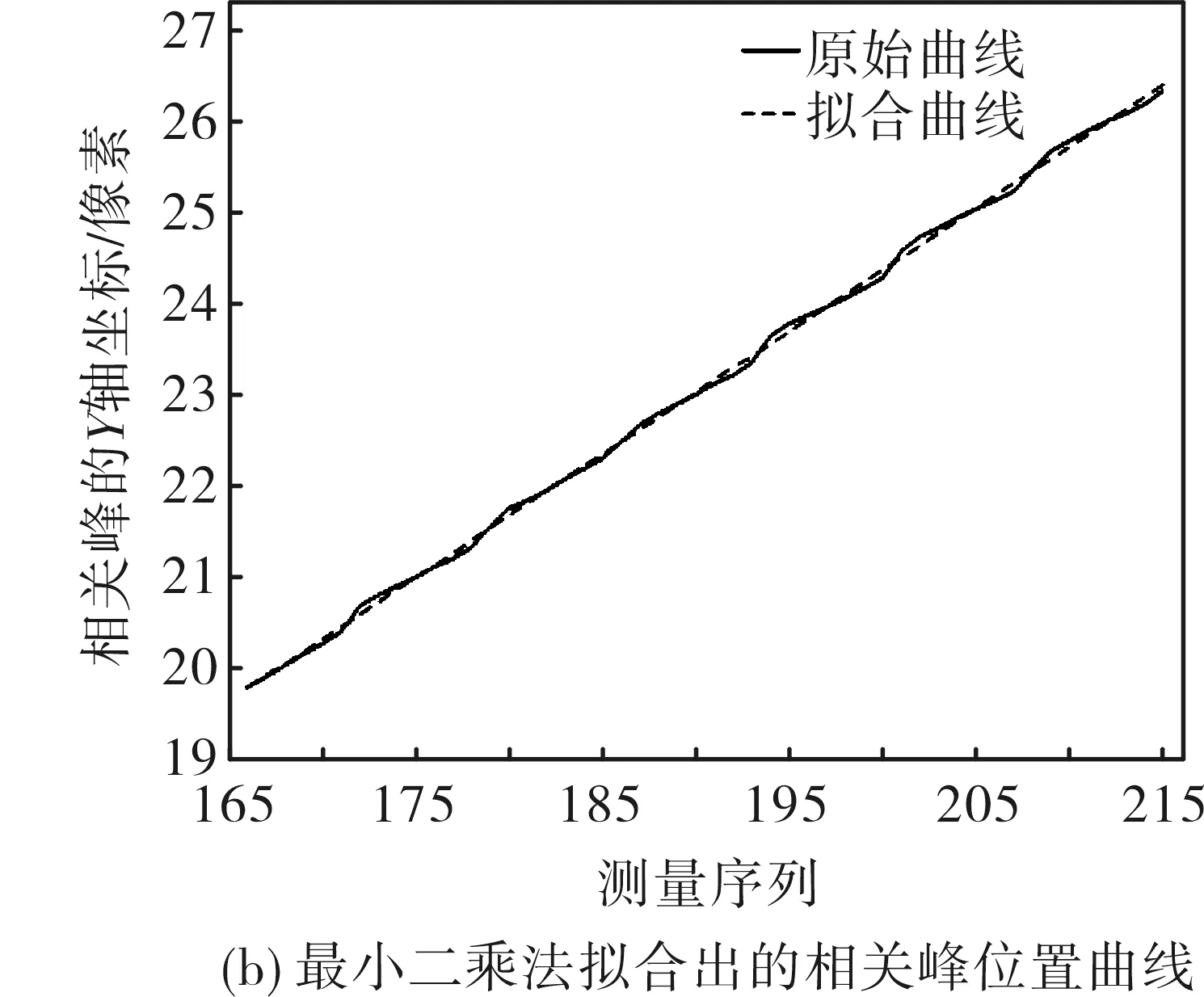
图6 提取相关峰坐标Fig.6 Extracting coordinates of correlation peak

对比发现，相关峰位置仿真实验值和真值之间存在明显的亚像元误差。通过对算法进行优化，采用多次加权平均方法，得到相关峰位置提取的最佳算法[7]。根据残差理论[8]，在相关实验基础上得到图7所示的补偿后的残差图，可看出这种补偿方法可将亚像元误差的残差波动范围从约±0.1个像元补偿到约±0.04个像元，大大减小了亚像元误差，有效提高了坐标位置的提取精度。

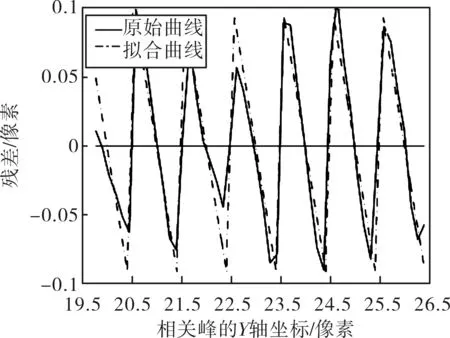
图7 残差与质心坐标关系Fig.7 Relation between residual error and facula centroid coordinate

2.3 旋转条件下的稳像

在旋转条件下，将视频流相邻两帧拼接后输入到DMD上，经过光学相关器的计算，得到输入图像频谱图的相关峰图像，如图8所示。提取相关峰坐标，可以计算出旋转的角度为Δθ1。

图8 目标图像旋转前后相关峰图像Fig.8 Images of correlation peak before and after rotation

将第二帧图像逆时针旋转Δθ1后输出，两帧图像间没有位矢差。对其余图像依次进行相同过程，得到稳定的视频流图像，如图9所示。

图9 旋转稳像前后视频图像对比Fig.9 Before and after video image stabilization of rotation

两帧的差异还体现在尺度上的变化[9]，由于光学相关处理能够识别图像很小的旋转角，在这种条件下，可以认为两帧图像在尺度上保持不变。构建旋转与平移关系的算法[10]，就能够得到需要补偿的旋转角。取实际拍摄景物进行对比，得到光学稳像器能够进行稳像的最小旋转角度低至0.1°。

3 结论

本文在阐明光学相关稳像器原理的基础上，设计方案进行了实验，实现了光学稳像器的功能。对于实验过程中出现的系统误差和亚像元误差，通过亚像元定位补偿，使得实验误差达到最小。在实验室条件下，实现了高速视频的抖动和旋转稳像。实验表明，稳像器平移稳像的精度可以达到±0.1个像元(改进补偿算法后可达±0.04个像元)，旋转稳像的精度可达0.1°。

在实验中，由于器件对图像的要求较高，待稳视频在进入光学系统前必须进行预处理，降低了整个系统的处理速度；对DMD进行复用时，时序控制尤其重要，偶尔会出现乱帧现象；对于稍大角度的旋转，光学相关器就会误认为是相机的正常旋转，不对图像进行稳像，低于预期效果。通过算法改进、视频流控制，光路调整等措施，基于光学相关器的光学稳像器会继续向集成化，小型化发展，大大提高了实用性。

[1] Han Shaokun, Zhao Yuejin, Liu Mingqi, et al. Electronic image stabilization techniques and development[J]. Optical Technique, 2001,7(1):71-73.

韩绍坤,赵跃进,刘明奇,等. 电子稳像技术及其发展[J]. 光学技术,2001,7(1):71-73.

[2] Goodman J W. Introduction to Fourier optics[M]. New York: Mc-Graw-Hill,1968.

[3] Janschek K, Tchernykh V, Dyblenko S. Performance analysis of opto-mechatronic image stabilization for a compact space camera[J]. Control Engineering Practice, 2007, 15(3): 333-347.

[4] Yi Hongwei, Zhao Hui, Wen Desheng, et al. Static simulation experiment of image motion measurement based on optical joint transform correlator[J]. Acta Optica Sinica, 2010, 30(12):3471-3475.

易红伟,赵惠,汶德胜,等. 联合变换相关器像移测量静态仿真实验分析[J]. 光学学报, 2010, 30(12):3471-3475.

[5] Ma Jin, Tian Tao. Target tracking method based on joint transform correlation[J]. Journal of Applied Optics,2012,33(5):904-908.

马进,田涛.基于联合变换相关的目标跟踪方法[J].应用光学,2012,33(5): 904-908.

[6] Yi Hongwei, Zhao Hui, Li Yingcai, et al. Improved digital processing method used for image motion measurement based on hybrid opto-digital joint transform correlator[J]. Chinese Optics Letters, 2010, 8(10):989-992.

[7] Zhang Xiaoya, Sui Jinggao, Tang Wusheng, et al. Subpixel centroid error analysis and compensation for optical joint transform correlator[J]. Chinese Journal of Lasers, 2012, 39(s2): s209006.

张小亚,隋京高,唐武盛,等. 光学联合变换相关器相关峰亚像素定位误差的分析与补偿[J]. 中国激光, 2012, 39(s2): s209006.

[8] Song Feijun,Jutamulia S.Modern optical information processing[M]. Beijing: Beijing University Press, 200,78-84.

宋菲君, S.Jutamulia.近代光学信息处理[M].北京：北京大学出版社，2001:78-84.

[9] Du Dengchong, Jiang Xiaoyu, Yao Jun. Electronic image stabilization algorithm for estimating rotation and translation simultaneously[J]. Computer Engineering and Application, 2010,46(4):233-235.

杜登崇,蒋晓瑜,姚军.可同时估计旋转和平移的电子稳像方法[J]. 计算机工程与应用, 2010,46(4):233-235.

[10] Mao Liangjin. Research and implementation of rotating electronic image stabilization technology[D]. Hangzhou: Zhejiang University, 2010.

毛良瑾. 旋转电子稳像技术的研究和实现[D]. 杭州: 浙江大学，2010.